第十七章排序 · 數據結構思維中文版

# 第十七章排序 > 原文：[Chapter 17 Sorting](http://greenteapress.com/thinkdast/html/thinkdast018.html) > 譯者：[飛龍](https://github.com/wizardforcel) > 協議：[CC BY-NC-SA 4.0](http://creativecommons.org/licenses/by-nc-sa/4.0/) > 自豪地采用[谷歌翻譯](https://translate.google.cn/) 計算機科學領域過度癡迷于排序算法。根據 CS 學生在這個主題上花費的時間，你會認為排序算法的選擇是現代軟件工程的基石。當然，現實是，軟件開發人員可以在很多年中，或者整個職業生涯中，不必考慮排序如何工作。對于幾乎所有的應用程序，它們都使用它們使用的語言或庫提供的通用算法。通常這樣就行了。所以如果你跳過這一章，不了解排序算法，你仍然是一個優秀的開發人員。但是有一些原因你可能想要這樣： + 盡管有絕大多數應用程序都可以使用通用算法，但你可能需要了解兩種專用算法：基數排序和有界堆排序。 + 一種排序算法，歸并排序，是一個很好的教學示例，因為它演示了一個重要和實用的算法設計策略，稱為“分治”。此外，當我們分析其表現時，你將了解到我們以前沒有看到的增長級別，即線性對數。最后，一些最廣泛使用的算法是包含歸并排序的混合體。 + 了解排序算法的另一個原因是，技術面試官喜歡詢問它們。如果你想要工作，如果你能展示 CS 文化素養，就有幫助。因此，在本章中我們將分析插入排序，你將實現歸并排序，我將給你講解基數排序，你將編寫有界堆排序的簡單版本。 ## 17.1 插入排序我們將從插入排序開始，主要是因為它的描述和實現很簡單。它不是很有效，但它有一些補救的特性，我們將看到它。我們不在這里解釋算法，建議你閱讀 <http://thinkdast.com/insertsort> 中的插入排序的維基百科頁面，其中包括偽代碼和動畫示例。當你理解了它的思路再回來。這是 Java 中插入排序的實現： ```java public class ListSorter<T> { public void insertionSort(List<T> list, Comparator<T> comparator) { for (int i=1; i < list.size(); i++) { T elt_i = list.get(i); int j = i; while (j > 0) { T elt_j = list.get(j-1); if (comparator.compare(elt_i, elt_j) >= 0) { break; } list.set(j, elt_j); j--; } list.set(j, elt_i); } } } ``` 我定義了一個類，`ListSorter`作為排序算法的容器。通過使用類型參數`T`，我們可以編寫一個方法，它在包含任何對象類型的列表上工作。 `insertionSort`需要兩個參數，一個是任何類型的`List`，一個是`Comparator`，它知道如何比較類型`T`的對象。它對列表“原地”排序，這意味著它修改現有列表，不必分配任何新空間。下面的示例演示了，如何使用`Integer`的`List`對象，調用此方法： ```java List<Integer> list = new ArrayList<Integer>( Arrays.asList(3, 5, 1, 4, 2)); Comparator<Integer> comparator = new Comparator<Integer>() { @Override public int compare(Integer elt1, Integer elt2) { return elt1.compareTo(elt2); } }; ListSorter<Integer> sorter = new ListSorter<Integer>(); sorter.insertionSort(list, comparator); System.out.println(list); ``` `insertionSort`有兩個嵌套循環，所以你可能會猜到，它的運行時間是二次的。在這種情況下，一般是正確的，但你做出這個結論之前，你必須檢查，每個循環的運行次數與`n`，數組的大小成正比。外部循環從`1`迭代到`list.size()`，因此對于列表的大小`n`是線性的。內循環從`i`迭代到`0`，所以在`n`中也是線性的。因此，兩個循環運行的總次數是二次的。如果你不確定，這里是證明：第一次循環中，`i = 1`，內循環最多運行一次。第二次，`i = 2`，內循環最多運行兩次。最后一次，`i = n - 1`，內循環最多運行`n`次。因此，內循環運行的總次數是序列`1, 2, ..., n - 1`的和，即`n(n - 1)/2`。該表達式的主項（擁有最高指數）為`n^2`。在最壞的情況下，插入排序是二次的。然而： + 如果這些元素已經有序，或者幾乎這樣，插入排序是線性的。具體來說，如果每個元素距離它的有序位置不超過`k`個元素，則內部循環不會運行超過`k`次，并且總運行時間是`O(kn)`。 + 由于實現簡單，開銷較低；也就是，盡管運行時間是`an^2`，主項的系數`a`，也可能是小的。所以如果我們知道數組幾乎是有序的，或者不是很大，插入排序可能是一個不錯的選擇。但是對于大數組，我們可以做得更好。其實要好很多。 ## 17.2 練習 14 歸并排序是運行時間優于二次的幾種算法之一。同樣，不在這里解釋算法，我建議你閱讀維基百科 <http://thinkdast.com/mergesort>。一旦你有了想法，反回來，你可以通過寫一個實現來測試你的理解。在本書的倉庫中，你將找到此練習的源文件： + `ListSorter.java` + `ListSorterTest.java` 運行`ant build`來編譯源文件，然后運行`ant ListSorterTest`。像往常一樣，它應該失敗，因為你有工作要做。在`ListSorter.java`中，我提供了兩個方法的大綱，`mergeSortInPlace`以及`mergeSort`： ```java public void mergeSortInPlace(List<T> list, Comparator<T> comparator) { List<T> sorted = mergeSortHelper(list, comparator); list.clear(); list.addAll(sorted); } private List<T> mergeSort(List<T> list, Comparator<T> comparator) { // TODO: fill this in! return null; } ``` 這兩種方法做同樣的事情，但提供不同的接口。`mergeSort`獲取一個列表，并返回一個新列表，具有升序排列的相同元素。`mergeSortInPlace`是修改現有列表的`void`方法。你的工作是填充`mergeSort`。在編寫完全遞歸版本的合并排序之前，首先要這樣： + 將列表分成兩半。 + 使用`Collections.sort`或`insertionSort`來排序這兩部分。 + 將有序的兩部分合并為一個完整的有序列表中。這將給你一個機會來調試用于合并的代碼，而無需處理遞歸方法的復雜性。接下來，添加一個邊界情況（請參閱 < http://thinkdast.com/basecase> ）。如果你只提供一個列表，僅包含一個元素，則可以立即返回，因為它已經有序。或者如果列表的長度低于某個閾值，則可以使用`Collections.sort`或`insertionSort`。在進行前測試邊界情況。最后，修改你的解決方案，使其進行兩次遞歸調用來排序數組的兩個部分。當你使其正常工作，`testMergeSort`和`testMergeSortInPlace`應該通過。 ## 17.3 歸并排序的分析為了對歸并排序的運行時間進行劃分，對遞歸層級和每個層級上完成多少工作方面進行思考，是很有幫助的。假設我們從包含`n`個元素的列表開始。以下是算法的步驟： + 生成兩個新數組，并將一半元素復制到每個數組中。 + 排序兩個數組。 + 合并兩個數組。圖 17.1 顯示了這些步驟。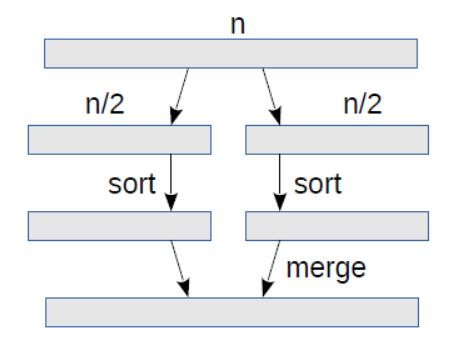 ![](https://img.kancloud.cn/69/ad/69adcb6b13990685b8c89dc1d50ba82a_458x352.jpg) 圖 17.1：歸并排序的展示，它展示了遞歸的一個層級。第一步復制每個元素一次，因此它是線性的。第三步也復制每個元素一次，因此它也是線性的。現在我們需要弄清楚步驟`2`的復雜性。為了做到這一點，查看不同的計算圖片會有幫助，它展示了遞歸的層數，如圖 17.2 所示。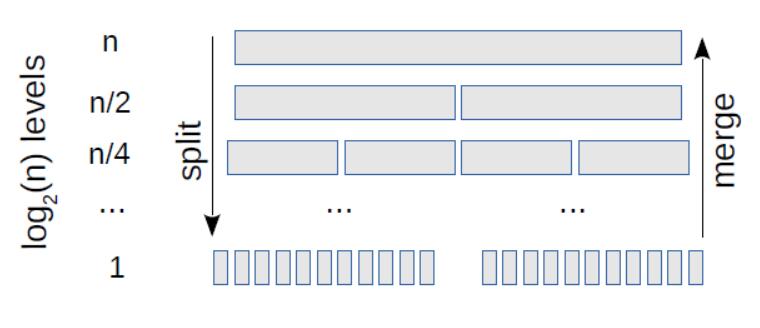 ![](https://img.kancloud.cn/a8/65/a865e22ed0734a2a9cc0430809ae046f_760x328.jpg) 圖 17.2：歸并排序的展示，它展示了遞歸的所有層級。在頂層，我們有`1`個列表，其中包含`n`個元素。為了簡單起見，我們假設`n`是`2`的冪。在下一層，有`2`個列表包含`n/2`個元素。然后是`4`個列表與`n/4`元素，以此類推，直到我們得到`n`個列表與`1`元素。在每一層，我們共有`n`個元素。在下降的過程中，我們必須將數組分成兩半，這在每一層上都需要與`n`成正比的時間。在回來的路上，我們必須合并`n`個元素，這也是線性的。如果層數為`h`，算法的總工作量為`O(nh)`。那么有多少層呢？有兩種方法可以考慮： + 我們用多少步，可以將`n`減半直到`1`？ + 或者，我們用多少步，可以將`1`加倍直到`n`？第二個問題的另一種形式是“`2`的多少次方是`n`”？ ``` 2^h = n ``` 對兩邊取以`2`為底的對數： ``` h = log2(n) ``` 所以總時間是`O(nlogn)`。我沒有糾結于對數的底，因為底不同的對數差別在于一個常數，所以所有的對數都是相同的增長級別。 `O(nlogn)`中的算法有時被稱為“線性對數”的，但大多數人只是說`n log n`。事實證明，`O(nlogn)`是通過元素比較的排序算法的理論下限。這意味著沒有任何“比較排序”的增長級別比`n log n`好。請參見 <http://thinkdast.com/compsort>。但是我們將在下一節中看到，存在線性時間的非比較排序！ ## 基數排序在 2008 年美國總統競選期間，候選人巴拉克·奧巴馬在訪問 Google 時，被要求進行即興算法分析。首席執行長埃里克·施密特開玩笑地問他，“排序一百萬個 32 位整數的最有效的方法”。顯然有人暗中告訴了奧巴馬，因為他很快就回答說：“我認為冒泡排序是錯誤的。”你可以在 <http://thinkdast.com/obama> 觀看視頻。奧巴馬是對的：冒泡排序在概念上是簡單的，但其運行時間是二次的; 即使在二次排序算法中，其性能也不是很好。見 <http://thinkdast.com/bubble>。施密特想要的答案可能是“基數排序”，這是一種非比較排序算法，如果元素的大小是有界的，例如 32 位整數或 20 個字符的字符串，它就可以工作。為了看看它是如何工作的，想象你有一堆索引卡，每張卡片包含三個字母的單詞。以下是一個方法，可以對卡進行排序： + 根據第一個字母，將卡片放入桶中。所以以`a`開頭的單詞應該在一個桶中，其次是以`b`開頭的單詞，以此類推 + 根據第二個字母再次將卡片放入每個桶。所以以`aa`開頭的應該在一起，其次是以`ab`開頭的，以此類推當然，并不是所有的桶都是滿的，但是沒關系。 + 根據第三個字母再次將卡片放入每個桶。此時，每個桶包含一個元素，桶按升序排列。圖 17.3 展示了三個字母的例子。 ![](https://img.kancloud.cn/5a/c1/5ac10b115cc35dd8952f2955c56ff974_780x284.jpg) 圖 17.3：三個字母的基數排序的例子最上面那行顯示未排序的單詞。第二行顯示第一次遍歷后的桶的樣子。每個桶中的單詞都以相同的字母開頭。第二遍之后，每個桶中的單詞以相同的兩個字母開頭。在第三遍之后，每個桶中只能有一個單詞，并且桶是有序的。在每次遍歷期間，我們遍歷元素并將它們添加到桶中。只要桶允許在恒定時間內添加元素，每次遍歷是線性的。遍歷數量，我會稱之為`w`，取決于單詞的“寬度”，但不取決于單詞的數量，`n`。所以增長級別是`O(wn)`，對于`n`是線性的。基數排序有許多變體，并有許多方法來實現每一個。你可以在 <http://thinkdast.com/radix> 上閱讀他們的更多信息。作為一個可選的練習，請考慮編寫基數排序的一個版本。 ## 17.5 堆排序基數排序適用于大小有界的東西，除了他之外，還有一種你可能遇到的其它專用排序算法：有界堆排序。如果你在處理非常大的數據集，你想要得到前 10 個或者前`k`個元素，其中`k`遠小于`n`，它是很有用的。例如，假設你正在監視一個Web 服務，它每天處理十億次事務。在每一天結束時，你要匯報最大的`k`個事務（或最慢的，或者其它最 xx 的）。一個選項是存儲所有事務，在一天結束時對它們進行排序，然后選擇最大的`k`個。需要的時間與`nlogn`成正比，這非常慢，因為我們可能無法將十億次交易記錄在單個程序的內存中。我們必須使用“外部”排序算法。你可以在 <http://thinkdast.com/extsort> 上了解外部排序。使用有界堆，我們可以做得更好！以下是我們的實現方式： + 我會解釋（無界）堆排序。 + 你會實現它 + 我將解釋有界堆排序并進行分析。要了解堆排序，你必須了解堆，這是一個類似于二叉搜索樹（BST）的數據結構。有一些區別： + 在 BST 中，每個節點`x`都有“BST 特性”：`x`左子樹中的所有節點都小于`x`，右子樹中的所有節點都大于`x`。 + 在堆中，每個節點`x`都有“堆特性”：兩個子樹中的所有節點都大于`x`。 + 堆就像平衡的 BST；當你添加或刪除元素時，他們會做一些額外的工作來重新使樹平衡。因此，可以使用元素的數組來有效地實現它們。 > 譯者注：這里先討論最小堆。如果子樹中所有節點都小于`x`，那么就是最大堆。堆中最小的元素總是在根節點，所以我們可以在常數時間內找到它。在堆中添加和刪除元素需要的時間與樹的高度`h`成正比。而且由于堆總是平衡的，所以`h`與`log n`成正比。你可以在 <http://thinkdast.com/heap> 上閱讀更多堆的信息。 Java`PriorityQueue`使用堆實現。`PriorityQueue`提供`Queue`接口中指定的方法，包括`offer`和`poll`： + `offer`：將一個元素添加到隊列中，更新堆，使每個節點都具有“堆特性”。需要`logn`的時間。 + `poll`：從根節點中刪除隊列中的最小元素，并更新堆。需要`logn`的時間。給定一個`PriorityQueue`，你可以像這樣輕松地排序的`n`個元素的集合： + 使用`offer`，將集合的所有元素添加到`PriorityQueue`。 + 使用`poll`從隊列中刪除元素并將其添加到`List`。因為`poll`返回隊列中剩余的最小元素，所以元素按升序添加到`List`。這種排序方式稱為堆排序（請參閱 <http://thinkdast.com/heapsort>）。向隊列中添加`n`個元素需要`nlogn`的時間。刪除`n`個元素也是如此。所以堆排序的運行時間是`O(n logn)`。在本書的倉庫中，你可以在`ListSorter.java`中找到`heapSort`方法的大綱。填充它，然后運行`ant ListSorterTest`來確認它可以工作。 ## 17.6 有界堆排序有界堆是一個限制為最多包含`k`個元素的堆。如果你有`n`個元素，你可以跟蹤這個最大的`k`個元素：最初堆是空的。對于每個元素`x`： + 分支 1：如果堆不滿，請添加`x`到堆中。 + 分支 2：如果堆滿了，請與堆中`x`的最小元素進行比較。如果`x`較小，它不能是最大的`k`個元素之一，所以你可以丟棄它。 + 分支 3：如果堆滿了，并且`x`大于堆中的最小元素，請從堆中刪除最小的元素并添加`x`。使用頂部為最小元素的堆，我們可以跟蹤最大的`k`個元素。我們來分析這個算法的性能。對于每個元素，我們執行以下操作之一： + 分支 1：將元素添加到堆是`O(log k)`。 + 分支 2：找到堆中最小的元素是`O(1)`。 + 分支 3：刪除最小元素是`O(log k)`。添加`x`也是`O(log k)`。在最壞的情況下，如果元素按升序出現，我們總是執行分支 3。在這種情況下，處理`n`個元素的總時間是`O(n log k)`，對于`n`是線性的。在`ListSorter.java`中，你會發現一個叫做`topK`的方法的大綱，它接受一個`List`、`Comparator`和一個整數`k`。它應該按升序返回`List`的`k`個最大的元素。填充它，然后運行`ant ListSorterTest`來確認它可以工作。 ## 17.7 空間復雜性到目前為止，我們已經談到了很多運行時間的分析，但是對于許多算法，我們也關心空間。例如，歸并排序的一個缺點是它會復制數據。在我們的實現中，它分配的空間總量是`O(n log n)`。通過更機智的實現，你可以將空間要求降至`O(n)`。相比之下，插入排序不會復制數據，因為它會原地排序元素。它使用臨時變量來一次性比較兩個元素，并使用一些其它局部變量。但它的空間使用不取決于`n`。我們的堆排序實現創建了新`PriorityQueue`，來存儲元素，所以空間是`O(n)`; 但是如果你能夠原地對列表排序，則可以使用`O(1)`的空間執行堆排序。剛剛實現的有界堆棧算法的一個好處是，它只需要與`k`成正比的空間（我們要保留的元素的數量），而`k`通常比`n`小得多。軟件開發人員往往比空間更加注重運行時間，對于許多應用程序來說，這是適當的。但是對于大型數據集，空間可能同等或更加重要。例如： + 如果一個數據集不能放入一個程序的內存，那么運行時間通常會大大增加，或者根本不能運行。如果你選擇一個需要較少空間的算法，并且這樣可以將計算放入內存中，則可能會運行得更快。同樣，使用較少空間的程序，可能會更好地利用 CPU 緩存并運行速度更快（請參閱 <http://thinkdast.com/cache>）。 + 在同時運行多個程序的服務器上，如果可以減少每個程序所需的空間，則可以在同一臺服務器上運行更多程序，從而降低硬件和能源成本。所以這些是一些原因，你應該至少了解一些算法的空間需求。