# 第四章 `LinkedList` > 原文：[Chapter 4 LinkedList](http://greenteapress.com/thinkdast/html/thinkdast005.html) > 譯者：[飛龍](https://github.com/wizardforcel) > 協議：[CC BY-NC-SA 4.0](http://creativecommons.org/licenses/by-nc-sa/4.0/) > 自豪地采用[谷歌翻譯](https://translate.google.cn/) 這一章展示了上一個練習的解法，并繼續討論算法分析。 ## 4.1 `MyLinkedList`方法的劃分 我的`indexOf`實現在下面。在閱讀說明之前，請閱讀它，看看你是否可以確定其增長級別。 ```java public int indexOf(Object target) { Node node = head; for (int i=0; i<size; i++) { if (equals(target, node.data)) { return i; } node = node.next; } return -1; } ``` 最初`node`為`head`的副本，所以他們都指向相同的`Node`。循環變量`i`從`0`計數到`size-1`。每次在循環中，我們都用`equals`來看看我們是否找到了目標。如果是這樣，我們立即返回`i`。否則我們移動到列表中的下一個`Node`。 通常我們會檢查以確保下一個`Node`不是`null`，但在這里，它是安全的，因為當我們到達列表的末尾時循環結束（假設與列表中`size`與實際節點數量一致）。 如果我們走完了循環而沒有找到目標，我們返回`-1`。 那么這種方法的增長級別是什么？ + 每次在循環中，我們調用了`equals`，這是一個常數時間（它可能取決于`target`或`data`大小，但不取決于列表的大小）。循環中的其他操作也是常數時間。 + 循環可能運行`n`次，因為在更糟的情況下，我們可能必須遍歷整個列表。 所以這個方法的運行時間與列表的長度成正比。 接下來，這里是我的雙參數`add`方法的實現。同樣，你應該嘗試對其進行劃分，然后再閱讀說明。 ```java public void add(int index, E element) { if (index == 0) { head = new Node(element, head); } else { Node node = getNode(index-1); node.next = new Node(element, node.next); } size++; } ``` 如果`index==0`，我們在開始添加新的`Node`，所以我們把它當作特殊情況。否則，我們必須遍歷列表來查找`index-1`處的元素。我們使用輔助方法`getNode`： ```java private Node getNode(int index) { if (index < 0 || index >= size) { throw new IndexOutOfBoundsException(); } Node node = head; for (int i=0; i<index; i++) { node = node.next; } return node; } ``` `getNode`檢查`index`是否超出范圍；如果是這樣，它會拋出異常。否則，它遍歷列表并返回所請求的節點。 我們回到`add`，一旦我們找到合適的`Node`，我創建新的`Node`，并把它插到`node`和`node.next`之間。你可能會發現，繪制此操作的圖表有助于確保你了解此操作。 那么，`add`的增長級別什么呢？ + `getNode`類似`indexOf`，出于同樣的原因也是線性的。 + 在`add`中，`getNode`前后的一切都是常數時間。 所以放在一起，`add`是線性的。 最后，我們來看看`remove`： ```java public E remove(int index) { E element = get(index); if (index == 0) { head = head.next; } else { Node node = getNode(index-1); node.next = node.next.next; } size--; return element; } ``` `remove`使用了`get`查找和存儲`index`處的元素。然后它刪除包含它的`Node`。 如果`index==0`，我們再次處理這個特殊情況。否則我們找到節點`index-1`并進行修改，來跳過`node.next`并直接鏈接到`node.next.next`。這有效地從列表中刪除`node.next`，它可以被垃圾回收。 最后，我們減少`size`并返回我們在開始時檢索的元素。 那么，`remove`的增長級別是什么呢？`remove`中的一切是常數時間，除了`get`和`getNode`，它們是線性的。因此，`remove`是線性的。 當人們看到兩個線性操作時，他們有時會認為結果是平方的，但是只有一個操作嵌套在另一個操作中才適用。如果你在一個操作之后調用另一個，運行時間會相加。如果它們都是`O(n)`的，則總和也是`O(n)`的。 ## 4.2 `MyArrayList`和`MyLinkedList`的對比 下表總結了`MyArrayList`和`MyLinkedList`之間的差異，其中`1`表示`O(1)`或常數時間，和`n`表示`O(n)`或線性。 | | `MyArrayList` | `MyLinkedList` | | --- | --- | --- | | `add`（末尾） | 1 | n | | `add`（開頭） | n | 1 | | `add`（一般） | n | n | | `get` / `set` | 1 | n | | `indexOf` / `lastIndexOf` | n | n | | `isEmpty` / `size` | 1 | 1 | | `remove`（末尾） | 1 | n | | `remove`（開頭） | n | 1 | | `remove`（一般） | n | n | + `MyArrayList`的優勢操作是，插入末尾，移除末尾，獲取和設置。 + `MyLinkedList`的優勢操作是，插入開頭，以及移動開頭。 對于其他操作，這兩個實現方式的增長級別相同。 哪個實現更好？這取決于你最有可能使用哪些操作。這就是為什么 Java 提供了多個實現，因為它取決于你。 ## 4.3 性能分析 對于下一個練習，我提供了一個`Profiler`類，它包含代碼，使用一系列問題規模運行方法，測量運行時間和繪制結果。 你將使用`Profiler`，為 Java 的實現`ArrayList`和`LinkedList`，劃分`add`方法的性能。 以下是一個示例，展示了如何使用分析器： ```java public static void profileArrayListAddEnd() { Timeable timeable = new Timeable() { List<String> list; public void setup(int n) { list = new ArrayList<String>(); } public void timeMe(int n) { for (int i=0; i<n; i++) { list.add("a string"); } } }; String title = "ArrayList add end"; Profiler profiler = new Profiler(title, timeable); int startN = 4000; int endMillis = 1000; XYSeries series = profiler.timingLoop(startN, endMillis); profiler.plotResults(series); } ``` 此方法測量在`ArrayList`上運行`add`所需的時間，它向末尾添加新元素。我將解釋代碼，然后展示結果。 為了使用`Profiler`，我們需要創建一個`Timeable`，它提供兩個方法：`setup`和`timeMe`。`setup`方法執行在啟動計時之前所需的任何工作；這里它會創建一個空列表。然后`timeMe`執行我們試圖測量的任何操作；這里它將`n`個元素添加到列表中。 創建`timeable`的代碼是一個匿名類，用于定義`Timeable`接口的新實現，并同時創建新類的實例。如果你不熟悉匿名類，你可以閱讀這里：<http://thinkdast.com/anonclass>。 但是下一次練習不需要太多的知識；即使你不喜歡匿名類，也可以復制和修改示例代碼。 下一步是創建`Profiler`對象，傳遞`Timeable`對象和標題作為參數。 `Profiler`提供了`timingLoop`，它使用存儲為實例變量的`Timeable`。它多次調用`Timeable`對象上的`timeMe`方法，使用一系列的`n`值。`timingLoop`接受兩個參數： + `startN`是`n`的值，計時循環應該從它開始。 + `endMillis`是以毫秒為單位的閾值。隨著 `timingLoop`增加問題規模，運行時間增加；當運行時間超過此閾值時，`timingLoop`停止。 當你運行實驗時，你可能需要調整這些參數。如果`startN`太低，運行時間可能太短，無法準確測量。如果`endMillis`太低，你可能無法獲得足夠的數據，來查看問題規模和運行時間之間的明確關系。 這段代碼位于`ProfileListAdd.java`，你將在下一個練習中運行它。當我運行它時，我得到這個輸出： ``` 4000, 3 8000, 0 16000, 1 32000, 2 64000, 3 128000, 6 256000, 18 512000, 30 1024000, 88 2048000, 185 4096000, 242 8192000, 544 16384000, 1325 ``` 第一列是問題規模，`n`；第二列是以毫秒為單位的運行時間。前幾個測量非常嘈雜；最好將`startN`設置在`64000`左右。 `timingLoop`的結果是包含此數據的`XYSeries`。如果你將這個序列傳給`plotResults`，它會產生一個如圖 4.1 所示的圖形。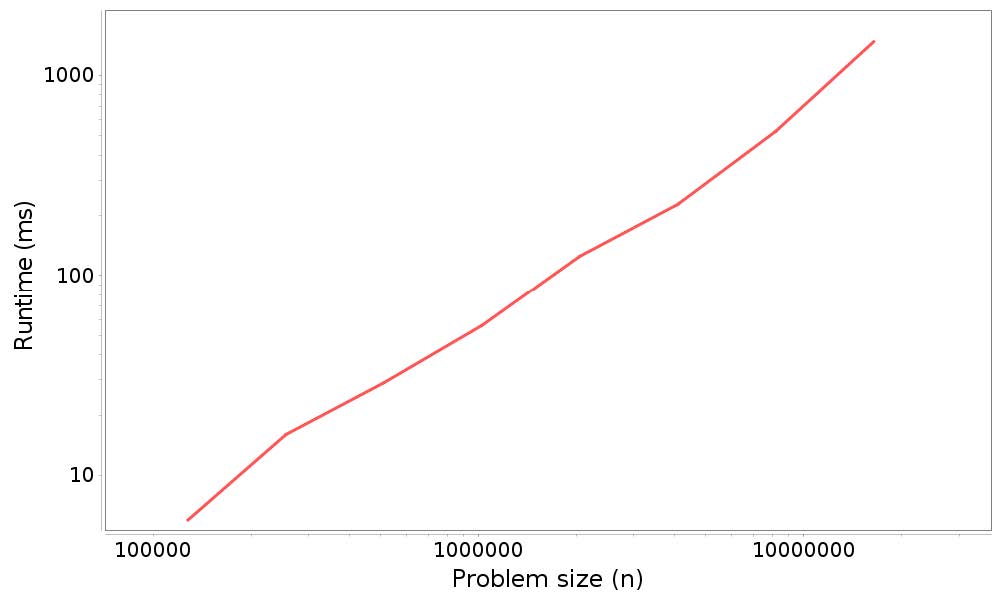  圖 4.1 分析結果：將`n`個元素添加到`ArrayList`末尾的運行時間與問題規模。 下一節解釋了如何解釋它。 ## 4.4 解釋結果 基于我們對`ArrayList`工作方式的理解，我們期望，在添加元素到最后時，`add`方法需要常數時間。所以添加`n`個元素的總時間應該是線性的。 為了測試這個理論，我們可以繪制總運行時間和問題規模，我們應該看到一條直線，至少對于大到足以準確測量的問題規模。在數學上，我們可以為這條直線編寫一個函數： ``` runtime = a + b * n ``` 其中`a`是線的截距，`b`是斜率。 另一方面，如果`add`是線性的，則`n`次添加的總時間將是平方。如果我們繪制運行時間與問題規模，我們預計會看到拋物線。或者在數學上，像： ``` runtime = a + b * n + c * n ** 2 ``` 有了完美的數據，我們可能能夠分辨直線和拋物線之間的區別，但如果測量結果很嘈雜，可能很難辨別。解釋嘈雜的測量值的更好方法是，在重對數刻度上繪制的運行時間和問題規模。 為什么？我們假設運行時間與`n ** k`成正比，但是我們不知道指數`k`是什么。我們可以將關系寫成這樣： ``` runtime = a + b * n + … + c * n ** k ``` 對于`n`的較大值，最大指數項是最重要的，因此： ``` runtime ≈ c * n ** k ``` 其中`≈`意思是“大致相等”。現在，如果我們對這個方程的兩邊取對數： ``` log(runtime) ≈ log(c) + k * log(n) ``` 這個方程式意味著，如果我們在重對數合度上繪制運行時間與`n`，我們預計看到一條直線，截距為`log(c)`，斜率為`k`。我們不太在意截距，但斜率表示增長級別：如果`k = 1`，算法是線性的；如果`k = 2`，則為平方的。 看上一節中的數字，你可以通過眼睛來估計斜率。但是當你調用`plotResults`它時，會計算數據的最小二乘擬合并打印估計的斜率。在這個例子中： ``` Estimated slope = 1.06194352346708 ``` 它接近`1`；并且這表明`n`次添加的總時間是線性的，所以每個添加是常數時間，像預期的那樣。 其中重要的一點：如果你在圖形看到這樣的直線，這并不意味著該算法是線性的。如果對于任何指數`k`，運行時間與`n ** k`成正比，我們預計看到斜率為`k`的直線。如果斜率接近`1`，則表明算法是線性的。如果接近`2`，它可能是平方的。 ## 4.5 練習 4 在本書的倉庫中，你將找到此練習所需的源文件： + `Profiler.java`包含上述`Profiler`類的實現。你會使用這個類，但你不必知道它如何工作。但可以隨時閱讀源碼。 + `ProfileListAdd.java`包含此練習的起始代碼，包括上面的示例，它測量了`ArrayList.add`。你將修改此文件來測量其他一些方法。 此外，在`code`目錄中，你將找到 Ant 構建文件`build.xml`。 運行`ant ProfileListAdd`來運行`ProfileListAdd.java`。你應該得到類似圖 4.1 的結果，但是你可能需要調整`startN`或`endMillis`。估計的斜率應該接近`1`，表明執行`n`個添加操作的所需時間與`n`成正比；也就是說，它是`O(n)`的。 在`ProfileListAdd.java`中，你會發現一個空的方法`profileArrayListAddBeginning`。用測試`ArrayList.add`的代碼填充這個方法的主體，總是把新元素放在開頭。如果你以`profileArrayListAddEnd`的副本開始，你只需要進行一些更改。在`main`中添加一行來調用這個方法。 再次運行`ant ProfileListAdd`并解釋結果。基于我們對`ArrayList`工作方式的理解，我們期望，每個添加操作是線性的，所以`n`次添加的總時間應該是平方的。如果是這樣，在重對數刻度中，直線的估計斜率應該接近`2`。是嗎？ 現在我們來將其與`LinkedList`比較。當我們把新元素放在開頭，填充`profileLinkedListAddBeginning`并使用它劃分`LinkedList.add`。你期望什么性能？結果是否符合你的期望？ 最后，填充`profileLinkedListAddEnd`的主體，使用它來劃分`LinkedList.add`。你期望什么性能？結果是否符合你的期望？ 我將在下一章中展示結果并回答這些問題。