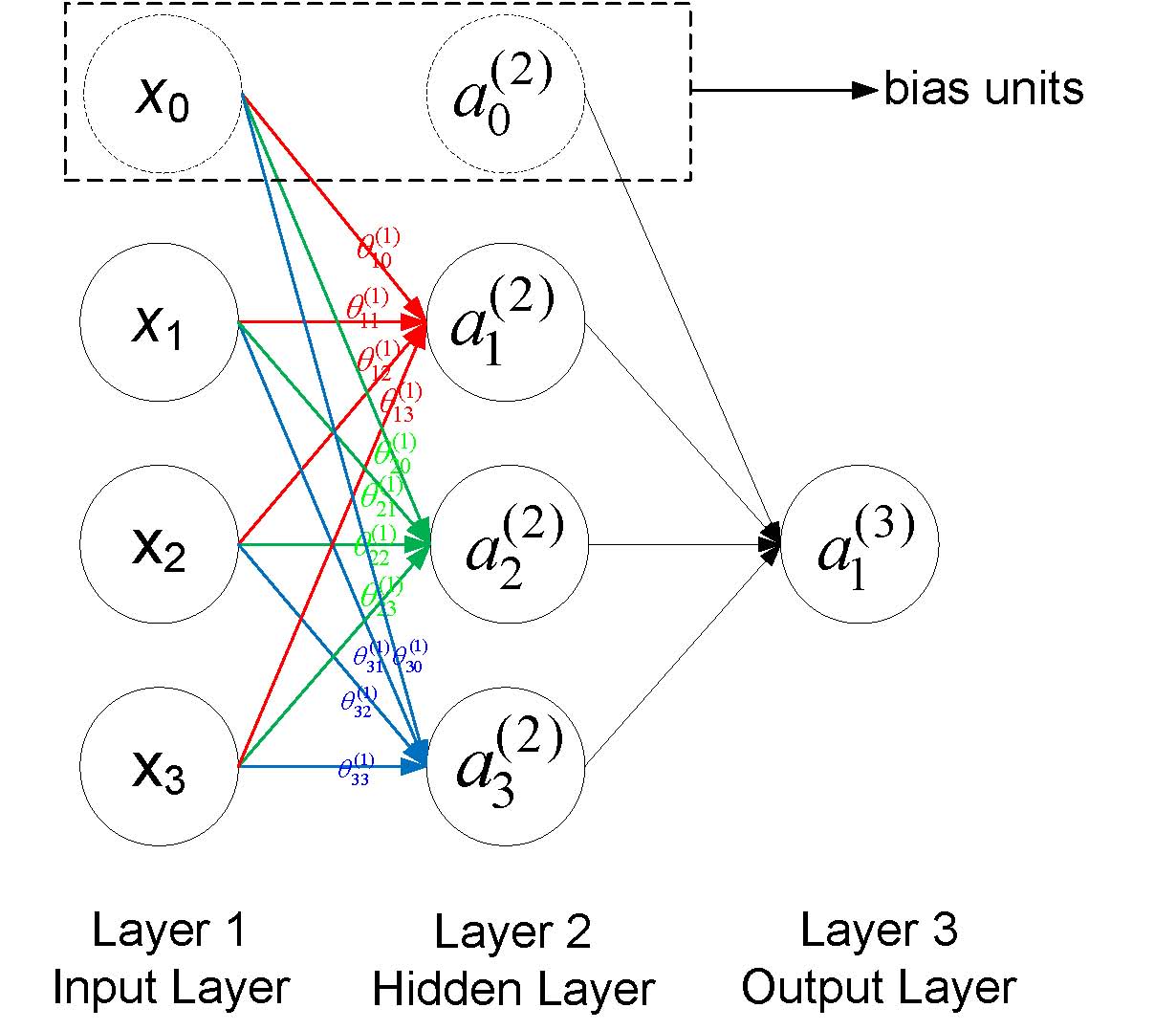
# [神經網絡(Neural Network)——表示](https://www.cnblogs.com/python27/p/MachineLearningWeek04.html) ## 動機(Motivation) 對于非線性分類問題，如果用多元線性回歸進行分類，需要構造許多高次項，導致特征特多學習參數過多，從而復雜度太高。 ## 神經網絡(Neural Network) 一個簡單的神經網絡如下圖所示，每一個圓圈表示一個神經元，每個神經元接收上一層神經元的輸出作為其輸入，同時其輸出信號到下一層，其中每一層的第一個神經元稱為bias unit，它是額外加入的其值為1，通常用+1表示,下圖用虛線畫出。  符號說明： * a(j)i 表示第j層網絡的第i個神經元，例如下圖a(2)1* 就表示第二層的第一個神經元 * θ(j) 表示從第j層到第j+1層的權重矩陣，例如下圖所有的θ(1)* 表示從第一層到第二層的權重矩陣 * θ(j)uv 表示從第j層的第v個神經元到第j+1層的第u個神經的權重，例如下圖中θ(1)23* 表示從第一層的第3個神經元到第二層的第2個神經元的權重，需要注意到的是下標uv是指v->u的權重而不是u->v，下圖也給出了第一層到第二層的所有權重標注 * 一般地，如果第j層有sj 個神經元（不包括bias神經元），第j+1層有sj+1個神經元（也不包括bias神經元），那么權重矩陣θj的維度是(sj+1×sj+1) ## 前向傳播(Forward Propagration, FP) 后一層的神經元的值根據前一層神經元的值的改變而改變，以上圖為例，第二層的神經元的更新方式為 a(2)1\=g(θ(1)10x0+θ(1)11x1+θ(1)12x2+θ(1)13x3) a(2)2\=g(θ(1)20x0+θ(1)21x1+θ(1)22x2+θ(1)23x3) a(2)3\=g(θ(1)30x0+θ(1)31x1+θ(1)32x2+θ(1)33x3) a(2)4\=g(θ(1)40x0+θ(1)41x1+θ(1)42x2+θ(1)43x3) 其中g(z)為sigmoid函數，即g(z)\=11+e?z ### 1\. 向量化實現(Vectorized Implementation) 如果我們以向量角度來看待上述的更新公式，定義 a(1)\=x\=?????x0x1x2x3????? ? ?z(2)\=?????z(2)1z(2)1z(2)1????? ? ?θ(1)\=?????θ(1)10θ(1)20θ(1)30θ(1)11θ(1)21θ(1)31θ(1)12θ(1)22θ(1)32θ(1)13θ(1)23θ(1)33????? 則更新公式可以簡化為 z(2)\=θ(1)a(1) a(2)\=g(z(2)) z(3)\=θ(2)a(2) a(3)\=g(z(3))\=hθ(x) 可以看到，我們由第一層的值，計算第二層的值；由第二層的值，計算第三層的值，得到預測的輸出，計算的方式一層一層往前走的，這也是***前向傳播***的名稱由來。 ### 2\. 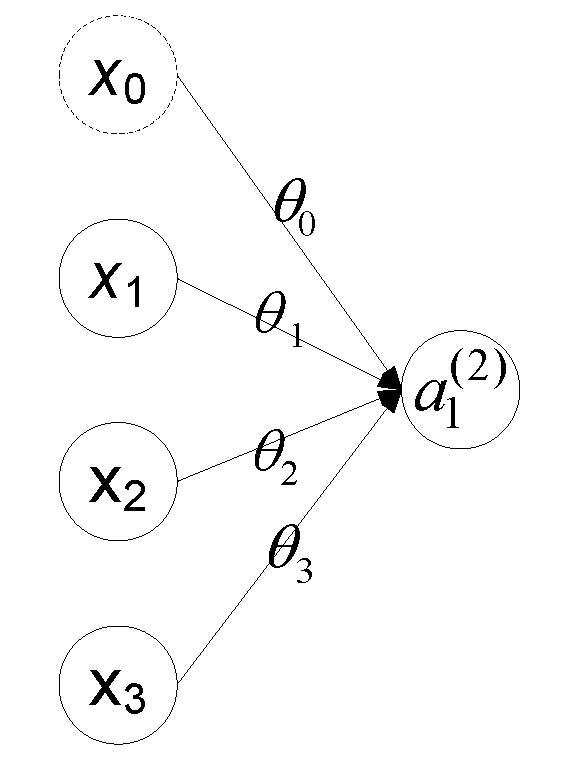與Logistic回歸的聯系  考慮上圖沒有隱藏層的神經網絡，其中x\=?????x0x1x2x3????? ，θ\=\[θ0θ1θ2θ3\]，則我們有hθ(x)\=a(2)1\=g(z(1))\=g(θx)\=g(x0θ0+x1θ1+x2θ2+x3θ3) ，可以看到這**正是Logistic回歸的假設函數！！！**這種關系表明Logistic是回歸是不含隱藏層的特殊神經網絡，神經網絡從某種程度上來說是對logistic回歸的推廣。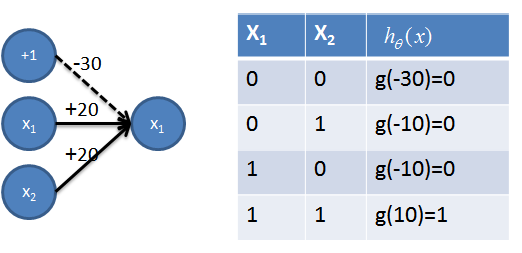 ## 神經網絡示例 對于如下圖所示的線性不可分的分類問題，(0,0)(1,1)為一類(0,1)(1,0)為另一類，神經網絡可以解決（見5）。首先需要一些簡單的神經網絡(1-4)，其中圖和真值表結合可以清楚的看出其功能，不再贅述。  ### 1\. 實現AND操作  ### 2\. 實現OR操作  ### 3\. 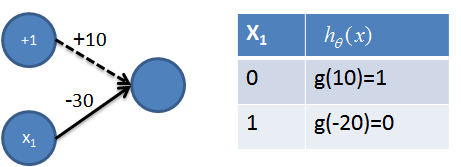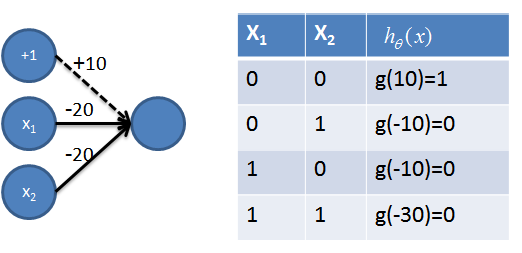實現非操作  ### 4\. 實現NAND=((not x1) and (not x2))操作  ### 5\. 組合實現NXOR=NOT(x1 XOR x2) 操作? 該神經網絡用到了之前的AND操作（用紅色表示）、NAND操作（用青色表示）和OR操作（用橙色表示），從真值表可以看出，該神經網絡成功地將(0, 0)(1,1)分為一類，(1,0)(0,1)分為一類，很好解決了線性不可分的問題。  ## 神經網絡的代價函數(含正則項) J(Θ)\=?1m\[∑i\=1m∑k\=1Ky(i)klog(hθ(x(i)))k+(1?y(i)k)log(1?(hθ(x(i)))k)\]+λ2m∑l\=1L?1∑i\=1sl∑j\=1sl+1(Θ(l)ji)2 符號說明： * m * — 訓練example的數量 * K ?—?最后一層（輸出層）的神經元的個數，也等于分類數（分K類，K≥3* ） * y(i)k —?第i個訓練exmaple的輸出(長度為K個向量)的第k* 個分量值 * (hθ(x(i)))k —?對第i個example用神經網絡預測的輸出(長度為K的向量)的第k* 個分量值 * L * ?—?神經網絡總共的層數（包括輸入層和輸出層） * Θ(l) ?—?第l層到第l+1* 層的權重矩陣 * sl ?—?第l層神經元的個數, 注意i* 從1開始計數，bias神經元的權重不算在正則項內 * sl+1 ?—?第l+1 * 層神經元的個數 ## 參考文獻 ?\[1\]?Andrew Ng Coursera 公開課第四周 ?\[2\] Neural Networks.?https://www.doc.ic.ac.uk/~nd/surprise\_96/journal/vol4/cs11/report.html ?\[3\] The nature of code.?http://natureofcode.com/book/chapter-10-neural-networks/ ?\[4\]?A Basic Introduction To Neural Networks.?http://pages.cs.wisc.edu/~bolo/shipyard/neural/local.html