牛頓迭代法求局部最優(解)20200310 · 神經網絡&深度學習2020

``` //在 Qt5.x 編譯qmake通過……2020年1月: #include "mainwindow.h" #include <QApplication> #include "qdebug.h" struct struc_X1X2 //放(2Ci二次函數的）兩個根(的數據）結構： { double x1; double x2; };// struc_X1X2 x1x2_001; //---------------------------------------------------------------- //求（2Ci二次函數的）函數值 double func_Fx(double x, double a1, double b, double c,double y=0)// { double tmp_fx= a1*x*x+ b*x+ c; return tmp_fx; }// //---------------------------------------------------------------- // 用極值公式，求（2Ci二次函數）的極值： double fun_extremValue(double a1, double b, double c, double y=0)// { double tmp_y= 4.0*a1*c-b*b; return (tmp_y/(4.0*a1) ); }// //--------------------------------------------------------------------------- //用求根公式，求（2Ci二次函數）的兩個根：注意形參 &x1,&x2……傳遞進入(子)函數的用法： struc_X1X2 func_x1x2(double aa, double b, double c, double * x1, double * x2)// { double tmp_y= sqrt(double(qAbs(double( b*b-4.0*aa*c ) ) ) ); //(b方- 4ac)并開平方 (*x1)= (-1.0*b - tmp_y)/ (2.0*aa); (*x2)= (-1.0*b+ tmp_y) /(2.0*aa); x1x2_001.x1= double(-1.0*b - tmp_y)/ (2.0*aa); x1x2_001.x2= double(-1.0*b + tmp_y)/ (2.0*aa); return x1x2_001; }// //--------------------- //（二次函數）的導函數的計算(函數): double func_di_fx(double x, double a, double b)// { double tmp_di_y= 2.0* a* x + b; return tmp_di_y; }// int main(int argc, char *argv[]) { QApplication a(argc, argv); MainWindow w; w.show(); // qDebug()<< "log test - Debug"; double x0_0=-20.0; //10.0;//-20.0;//給 X0賦予初值 2.0;//1.0;//1.0; //-10.0; double tmp_Fx; double tmp_Di_fx; double aa=1.0; double b=2.0;//2.0; double c=-1.0;//0.0;//3.0; double x0_01= x0_0-( func_Fx(x0_0,aa,b,c,0) / func_di_fx(x0_0,aa,b) ); //用 x0的值,(第1次)試用牛頓迭代公式,計算X1的值 double Xn_old01=x0_01; //準備迭代,所以把 X1的值先放在 X(n-1)這個變量(Xn_old01）里待用 double X_n=0.0; //= Xn_old01; // X_n賦予初值 (無實際意義)與 X_n=0.0;等效 // double X_extremV=fun_extremValue(aa,b,c,0.0); //用極值公式計算極值 //下面迭代 double x1=0.0; double x2=0.0; //初始化兩個變量,放(二次函數)的兩個根 func_x1x2(aa,b,c, &x1,&x2); //（用求根公式）求根，并放在 (x1,x2) 當中，注意形參 &x1,&x2的用法。 for(int i=1;i<99;++i)// { tmp_Fx= func_Fx(Xn_old01 , aa, b, c, 0); //計算函數 F(x)=Y 的值 tmp_Di_fx= func_di_fx(Xn_old01, aa, b); //計算導函數 f'(x)= y' 的值 //double X_n= (double)Xn_old01- ( (double)tmp_Fx/ tmp_Di_fx); //這就是著名的牛頓迭代公式 qDebug()<<"F(x(n-1)):"<<tmp_Fx<<", Dfx(n-1)"<<tmp_Di_fx; qDebug()<< "第NoId:"<< i; qDebug()<< "次迭代,求得的根x(n):"; qDebug() <<X_n << ", 求根與極值之間的差(這個errorValue代替誤差)X(trun)-X(x):=" <<( X_extremV- X_n ) << "] x1,x2:=:"<< x1x2_001.x1<<","<< x1x2_001.x2<< " ;"; Xn_old01= X_n; }//for110i // qDebug("如果只寫在括號里，是不需要QDebug頭文件的 %d %s", 1.2, "3.4"); // return a.exec(); }// ``` 迭代99次以后的結果： ``` F(x(n-1)): 89.2528 , Dfx(n-1) -19.1053 x(n): -5.881 , X(trun)-X(x):= 3.881 ] x1,x2:=: -2.41421 , 0.414214 ; F(x(n-1)): 21.8242 , Dfx(n-1) -9.762 x(n): -3.64538 , X(trun)-X(x):= 1.64538 ] x1,x2:=: -2.41421 , 0.414214 ; F(x(n-1)): 4.99801 , Dfx(n-1) -5.29075 x(n): -2.70071 , X(trun)-X(x):= 0.700706 ] x1,x2:=: -2.41421 , 0.414214 ; F(x(n-1)): 0.892401 , Dfx(n-1) -3.40141 x(n): -2.43834 , X(trun)-X(x):= 0.438344 ] x1,x2:=: -2.41421 , 0.414214 ; F(x(n-1)): 0.0688337 , Dfx(n-1) -2.87669 x(n): -2.41442 , X(trun)-X(x):= 0.414416 ] x1,x2:=: -2.41421 , 0.414214 ; F(x(n-1)): 0.000572555 , Dfx(n-1) -2.82883 x(n): -2.41421 , X(trun)-X(x):= 0.414214 ] x1,x2:=: -2.41421 , 0.414214 ; F(x(n-1)): 4.09657e-08 , Dfx(n-1) -2.82843 x(n): -2.41421 , X(trun)-X(x):= 0.414214 ] x1,x2:=: -2.41421 , 0.414214 ; F(x(n-1)): 0 , Dfx(n-1) -2.82843 ``` 觀察結果，幾次（6次）以后…就穩定、并且收斂了…… ![](https://img.kancloud.cn/a9/ce/a9cedf494d3fc5460435ca64f9351e3e_951x983.jpg)![](https://img.kancloud.cn/2a/08/2a08fd7a300341b5d87a3bf24ea5670b_971x1221.jpg)![](https://img.kancloud.cn/e6/af/e6af46a343c7a34e99ee3a90867e9e0d_953x1213.jpg) ![](https://img.kancloud.cn/fc/4d/fc4da37a58824ad021dfecc4d91e4598_963x1229.jpg) ![](https://img.kancloud.cn/f6/28/f628dd7a7aad2390c89d41c35a3c6657_955x1247.jpg) ![](https://img.kancloud.cn/ca/29/ca29b685744d35b1f4d0a6beaa58bcf8_973x1029.jpg) 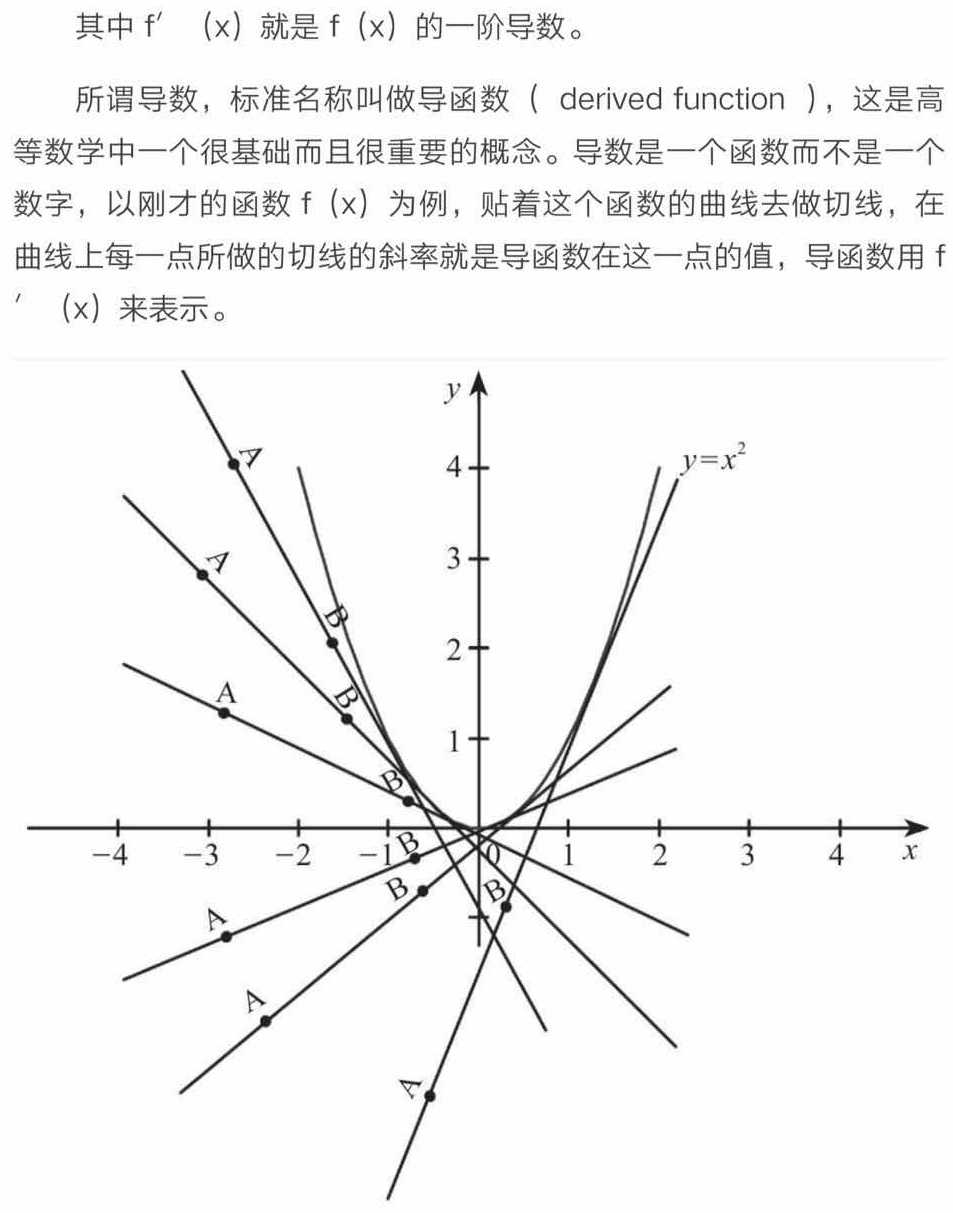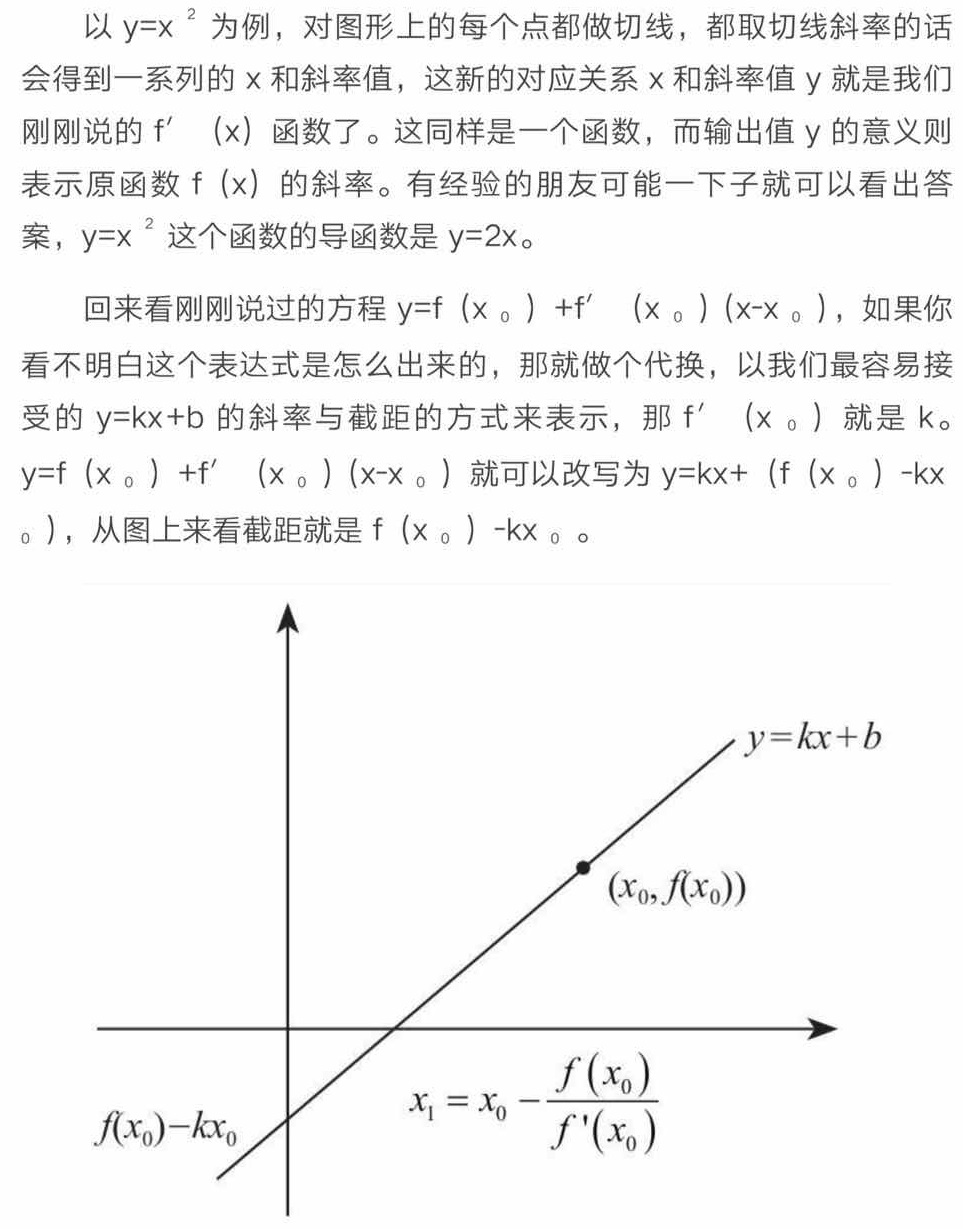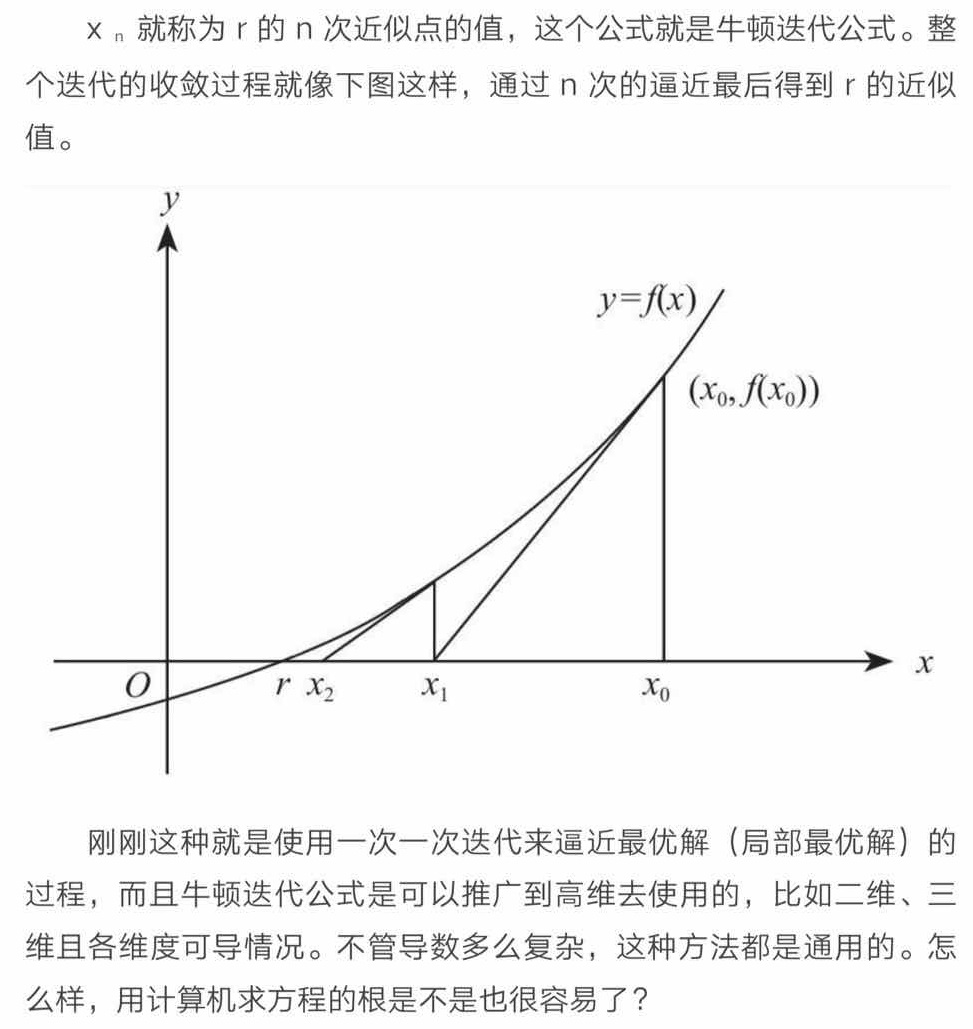再運行一遍： p, li { white-space: pre-wrap; } ~~~ double x0_0=10.0;//-20.0;//給 X0賦予初值 ~~~ ``` F(x(n-1)): 29.2583 , Dfx(n-1) 11.1818 ??NoId: 1 ???????????????x(n): 1.97432 , ???????????????????????errorValue????????)X(trun)-X(x):= -3.97432 ] x1,x2:=: -2.41421 , 0.414214 ; F(x(n-1)): 6.84656 , Dfx(n-1) 5.94863 ??NoId: 2 ???????????????x(n): 0.82337 , ???????????????????????errorValue????????)X(trun)-X(x):= -2.82337 ] x1,x2:=: -2.41421 , 0.414214 ; F(x(n-1)): 1.32468 , Dfx(n-1) 3.64674 ??NoId: 3 ???????????????x(n): 0.46012 , ???????????????????????errorValue????????)X(trun)-X(x):= -2.46012 ] x1,x2:=: -2.41421 , 0.414214 ; F(x(n-1)): 0.13195 , Dfx(n-1) 2.92024 ??NoId: 4 ???????????????x(n): 0.414935 , ???????????????????????errorValue????????)X(trun)-X(x):= -2.41494 ] x1,x2:=: -2.41421 , 0.414214 ; F(x(n-1)): 0.00204167 , Dfx(n-1) 2.82987 ??NoId: 5 ???????????????x(n): 0.414214 , ???????????????????????errorValue????????)X(trun)-X(x):= -2.41421 ] x1,x2:=: -2.41421 , 0.414214 ; F(x(n-1)): 5.20519e-07 , Dfx(n-1) 2.82843 ??NoId: 6 ???????????????x(n): 0.414214 , ???????????????????????errorValue????????)X(trun)-X(x):= -2.41421 ] x1,x2:=: -2.41421 , 0.414214 ; F(x(n-1)): 3.37508e-14 , Dfx(n-1) 2.82843 ??NoId: 7 ???????????????x(n): 0.414214 6次以后收斂、并且穩定。 ``` 第3次運行： double x0_0=-20.0;//給 X0賦予初值 ``` F(x(n-1)): 89.2528 , Dfx(n-1) -19.1053 ??NoId: 1 ???????????????x(n): -5.881 , ???????????????????????errorValue????????)X(trun)-X(x):= 3.881 ] x1,x2:=: -2.41421 , 0.414214 ; F(x(n-1)): 21.8242 , Dfx(n-1) -9.762 ??NoId: 2 ???????????????x(n): -3.64538 , ???????????????????????errorValue????????)X(trun)-X(x):= 1.64538 ] x1,x2:=: -2.41421 , 0.414214 ; F(x(n-1)): 4.99801 , Dfx(n-1) -5.29075 ??NoId: 3 ???????????????x(n): -2.70071 , ???????????????????????errorValue????????)X(trun)-X(x):= 0.700706 ] x1,x2:=: -2.41421 , 0.414214 ; F(x(n-1)): 0.892401 , Dfx(n-1) -3.40141 ??NoId: 4 ???????????????x(n): -2.43834 , ???????????????????????errorValue????????)X(trun)-X(x):= 0.438344 ] x1,x2:=: -2.41421 , 0.414214 ; F(x(n-1)): 0.0688337 , Dfx(n-1) -2.87669 ??NoId: 5 ???????????????x(n): -2.41442 , ???????????????????????errorValue????????)X(trun)-X(x):= 0.414416 ] x1,x2:=: -2.41421 , 0.414214 ; F(x(n-1)): 0.000572555 , Dfx(n-1) -2.82883 ??NoId: 6 ???????????????x(n): -2.41421 , ???????????????????????errorValue????????)X(trun)-X(x):= 0.414214 ] x1,x2:=: -2.41421 , 0.414214 ; F(x(n-1)): 4.09657e-08 , Dfx(n-1) -2.82843 ??NoId: 7 ???????????????x(n): -2.41421 , ???????????????????????errorValue????????)X(trun)-X(x):= 0.414214 ] x1,x2:=: -2.41421 , 0.414214 ; F(x(n-1)): 0 , Dfx(n-1) -2.82843 ??NoId: 8 ???????????????x(n): -2.41421 , ???????????????????????errorValue????????)X(trun)-X(x):= 0.414214 ] x1,x2:=: -2.41421 , 0.414214 ; F(x(n-1)): 0 , Dfx(n-1) -2.82843 ``` 請看：利用牛頓迭代法（Newton Iteration Method）求（2Ci二次函數的數值解）6次以后，就穩定、并且收斂到（局部）極值（局部最優解）了。 Qt支持中文不好，所以 ?(問號）都是中文提示……請忽略……