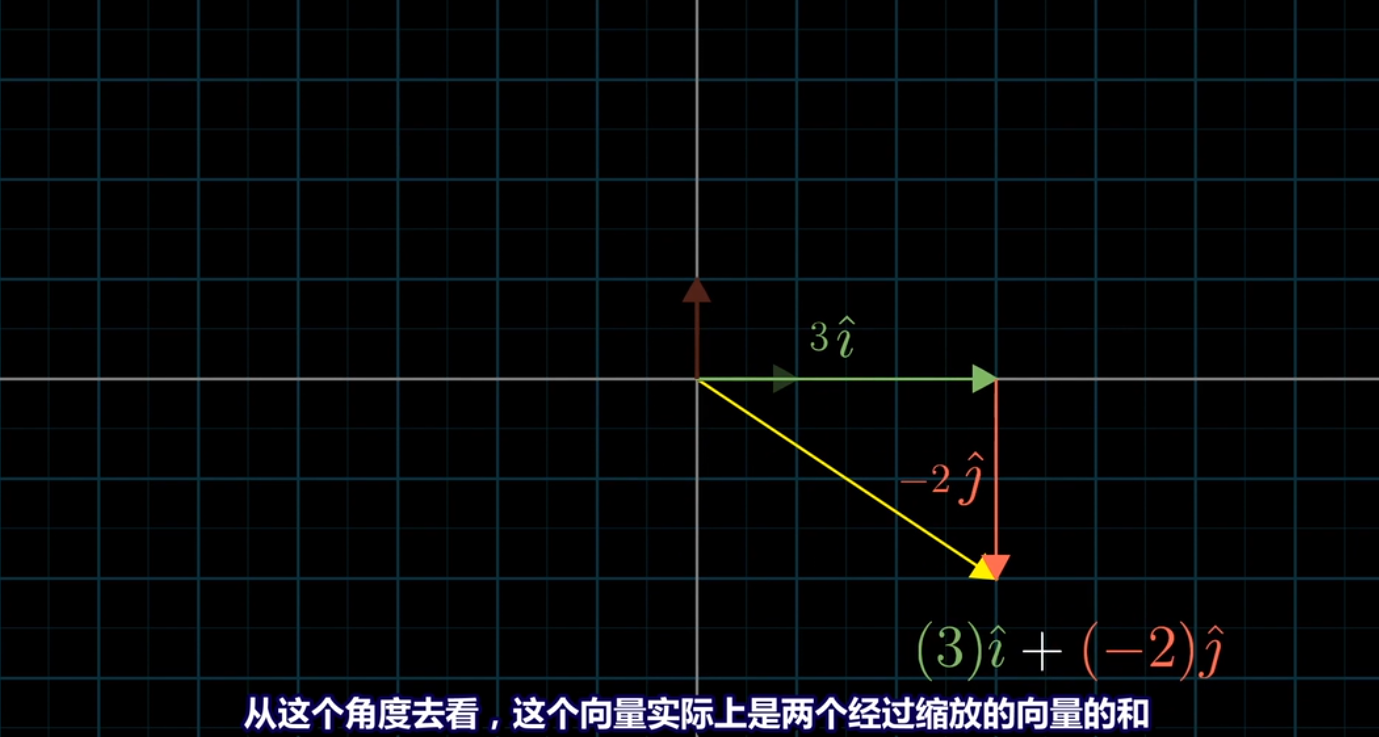
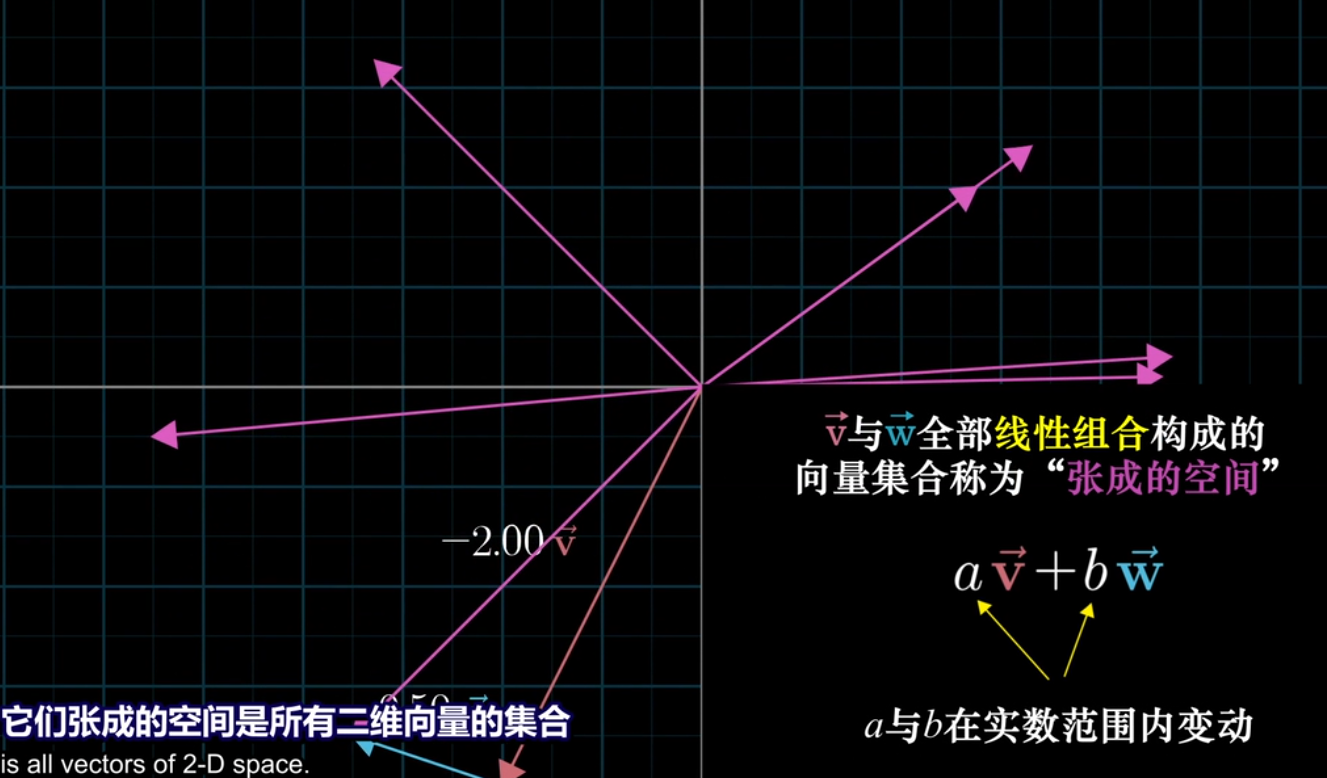
二維平面中任一向量都可以通過基向量的線性組合得到。 i帽，x方向的單位向量。j帽，y方向的單位向量。i與j是xy坐標系的“基向量" 將每個坐標看作標量，[3 -2] 等于 3i+(-2j)  **線性組合** 兩個向量分別與標量乘法和被稱為這兩個向量的線性組合。 標量：就是前面的常數 *****  1.兩個向量與標量乘法和產生二維空間內所有向量。 2.兩個向量與標量乘法和產生的向量都在一條直線上。 3.兩個向量都是零向量，只能在原點。 ***** 向量從原點出發，所以可以用向量的終點代表向量。把一個向量看作箭頭，都多個向量看作這些向量的終點坐標。 **線性相關** 若一個向量與另一個向量數乘之和后，對張成的空間沒有貢獻。移除后，不減小張成的空間，術語稱它們是線性相關的。 **線性無關** 所有向量都給張成的空間增添了新的維度，稱它們線性無關。 ***** 對于向量u,向量v和向量w，判斷它們是否線性無關。不成立，線性無關。