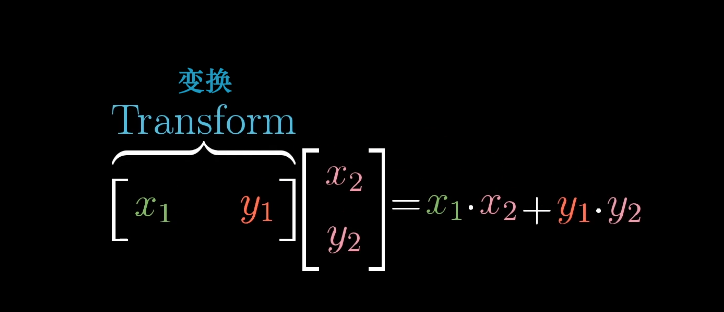
## 向量點積的幾何意義
**向量點積代數定義**

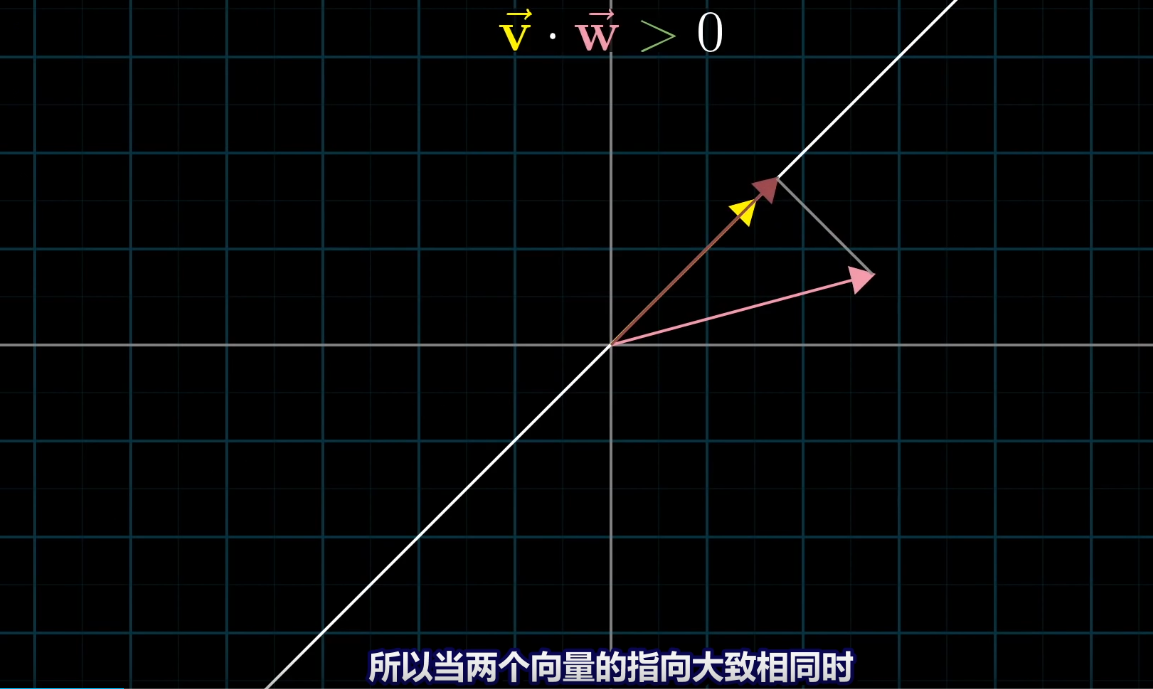
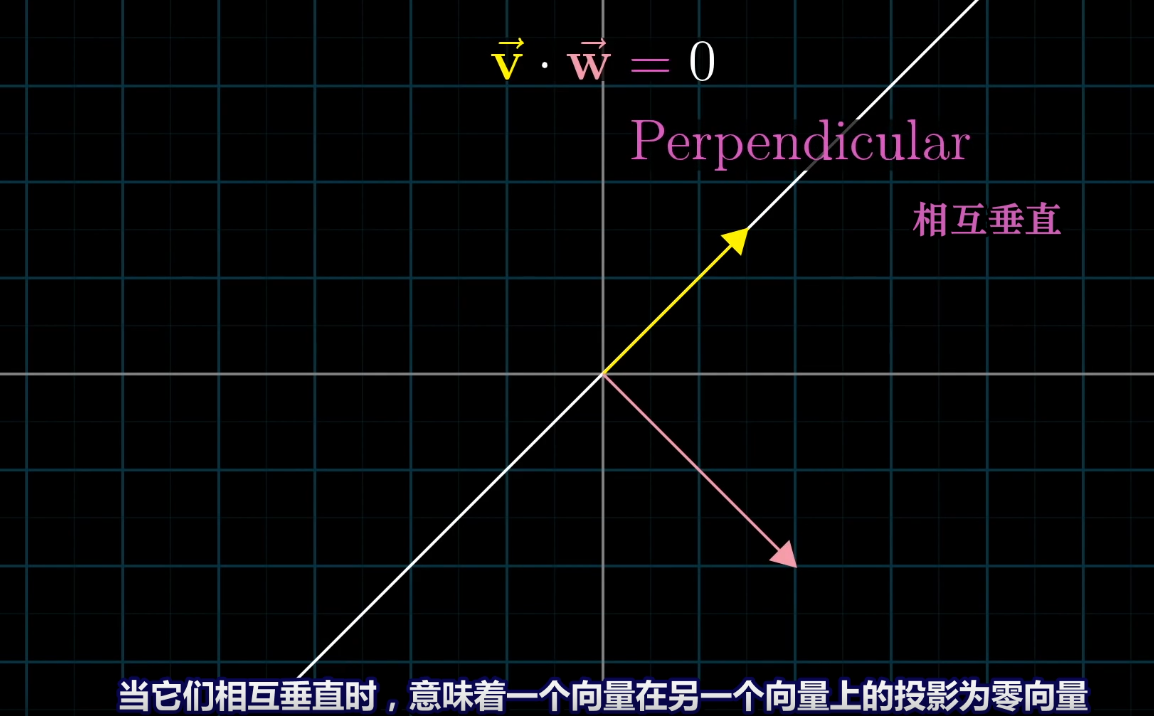

根據對稱性,v和w互相投射結果都一樣


*****
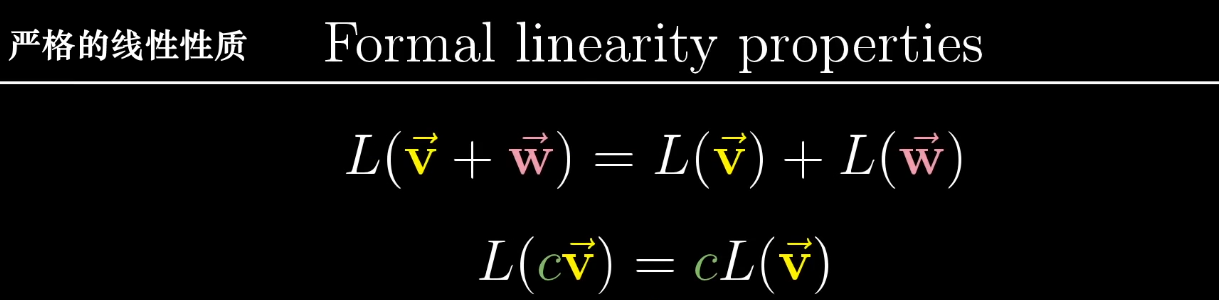

*****
**點積的代數定義**


*****
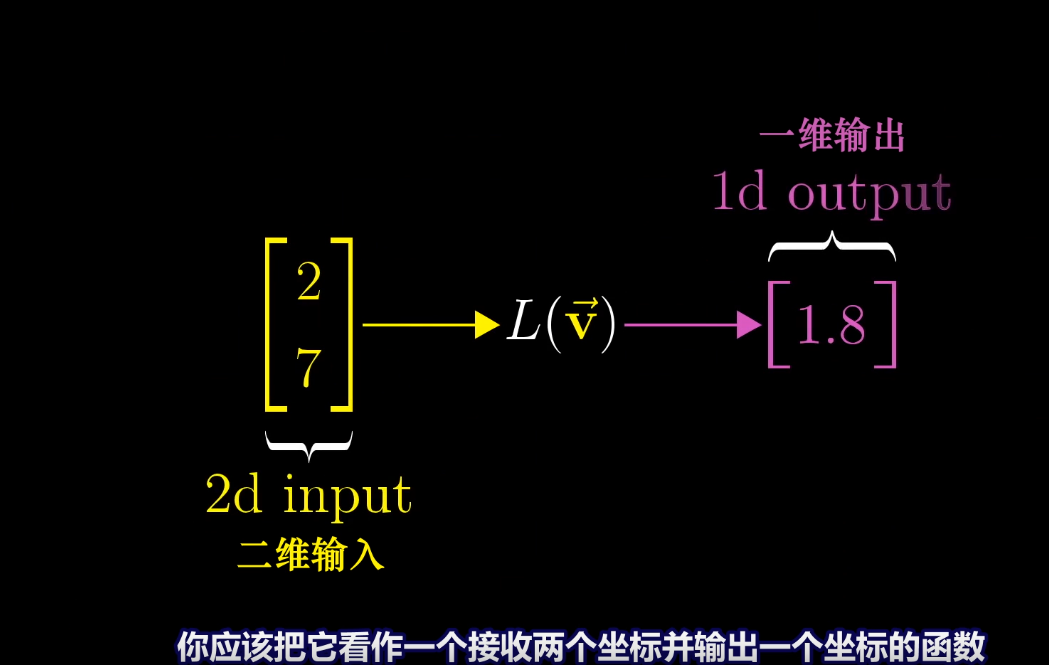
**1*2矩陣的幾何意義**
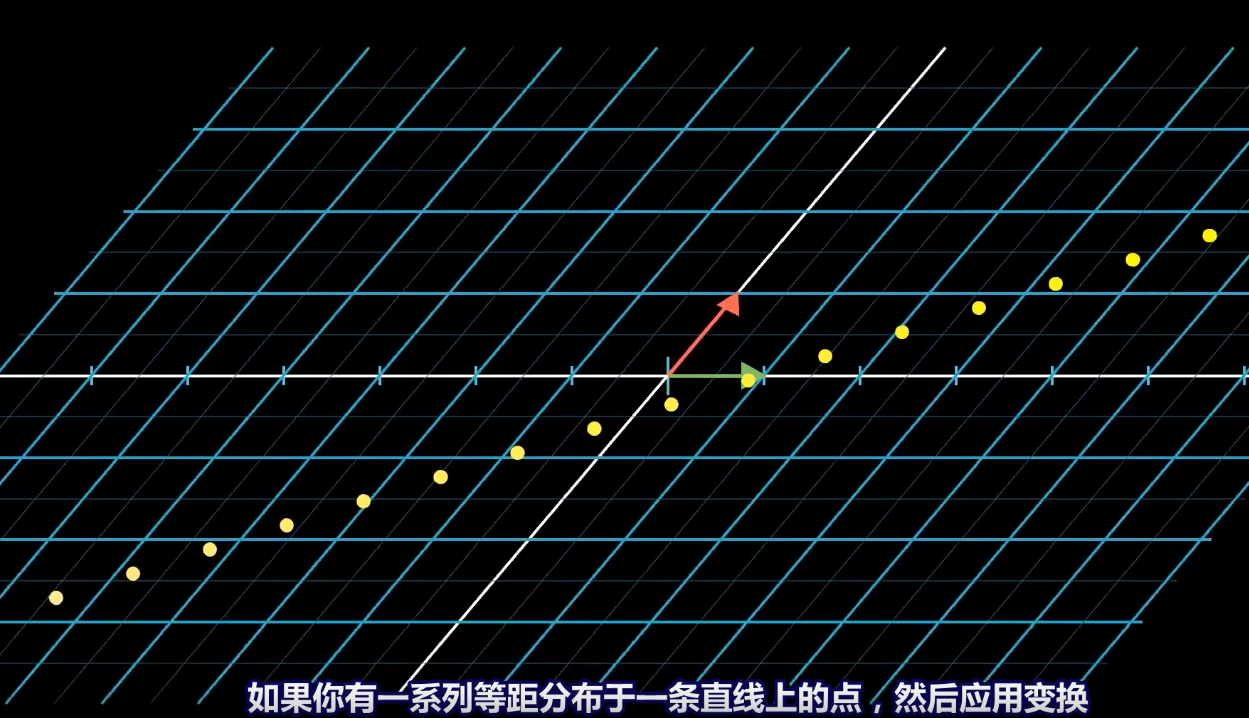
這個矩陣是一個線性變換,表示二維空間的兩個基向量i和j通過線性變換,兩個基向量落在一個一維數軸上,i和j的坐標對應與x軸重合的數軸的2和1兩個點

對一個向量向量進行[1 -2]的線性變換,最后向量與1*2矩陣的乘積為2。因為i落在1上,j落在-2上。該向量由4個i和3個j合成,如下圖,該向量的x方向分量落在4上,y方向分量落在-6上,4+(-6) = -2
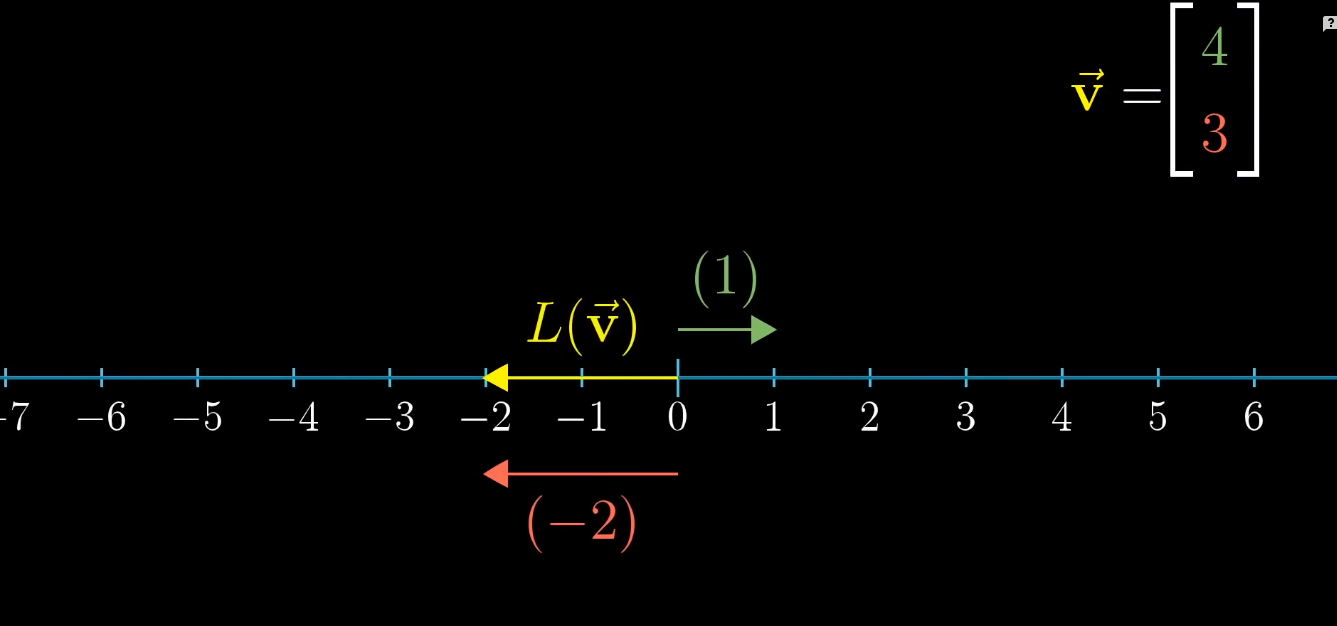
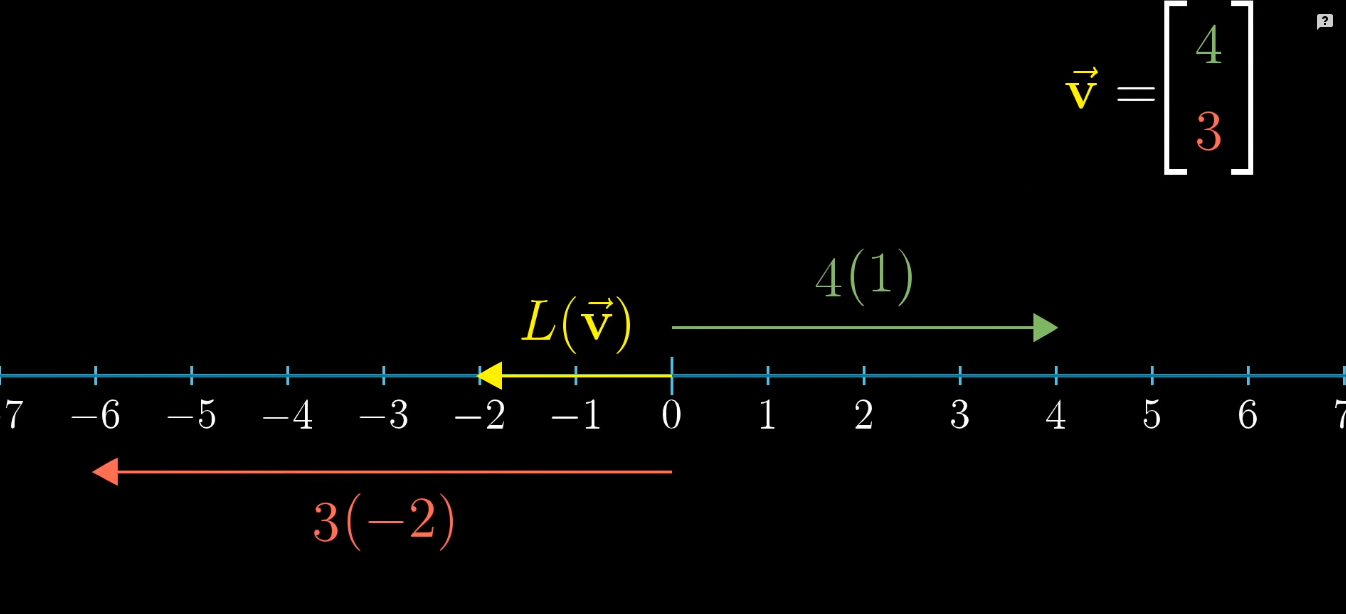
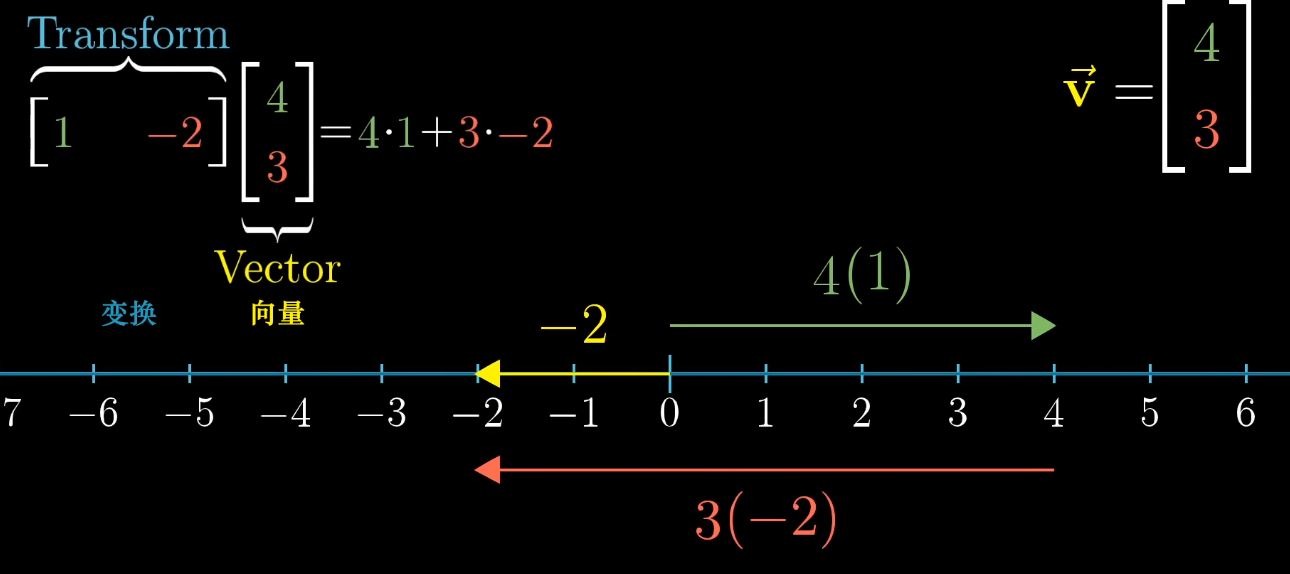
**該變換根據以下線性規則:**
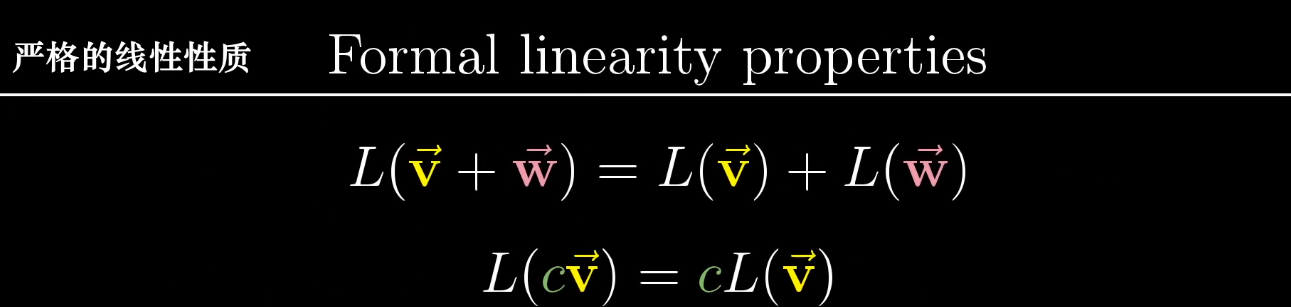
*****
*****

*****
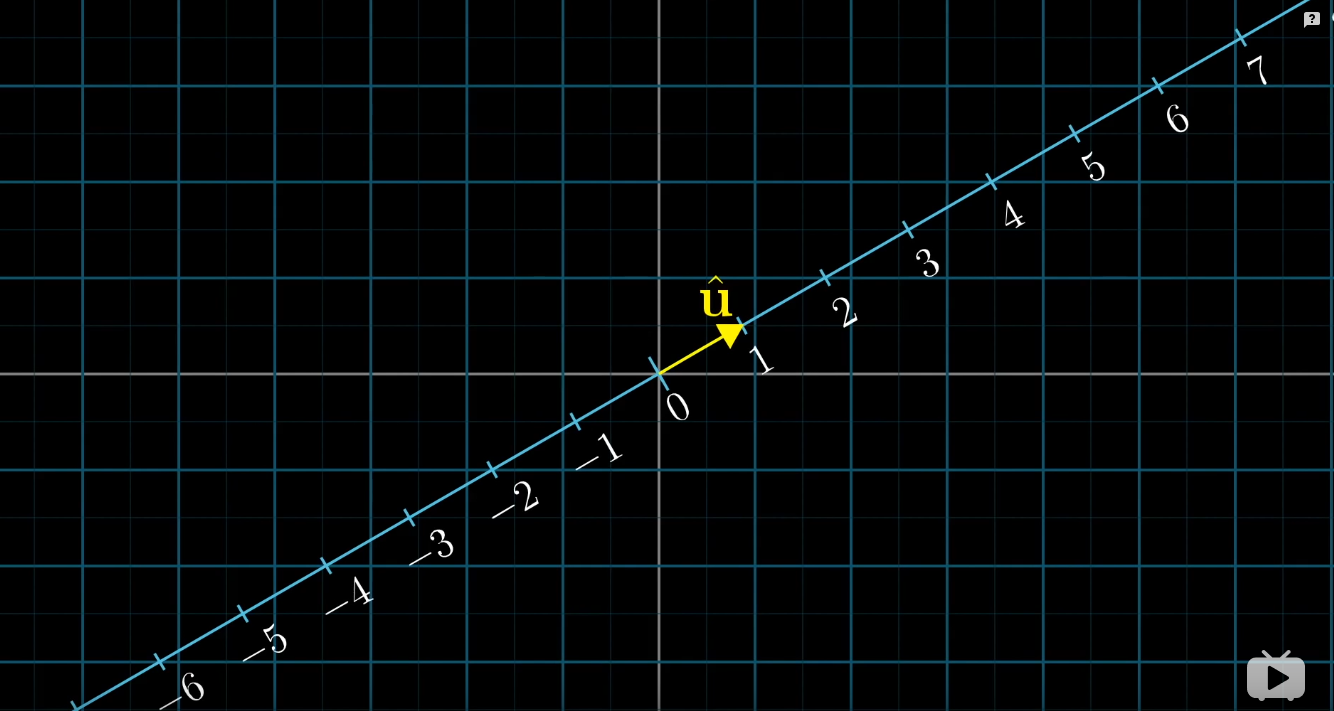
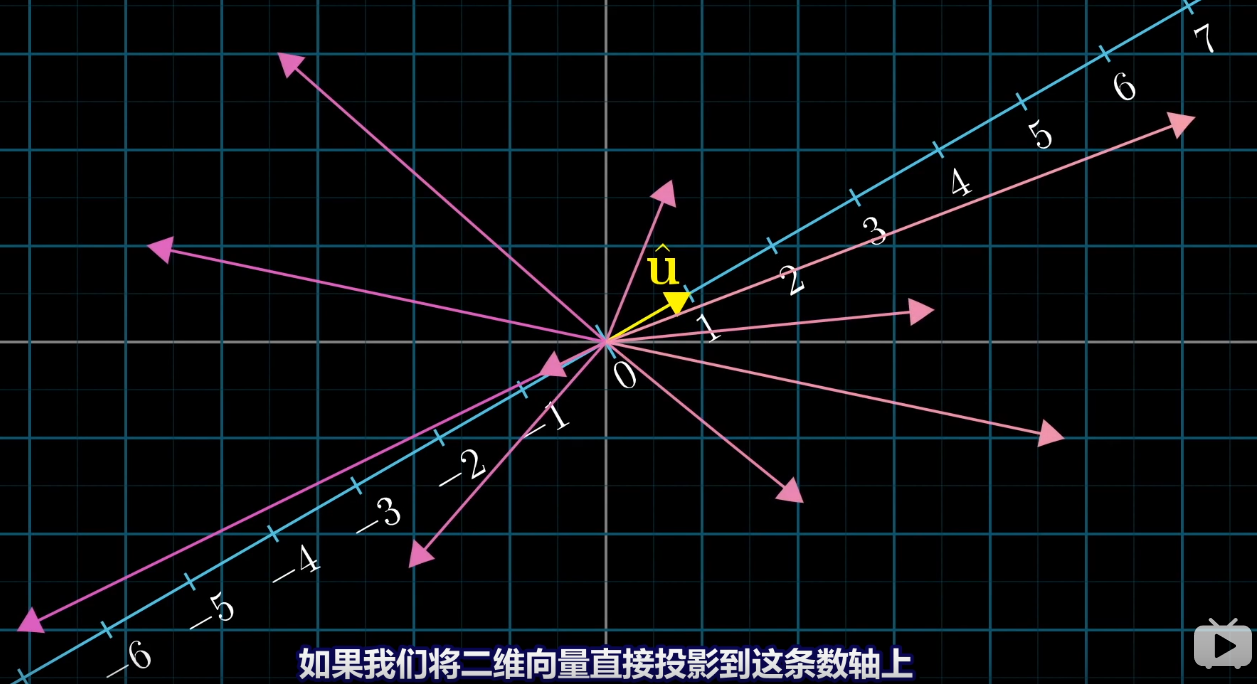
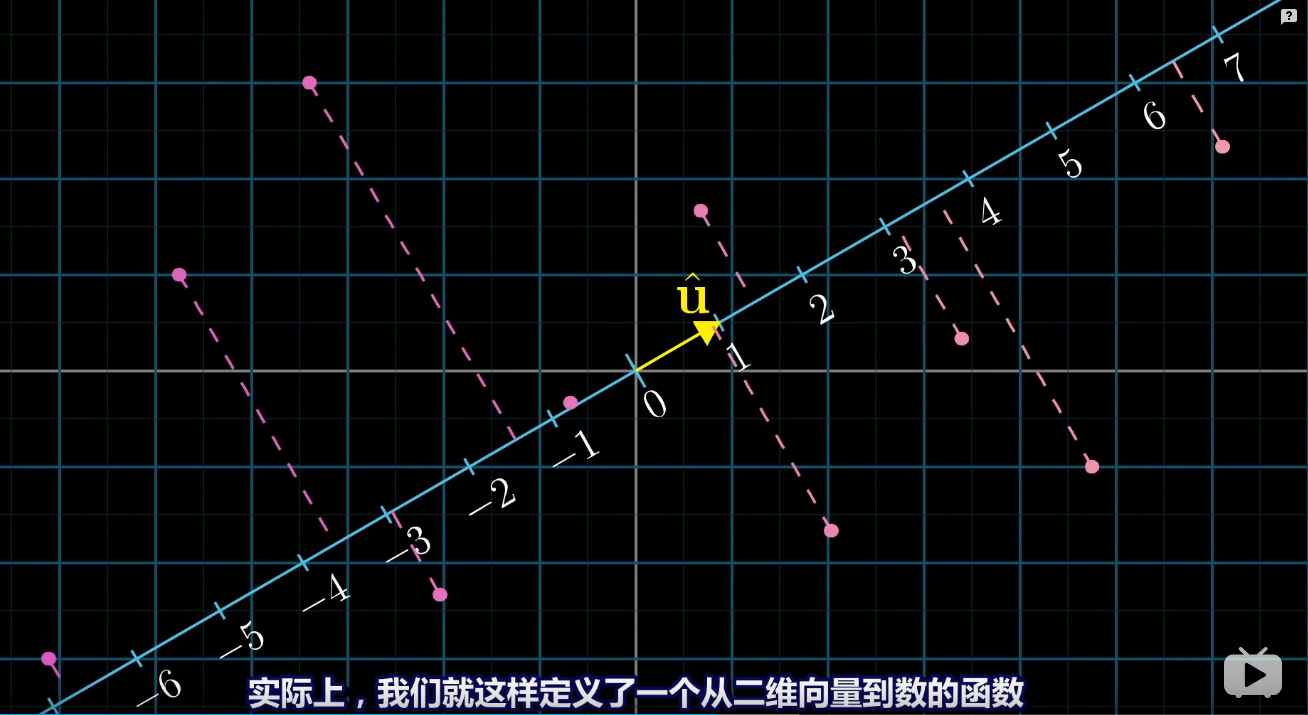
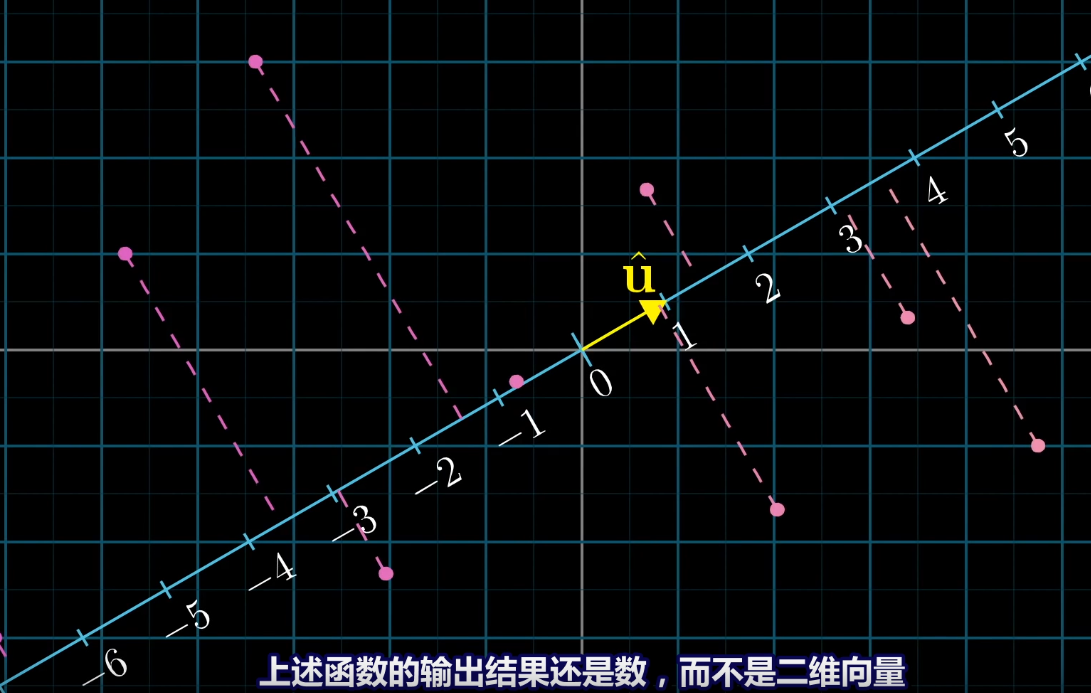
基向量u的坐標為[ux uy] , ux與uy也是基向量i與基向量j投影在基向量上的值(根據作圖,對偶性可證)。
i與u的點積=ux*1(基向量u的長度)=ux, j與u的點積=uy*1(基向量u的長度) , ux+uy 等于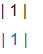 * (基向量u),根據下圖的原則 :
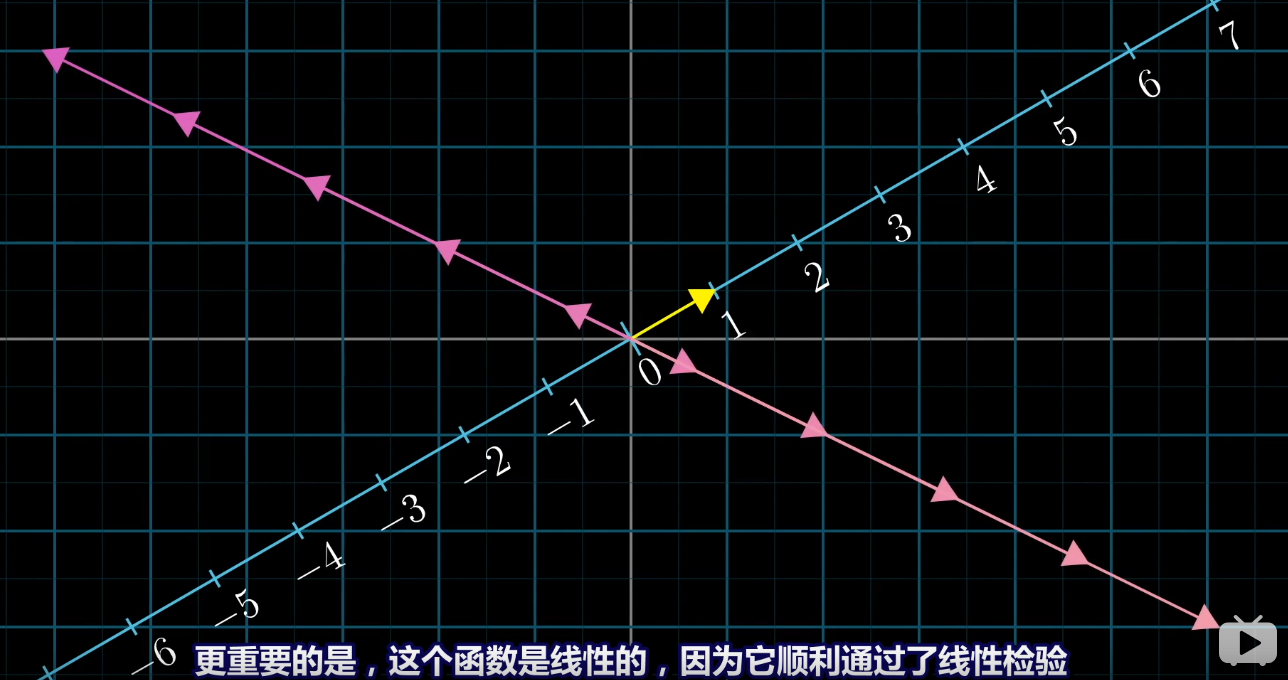
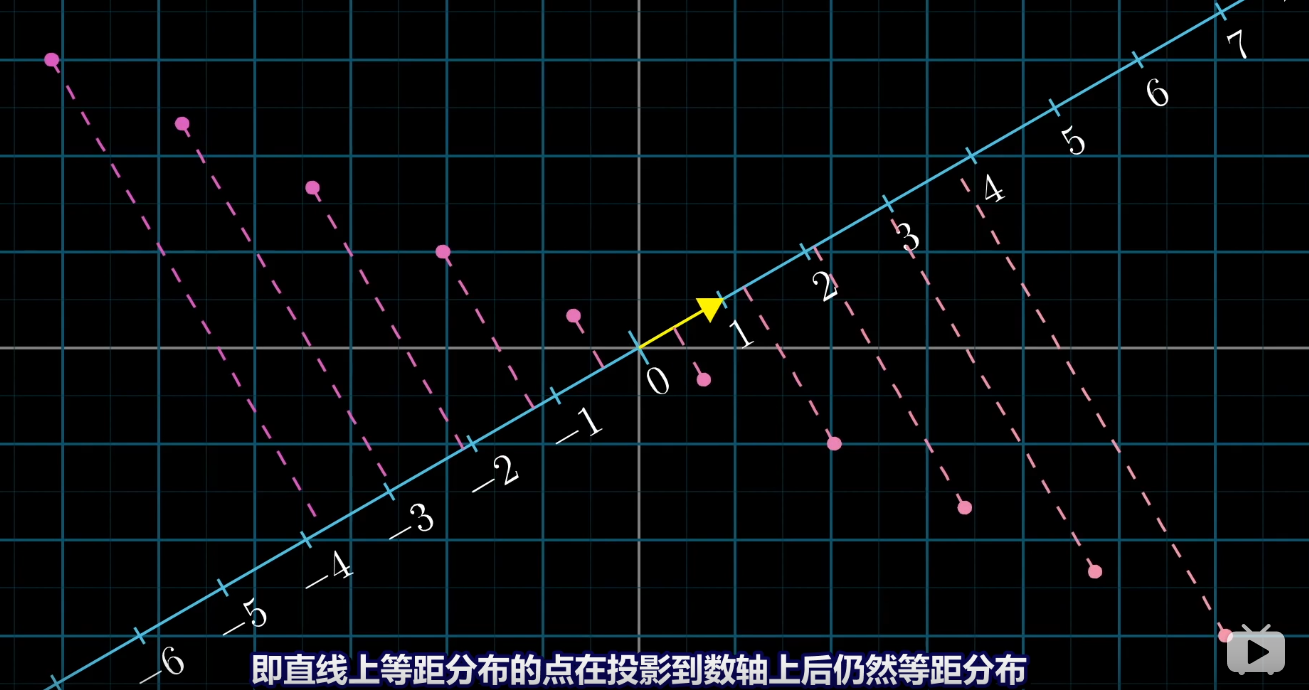
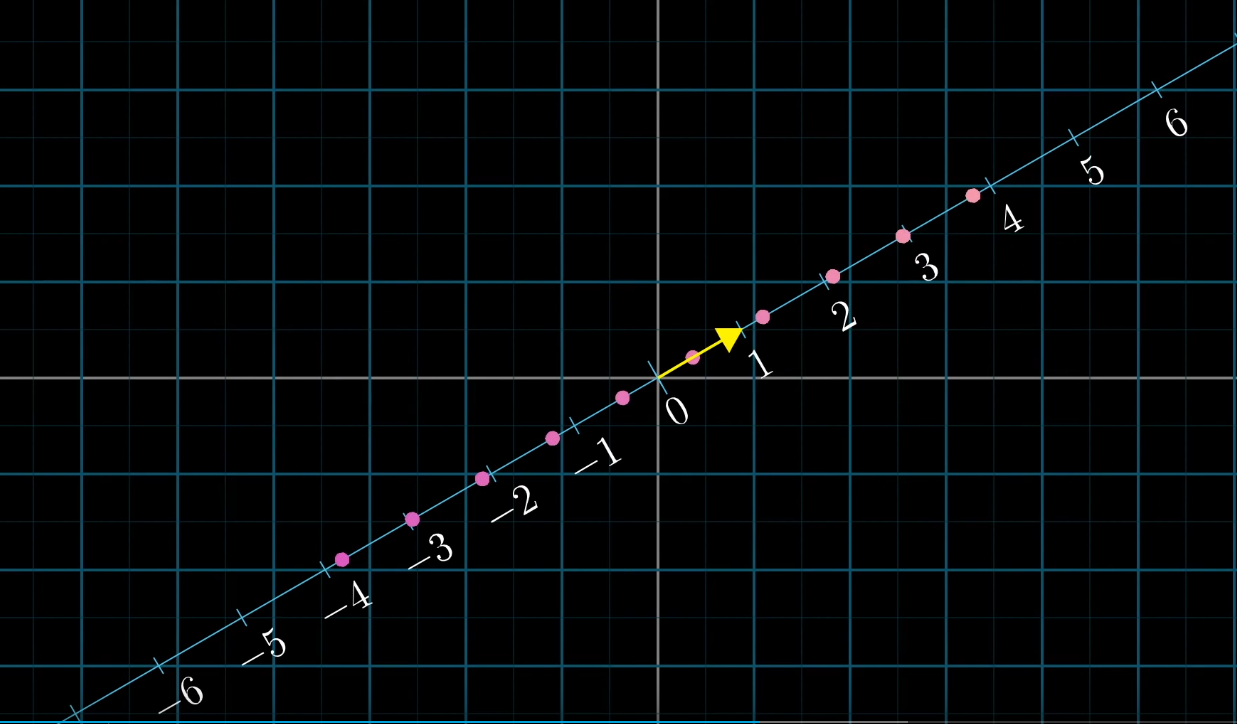
**1.投影是線性的變換**

**2. 一個向量的線性變換與它分量變換的和相同**
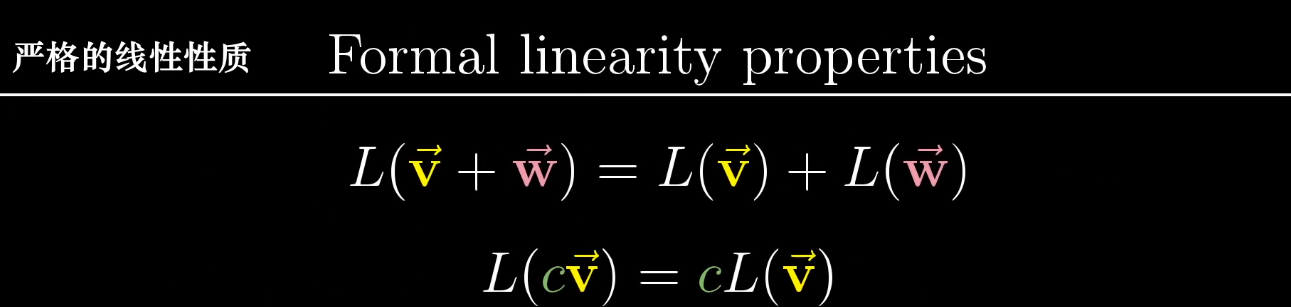
**向量相等,長度一樣,方向一樣**
*****
任一一向量v 都可以看做n*u(這個向量方向上的基向量),坐標為(n*ux,n*uy)。ux和uy為二維基向量i和j的投影。 [n*ux , n*ny] * 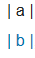 , 那么向量 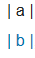 在 向量v上投影后的數值為=》a*ux*n+b*uy*n,所以