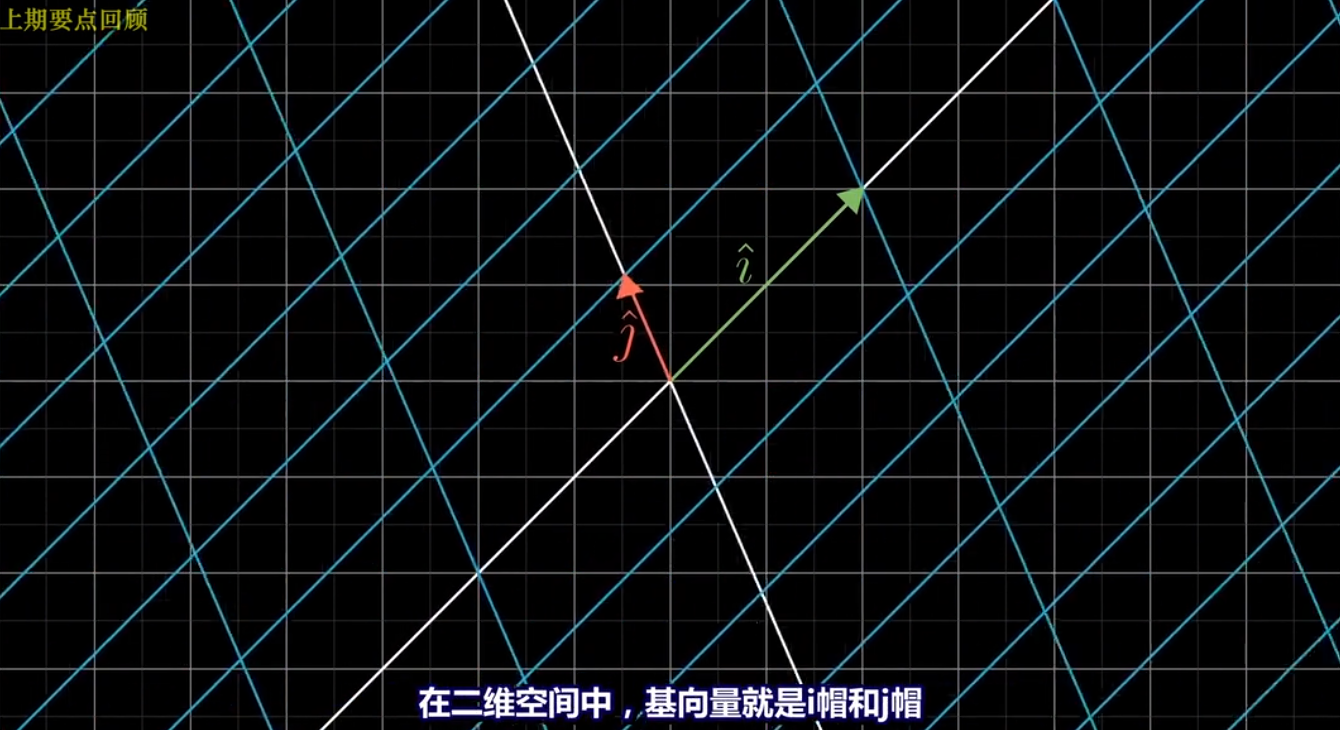
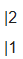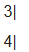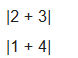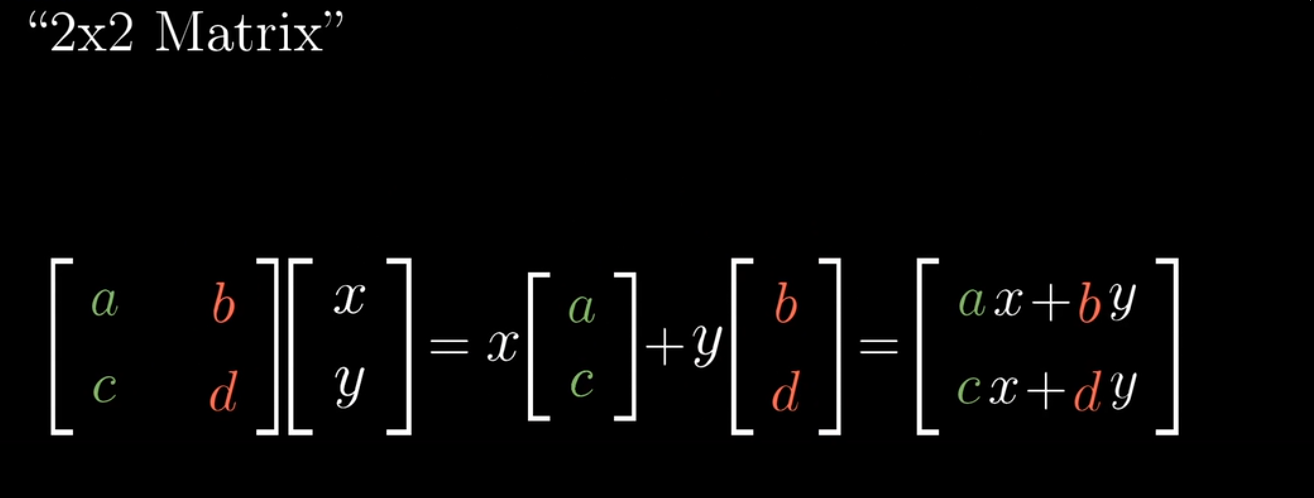
線性變換可以通過基向量決定，如下圖：  ***** **對2*2矩陣的理解** |2 + 3| |1 + 4| 這個2*2矩陣可以看做包含了一個線性變換信息， 是線性變換后 i 向量在原坐標系上的坐標,i向量坐標為（2，1)。 是線性變換后 j 向量在原坐標席上的坐標，j向量坐標為(3,4) *****  包含了兩個向量，左邊一個，右邊一個。將兩個向量相加得到一個 在原坐標系中新的向量  ==》 *****  一個給定向量經過線性變換后得到變換后的新向量 ***** **兩矩陣相乘的意義** 兩個2*2矩陣相乘，表示先進行右邊矩陣的變換，再進行左邊矩陣的變換，最后結果生成一個2*2矩陣表示復合變換。  ***** **求解復合變換的矩陣** 新的復合變換矩陣含有新的變換后i的信息和變換后j的信息。 1.先將第一個變換的**i**進行第二次變換，得到新的變換后的**i**，是復合矩陣的**i** 。  2.在將第一個變換的**j**進行第二次變換，得到新的變換后的**j**，是復合矩陣的**j**。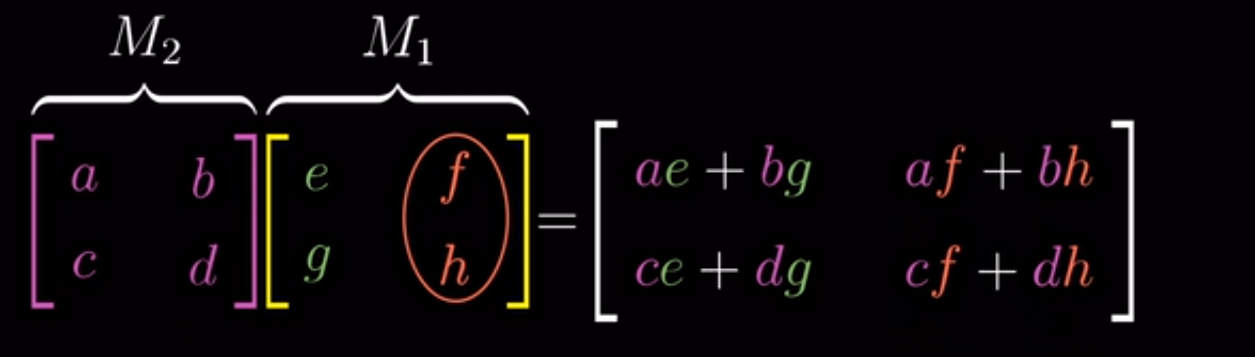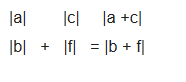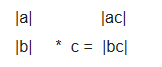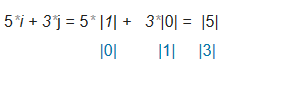  ***** **向量加法**  **向量數乘**  ***** 如下圖一個向量的坐標也是通過基向量得到該向量的線性組合的標量序列  ***** 線性變換的順序不同，最后復合變換的也結果不同。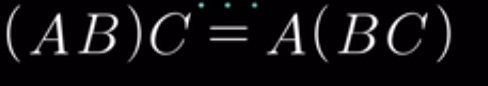線性變換從右邊開始 M1M2 ≠ M2M1 ***** **線性變換結合律**  因為線性變換從右邊開始，都是先C變換，再B變換，再A變換