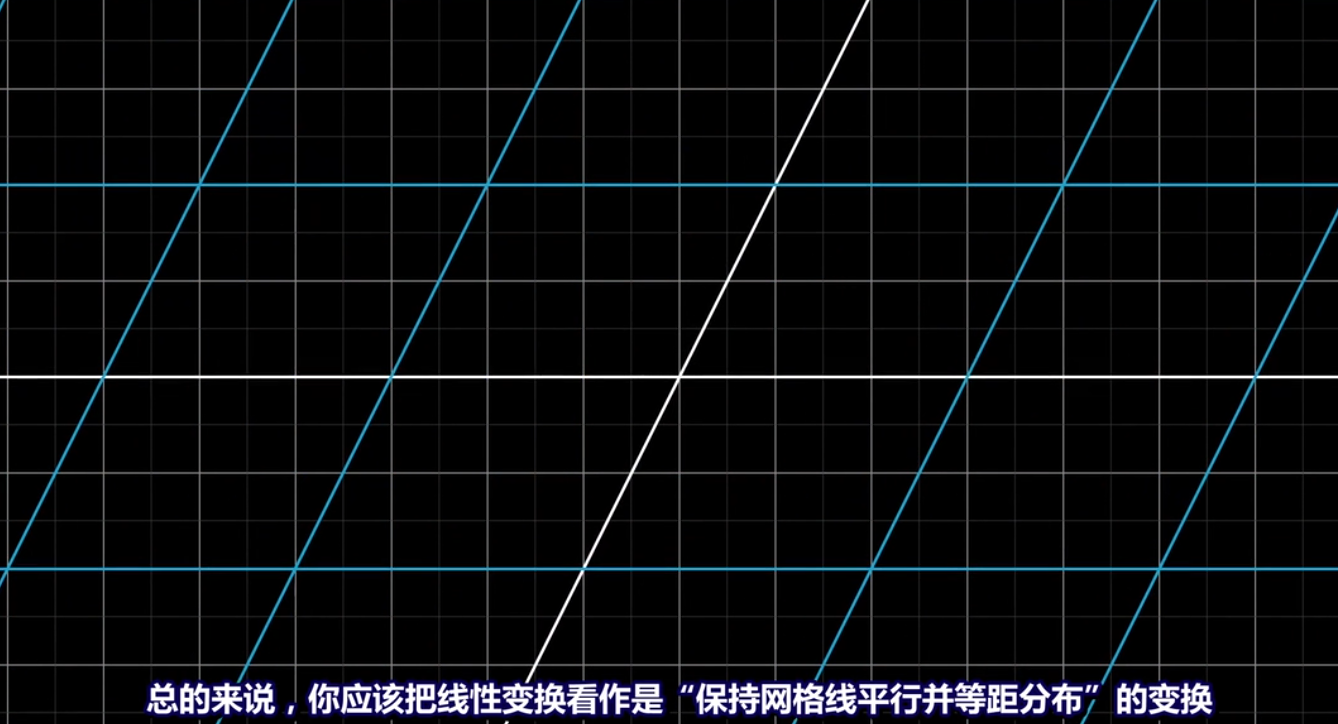
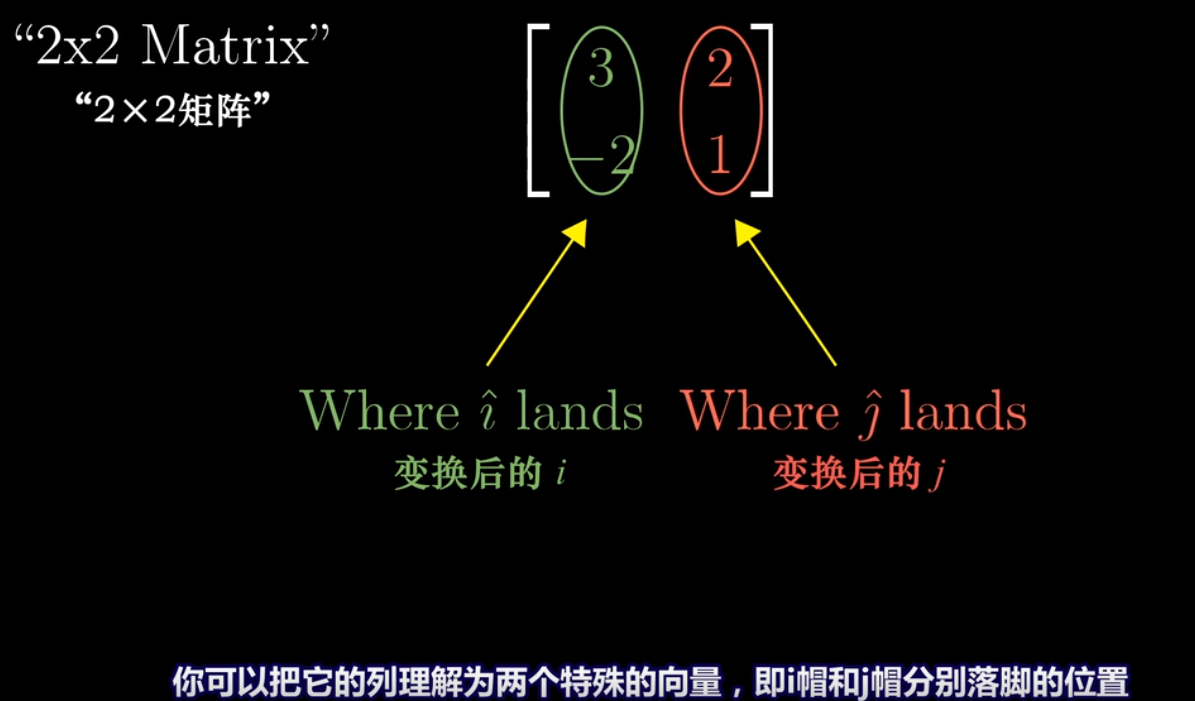
線性變換是函數的一種說法。 在原坐標系中，任一向量都可以通過基向量的某種線性組合來得到。 **變換**暗示以特定方式可視覺化這一輸入-輸出關系。 **線性變換特點**：1.一條直線變換后仍為直線 2.原點保持固定 **線性變換解釋**:先對基向量i的坐標進行移動，使 i 向量所在直線和其他平形直線同時進行旋轉和縮放。i 向量所在直線原點不變。再對基向量j的坐標進行移動，使 j 向量所在直線和其他平形直線同時進行旋轉和縮放。j 向量所在直線原點不變。  ***** **對原坐標系中向量的理解** i 向量坐標[ 1 0] j向量坐標[0 1] ,在原坐標系中。[3 -5]既是一個向量，也可以看作 3i + (-5j)這個特定線性組合中的標量數字序列 ***** **用數值描述線性變換 2*2矩陣和1*2矩陣相乘的幾何意義** 一個線性變換可以通過記錄兩個基向量 i 和 j 變換后坐標來描述這種變換。2*2矩陣表示二維坐標的變換信息  ***** 對于原坐標系中一個給定向量，是基向量的特定線性組合v = ai +b j。對坐標系變換后，求變換后向量的坐標，v(變換后)= a*(變換后的i) + b* (變換后的j)  用數學公式表達如下圖： 下圖式子的含義，（經過變換后的基向量i j）* (線性組合的標量數字序列) = 得到（變換后的基向量通過線性組合生成的新向量。新向量用2*2矩陣表示，左邊是x*(變換后的i),右邊是y*（變換后的j）  *****