*****
### 引入
如果 a+b+c=1000,且 a^2+b^2=c^2(a,b,c 為自然數),如何求出所有a、b、c可能的組合?
代碼實現
```
import time
start_time = time.time()
for a in range(0, 1001):
for b in range(0, 1001):
for c in range(0, 1001):
if a**2 + b**2 == c**2 and a+b+c == 1000:
print("a, b, c: %d, %d, %d" % (a, b, c))
end_time = time.time()
print("times: %f" % (end_time - start_time))
print("end!")
```
### 算法的概念
算法是計算機處理信息的本質,因為計算機程序本質上是一個算法來告訴計算機確切的步驟來執行一個指定的任務。一般地,當算法在處理信息時,會從輸入設備或數據的存儲地址讀取數據,把結果寫入輸出設備或某個存儲地址供以后再調用。
算法是獨立存在的一種解決問題的方法和思想。
對于算法而言,實現的語言并不重要,重要的是思想。
算法可以有不同的語言描述實現版本(如C描述、C++描述、Python描述等),我們現在是在用Python語言進行描述實現。
### 算法的五大特性
- 輸入: 算法具有0個或多個輸入
- 輸出: 算法至少有1個或多個輸出
- 有窮性: 算法在有限的步驟之后會自動結束而不會無限循環,并且每一個步驟可以在可接受的時間內完成
- 確定性:算法中的每一步都有確定的含義,不會出現二義性
- 可行性:算法的每一步都是可行的,也就是說每一步都能夠執行有限的次數完成
### 第二次嘗試
```
import time
start_time = time.time()
for a in range(0, 1001):
for b in range(0, 1001-a):
c = 1000 - a - b
if a**2 + b**2 == c**2:
print("a, b, c: %d, %d, %d" % (a, b, c))
end_time = time.time()
print("times: %f" % (end_time - start_time))
print("complete!")
```
## 算法效率衡量
### 執行時間反應算法效率
對于同一問題,我們給出了兩種解決算法,在兩種算法的實現中,我們對程序執行的時間進行了測算,發現兩段程序執行的時間相差懸殊(214.583347秒相比于0.182897秒),由此我們可以得出結論:實現算法程序的執行時間可以反應出算法的效率,即算法的優劣。
<br>單靠時間值絕對可信嗎?
#### 1.測試結果非常依賴測試環境
測試環境中硬件的不同會對測試結果有很大的影響。比如,我們拿同樣一段代碼,分別用 Intel Core i9 處理器和 Intel Core i3 處理器來運行,不用說,i9 處理器要比 i3 處理器執行的速度快很多。還有,比如原本在這臺機器上 a 代碼執行的速度比 b 代碼要快,等我們換到另一臺機器上時,可能會有截然相反的結果。
#### 2.測試結果受數據規模的影響很大
對同一個排序算法,待排序數據的有序度不一樣,排序的執行時間就會有很大的差別。極端情況下,如果數據已經是有序的,那排序算法不需要做任何操作,執行時間就會非常短。除此之外,如果測試數據規模太小,測試結果可能無法真實地反應算法的性能。
所以,我們需要一個不用具體的測試數據來測試,就可以粗略地估計算法的執行效率的方法
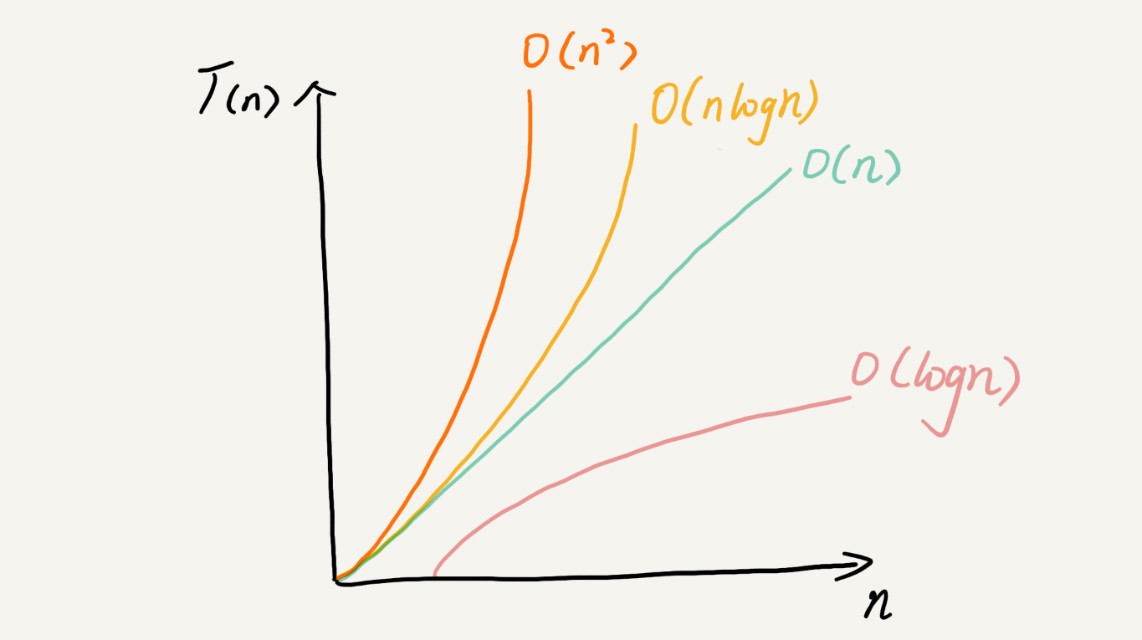
### 大 O 復雜度表示法
算法的執行效率,粗略地講,就是算法代碼執行的時間。但是,如何在不運行代碼的情況下,用“肉眼”得到一段代碼的執行時間呢?
```
for a in range(0, 1001):
for b in range(0, 1001):
for c in range(0, 1001):
if a**2 + b**2 == c**2 and a+b+c == 1000:
print("a, b, c: %d, %d, %d" % (a, b, c))
```
通過這段代碼執行時間的推導過程,我們可以得到一個非常重要的規律,那就是,所有代碼的執行時間 T(n) 與每行代碼的執行次數 n 成正比。
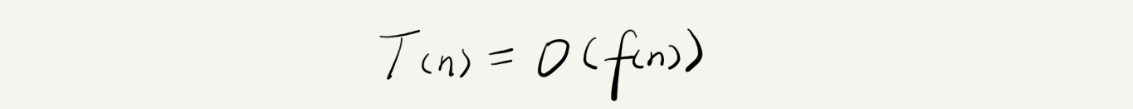
<br>其中,T(n) 我們已經講過了,它表示代碼執行的時間;n 表示數據規模的大小;f(n) 表示每行代碼執行的次數總和。因為這是一個公式,所以用 f(n) 來表示。公式中的 O,表示代碼的執行時間 T(n) 與 f(n) 表達式成正比。
<br>`T(n) = O(n^3*2)`這就是大 O 時間復雜度表示法,大 O 時間復雜度實際上并不具體表示代碼真正的執行時間,而是表示代碼執行時間隨數據規模增長的變化趨勢,所以,也叫作漸進時間復雜度(asymptotic time complexity),簡稱時間復雜度。
<br>當n很大時,你可以把它想象成 10000、100000。而公式中的低階、常量、系數三部分并不左右增長趨勢,所以都可以忽略。我們只需要記錄一個最大量級就可以了
## 時間復雜度分析
### 1.只關注循環執行次數最多的一段代碼
大 O 這種復雜度表示方法只是表示一種變化趨勢。我們通常會忽略掉公式中的常量、低階、系數,只需要記錄一個最大階的量級就可以了。所以,我們在分析一個算法、一段代碼的時間復雜度的時候,也只關注循環執行次數最多的那一段代碼就可以了。這段核心代碼執行次數的 n 的量級,就是整段要分析代碼的時間復雜度。
```
def cal(n):
sum = 0
i = 1
for i in rang(n+1):
sum += i
i+=1
return sum
```
其中第 2、3 行代碼都是常量級的執行時間,與 n 的大小無關,所以對于復雜度并沒有影響。循環執行次數最多的是第 4、5 行代碼,所以這塊代碼要重點分析。前面我們也講過,這兩行代碼被執行了 n 次,所以總的時間復雜度就是 O(n)。
### 2.加法法則:總復雜度等于量級最大的那段代碼的復雜度
```
def cal(n):
sum = 0
i = 1
for in range(100):
sum += i
for i in rang(n+1):
sum += i
i+=1
for i in range(n+1):
for j in range(n+1):
pass
```
綜合這三段代碼的時間復雜度,我們取其中最大的量級。所以,整段代碼的時間復雜度就為 O(n2)。也就是說:總的時間復雜度就等于量級最大的那段代碼的時間復雜度
### 最壞時間復雜度
分析算法時,存在幾種可能的考慮:
- 算法完成工作最少需要多少基本操作,即最優時間復雜度
- 算法完成工作最多需要多少基本操作,即最壞時間復雜度
- 算法完成工作平均需要多少基本操作,即平均時間復雜度
對于列表排序,要查找的變量 x 可能出現在數組的任意位置。如果數組中第一個元素正好是要查找的變量 x,那就不需要繼續遍歷剩下的 n-1 個數據了,那時間復雜度就是 O(1)。但如果數組中不存在變量 x,那我們就需要把整個數組都遍歷一遍,時間復雜度就成了 O(n)。所以,不同的情況下,這段代碼的時間復雜度是不一樣的。
對于最優時間復雜度,其價值不大,因為它沒有提供什么有用信息,其反映的只是最樂觀最理想的情況,沒有參考價值。
對于最壞時間復雜度,提供了一種保證,表明算法在此種程度的基本操作中一定能完成工作。
對于平均時間復雜度,是對算法的一個全面評價,因此它完整全面的反映了這個算法的性質。但另一方面,這種衡量并沒有保證,不是每個計算都能在這個基本操作內完成。而且,對于平均情況的計算,也會因為應用算法的實例分布可能并不均勻而難以計算。
因此,我們主要關注算法的最壞情況,亦即最壞時間復雜度。
### 常見時間復雜度
常見的復雜度并不多,從低階到高階有:O(1)、O(logn)、O(n)、O(nlogn)、O(n2)。
執行次數函數舉例 | 階 | 非正式術語
---|---|---|
12 | O(1) |常數階
2n + 3 | O(n) | 線性階
3n^2 + 3n + 1| O(n^2)| 平方階
log2n + 20|O(logn)| 對數階
2n+3nlog2n+19|O(nlogn)|nlogn階
2^n|O(2^n)|指數階