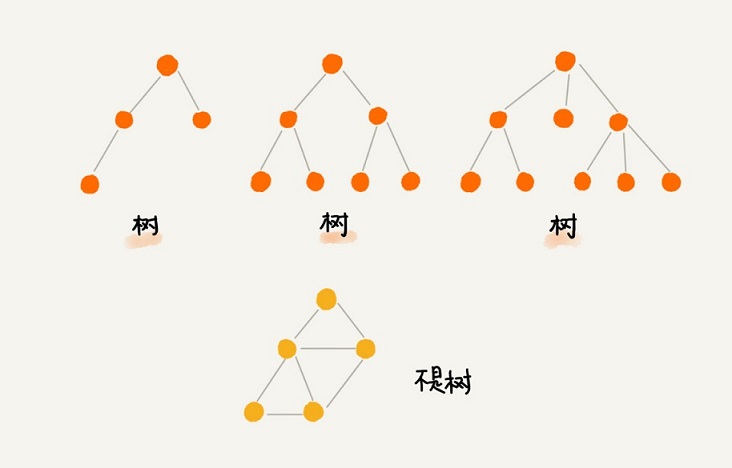
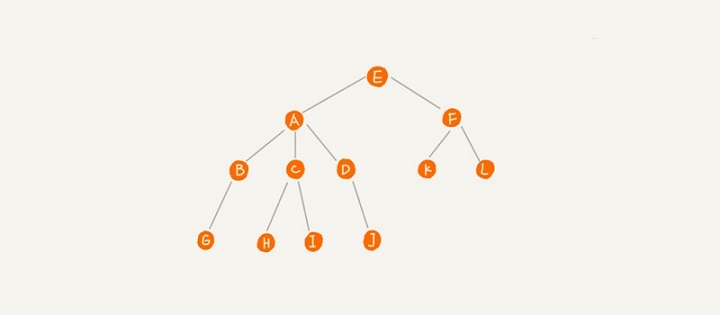
***** ## 樹的概念 樹（英語：tree）是一種抽象數據類型（ADT）或是實作這種抽象數據類型的數據結構，用來模擬具有樹狀結構性質的數據集合。它是由n（n>=1）個有限節點組成一個具有層次關系的集合。把它叫做“樹”是因為它看起來像一棵倒掛的樹，也就是說它是根朝上，而葉朝下的。它具有以下的特點： - 每個節點有零個或多個子節點； - 沒有父節點的節點稱為根節點； - 每一個非根節點有且只有一個父節點； - 除了根節點外，每個子節點可以分為多個不相交的子樹；  你有沒有發現，“樹”這種數據結構真的很像我們現實生活中的“樹”，這里面每個元素我們叫作“節點”；用來連線相鄰節點之間的關系，我們叫作“父子關系”。  A 節點就是 B 節點的**父節點**，B 節點是 A 節點的**子節點**。B、C、D 這三個節點的父節點是同一個節點，所以它們之間互稱為**兄弟節點**。我們把沒有父節點的節點叫作**根節點**，也就是圖中的節點 E。我們把沒有子節點的節點叫作**葉子節點**或者**葉節點**，比如圖中的 G、H、I、J、K、L 都是葉子節點。 <br>除此之外，關于“樹”，還有三個比較相似的概念：**高度**（Height）、**深度**（Depth）、**層**（Level）。它們的定義是這樣的 * 節點的高度:節點到葉子節點的最長路徑 * 節點的深度:根節點到這個節點所經歷的邊的個數 * 節點的層數:節點的深度+1 * 樹的高度:根節點的高度 這三個概念的定義比較容易混淆，描述起來也比較空洞。我舉個例子說明一下，你一看應該就能明白。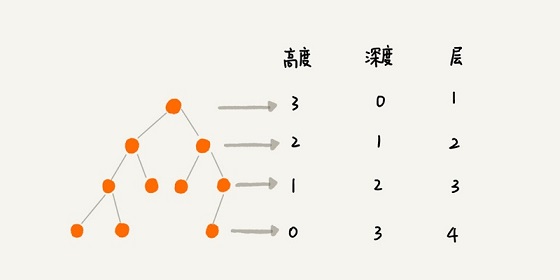  ### 樹的種類 * 無序樹：樹中任意節點的子節點之間沒有順序關系，這種樹稱為無序樹，也稱為自由樹； * 有序樹：樹中任意節點的子節點之間有順序關系，這種樹稱為有序樹； * 二叉樹：每個節點最多含有兩個子樹的樹稱為二叉樹； * 完全二叉樹：對于一顆二叉樹，假設其深度為d(d>1)。除了第d層外，其它各層的節點數目均已達最大值，且第d層所有節點從左向右連續地緊密排列，這樣的二叉樹被稱為完全二叉樹，其中滿二叉樹的定義是所有葉節點都在最底層的完全二叉樹; * 平衡二叉樹（AVL樹）：當且僅當任何節點的兩棵子樹的高度差不大于1的二叉樹； * 排序二叉樹（二叉查找樹（英語：Binary Search Tree），也稱二叉搜索樹、有序二叉樹）； * 霍夫曼樹（用于信息編碼）：帶權路徑最短的二叉樹稱為哈夫曼樹或最優二叉樹； * B樹：一種對讀寫操作進行優化的自平衡的二叉查找樹，能夠保持數據有序，擁有多余兩個子樹。 ### 二叉樹 二叉樹，顧名思義，每個節點最多有兩個“叉”，也就是兩個子節點，分別是左子節點和右子節點。不過，二叉樹并不要求每個節點都有兩個子節點，有的節點只有左子節點，有的節點只有右子節點。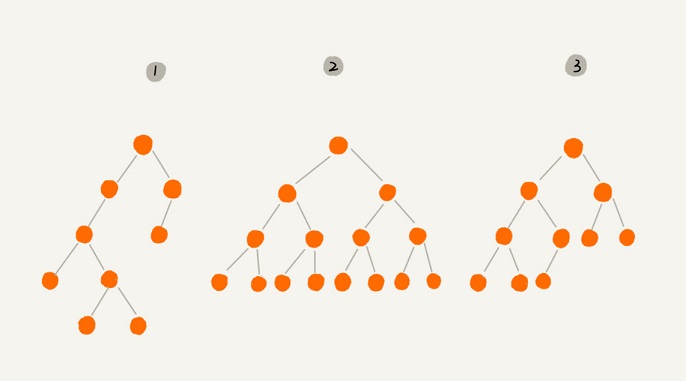  這個圖里面，有兩個比較特殊的二叉樹，分別是編號 2 和編號 3 這兩個。 <br>其中，編號 2 的二叉樹中，葉子節點全都在最底層，除了葉子節點之外，每個節點都有左右兩個子節點，這種二叉樹就叫作**滿二叉樹。** <br>編號 3 的二叉樹中，葉子節點都在最底下兩層，最后一層的葉子節點都靠左排列，并且除了最后一層，其他層的節點個數都要達到最大，這種二叉樹叫作**完全二叉樹。** <br>二叉排序樹:[https://baike.baidu.com/item/二叉排序樹/10905079?fr=aladdin](https://baike.baidu.com/item/%E4%BA%8C%E5%8F%89%E6%8E%92%E5%BA%8F%E6%A0%91/10905079?fr=aladdin) ### 樹的存儲與表示 順序存儲：將數據結構存儲在固定的數組中，然在遍歷速度上有一定的優勢，但因所占空間比較大，是非主流二叉樹。二叉樹通常以鏈式存儲。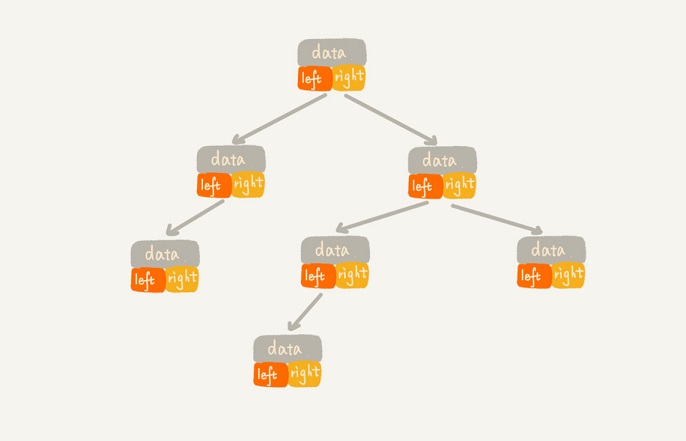  鏈式存儲：  從圖中你應該可以很清楚地看到，每個節點有三個字段，其中一個存儲數據，另外兩個是指向左右子節點的指針。我們只要拎住根節點，就可以通過左右子節點的指針，把整棵樹都串起來。這種存儲方式我們比較常用。大部分二叉樹代碼都是通過這種結構來實現的。 ### 常見的一些樹的應用場景 1. xml，html等，那么編寫這些東西的解析器的時候，不可避免用到樹 2. 路由協議就是使用了樹的算法 3. mysql數據庫索引 4. 文件系統的目錄結構 5. 所以很多經典的AI算法其實都是樹搜索，此外機器學習中的decision tree也是樹結構