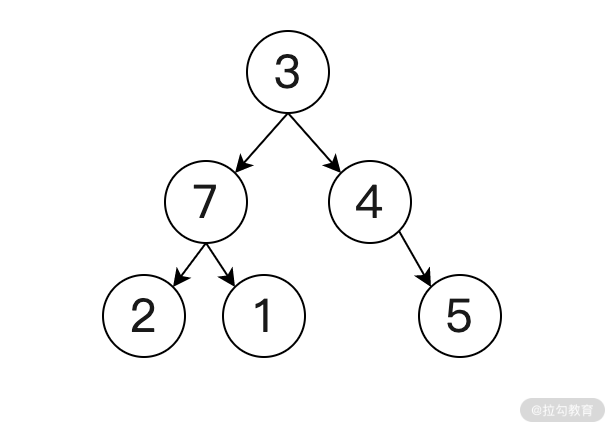
數據結構屬于理解一些源碼和技術所必備的知識，比如要讀懂 Java 語言中 TreeMap 和 TreeSet 的源碼就要懂紅黑樹的數據結構，不然是無法理解源碼中關于紅黑樹數據的操作代碼的，比如左旋、右旋、添加和刪除操作等。因此本課時我們就來學習一下數據結構的基礎知識，方便看懂源碼或者是防止面試中被問到。 我們本課時的面試題是，紅黑樹和二叉樹有什么區別？ #### 典型回答 要回答這個問題之前，我們先要弄清什么是二叉樹？什么是紅黑樹？ 二叉樹（Binary Tree）是指每個節點最多只有兩個分支的樹結構，即不存在分支大于 2 的節點，二叉樹的數據結構如下圖所示：  這是一棵擁有 6 個節點深度為 2（深度從 0 開始），并且根節點為 3 的二叉樹。 二叉樹有兩個分支通常被稱作“左子樹”和“右子樹”，而且這些分支具有左右次序不能隨意地顛倒。 一棵空樹或者滿足以下性質的二叉樹被稱之為二叉查找樹： * 若任意節點的左子樹不為空，則左子樹上所有節點的值均小于它的根節點的值； * 若任意節點的右子樹不為空，則右子樹上所有節點的值均大于或等于它的根節點的值； * 任意節點的左、右子樹分別為二叉查找樹。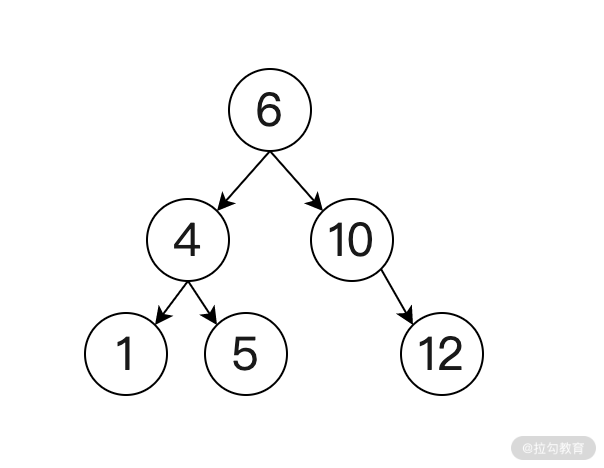 如下圖所示，這就是一個標準的二叉查找樹：  二叉查找樹（Binary Search Tree）也被稱為二叉搜索樹、有序二叉樹（Ordered Binary Tree）或排序二叉樹（Sorted Binary Tree）等。 紅黑樹（Red Black Tree）是一種自平衡二叉查找樹，它最早被稱之為“對稱二叉 B 樹”，它現在的名字源于 1978 年的一篇論文，之后便被稱之為紅黑樹了。 所謂的平衡樹是指一種改進的二叉查找樹，顧名思義平衡樹就是將二叉查找樹平衡均勻地分布，這樣的好處就是可以減少二叉查找樹的深度。 一般情況下二叉查找樹的查詢復雜度取決于目標節點到樹根的距離（即深度），當節點的深度普遍較大時，查詢的平均復雜度就會上升，因此為了實現更高效的查詢就有了平衡樹。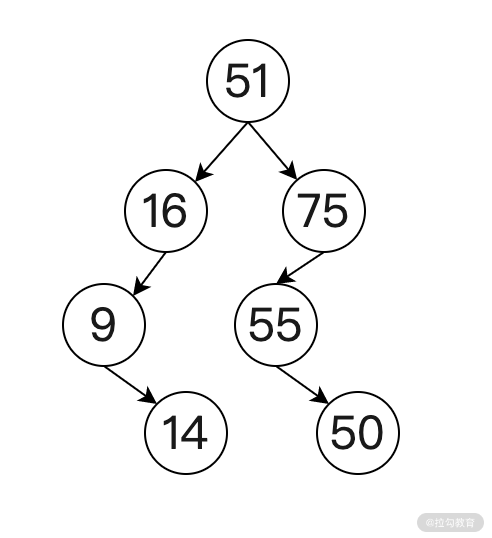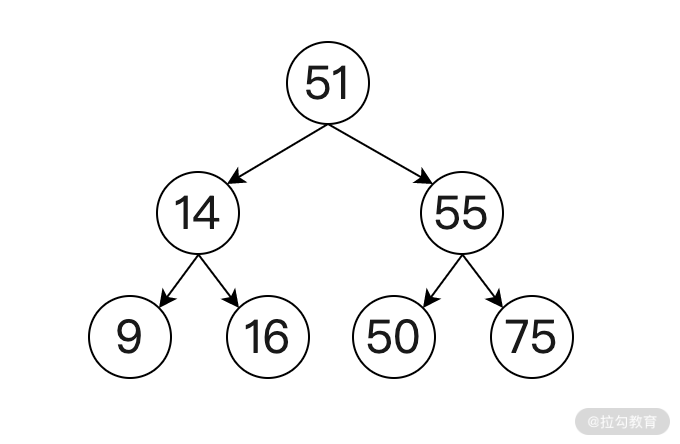 非平衡二叉樹如下圖所示：  平衡二叉樹如下圖所示：  可以看出使用平衡二叉樹可以有效的減少二叉樹的深度，從而提高了查詢的效率。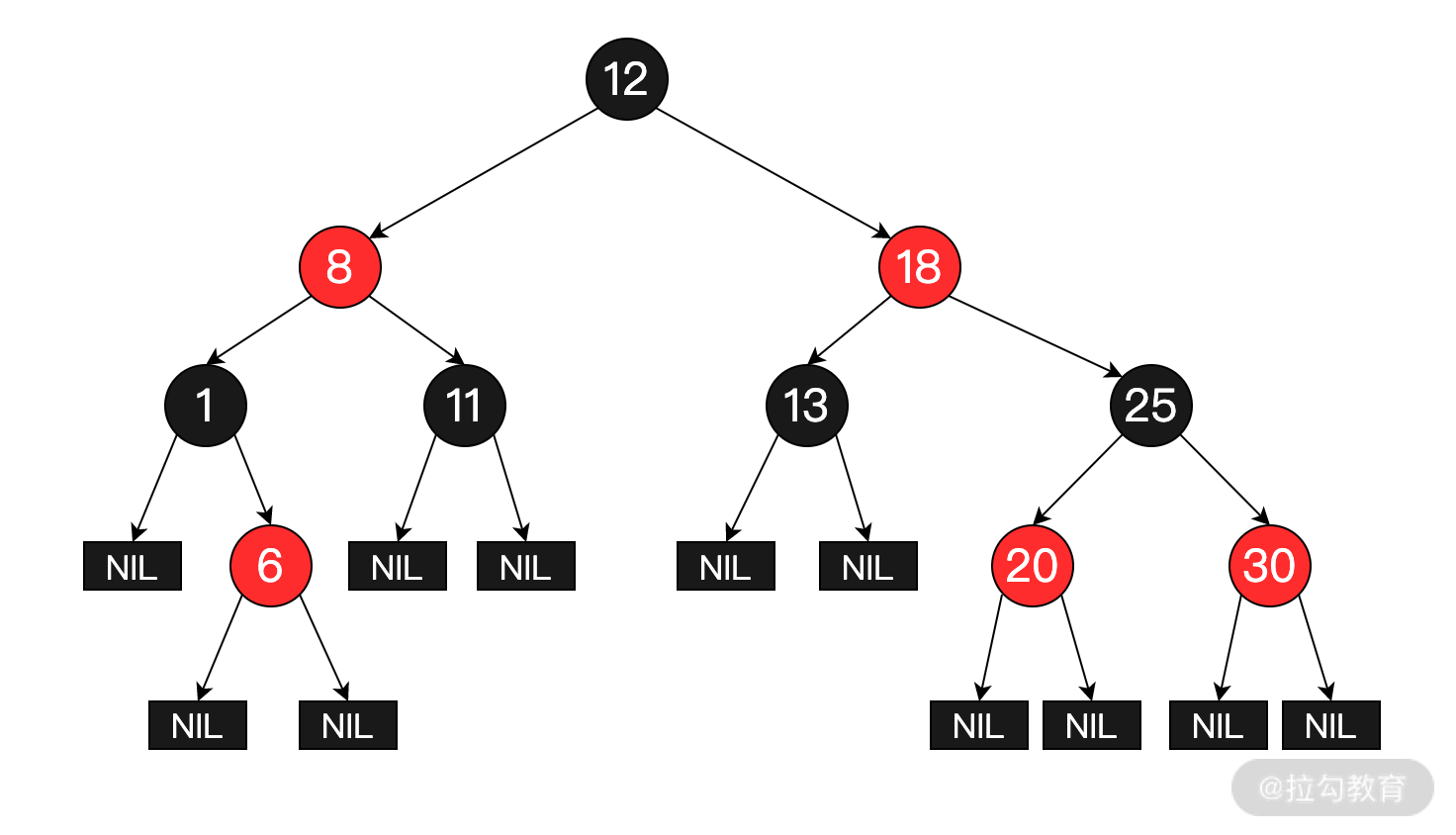 紅黑樹除了具備二叉查找樹的基本特性之外，還具備以下特性： * 節點是紅色或黑色； * 根節點是黑色； * 所有葉子都是黑色的空節點（NIL 節點）； * 每個紅色節點必須有兩個黑色的子節點，也就是說從每個葉子到根的所有路徑上，不能有兩個連續的紅色節點； * 從一個節點到該節點的子孫節點的所有路徑上包含相同數目的黑色節點。 紅黑樹結構如下圖所示：  #### 考點分析 紅黑樹是一個較為復雜的數據結構，尤其是對于增加和刪除操作來說，一般面試官不會讓你直接手寫紅黑樹的具體實現。如果你只有很短的時間準備面試的話，那么我建議你不要死磕這些概念，要學會有的放矢，因為即使你花費很多的時間來背這些概念，一轉眼的功夫就會徹底忘掉，所以你只需要大概地了解其中的一些概念和明白大致的原理就足夠了。 和此知識點相關的面試題還有以下這些： * 為什么工程中喜歡使用紅黑樹而不是其他二叉查找樹？ * 紅黑樹是如何保證自平衡的？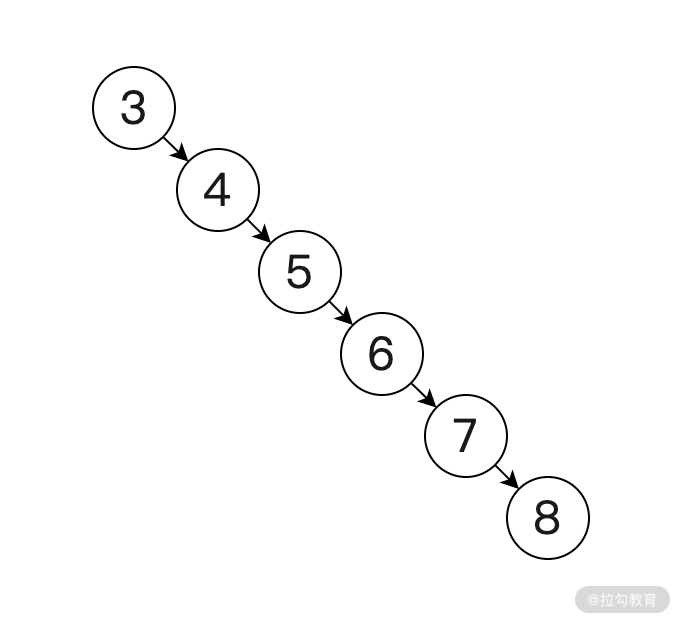 #### 知識擴展 * [ ] 紅黑樹的優勢 紅黑樹的優勢在于它是一個平衡二叉查找樹，對于普通的二叉查找樹（非平衡二叉查找樹）在極端情況下可能會退化為鏈表的結構，例如，當我們依次插入 3、4、5、6、7、8 這些數據時，二叉樹會退化為如下鏈表結構：  當二叉查找樹退化為鏈表數據結構后，再進行元素的添加、刪除以及查詢時，它的時間復雜度就會退化為 O(n)；而如果使用紅黑樹的話，它就會將以上數據轉化為平衡二叉查找樹，這樣就可以更加高效的添加、刪除以及查詢數據了，這就是紅黑樹的優勢。 > 小貼士：紅黑樹的高度近似 log2n，它的添加、刪除以及查詢數據的時間復雜度為 O(logn)。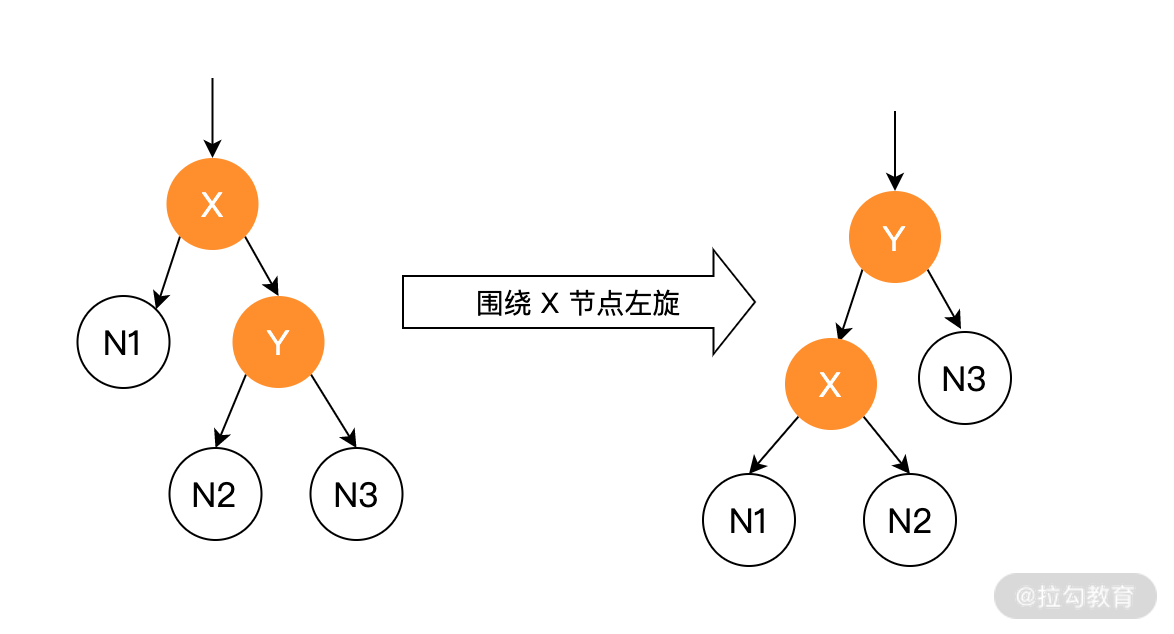 我們在表示算法的執行時間時，通常會使用大 O 表示法，常見的標識類型有以下這些： * O(1)：常量時間，計算時間與數據量大小沒關系； * O(n)：計算時間與數據量成線性正比關系； * O(logn)：計算時間與數據量成對數關系； * [ ] 自平衡的紅黑樹 紅黑樹能夠實現自平衡和保持紅黑樹特征的主要手段是：變色、左旋和右旋。 左旋指的是圍繞某個節點向左旋轉，也就是逆時針旋轉某個節點，使得父節點被自己的右子節點所替代，如下圖所示：  在 TreeMap 源碼中左旋的實現源碼如下： ``` // 源碼基于 JDK 1.8 private void rotateLeft(Entry<K,V> p) { if (p != null) { // 右子節點 Entry<K,V> r = p.right; // p 節點的右子節點為 r 的左子節點 p.right = r.left; // r 左子節點如果非空，r 左子節點的父節點設置為 p 節點 if (r.left != null) r.left.parent = p; r.parent = p.parent; // r 父節點等于 p 父節點 // p 父節點如果為空，那么講根節點設置為 r 節點 if (p.parent == null) root = r; // p 父節點的左子節點如果等于 p 節點，那么 p 父節點的左子節點設置 r 節點 else if (p.parent.left == p) p.parent.left = r; else p.parent.right = r; r.left = p; p.parent = r; } } ``` 左旋代碼說明：在剛開始時，p 為父節點，r 為子節點，在左旋操作后，r 節點代替 p 節點的位置，p 節點成為 r 節點的左孩子，而 r 節點的左孩子成為 p 節點的右孩子。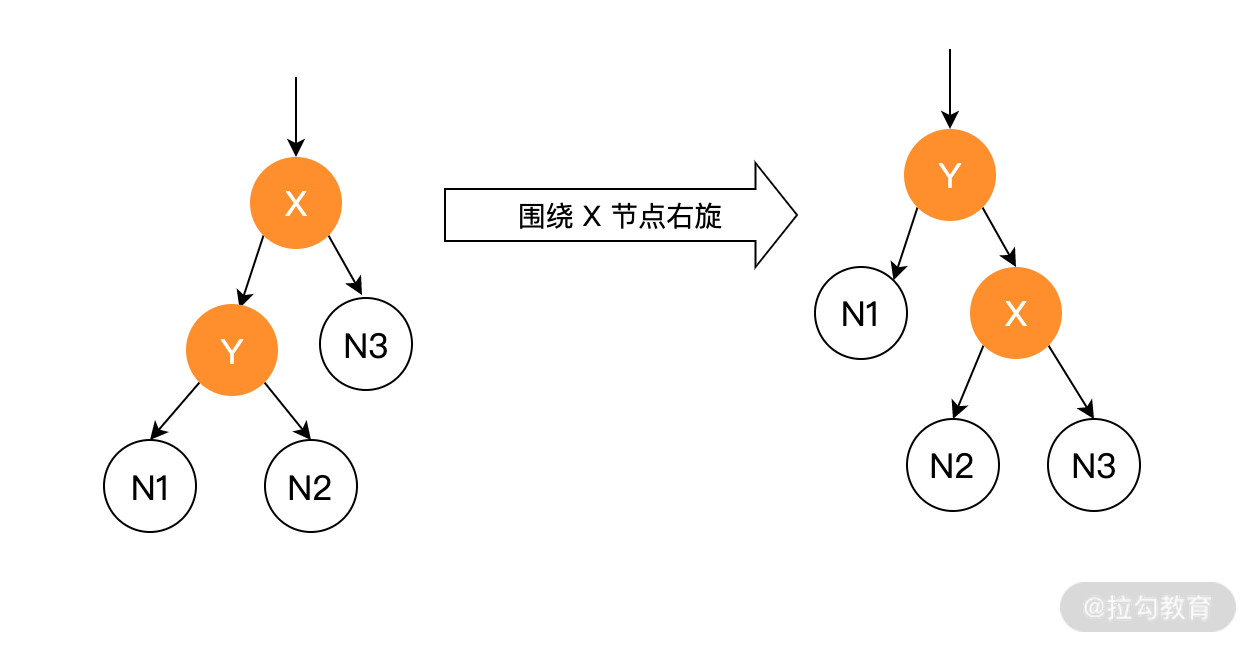 右旋指的是圍繞某個節點向右旋轉，也就是順時針旋轉某個節點，此時父節點會被自己的左子節點取代，如下圖所示：  在 TreeMap 源碼中右旋的實現源碼如下： ``` private void rotateRight(Entry<K,V> p) { if (p != null) { Entry<K,V> l = p.left; // p 節點的左子節點為 l 的右子節點 p.left = l.right; // l 節點的右子節點非空時，設置 l 的右子節點的父節點為 p if (l.right != null) l.right.parent = p; l.parent = p.parent; // p 節點的父節點為空時，根節點設置成 l 節點 if (p.parent == null) root = l; // p 節點的父節點的右子節點等于 p 節點時，p 的父節點的右子節點設置為 l else if (p.parent.right == p) p.parent.right = l; else p.parent.left = l; l.right = p; p.parent = l; } } ``` 右旋代碼說明：在剛開始時，p 為父節點 l 為子節點，在右旋操作后，l 節點代替 p 節點，p 節點成為 l 節點的右孩子，l 節點的右孩子成為 p 節點的左孩子。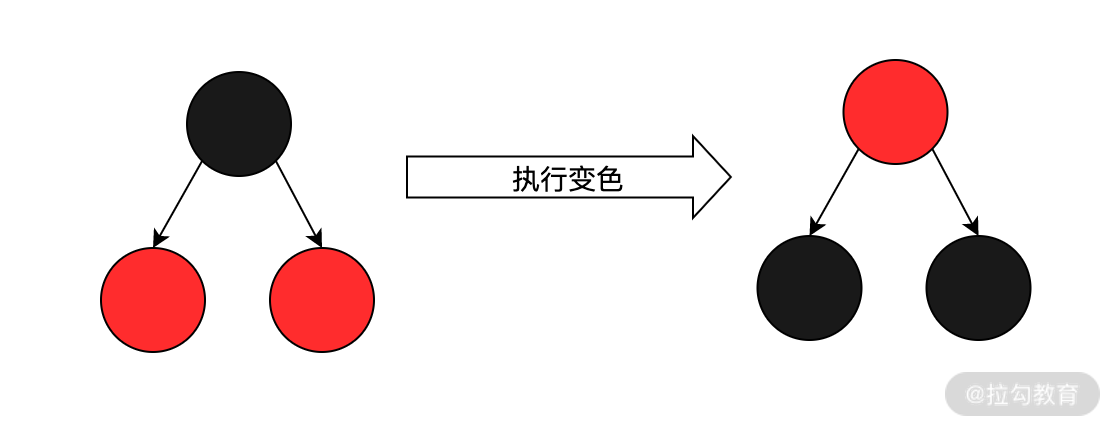 對于紅黑樹來說，如果當前節點的左、右子節點均為紅色時，因為需要滿足紅黑樹定義的第四條特征，所以需要執行變色操作，如下圖所示：  由于篇幅有限，我這里只能帶你簡單地了解一下紅黑樹和二叉樹的基本概念，想要深入地學習更多的內容，推薦查閱《算法》（第四版）和《算法導論》等書籍。 #### 小結 我們本課時介紹了二叉樹、二叉查找樹及紅黑樹的概念，還有紅黑樹的五個特性。普通二叉查找樹在特殊情況下會退化成鏈表的數據結構，因此操作和查詢的時間復雜度變成了 O(n)，而紅黑樹可以實現自平衡，因此它的操作（插入、刪除）和查找的時間復雜度都是 O(logn)，效率更高更穩定，紅黑樹保證平衡的手段有三個：變色、左旋和右旋。 #### 課后問答 * 1、紅黑樹，為什么要有紅色和黑色？2、執行變色操作的目的是？ 講師回復： 紅黑樹本質上是一種平衡樹，執行變色是為了維持節點的平衡。 * 2、紅黑樹的高度最多是 2log（n），這個可以怎么理解？ 講師回復： 紅黑樹的高度取決于節點的個數哦~ * 3、紅黑樹比AVL樹的優點是什么？ 講師回復： AVL屬于早期的平衡樹，紅黑樹可以簡單的理解為包含了 AVL 的特性，同時有新增了顏色的屬性用于存儲更多的信息。