上一課時我們介紹了數據結構的知識，數據結構屬于計算機存儲的基礎，有了它才能更好地將數據進行存儲。而算法可以這樣理解：它是為數據結構服務的，使用合適的算法可以更快地操作和查詢這些數據。 算法的內容有很多，隨隨便便一本算法書有個 700 頁到 1500 頁也是很平常的事，因此我們在這里不能把所有的算法問題全部講到，即使專門再開設一個算法專欄，也只能挑重點的講。那么我們好鋼就要用在刀刃上，本課時會把面試中經常出現的和平常工作中使用頻率最高的算法，拿出來給大家分享。 我們本課時的面試題是，你知道哪些算法？講一下它的內部實現？ #### 典型回答 最常見、最基礎的算法是二分法，它是二分查找算法的簡稱（Binary Search Algorithm），也叫折半搜索算法或對數搜索算法。它是一種在有序數組中查找某一特定元素的搜索算法，顧名思義，是將一組有序元素中的數據劃分為兩組，通過判斷中間值來確認要查找值的大致位置，然后重復此過程進行元素查詢。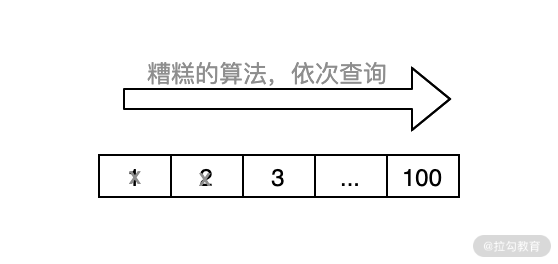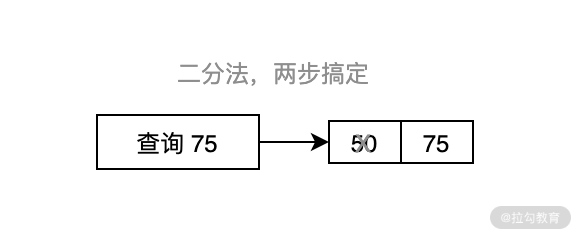 例如，我們要查詢 1~100 中的某個數值，比如我們要查詢的數值為 75，如果按照順序從 1 開始一直往后排序對比的話，需要經歷 75 次，才能查詢到我們想要的數據；而如果使用二分法，則會先判斷 50（1~100 的中間值）和 75 哪個大，然后就能確定要查詢的值是在 50~100 之間，最后再進行二分，用 75 和 75 進行比較，結果發現此值就是我們想要找的那個值，于是我們只用了兩步就找到了要查詢的值，這就是算法的“魔力”。   二分查找算法的實現代碼如下： ``` public class AlgorithmExample { public static void main(String[] args) { // 要查詢的數組 int[] binaryNums = new int[100]; for (int i = 0; i < 100; i++) { // 初始化數組（存入 100 個數據） binaryNums[i] = (i + 1); } // 要查詢的數值 int findValue = 75; // 調用二分查找算法 int binaryResult = binarySearch(binaryNums, 0, binaryNums.length - 1, findValue); // 打印結果 System.out.println("元素的位置是：" + (binaryResult + 1)); } /** * 二分查找算法（返回該值第一次出現的位置） * @param nums 查詢數組 * @param start 開始下標 * @param end 結束下標 * @param findValue 要查找的值 * @return int */ private static int binarySearch(int[] nums, int start, int end, int findValue) { if (start <= end) { // 中間位置 int middle = (start + end) / 2; // 中間的值 int middleValue = nums[middle]; if (findValue == middleValue) { // 等于中值直接返回 return middle; } else if (findValue < middleValue) { // 小于中值，在中值之前的數據中查找 return binarySearch(nums, start, middle - 1, findValue); } else { // 大于中值，在中值之后的數據中查找 return binarySearch(nums, middle + 1, end, findValue); } } return -1; } } ``` 以上程序的執行結果為： ``` 元素的位置是：75 ``` 從上面的內容我們可以看出二分法雖然簡單，但是也要滿足一個特定的條件才行，那就是要使用二分法必須是有序排列的數值才行，不然是沒辦法實現二分法的。 除了二分法之外還有另一個比較常用的排序算法：冒泡排序。 冒泡排序（Bubble Sort）又被稱為泡式排序，它是指重復走訪要排序的數列，每次比較兩個元素，如果順序不對就進行交換，直到沒有被交換的元素為止，這樣就完成了一次冒泡排序。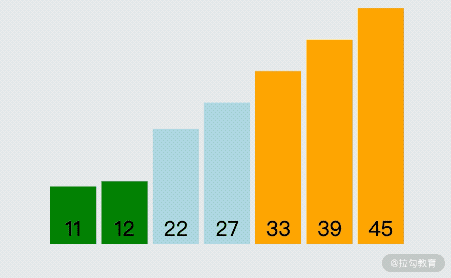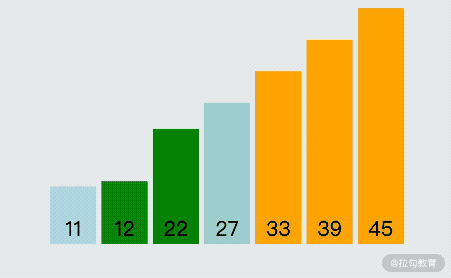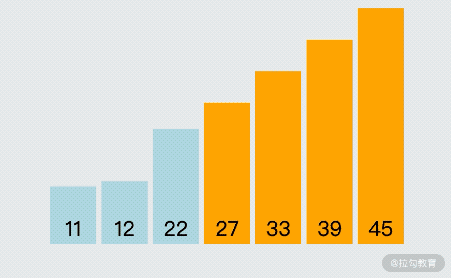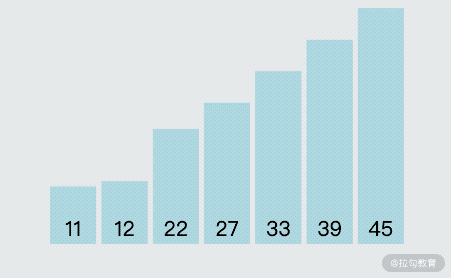 為了讓大家更好地理解冒泡排序，我錄制了一個 gif 圖片用于展示冒泡排序的執行過程，如下圖所示：  由上圖可以看出，冒泡排序的關鍵執行流程是：依次對比相鄰的兩個數字，如果前面的數字大于后面的數字，那么就將前、后兩個數字進行位置交換；這樣每次對比完一輪數據之后，能找出此輪最大的數字并放置到尾部，如此重復，直到沒有可以交換的數據為止，這樣就完成了冒泡排序。 接下來我們就使用 Java 代碼來實現一個冒泡排序算法，實現代碼如下： ``` import java.util.Arrays; public class AlgorithmExample { public static void main(String[] args) { // 待排序數組 int[] nums = {33, 45, 11, 22, 12, 39, 27}; bubbleSort(nums); // 打印排序完數組 System.out.println(Arrays.toString(nums)); } /** * 冒泡排序 */ private static void bubbleSort(int[] nums) { for (int i = 1; i < nums.length; i++) { for (int j = 0; j < nums.length - i; j++) { if (nums[j] > nums[j + 1]) { // 前面數字大于后面的數字，執行位置交換 int temp = nums[j]; nums[j] = nums[j + 1]; nums[j + 1] = temp; } } } } } ``` 以上程序的執行結果為： ``` [11, 12, 22, 27, 33, 39, 45] ``` 從以上結果可以看出，冒泡排序算法的執行成功了，結果也符合我們的預期。 #### 考點分析 冒泡排序和二分法屬于程序員必須掌握的兩種最基礎的算法了，如果連這兩個算法都不知道或者都不能手寫這兩種算法的話，可能會給面試官留下非常不好的印象。因為二者都屬于基礎中的基礎了，其實只要理解了兩種算法的核心思想，再手寫代碼也不是什么難事，如果實在寫不出具體的代碼，最起碼要做到能寫出偽代碼的程度。 和此知識點相關的面試題，還有以下這些： * 如何優化冒泡排序算法？ * 是否還知道更多的算法？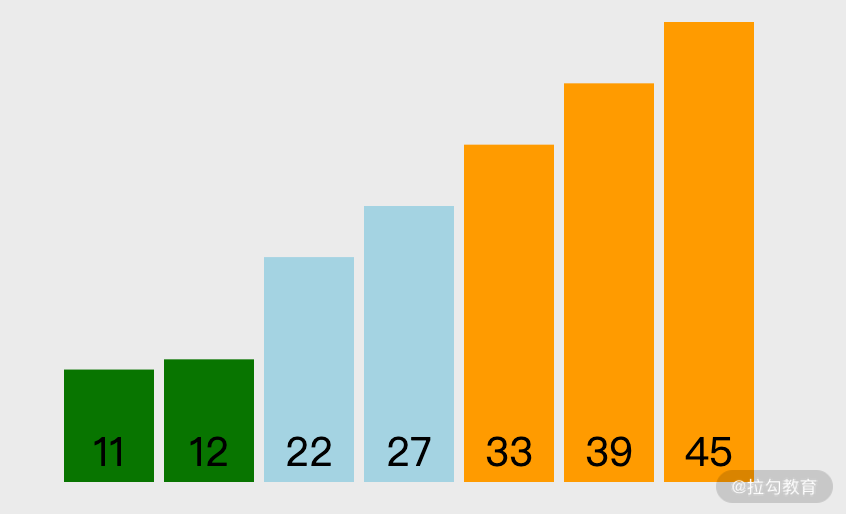 #### 知識擴展 * [ ] 冒泡排序優化 從上面冒泡排序的 gif 圖片可以看出，在最后一輪對比之前，數組的排序如下圖所示：  從圖片可以看出，此時數組已經完全排序好了，但是即使這樣，冒泡排序還是又執行了一次遍歷對比，如下圖所示：  因此我們就可以想辦法去掉無效的遍歷，這樣就可以優化冒泡排序的執行效率了。 我們可以在第一層循環內加一個判斷標識，每次賦值為 true，假如在第二層循環（內層循環）時執行了位置交換，也就是 if 中的代碼之后，我們把此值設置成 false；如果執行完內層循環判斷之后，變量依然為 true，這就說明沒有可以移動的元素了，冒泡排序可以結束執行了，優化后的代碼如下所示： ``` import java.util.Arrays; public class AlgorithmExample { public static void main(String[] args) { // 待排序數組 int[] nums = {33, 45, 11, 22, 12, 39, 27}; bubbleSort(nums); // 打印排序完數組 System.out.println(Arrays.toString(nums)); } /** * 冒泡排序 */ private static void bubbleSort(int[] nums) { for (int i = 1; i < nums.length; i++) { // 判斷標識 boolean flag = true; for (int j = 0; j < nums.length - i; j++) { if (nums[j] > nums[j + 1]) { // 前面數字大于后面的數字，執行位置交換 int temp = nums[j]; nums[j] = nums[j + 1]; nums[j + 1] = temp; // 執行了位置交換，更改標識 flag = false; } } if (flag) { // 沒有可以移動的元素了，跳出循環 break; } } } } ``` 以上程序的執行結果為： ``` [11, 12, 22, 27, 33, 39, 45] ``` 此結果說明，冒泡排序的執行符合我們的預期，執行成功。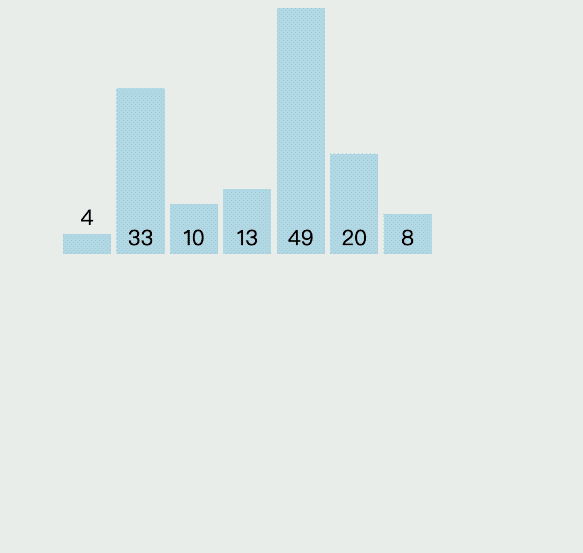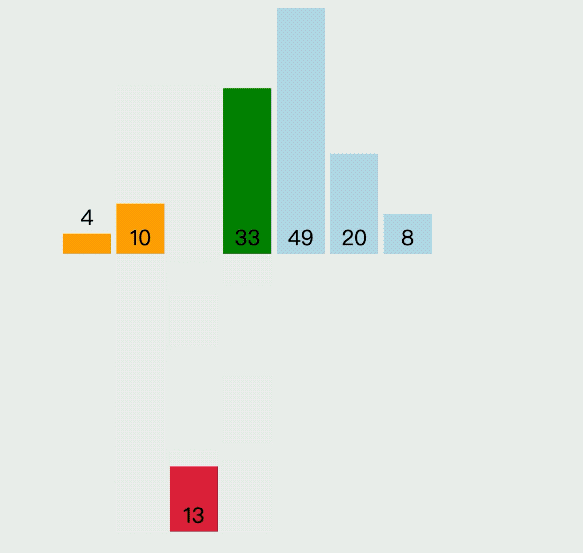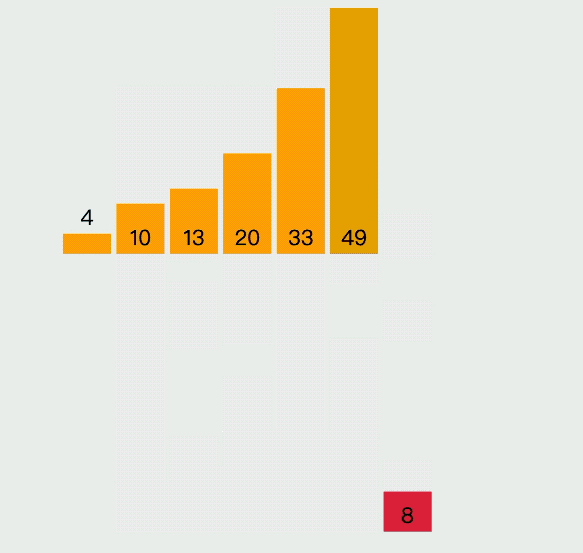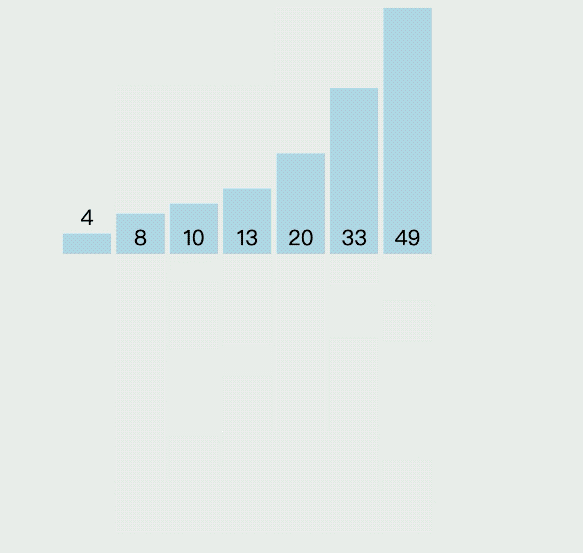 * [ ] 插入排序 插入排序（Insertion Sort）算法是指依次循環當前的列表，通過對比將每個元素插入到合適的位置，它的具體執行過程，如下圖所示：  插入算法的具體實現代碼如下： ``` public class AlgorithmExample { public static void main(String[] args) { int[] insertNums = {4, 33, 10, 13, 49, 20, 8}; // 插入排序調用 insertSort(insertNums); System.out.println("插入排序后：" + Arrays.toString(insertNums)); } /** * 插入排序 */ private static void insertSort(int[] nums) { int i, j, k; for (i = 1; i < nums.length; i++) { k = nums[i]; j = i - 1; // 對 i 之前的數據，給當前元素找到合適的位置 while (j >= 0 && k < nums[j]) { nums[j + 1] = nums[j]; // j-- 繼續往前尋找 j--; } nums[j + 1] = k; } } } ``` 以上程序的執行結果為： ``` 插入排序后：[4, 8, 10, 13, 20, 33, 49] ``` * [ ] 選擇排序 選擇排序（Selection Sort）算法是指依次循環數組，每輪找出最小的值放到數組的最前面，直到循環結束就能得到一個有序數組，它的執行過程如下圖所示：  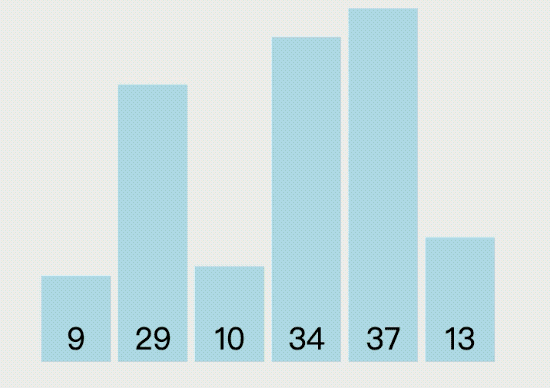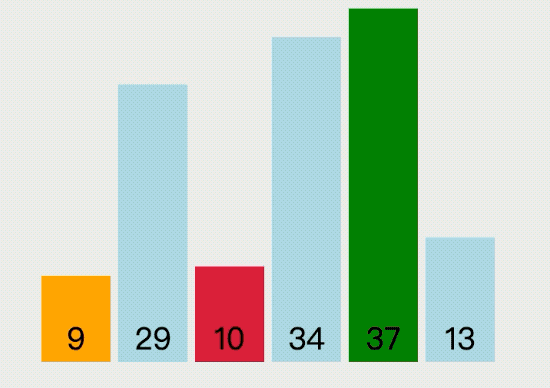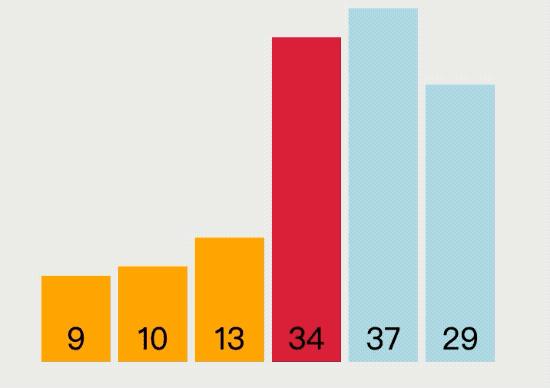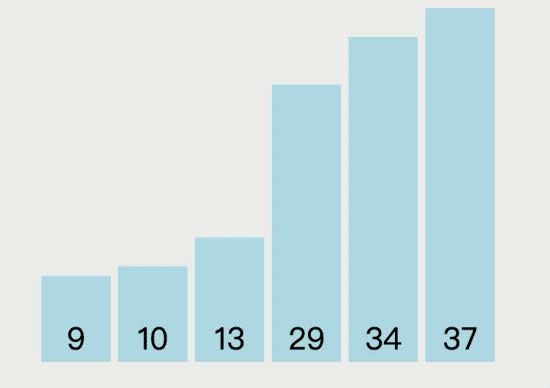選擇排序的具體實現代碼如下： ``` public class AlgorithmExample { public static void main(String[] args) { int[] insertNums = {4, 33, 10, 13, 49, 20, 8}; // 調用選擇排序 selectSort(insertNums); System.out.println("選擇排序后結果：" + Arrays.toString(insertNums)); } /** * 選擇排序 */ private static void selectSort(int[] nums) { int index; int temp; for (int i = 0; i < nums.length - 1; i++) { index = i; for (int j = i + 1; j < nums.length; j++) { if (nums[j] < nums[index]) { index = j; } } if (index != i) { temp = nums[i]; nums[i] = nums[index]; nums[index] = temp; } System.out.print("第" + i + "次排序："); System.out.println(Arrays.toString(nums)); } } } ``` 以上程序的執行結果為： ``` 第0次排序：[4, 33, 10, 13, 49, 20, 8] 第1次排序：[4, 8, 10, 13, 49, 20, 33] 第2次排序：[4, 8, 10, 13, 49, 20, 33] 第3次排序：[4, 8, 10, 13, 49, 20, 33] 第4次排序：[4, 8, 10, 13, 20, 49, 33] 第5次排序：[4, 8, 10, 13, 20, 33, 49] 選擇排序后結果：[4, 8, 10, 13, 20, 33, 49] ``` #### 小結 本著將一個知識點吃透的原則，本課時我們總共介紹了四種算法：冒泡排序算法、二分法、插入排序算法、選擇排序算法等，并且還講了冒泡排序算法的優化。但由于篇幅的原因，這些只能介紹一些常用的算法，如果想要更加深入地學習算法，還需要你投入更多的時間來學習，推薦閱讀《算法》（第 4 版）的內容。