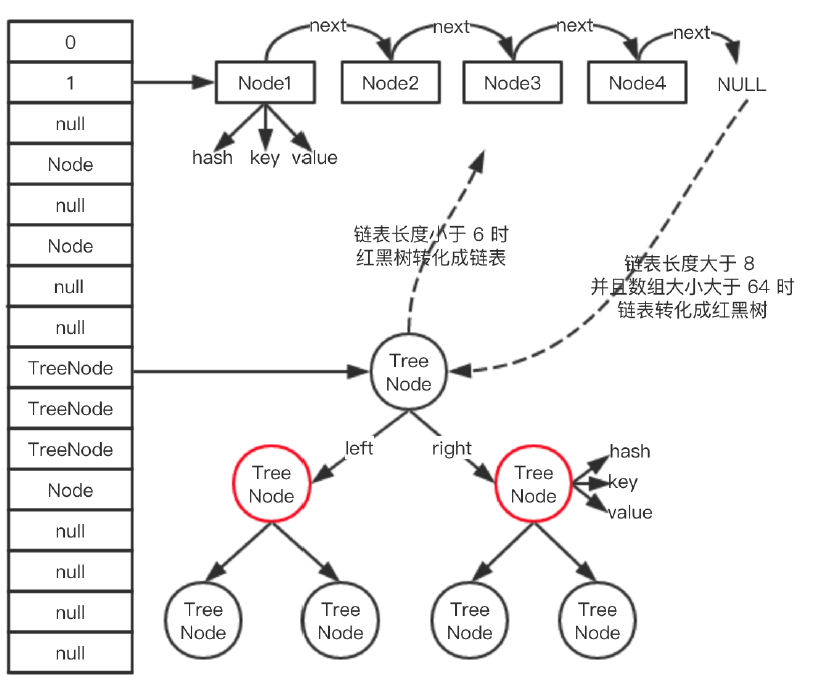
## 08 HashMap 源碼解析 ## 引導語 HashMap 源碼很長，面試的問題也非常多，但這些面試問題，基本都是從源碼中衍生出來的，所以我們只需要弄清楚其底層實現原理，回答這些問題就會游刃有余。 ### 1 整體架構 HashMap 底層的數據結構主要是：數組 + 鏈表 + 紅黑樹。其中當鏈表的長度大于等于 8 時，鏈表會轉化成紅黑樹，當紅黑樹的大小小于等于 6 時，紅黑樹會轉化成鏈表，整體的數據結構如下：  圖中左邊豎著的是 HashMap 的數組結構，數組的元素可能是單個 Node，也可能是個鏈表，也可能是個紅黑樹，比如數組下標索引為 2 的位置就是一個鏈表，下標索引為 9 的位置對應的就是紅黑樹，具體細節我們下文再說。 #### 1.1 類注釋 從 HashMap 的類注釋中，我們可以得到如下信息： ? 允許 null 值，不同于 HashTable ，是線程不安全的； ? load factor （影響因子） 默認值是 0.75， 是均衡了時間和空間損耗算出來的值，較高的值會減少空間開銷（擴容減少，數組大小增長速度變慢），但增加了查找成本（hash 沖突增加，鏈表長度變長），不擴容的條件：數組容量 > 需要的數組大小 /load factor； ? 如果有很多數據需要儲存到 HashMap 中，建議 HashMap 的容量一開始就設置成足夠的大小，這樣可以防止在其過程中不斷的擴容，影響性能； ? HashMap 是非線程安全的，我們可以自己在外部加鎖，或者通過 Collections#synchronizedMap 來實現線程安全，Collections#synchronizedMap 的實現是在每個方法上加上了 synchronized 鎖； ? 在迭代過程中，如果 HashMap 的結構被修改，會快速失敗。 #### 1.2 常見屬性 ``` //初始容量為 16 static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; //最大容量 static final int MAXIMUM_CAPACITY = 1 << 30; //負載因子默認值 static final float DEFAULT_LOAD_FACTOR = 0.75f; //桶上的鏈表長度大于等于8時，鏈表轉化成紅黑樹 static final int TREEIFY_THRESHOLD = 8; //桶上的紅黑樹大小小于等于6時，紅黑樹轉化成鏈表 static final int UNTREEIFY_THRESHOLD = 6; //當數組容量大于 64 時，鏈表才會轉化成紅黑樹 static final int MIN_TREEIFY_CAPACITY = 64; //記錄迭代過程中 HashMap 結構是否發生變化，如果有變化，迭代時會 fail-fast transient int modCount; //HashMap 的實際大小，可能不準(因為當你拿到這個值的時候，可能又發生了變化) transient int size; //存放數據的數組 transient Node<K,V>[] table; // 擴容的門檻，有兩種情況 // 如果初始化時，給定數組大小的話，通過 tableSizeFor 方法計算，數組大小永遠接近于 2 的冪次方，比如你給定初始化大小 19，實際上初始化大小為 32，為 2 的 5 次方。 // 如果是通過 resize 方法進行擴容，大小 = 數組容量 * 0.75 int threshold; //鏈表的節點 static class Node<K,V> implements Map.Entry<K,V> { //紅黑樹的節點 static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> { ``` ### 2 新增 新增 key，value 大概的步驟如下： 1. 空數組有無初始化，沒有的話初始化； 2. 如果通過 key 的 hash 能夠直接找到值，跳轉到 6，否則到 3； 3. 如果 hash 沖突，兩種解決方案：鏈表 or 紅黑樹； 4. 如果是鏈表，遞歸循環，把新元素追加到隊尾； 5. 如果是紅黑樹，調用紅黑樹新增的方法； 6. 通過 2、4、5 將新元素追加成功，再根據 onlyIfAbsent 判斷是否需要覆蓋； 7. 判斷是否需要擴容，需要擴容進行擴容，結束。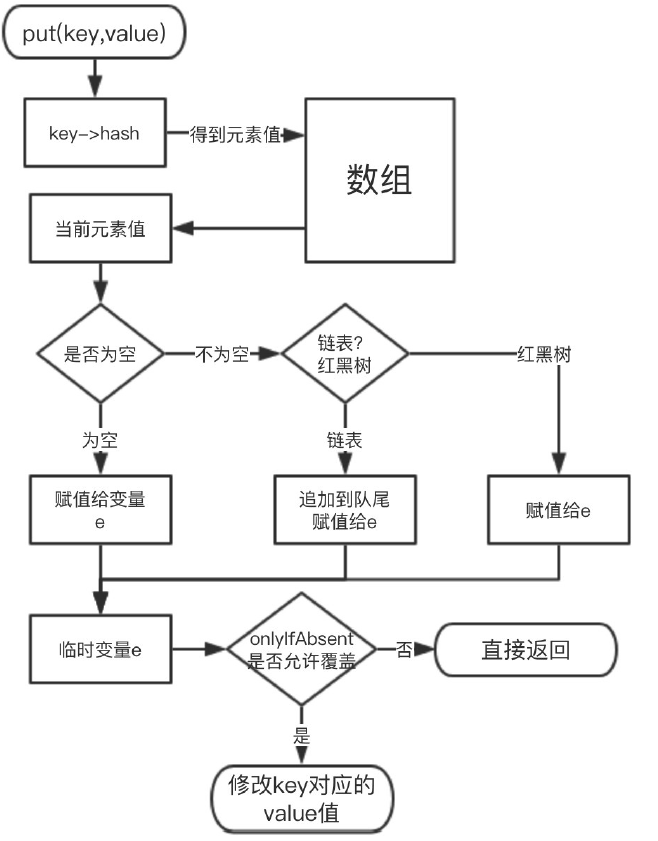 我們來畫一張示意圖來描述下：  代碼細節如下： ``` // 入參 hash：通過 hash 算法計算出來的值。 // 入參 onlyIfAbsent：false 表示即使 key 已經存在了，仍然會用新值覆蓋原來的值，默認為 false final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) { // n 表示數組的長度，i 為數組索引下標，p 為 i 下標位置的 Node 值 Node<K,V>[] tab; Node<K,V> p; int n, i; //如果數組為空，使用 resize 方法初始化 if ((tab = table) == null || (n = tab.length) == 0) n = (tab = resize()).length; // 如果當前索引位置是空的，直接生成新的節點在當前索引位置上 if ((p = tab[i = (n - 1) & hash]) == null) tab[i] = newNode(hash, key, value, null); // 如果當前索引位置有值的處理方法，即我們常說的如何解決 hash 沖突 else { // e 當前節點的臨時變量 Node<K,V> e; K k; // 如果 key 的 hash 和值都相等，直接把當前下標位置的 Node 值賦值給臨時變量 if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k)))) e = p; // 如果是紅黑樹，使用紅黑樹的方式新增 else if (p instanceof TreeNode) e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value); // 是個鏈表，把新節點放到鏈表的尾端 else { // 自旋 for (int binCount = 0; ; ++binCount) { // e = p.next 表示從頭開始，遍歷鏈表 // p.next == null 表明 p 是鏈表的尾節點 if ((e = p.next) == null) { // 把新節點放到鏈表的尾部 p.next = newNode(hash, key, value, null); // 當鏈表的長度大于等于 8 時，鏈表轉紅黑樹 if (binCount >= TREEIFY_THRESHOLD - 1) treeifyBin(tab, hash); break; } // 鏈表遍歷過程中，發現有元素和新增的元素相等，結束循環 if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) break; //更改循環的當前元素，使 p 在遍歷過程中，一直往后移動。 p = e; } } // 說明新節點的新增位置已經找到了 if (e != null) { V oldValue = e.value; // 當 onlyIfAbsent 為 false 時，才會覆蓋值 if (!onlyIfAbsent || oldValue == null) e.value = value; afterNodeAccess(e); // 返回老值 return oldValue; } } // 記錄 HashMap 的數據結構發生了變化 ++modCount; //如果 HashMap 的實際大小大于擴容的門檻，開始擴容 if (++size > threshold) resize(); afterNodeInsertion(evict); return null; } ``` 新增的流程上面應該已經表示很清楚了，接下來我們來看看鏈表和紅黑樹新增的細節： #### 2.1 鏈表的新增 鏈表的新增比較簡單，就是把當前節點追加到鏈表的尾部，和 LinkedList 的追加實現一樣的。 當鏈表長度大于等于 8 時，此時的鏈表就會轉化成紅黑樹，轉化的方法是：treeifyBin，此方法有一個判斷，當鏈表長度大于等于 8，并且整個數組大小大于 64 時，才會轉成紅黑樹，當數組大小小于 64 時，只會觸發擴容，不會轉化成紅黑樹，轉化成紅黑樹的過程也比較簡單，具體轉化的過程源碼可以去 github：https://github.com/luanqiu/java8 上面去查看。 可能面試的時候，有人問你為什么是 8，這個答案在源碼中注釋有說，中文翻譯過來大概的意思是： 鏈表查詢的時間復雜度是 O (n)，紅黑樹的查詢復雜度是 O (log (n))。在鏈表數據不多的時候，使用鏈表進行遍歷也比較快，只有當鏈表數據比較多的時候，才會轉化成紅黑樹，但紅黑樹需要的占用空間是鏈表的 2 倍，考慮到轉化時間和空間損耗，所以我們需要定義出轉化的邊界值。 在考慮設計 8 這個值的時候，我們參考了泊松分布概率函數，由泊松分布中得出結論，鏈表各個長度的命中概率為： ``` * 0: 0.60653066 * 1: 0.30326533 * 2: 0.07581633 * 3: 0.01263606 * 4: 0.00157952 * 5: 0.00015795 * 6: 0.00001316 * 7: 0.00000094 * 8: 0.00000006 ``` 意思是，當鏈表的長度是 8 的時候，出現的概率是 0.00000006，不到千萬分之一，所以說正常情況下，鏈表的長度不可能到達 8 ，而一旦到達 8 時，肯定是 hash 算法出了問題，所以在這種 情況下，為了讓 HashMap 仍然有較高的查詢性能，所以讓鏈表轉化成紅黑樹，我們正常寫代碼，使用 HashMap 時，幾乎不會碰到鏈表轉化成紅黑樹的情況，畢竟概念只有千萬分之一。 #### 2.2 紅黑樹新增節點過程 1. 首先判斷新增的節點在紅黑樹上是不是已經存在，判斷手段有如下兩種： 1.1. 如果節點沒有實現 Comparable 接口，使用 equals 進行判斷； 1.2. 如果節點自己實現了 Comparable 接口，使用 compareTo 進行判斷。 2. 新增的節點如果已經在紅黑樹上，直接返回；不在的話，判斷新增節點是在當前節點的左邊還是右邊，左邊值小，右邊值大； 3. 自旋遞歸 1 和 2 步，直到當前節點的左邊或者右邊的節點為空時，停止自旋，當前節點即為我們新增節點的父節點； 4. 把新增節點放到當前節點的左邊或右邊為空的地方，并于當前節點建立父子節點關系； 5. 進行著色和旋轉，結束。 具體源碼如下： ``` //入參 h：key 的hash值 final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab, int h, K k, V v) { Class<?> kc = null; boolean searched = false; //找到根節點 TreeNode<K,V> root = (parent != null) ? root() : this; //自旋 for (TreeNode<K,V> p = root;;) { int dir, ph; K pk; // p hash 值大于 h，說明 p 在 h 的右邊 if ((ph = p.hash) > h) dir = -1; // p hash 值小于 h，說明 p 在 h 的左邊 else if (ph < h) dir = 1; //要放進去key在當前樹中已經存在了(equals來判斷) else if ((pk = p.key) == k || (k != null && k.equals(pk))) return p; //自己實現的Comparable的話，不能用hashcode比較了，需要用compareTo else if ((kc == null && //得到key的Class類型，如果key沒有實現Comparable就是null (kc = comparableClassFor(k)) == null) || //當前節點pk和入參k不等 (dir = compareComparables(kc, k, pk)) == 0) { if (!searched) { TreeNode<K,V> q, ch; searched = true; if (((ch = p.left) != null && (q = ch.find(h, k, kc)) != null) || ((ch = p.right) != null && (q = ch.find(h, k, kc)) != null)) return q; } dir = tieBreakOrder(k, pk); } TreeNode<K,V> xp = p; //找到和當前hashcode值相近的節點(當前節點的左右子節點其中一個為空即可) if ((p = (dir <= 0) ? p.left : p.right) == null) { Node<K,V> xpn = xp.next; //生成新的節點 TreeNode<K,V> x = map.newTreeNode(h, k, v, xpn); //把新節點放在當前子節點為空的位置上 if (dir <= 0) xp.left = x; else xp.right = x; //當前節點和新節點建立父子，前后關系 xp.next = x; x.parent = x.prev = xp; if (xpn != null) ((TreeNode<K,V>)xpn).prev = x; //balanceInsertion 對紅黑樹進行著色或旋轉，以達到更多的查找效率，著色或旋轉的幾種場景如下 //著色：新節點總是為紅色；如果新節點的父親是黑色，則不需要重新著色；如果父親是紅色，那么必須通過重新著色或者旋轉的方法，再次達到紅黑樹的5個約束條件 //旋轉： 父親是紅色，叔叔是黑色時，進行旋轉 //如果當前節點是父親的右節點，則進行左旋 //如果當前節點是父親的左節點，則進行右旋 //moveRootToFront 方法是把算出來的root放到根節點上 moveRootToFront(tab, balanceInsertion(root, x)); return null; } } } ``` 紅黑樹的新增，要求大家對紅黑樹的數據結構有一定的了解。面試的時候，一般只會問到新增節點到紅黑樹上大概是什么樣的一個過程，著色和旋轉的細節不會問，因為很難說清楚，但我們要清楚著色指的是給紅黑樹的節點著上紅色或黑色，旋轉是為了讓紅黑樹更加平衡，提高查詢的效率，總的來說都是為了滿足紅黑樹的 5 個原則： 1. 節點是紅色或黑色 2. 根是黑色 3. 所有葉子都是黑色 4. 從任一節點到其每個葉子的所有簡單路徑都包含相同數目的黑色節點 5. 從每個葉子到根的所有路徑上不能有兩個連續的紅色節點 ### 3 查找 HashMap 的查找主要分為以下三步： ? 根據 hash 算法定位數組的索引位置，equals 判斷當前節點是否是我們需要尋找的 key，是的話直接返回，不是的話往下。 ? 判斷當前節點有無 next 節點，有的話判斷是鏈表類型，還是紅黑樹類型。 ? 分別走鏈表和紅黑樹不同類型的查找方法。 鏈表查找的關鍵代碼是： ``` // 采用自旋方式從鏈表中查找 key，e 初始為為鏈表的頭節點 do { // 如果當前節點 hash 等于 key 的 hash，并且 equals 相等，當前節點就是我們要找的節點 // 當 hash 沖突時，同一個 hash 值上是一個鏈表的時候，我們是通過 equals 方法來比較 key 是否相等的 if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) return e; // 否則，把當前節點的下一個節點拿出來繼續尋找 } while ((e = e.next) != null); ``` 紅黑樹查找的代碼很多，我們大概說下思路，實際步驟比較復雜，可以去 github 上面去查看源碼： 1. 從根節點遞歸查找； 2. 根據 hashcode，比較查找節點，左邊節點，右邊節點之間的大小，根本紅黑樹左小右大的特性進行判斷； 3. 判斷查找節點在第 2 步有無定位節點位置，有的話返回，沒有的話重復 2，3 兩步； 4. 一直自旋到定位到節點位置為止。 如果紅黑樹比較平衡的話，每次查找的次數就是樹的深度。 ### 總結 HashMap 的內容雖然較多，但大多數 api 都只是對數組 + 鏈表 + 紅黑樹這種數據結構進行封裝而已，本小節我們從新增和查找兩個角度進行了源碼的深入分析，分析了是如何對數組、鏈表和紅黑樹進行操作的。想了解更多，可以前往 github 上查看更多源碼。