# 二、一個完整的機器學習項目 > 譯者：[@SeanCheney](https://www.jianshu.com/u/130f76596b02) > > 校對者：[@Lisanaaa](https://github.com/Lisanaaa)、[@飛龍](https://github.com/wizardforcel)、[@PeterHo](https://github.com/PeterHo)、[@ZhengqiJiang](https://github.com/AnEscapist)、[@tabeworks](https://github.com/tabeworks) 本章中，你會假裝作為被一家地產公司剛剛雇傭的數據科學家，完整地學習一個案例項目。下面是主要步驟： 1. 項目概述。 2. 獲取數據。 3. 發現并可視化數據，發現規律。 4. 為機器學習算法準備數據。 5. 選擇模型，進行訓練。 6. 微調模型。 7. 給出解決方案。 8. 部署、監控、維護系統。 ## 使用真實數據 學習機器學習時，最好使用真實數據，而不是人工數據集。幸運的是，有上千個開源數據集可以進行選擇，涵蓋多個領域。以下是一些可以查找的數據的地方： * 流行的開源數據倉庫： + [UC Irvine Machine Learning Repository](https://link.jianshu.com?t=http%3A%2F%2Farchive.ics.uci.edu%2Fml%2F) + [Kaggle datasets](https://link.jianshu.com?t=https%3A%2F%2Fwww.kaggle.com%2Fdatasets) + [Amazon’s AWS datasets](https://link.jianshu.com?t=http%3A%2F%2Faws.amazon.com%2Ffr%2Fdatasets%2F) * 準入口（提供開源數據列表） + [http://dataportals.org/](https://link.jianshu.com?t=http%3A%2F%2Fdataportals.org%2F) + [http://opendatamonitor.eu/](https://link.jianshu.com?t=http%3A%2F%2Fopendatamonitor.eu%2F) + [http://quandl.com/](https://link.jianshu.com?t=http%3A%2F%2Fquandl.com%2F) * 其它列出流行開源數據倉庫的網頁： + [Wikipedia’s list of Machine Learning datasets](https://link.jianshu.com?t=https%3A%2F%2Fgoo.gl%2FSJHN2k) + [Quora.com question](https://link.jianshu.com?t=http%3A%2F%2Fgoo.gl%2FzDR78y) + [Datasets subreddit](https://link.jianshu.com?t=https%3A%2F%2Fwww.reddit.com%2Fr%2Fdatasets) 本章，我們選擇的是 StatLib 的加州房產價格數據集（見圖 2-1）。這個數據集是基于 1990 年加州普查的數據。數據已經有點老（1990 年還能買一個灣區不錯的房子），但是它有許多優點，利于學習，所以假設這個數據為最近的。為了便于教學，我們添加了一個類別屬性，并除去了一些。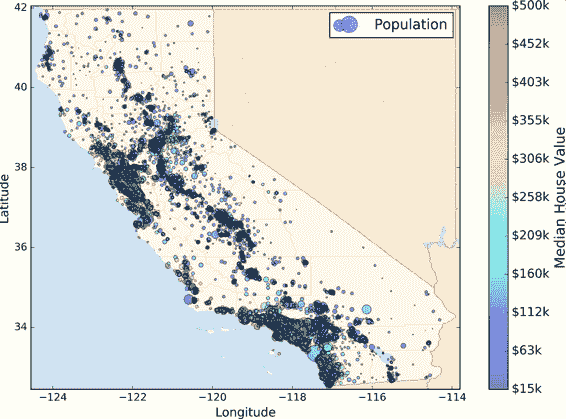  圖 2-1 加州房產價格 ## 項目概覽 歡迎來到機器學習房地產公司！你的第一個任務是利用加州普查數據，建立一個加州房價模型。這個數據包含每個街區組的人口、收入中位數、房價中位數等指標。 街區組是美國調查局發布樣本數據的最小地理單位（一個街區通常有 600 到 3000 人）。我們將其簡稱為“街區”。 你的模型要利用這個數據進行學習，然后根據其它指標，預測任何街區的的房價中位數。 > 提示：你是一個有條理的數據科學家，你要做的第一件事是拿出你的機器學習項目清單。你可以使用附錄 B 中的清單；這個清單適用于大多數的機器學習項目，但是你還是要確認它是否滿足需求。在本章中，我們會檢查許多清單上的項目，但是也會跳過一些簡單的，有些會在后面的章節再討論。 ### 劃定問題 問老板的第一個問題應該是商業目標是什么？建立模型可能不是最終目標。公司要如何使用、并從模型受益？這非常重要，因為它決定了如何劃定問題，要選擇什么算法，評估模型性能的指標是什么，要花多少精力進行微調。 老板告訴你你的模型的輸出（一個區的房價中位數）會傳給另一個機器學習系統（見圖 2-2），也有其它信號會傳入后面的系統。這一整套系統可以確定某個區進行投資值不值。確定值不值得投資非常重要，它直接影響利潤。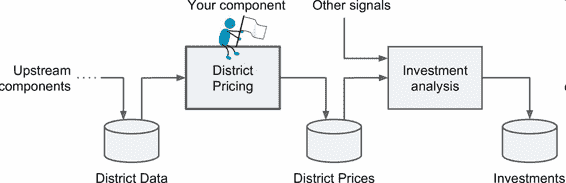  圖 2-2 房地產投資的機器學習流水線 > 流水線 > > 一系列的數據處理組件被稱為數據流水線。流水線在機器學習系統中很常見，因為有許多數據要處理和轉換。 > > 組件通常是異步運行的。每個組件吸納進大量數據，進行處理，然后將數據傳輸到另一個數據容器中，而后流水線中的另一個組件收入這個數據，然后輸出，這個過程依次進行下去。每個組件都是獨立的：組件間的接口只是數據容器。這樣可以讓系統更便于理解（記住數據流的圖），不同的項目組可以關注于不同的組件。進而，如果一個組件失效了，下游的組件使用失效組件最后生產的數據，通常可以正常運行（一段時間）。這樣就使整個架構相當健壯。 > > 另一方面，如果沒有監控，失效的組件會在不被注意的情況下運行一段時間。數據會受到污染，整個系統的性能就會下降。 下一個要問的問題是，現在的解決方案效果如何。老板通常會給一個參考性能，以及如何解決問題。老板說，現在街區的房價是靠專家手工估計的，專家隊伍收集最新的關于一個區的信息（不包括房價中位數），他們使用復雜的規則進行估計。這種方法費錢費時間，而且估計結果不理想，誤差率大概有 15%。 OK，有了這些信息，你就可以開始設計系統了。首先，你需要劃定問題：監督或非監督，還是強化學習？這是個分類任務、回歸任務，還是其它的？要使用批量學習還是線上學習？繼續閱讀之前，請暫停一下，嘗試自己回答下這些問題。 你能回答出來嗎？一起看下答案：很明顯，這是一個典型的監督學習任務，因為你要使用的是有標簽的訓練樣本（每個實例都有預定的產出，即街區的房價中位數）。并且，這是一個典型的回歸任務，因為你要預測一個值。講的更細些，這是一個多變量回歸問題，因為系統要使用多個變量進行預測（要使用街區的人口，收入中位數等等）。在第一章中，你只是根據人均 GDP 來預測生活滿意度，因此這是一個單變量回歸問題。最后，沒有連續的數據流進入系統，沒有特別需求需要對數據變動作出快速適應。數據量不大可以放到內存中，因此批量學習就夠了。 > 提示：如果數據量很大，你可以要么在多個服務器上對批量學習做拆分（使用 MapReduce 技術，后面會看到），或是使用線上學習。 ### 選擇性能指標 下一步是選擇性能指標。回歸問題的典型指標是均方根誤差（RMSE）。均方根誤差測量的是系統預測誤差的標準差。例如，RMSE 等于 50000，意味著，68% 的系統預測值位于實際值的 50000 美元以內，95% 的預測值位于實際值的 100000 美元以內（一個特征通常都符合高斯分布，即滿足 “68-95-99.7”規則：大約 68%的值落在`1σ`內，95% 的值落在`2σ`內，99.7%的值落在`3σ`內，這里的`σ`等于 50000）。公式 2-1 展示了計算 RMSE 的方法。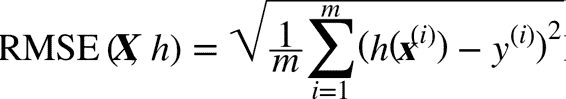  公式 2-1 均方根誤差（RMSE） > 符號的含義 > > 這個方程引入了一些常見的貫穿本書的機器學習符號： > > * `m`是測量 RMSE 的數據集中的實例數量。 > 例如，如果用一個含有 2000 個街區的驗證集求 RMSE，則`m = 2000`。 > > *  是數據集第`i`個實例的所有特征值（不包含標簽）的向量， 是它的標簽（這個實例的輸出值）。? 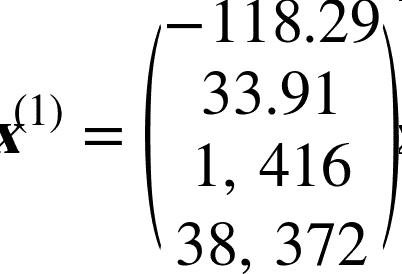> > 例如，如果數據集中的第一個街區位于經度 –118.29°，緯度 33.91°，有 1416 名居民，收入中位數是 38372 美元，房價中位數是 156400 美元（忽略掉其它的特征），則有： > >  > > 和， > >  > > * `X`是包含數據集中所有實例的所有特征值（不包含標簽）的矩陣。每一行是一個實例，第`i`行是  的轉置，記為 。 > > 例如，仍然是前面提到的第一區，矩陣`X`就是： > >  > > * `h`是系統的預測函數，也稱為假設（hypothesis）。當系統收到一個實例的特征向量 ，就會輸出這個實例的一個預測值 （ 讀作`y-hat`）。 > > 例如，如果系統預測第一區的房價中位數是 158400 美元，則 。預測誤差是 。 > > * `RMSE(X,h)`是使用假設`h`在樣本集上測量的損失函數。 > > 我們使用小寫斜體表示標量值（例如  或 ）和函數名（例如 ），小寫粗體表示向量（例如 ），大寫粗體表示矩陣（例如 ）。 雖然大多數時候 RMSE 是回歸任務可靠的性能指標，在有些情況下，你可能需要另外的函數。例如，假設存在許多異常的街區。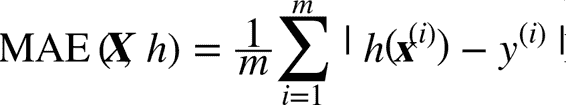此時，你可能需要使用平均絕對誤差（Mean Absolute Error，也稱作平均絕對偏差），見公式 2-2：  公式 2-2 平均絕對誤差 RMSE 和 MAE 都是測量預測值和目標值兩個向量距離的方法。有多種測量距離的方法，或范數： * 計算對應歐幾里得范數的平方和的根（RMSE）：這個距離介紹過。它也稱作`?2`范數，標記為 （或只是 ）。 * 計算對應于`?1`（標記為 ）范數的絕對值和（MAE）。有時，也稱其為曼哈頓范數，因為它測量了城市中的兩點，沿著矩形的邊行走的距離。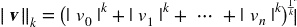 * 更一般的，包含`n`個元素的向量`v`的`?k`范數（K 階閔氏范數），定義成  `?0`（漢明范數）只顯示了這個向量的基數（即，非零元素的個數），`?∞`（切比雪夫范數）是向量中最大的絕對值。 * 范數的指數越高，就越關注大的值而忽略小的值。這就是為什么 RMSE 比 MAE 對異常值更敏感。但是當異常值是指數分布的（類似正態曲線），RMSE 就會表現很好。 ### 核實假設 最后，最好列出并核對迄今（你或其他人）作出的假設，這樣可以盡早發現嚴重的問題。例如，你的系統輸出的街區房價，會傳入到下游的機器學習系統，我們假設這些價格確實會被當做街區房價使用。但是如果下游系統實際上將價格轉化成了分類（例如，便宜、中等、昂貴），然后使用這些分類，而不是使用價格。這樣的話，獲得準確的價格就不那么重要了，你只需要得到合適的分類。問題相應地就變成了一個分類問題，而不是回歸任務。你可不想在一個回歸系統上工作了數月，最后才發現真相。 幸運的是，在與下游系統主管探討之后，你很確信他們需要的就是實際的價格，而不是分類。很好！整裝待發，可以開始寫代碼了。 ## 獲取數據 開始動手。最后用 Jupyter notebook 完整地敲一遍示例代碼。完整的代碼位于 <https://github.com/ageron/handson-ml>。 ### 創建工作空間 首先，你需要安裝 Python。可能已經安裝過了，沒有的話，可以從官網下載 <https://www.python.org/>。 接下來，需要為你的機器學習代碼和數據集創建工作空間目錄。打開一個終端，輸入以下命令（在提示符`$`之后）： <pre><code> &#x24; export ML_PATH="&#x24;HOME/ml" # 可以更改路徑 &#x24; mkdir -p &#x24;ML_PATH </code></pre> 還需要一些 Python 模塊：Jupyter、NumPy、Pandas、Matplotlib 和 Scikit-Learn。如果所有這些模塊都已經在 Jupyter 中運行了，你可以直接跳到下一節“下載數據”。如果還沒安裝，有多種方法可以進行安裝（包括它們的依賴）。你可以使用系統的包管理系統（比如 Ubuntu 上的`apt-get`，或 macOS 上的 MacPorts 或 HomeBrew），安裝一個 Python 科學計算環境比如 Anaconda，使用 Anaconda 的包管理系統，或者使用 Python 自己的包管理器`pip`，它是 Python 安裝包（自從 2.7.9 版本）自帶的。可以用下面的命令檢測是否安裝`pip`： ``` $ pip3 --version pip 9.0.1 from [...]/lib/python3.5/site-packages (python 3.5) ``` 你需要保證`pip`是近期的版本，至少高于 1.4，以保障二進制模塊文件的安裝（也稱為 wheel）。要升級`pip`，可以使用下面的命令： ``` $ pip3 install --upgrade pip Collecting pip [...] Successfully installed pip-9.0.1 ``` > 創建獨立環境 > > 如果你希望在一個獨立環境中工作（強烈推薦這么做，不同項目的庫的版本不會沖突），用下面的`pip`命令安裝`virtualenv`： > > ``` > $ pip3 install --user --upgrade virtualenv > Collecting virtualenv > [...] > Successfully installed virtualenv > > ``` > > 現在可以通過下面命令創建一個獨立的 Python 環境： > > <pre><code> > &#x24; cd &#x24;ML_PATH > &#x24; virtualenv env > Using base prefix '[...]' > New python executable in [...]/ml/env/bin/python3.5 > Also creating executable in [...]/ml/env/bin/python > Installing setuptools, pip, wheel...done. > </code></pre> > > 以后每次想要激活這個環境,只需打開一個終端然后輸入： > > <pre><code> > &#x24; cd &#x24;ML_PATH > &#x24; source env/bin/activate > </code></pre> > > 啟動該環境時，使用`pip`安裝的任何包都只安裝于這個獨立環境中，Python 指揮訪問這些包（如果你希望 Python 能訪問系統的包，創建環境時要使用包選項`--system-site`）。更多信息，請查看`virtualenv`文檔。 現在，你可以使用`pip`命令安裝所有必需的模塊和它們的依賴： ``` $ pip3 install --upgrade jupyter matplotlib numpy pandas scipy scikit-learn Collecting jupyter Downloading jupyter-1.0.0-py2.py3-none-any.whl Collecting matplotlib [...] ``` 要檢查安裝，可以用下面的命令引入每個模塊： ``` $ python3 -c "import jupyter, matplotlib, numpy, pandas, scipy, sklearn" ``` 這個命令不應該有任何輸出和錯誤。現在你可以用下面的命令打開 Jupyter： ``` $ jupyter notebook [I 15:24 NotebookApp] Serving notebooks from local directory: [...]/ml [I 15:24 NotebookApp] 0 active kernels [I 15:24 NotebookApp] The Jupyter Notebook is running at: http://localhost:8888/ [I 15:24 NotebookApp] Use Control-C to stop this server and shut down all kernels (twice to skip confirmation). ``` Jupyter 服務器現在運行在終端上，監聽 888 8 端口。你可以用瀏覽器打開`http://localhost:8888/`，以訪問這個服務器（服務器啟動時，通常就自動打開了）。你可以看到一個空的工作空間目錄（如果按照先前的`virtualenv`步驟，只包含`env`目錄）。 現在點擊按鈕 New 創建一個新的 Python 注本，選擇合適的 Python 版本（見圖 2-3）。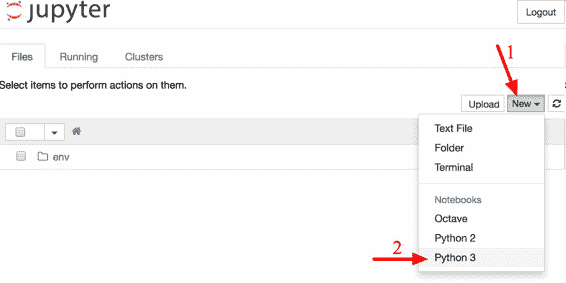  圖 2-3 Jupyter 的工作空間 這一步做了三件事：首先，在工作空間中創建了一個新的 notebook 文件`Untitled.ipynb`；第二，它啟動了一個 Jupyter 的 Python 內核來運行這個 notebook；第三，在一個新欄中打開這個 notebook。接下來，點擊 Untitled，將這個 notebook 重命名為`Housing`（這會將`ipynb`文件自動命名為`Housing.ipynb`）。 notebook 包含一組代碼框。每個代碼框可以放入可執行代碼或格式化文本。現在，notebook 只有一個空的代碼框，標簽是`In [1]:`。在框中輸入`print("Hello world!")`，點擊運行按鈕（見圖 2-4）或按`Shift+Enter`。這會將當前的代碼框發送到 Python 內核，運行之后會返回輸出。結果顯示在代碼框下方。由于抵達了 notebook 的底部，一個新的代碼框會被自動創建出來。從 Jupyter 的 Help 菜單中的 User Interface Tour，可以學習 Jupyter 的基本操作。  圖 2-4 在 notebook 中打印`Hello world!` ### 下載數據 一般情況下，數據是存儲于關系型數據庫（或其它常見數據庫）中的多個表、文檔、文件。要訪問數據，你首先要有密碼和登錄權限，并要了解數據模式。但是在這個項目中，這一切要簡單些：只要下載一個壓縮文件，`housing.tgz`，它包含一個 CSV 文件`housing.csv`，含有所有數據。 你可以使用瀏覽器下載，運行`tar xzf housing.tgz`解壓出`csv`文件，但是更好的辦法是寫一個小函數來做這件事。如果數據變動頻繁，這么做是非常好的，因為可以讓你寫一個小腳本隨時獲取最新的數據（或者創建一個定時任務來做）。如果你想在多臺機器上安裝數據集，獲取數據自動化也是非常好的。 下面是獲取數據的函數： ```python import os import tarfile from six.moves import urllib DOWNLOAD_ROOT = "https://raw.githubusercontent.com/ageron/handson-ml/master/" HOUSING_PATH = "datasets/housing" HOUSING_URL = DOWNLOAD_ROOT + HOUSING_PATH + "/housing.tgz" def fetch_housing_data(housing_url=HOUSING_URL, housing_path=HOUSING_PATH): if not os.path.isdir(housing_path): os.makedirs(housing_path) tgz_path = os.path.join(housing_path, "housing.tgz") urllib.request.urlretrieve(housing_url, tgz_path) housing_tgz = tarfile.open(tgz_path) housing_tgz.extractall(path=housing_path) housing_tgz.close() ``` 現在，當你調用`fetch_housing_data()`，就會在工作空間創建一個`datasets/housing`目錄，下載`housing.tgz`文件，解壓出`housing.csv`。 然后使用 Pandas 加載數據。還是用一個小函數來加載數據： ```python import pandas as pd def load_housing_data(housing_path=HOUSING_PATH): csv_path = os.path.join(housing_path, "housing.csv") return pd.read_csv(csv_path) ``` 這個函數會返回一個包含所有數據的 Pandas `DataFrame` 對象。 ### 快速查看數據結構 使用`DataFrame`的`head()`方法查看該數據集的前 5 行（見圖 2-5）。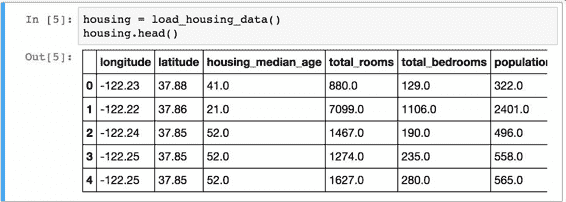  圖 2-5 數據集的前五行 每一行都表示一個街區。共有 10 個屬性（截圖中可以看到 6 個）：經度、維度、房屋年齡中位數、總房間數、總臥室數、人口數、家庭數、收入中位數、房屋價值中位數、離大海距離。 `info()`方法可以快速查看數據的描述，特別是總行數、每個屬性的類型和非空值的數量（見圖 2-6）。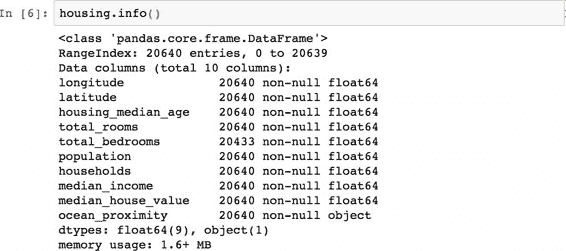  圖 2-6 房屋信息 數據集中共有 20640 個實例，按照機器學習的標準這個數據量很小，但是非常適合入門。我們注意到總臥室數只有 20433 個非空值，這意味著有 207 個街區缺少這個值。我們將在后面對它進行處理。 所有的屬性都是數值的，除了離大海距離這項。它的類型是對象，因此可以包含任意 Python 對象，但是因為該項是從 CSV 文件加載的，所以必然是文本類型。在剛才查看數據前五項時，你可能注意到那一列的值是重復的，意味著它可能是一項表示類別的屬性。可以使用`value_counts()`方法查看該項中都有哪些類別，每個類別中都包含有多少個街區： ```python >>> housing["ocean_proximity"].value_counts() <1H OCEAN 9136 INLAND 6551 NEAR OCEAN 2658 NEAR BAY 2290 ISLAND 5 Name: ocean_proximity, dtype: int64 ``` 再來看其它字段。`describe()`方法展示了數值屬性的概括（見圖 2-7）。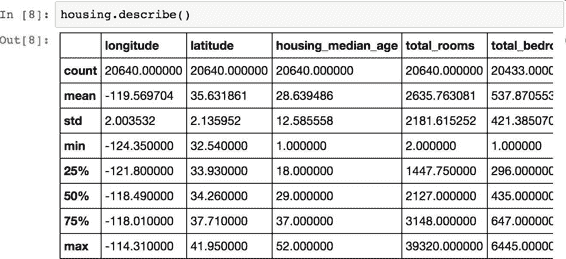  圖 2-7 每個數值屬性的概括 `count`、`mean`、`min`和`max`幾行的意思很明顯了。注意，空值被忽略了（所以，臥室總數是 20433 而不是 20640）。`std`是標準差（揭示數值的分散度）。25%、50%、75% 展示了對應的分位數：每個分位數指明小于這個值，且指定分組的百分比。例如，25% 的街區的房屋年齡中位數小于 18，而 50% 的小于 29，75% 的小于 37。這些值通常稱為第 25 個百分位數（或第一個四分位數），中位數，第 75 個百分位數（第三個四分位數）。 另一種快速了解數據類型的方法是畫出每個數值屬性的柱狀圖。柱狀圖（的縱軸）展示了特定范圍的實例的個數。你還可以一次給一個屬性畫圖，或對完整數據集調用`hist()`方法，后者會畫出每個數值屬性的柱狀圖（見圖 2-8）。例如，你可以看到略微超過 800 個街區的`median_house_value`值差不多等于 500000 美元。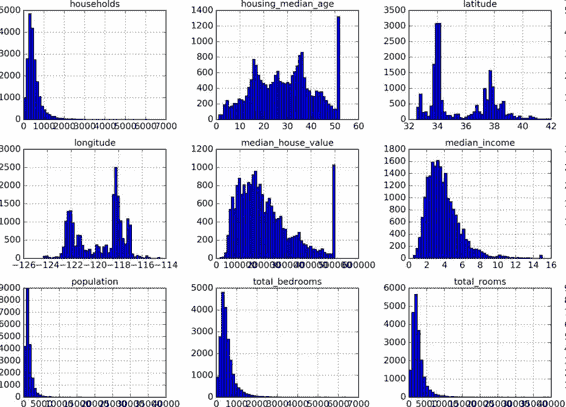 ```python %matplotlib inline # only in a Jupyter notebook import matplotlib.pyplot as plt housing.hist(bins=50, figsize=(20,15)) plt.show() ```  圖 2-8 每個數值屬性的柱狀圖 > 注：`hist()`方法依賴于 Matplotlib，后者依賴于用戶指定的圖形后端以打印到屏幕上。因此在畫圖之前，你要指定 Matplotlib 要使用的后端。最簡單的方法是使用 Jupyter 的魔術命令`%matplotlib inline`。它會告訴 Jupyter 設定好 Matplotlib，以使用 Jupyter 自己的后端。繪圖就會在 notebook 中渲染了。注意在 Jupyter 中調用`show()`不是必要的，因為代碼框執行后 Jupyter 會自動展示圖像。 注意柱狀圖中的一些點： 1. 首先，收入中位數貌似不是美元（USD）。與數據采集團隊交流之后，你被告知數據是經過縮放調整的，過高收入中位數的會變為 15（實際為 15.0001），過低的會變為 5（實際為 0.4999）。在機器學習中對數據進行預處理很正常，這不一定是個問題，但你要明白數據是如何計算出來的。 2. 房屋年齡中位數和房屋價值中位數也被設了上限。后者可能是個嚴重的問題，因為它是你的目標屬性（你的標簽）。你的機器學習算法可能學習到價格不會超出這個界限。你需要與下游團隊核實，這是否會成為問題。如果他們告訴你他們需要明確的預測值，即使超過 500000 美元，你則有兩個選項： 1. 對于設了上限的標簽，重新收集合適的標簽； 2. 將這些街區從訓練集移除（也從測試集移除，因為若房價超出 500000 美元，你的系統就會被差評）。 3. 這些屬性值有不同的量度。我們會在本章后面討論特征縮放。 4. 最后，許多柱狀圖的尾巴很長：相較于左邊，它們在中位數的右邊延伸過遠。對于某些機器學習算法，這會使檢測規律變得更難些。我們會在后面嘗試變換處理這些屬性，使其變為正態分布。 希望你現在對要處理的數據有一定了解了。 > 警告：稍等！在你進一步查看數據之前，你需要創建一個測試集，將它放在一旁，千萬不要再看它。 ### 創建測試集 在這個階段就分割數據，聽起來很奇怪。畢竟，你只是簡單快速地查看了數據而已，你需要再仔細調查下數據以決定使用什么算法。這么想是對的，但是人類的大腦是一個神奇的發現規律的系統，這意味著大腦非常容易發生過擬合：如果你查看了測試集，就會不經意地按照測試集中的規律來選擇某個特定的機器學習模型。再當你使用測試集來評估誤差率時，就會導致評估過于樂觀，而實際部署的系統表現就會差。這稱為數據透視偏差。 理論上，創建測試集很簡單：只要隨機挑選一些實例，一般是數據集的 20%，放到一邊： ```python import numpy as np def split_train_test(data, test_ratio): shuffled_indices = np.random.permutation(len(data)) test_set_size = int(len(data) * test_ratio) test_indices = shuffled_indices[:test_set_size] train_indices = shuffled_indices[test_set_size:] return data.iloc[train_indices], data.iloc[test_indices] ``` 然后可以像下面這樣使用這個函數： ```python >>> train_set, test_set = split_train_test(housing, 0.2) >>> print(len(train_set), "train +", len(test_set), "test") 16512 train + 4128 test ``` 這個方法可行，但是并不完美：如果再次運行程序，就會產生一個不同的測試集！多次運行之后，你（或你的機器學習算法）就會得到整個數據集，這是需要避免的。 解決的辦法之一是保存第一次運行得到的測試集，并在隨后的過程加載。另一種方法是在調用`np.random.permutation()`之前，設置隨機數生成器的種子（比如`np.random.seed(42)`），以產生總是相同的洗牌指數（shuffled indices）。 但是如果數據集更新，這兩個方法都會失效。一個通常的解決辦法是使用每個實例的 ID 來判定這個實例是否應該放入測試集（假設每個實例都有唯一并且不變的 ID）。例如，你可以計算出每個實例 ID 的哈希值，只保留其最后一個字節，如果該值小于等于 51（約為 256 的 20%），就將其放入測試集。這樣可以保證在多次運行中，測試集保持不變，即使更新了數據集。新的測試集會包含新實例中的 20%，但不會有之前位于訓練集的實例。下面是一種可用的方法： ```python import hashlib def test_set_check(identifier, test_ratio, hash): return hash(np.int64(identifier)).digest()[-1] < 256 * test_ratio def split_train_test_by_id(data, test_ratio, id_column, hash=hashlib.md5): ids = data[id_column] in_test_set = ids.apply(lambda id_: test_set_check(id_, test_ratio, hash)) return data.loc[~in_test_set], data.loc[in_test_set] ``` 不過，房產數據集沒有 ID 這一列。最簡單的方法是使用行索引作為 ID： ```python housing_with_id = housing.reset_index() # adds an `index` column train_set, test_set = split_train_test_by_id(housing_with_id, 0.2, "index") ``` 如果使用行索引作為唯一識別碼，你需要保證新數據都放到現有數據的尾部，且沒有行被刪除。如果做不到，則可以用最穩定的特征來創建唯一識別碼。例如，一個區的維度和經度在幾百萬年之內是不變的，所以可以將兩者結合成一個 ID： ```python housing_with_id["id"] = housing["longitude"] * 1000 + housing["latitude"] train_set, test_set = split_train_test_by_id(housing_with_id, 0.2, "id") ``` Scikit-Learn 提供了一些函數，可以用多種方式將數據集分割成多個子集。最簡單的函數是`train_test_split`，它的作用和之前的函數`split_train_test`很像，并帶有其它一些功能。首先，它有一個`random_state`參數，可以設定前面講過的隨機生成器種子；第二，你可以將種子傳遞給多個行數相同的數據集，可以在相同的索引上分割數據集（這個功能非常有用，比如你的標簽值是放在另一個`DataFrame`里的）： ```python from sklearn.model_selection import train_test_split train_set, test_set = train_test_split(housing, test_size=0.2, random_state=42) ``` 目前為止，我們采用的都是純隨機的取樣方法。當你的數據集很大時（尤其是和屬性數相比），這通常可行；但如果數據集不大，就會有采樣偏差的風險。當一個調查公司想要對 1000 個人進行調查，它們不是在電話亭里隨機選 1000 個人出來。調查公司要保證這 1000 個人對人群整體有代表性。例如，美國人口的 51.3% 是女性，48.7% 是男性。所以在美國，嚴謹的調查需要保證樣本也是這個比例：513 名女性，487 名男性。這稱作分層采樣（stratified sampling）：將人群分成均勻的子分組，稱為分層，從每個分層去取合適數量的實例，以保證測試集對總人數有代表性。如果調查公司采用純隨機采樣，會有 12% 的概率導致采樣偏差：女性人數少于 49%，或多于 54%。不管發生那種情況，調查結果都會嚴重偏差。 假設專家告訴你，收入中位數是預測房價中位數非常重要的屬性。你可能想要保證測試集可以代表整體數據集中的多種收入分類。因為收入中位數是一個連續的數值屬性，你首先需要創建一個收入類別屬性。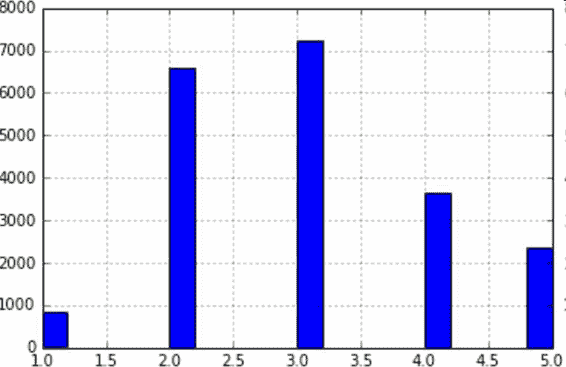再仔細地看一下收入中位數的柱狀圖（圖 2-9）（譯注：該圖是對收入中位數處理過后的圖）：  圖 2-9 收入分類的柱狀圖 大多數的收入中位數的值聚集在 2-5（萬美元），但是一些收入中位數會超過 6。數據集中的每個分層都要有足夠的實例位于你的數據中，這點很重要。否則，對分層重要性的評估就會有偏差。這意味著，你不能有過多的分層，且每個分層都要足夠大。后面的代碼通過將收入中位數除以 1.5（以限制收入分類的數量），創建了一個收入類別屬性，用`ceil`對值舍入（以產生離散的分類），然后將所有大于 5 的分類歸入到分類 5： ```python housing["income_cat"] = np.ceil(housing["median_income"] / 1.5) housing["income_cat"].where(housing["income_cat"] < 5, 5.0, inplace=True) ``` 現在，就可以根據收入分類，進行分層采樣。你可以使用 Scikit-Learn 的`StratifiedShuffleSplit`類： ```python from sklearn.model_selection import StratifiedShuffleSplit split = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42) for train_index, test_index in split.split(housing, housing["income_cat"]): strat_train_set = housing.loc[train_index] strat_test_set = housing.loc[test_index] ``` 檢查下結果是否符合預期。你可以在完整的房產數據集中查看收入分類比例： ```python >>> housing["income_cat"].value_counts() / len(housing) 3.0 0.350581 2.0 0.318847 4.0 0.176308 5.0 0.114438 1.0 0.039826 Name: income_cat, dtype: float64 ``` 使用相似的代碼，還可以測量測試集中收入分類的比例。圖 2-10 對比了總數據集、分層采樣的測試集、純隨機采樣測試集的收入分類比例。可以看到，分層采樣測試集的收入分類比例與總數據集幾乎相同，而隨機采樣數據集偏差嚴重。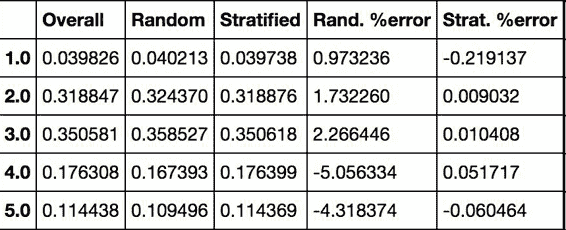  圖 2-10 分層采樣和純隨機采樣的樣本偏差比較 現在，你需要刪除`income_cat`屬性，使數據回到初始狀態： ```python for set in (strat_train_set, strat_test_set): set.drop(["income_cat"], axis=1, inplace=True) ``` 我們用了大量時間來生成測試集的原因是：測試集通常被忽略，但實際是機器學習非常重要的一部分。還有，生成測試集過程中的許多思路對于后面的交叉驗證討論是非常有幫助的。接下來進入下一階段：數據探索。 ## 數據探索和可視化、發現規律 目前為止，你只是快速查看了數據，對要處理的數據有了整體了解。現在的目標是更深的探索數據。 首先，保證你將測試集放在了一旁，只是研究訓練集。另外，如果訓練集非常大，你可能需要再采樣一個探索集，保證操作方便快速。在我們的案例中，數據集很小，所以可以在全集上直接工作。創建一個副本，以免損傷訓練集： ```python housing = strat_train_set.copy() ``` ### 地理數據可視化 因為存在地理信息（緯度和經度），創建一個所有街區的散點圖來數據可視化是一個不錯的主意（圖 2-11）： ```python housing.plot(kind="scatter", x="longitude", y="latitude") ```  圖 2-11 數據的地理信息散點圖 這張圖看起來很像加州，但是看不出什么特別的規律。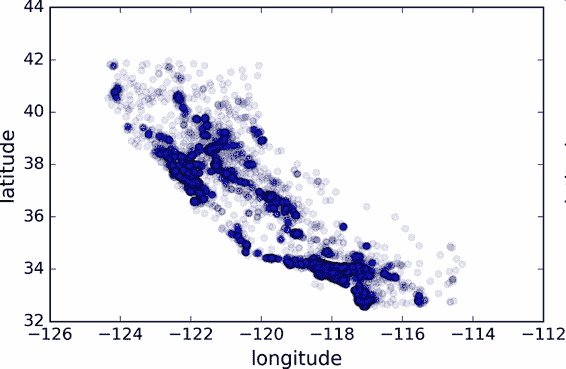將`alpha`設為 0.1，可以更容易看出數據點的密度（圖 2-12）： ```python housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.1) ```  圖 2-12 顯示高密度區域的散點圖 現在看起來好多了：可以非常清楚地看到高密度區域，灣區、洛杉磯和圣迭戈，以及中央谷，特別是從薩克拉門托和弗雷斯諾。 通常來講，人類的大腦非常善于發現圖片中的規律，但是需要調整可視化參數使規律顯現出來。 現在來看房價（圖 2-13）。每個圈的半徑表示街區的人口（選項`s`），顏色代表價格（選項`c`）。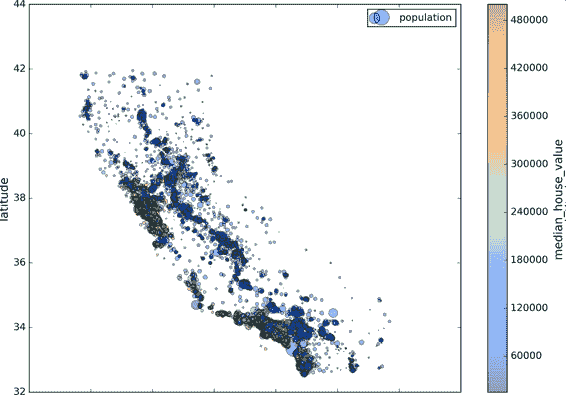我們用預先定義的名為`jet`的顏色圖（選項`cmap`），它的范圍是從藍色（低價）到紅色（高價）： ```python housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.4, s=housing["population"]/100, label="population", c="median_house_value", cmap=plt.get_cmap("jet"), colorbar=True, ) plt.legend() ```  圖 2-13 加州房價 這張圖說明房價和位置（比如，靠海）和人口密度聯系密切，這點你可能早就知道。可以使用聚類算法來檢測主要的聚集，用一個新的特征值測量聚集中心的距離。盡管北加州海岸區域的房價不是非常高，但離大海距離屬性也可能很有用，所以這不是用一個簡單的規則就可以定義的問題。 ### 查找關聯 因為數據集并不是非常大，你可以很容易地使用`corr()`方法計算出每對屬性間的標準相關系數（standard correlation coefficient，也稱作皮爾遜相關系數）： ```python corr_matrix = housing.corr() ``` 現在來看下每個屬性和房價中位數的關聯度： ```python >>> corr_matrix["median_house_value"].sort_values(ascending=False) median_house_value 1.000000 median_income 0.687170 total_rooms 0.135231 housing_median_age 0.114220 households 0.064702 total_bedrooms 0.047865 population -0.026699 longitude -0.047279 latitude -0.142826 Name: median_house_value, dtype: float64 ``` 相關系數的范圍是 -1 到 1。當接近 1 時，意味強正相關；例如，當收入中位數增加時，房價中位數也會增加。當相關系數接近 -1 時，意味強負相關；你可以看到，緯度和房價中位數有輕微的負相關性（即，越往北，房價越可能降低）。最后，相關系數接近 0，意味沒有線性相關性。圖 2-14 展示了相關系數在橫軸和縱軸之間的不同圖形。  圖 2-14 不同數據集的標準相關系數（來源：Wikipedia；公共領域圖片） > 警告：相關系數只測量線性關系（如果`x`上升，`y`則上升或下降）。相關系數可能會完全忽略非線性關系（例如，如果`x`接近 0，則`y`值會變高）。在上面圖片的最后一行中，他們的相關系數都接近于 0，盡管它們的軸并不獨立：這些就是非線性關系的例子。另外，第二行的相關系數等于 1 或 -1；這和斜率沒有任何關系。例如，你的身高（單位是英寸）與身高（單位是英尺或納米）的相關系數就是 1。 另一種檢測屬性間相關系數的方法是使用 Pandas 的`scatter_matrix`函數，它能畫出每個數值屬性對每個其它數值屬性的圖。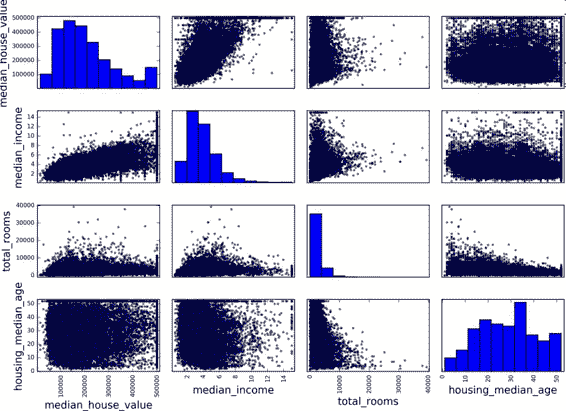因為現在共有 11 個數值屬性，你可以得到`11 ** 2 = 121`張圖，在一頁上畫不下，所以只關注幾個和房價中位數最有可能相關的屬性（圖 2-15）： ```python from pandas.tools.plotting import scatter_matrix attributes = ["median_house_value", "median_income", "total_rooms", "housing_median_age"] scatter_matrix(housing[attributes], figsize=(12, 8)) ```  圖 2-15 散點矩陣 如果 pandas 將每個變量對自己作圖，主對角線（左上到右下）都會是直線圖。所以 Pandas 展示的是每個屬性的柱狀圖（也可以是其它的，請參考 Pandas 文檔）。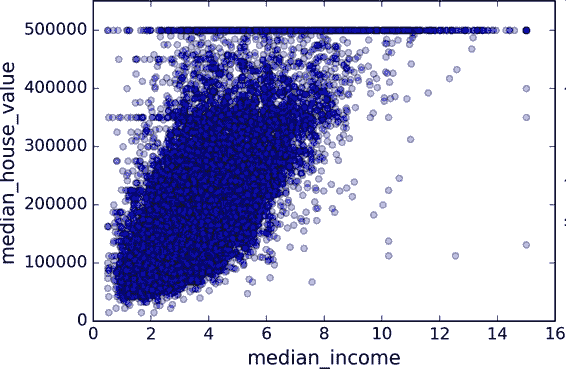 最有希望用來預測房價中位數的屬性是收入中位數，因此將這張圖放大（圖 2-16）： ```python housing.plot(kind="scatter", x="median_income",y="median_house_value", alpha=0.1) ```  圖 2-16 收入中位數 vs 房價中位數 這張圖說明了幾點。首先，相關性非常高；可以清晰地看到向上的趨勢，并且數據點不是非常分散。第二，我們之前看到的最高價，清晰地呈現為一條位于 500000 美元的水平線。這張圖也呈現了一些不是那么明顯的直線：一條位于 450000 美元的直線，一條位于 350000 美元的直線，一條在 280000 美元的線，和一些更靠下的線。你可能希望去除對應的街區，以防止算法重復這些巧合。 ### 屬性組合試驗 希望前面的一節能教給你一些探索數據、發現規律的方法。你發現了一些數據的巧合，需要在給算法提供數據之前，將其去除。你還發現了一些屬性間有趣的關聯，特別是目標屬性。你還注意到一些屬性具有長尾分布，因此你可能要將其進行轉換（例如，計算其`log`對數）。當然，不同項目的處理方法各不相同，但大體思路是相似的。 給算法準備數據之前，你需要做的最后一件事是嘗試多種屬性組合。例如，如果你不知道某個街區有多少戶，該街區的總房間數就沒什么用。你真正需要的是每戶有幾個房間。相似的，總臥室數也不重要：你可能需要將其與房間數進行比較。每戶的人口數也是一個有趣的屬性組合。讓我們來創建這些新的屬性： ```python housing["rooms_per_household"] = housing["total_rooms"]/housing["households"] housing["bedrooms_per_room"] = housing["total_bedrooms"]/housing["total_rooms"] housing["population_per_household"]=housing["population"]/housing["households"] ``` 現在，再來看相關矩陣： ```python >>> corr_matrix = housing.corr() >>> corr_matrix["median_house_value"].sort_values(ascending=False) median_house_value 1.000000 median_income 0.687170 rooms_per_household 0.199343 total_rooms 0.135231 housing_median_age 0.114220 households 0.064702 total_bedrooms 0.047865 population_per_household -0.021984 population -0.026699 longitude -0.047279 latitude -0.142826 bedrooms_per_room -0.260070 Name: median_house_value, dtype: float64 ``` 看起來不錯！與總房間數或臥室數相比，新的`bedrooms_per_room`屬性與房價中位數的關聯更強。顯然，臥室數/總房間數的比例越低，房價就越高。每戶的房間數也比街區的總房間數的更有信息，很明顯，房屋越大，房價就越高。 這一步的數據探索不必非常完備，此處的目的是有一個正確的開始，快速發現規律，以得到一個合理的原型。但是這是一個交互過程：一旦你得到了一個原型，并運行起來，你就可以分析它的輸出，進而發現更多的規律，然后再回到數據探索這步。 ## 為機器學習算法準備數據 現在來為機器學習算法準備數據。不要手工來做，你需要寫一些函數，理由如下： + 函數可以讓你在任何數據集上（比如，你下一次獲取的是一個新的數據集）方便地進行重復數據轉換。 + 你能慢慢建立一個轉換函數庫，可以在未來的項目中復用。 + 在將數據傳給算法之前，你可以在實時系統中使用這些函數。 + 這可以讓你方便地嘗試多種數據轉換，查看哪些轉換方法結合起來效果最好。 但是，還是先回到干凈的訓練集（通過再次復制`strat_train_set`），將預測量和標簽分開，因為我們不想對預測量和目標值應用相同的轉換（注意`drop()`創建了一份數據的備份，而不影響`strat_train_set`）： ```python housing = strat_train_set.drop("median_house_value", axis=1) housing_labels = strat_train_set["median_house_value"].copy() ``` ### 數據清洗 大多機器學習算法不能處理缺失的特征，因此先創建一些函數來處理特征缺失的問題。前面，你應該注意到了屬性`total_bedrooms`有一些缺失值。有三個解決選項： + 去掉對應的街區； + 去掉整個屬性； + 進行賦值（0、平均值、中位數等等）。 用`DataFrame`的`dropna()`，`drop()`，和`fillna()`方法，可以方便地實現： ```python housing.dropna(subset=["total_bedrooms"]) # 選項 1 housing.drop("total_bedrooms", axis=1) # 選項 2 median = housing["total_bedrooms"].median() housing["total_bedrooms"].fillna(median) # 選項 3 ``` 如果選擇選項 3，你需要計算訓練集的中位數，用中位數填充訓練集的缺失值，不要忘記保存該中位數。后面用測試集評估系統時，需要替換測試集中的缺失值，也可以用來實時替換新數據中的缺失值。 Scikit-Learn 提供了一個方便的類來處理缺失值：`Imputer`。下面是其使用方法：首先，需要創建一個`Imputer`實例，指定用某屬性的中位數來替換該屬性所有的缺失值： ```python from sklearn.preprocessing import Imputer imputer = Imputer(strategy="median") ``` 因為只有數值屬性才能算出中位數，我們需要創建一份不包括文本屬性`ocean_proximity`的數據副本： ```python housing_num = housing.drop("ocean_proximity", axis=1) ``` 現在，就可以用`fit()`方法將`imputer`實例擬合到訓練數據： ```python imputer.fit(housing_num) ``` `imputer`計算出了每個屬性的中位數，并將結果保存在了實例變量`statistics_`中。雖然此時只有屬性`total_bedrooms`存在缺失值，但我們不能確定在以后的新的數據中會不會有其他屬性也存在缺失值，所以安全的做法是將`imputer`應用到每個數值： ```python >>> imputer.statistics_ array([ -118.51 , 34.26 , 29. , 2119. , 433. , 1164. , 408. , 3.5414]) >>> housing_num.median().values array([ -118.51 , 34.26 , 29. , 2119. , 433. , 1164. , 408. , 3.5414]) ``` 現在，你就可以使用這個“訓練過的”`imputer`來對訓練集進行轉換，將缺失值替換為中位數： ```python X = imputer.transform(housing_num) ``` 結果是一個包含轉換后特征的普通的 Numpy 數組。如果你想將其放回到 Pandas`DataFrame`中，也很簡單： ```python housing_tr = pd.DataFrame(X, columns=housing_num.columns) ``` > Scikit-Learn 設計 > > Scikit-Learn 設計的 API 設計的非常好。它的主要設計原則是： > > + 一致性：所有對象的接口一致且簡單： > > + 估計器（estimator）。任何可以基于數據集對一些參數進行估計的對象都被稱為估計器（比如，`imputer`就是個估計器）。估計本身是通過`fit()`方法，只需要一個數據集作為參數（對于監督學習算法，需要兩個數據集；第二個數據集包含標簽）。任何其它用來指導估計過程的參數都被當做超參數（比如`imputer`的`strategy`），并且超參數要被設置成實例變量（通常通過構造器參數設置）。 > + 轉換器（transformer）。一些估計器（比如`imputer`）也可以轉換數據集，這些估計器被稱為轉換器。API 也是相當簡單：轉換是通過`transform()`方法，被轉換的數據集作為參數。返回的是經過轉換的數據集。轉換過程依賴學習到的參數，比如`imputer`的例子。所有的轉換都有一個便捷的方法`fit_transform()`，等同于調用`fit()`再`transform()`（但有時`fit_transform()`經過優化，運行的更快）。 > + 預測器（predictor）。最后，一些估計器可以根據給出的數據集做預測，這些估計器稱為預測器。例如，上一章的`LinearRegression`模型就是一個預測器：它根據一個國家的人均 GDP 預測生活滿意度。預測器有一個`predict()`方法，可以用新實例的數據集做出相應的預測。預測器還有一個`score()`方法，可用于評估測試集（如果是監督學習算法的話，還要給出相應的標簽）的預測質量。 > > + 可檢驗。所有估計器的超參數都可以通過實例的 public 變量直接訪問（比如，`imputer.strategy`），并且所有估計器學習到的參數也可以通過在實例變量名后加下劃線來訪問（比如，`imputer.statistics_`）。 > > + 類不可擴散。數據集被表示成 NumPy 數組或 SciPy 稀疏矩陣，而不是自制的類。超參數只是普通的 Python 字符串或數字。 > > + 可組合。盡可能使用現存的模塊。例如，用任意的轉換器序列加上一個估計器，就可以做成一個流水線，后面會看到例子。 > > + 合理的默認值。Scikit-Learn 給大多數參數提供了合理的默認值，很容易就能創建一個系統。 ### 處理文本和類別屬性 前面，我們丟棄了類別屬性`ocean_proximity`，因為它是一個文本屬性，不能計算出中位數。大多數機器學習算法更喜歡和數字打交道，所以讓我們把這些文本標簽轉換為數字。 Scikit-Learn 為這個任務提供了一個轉換器`LabelEncoder`： ```python >>> from sklearn.preprocessing import LabelEncoder >>> encoder = LabelEncoder() >>> housing_cat = housing["ocean_proximity"] >>> housing_cat_encoded = encoder.fit_transform(housing_cat) >>> housing_cat_encoded array([1, 1, 4, ..., 1, 0, 3]) ``` > 譯注: > > 在原書中使用`LabelEncoder`轉換器來轉換文本特征列的方式是錯誤的，該轉換器只能用來轉換標簽（正如其名）。在這里使用`LabelEncoder`沒有出錯的原因是該數據只有一列文本特征值，在有多個文本特征列的時候就會出錯。應使用`factorize()`方法來進行操作： > > ```python > housing_cat_encoded, housing_categories = housing_cat.factorize() > housing_cat_encoded[:10] > ``` 好了一些，現在就可以在任何 ML 算法里用這個數值數據了。你可以查看映射表，編碼器是通過屬性`classes_`來學習的（`<1H OCEAN`被映射為 0，`INLAND`被映射為 1，等等）： ```python >>> print(encoder.classes_) ['<1H OCEAN' 'INLAND' 'ISLAND' 'NEAR BAY' 'NEAR OCEAN'] ``` 這種做法的問題是，ML 算法會認為兩個臨近的值比兩個疏遠的值要更相似。顯然這樣不對（比如，分類 0 和分類 4 就比分類 0 和分類 1 更相似）。要解決這個問題，一個常見的方法是給每個分類創建一個二元屬性：當分類是`<1H OCEAN`，該屬性為 1（否則為 0），當分類是`INLAND`，另一個屬性等于 1（否則為 0），以此類推。這稱作獨熱編碼（One-Hot Encoding），因為只有一個屬性會等于 1（熱），其余會是 0（冷）。 Scikit-Learn 提供了一個編碼器`OneHotEncoder`，用于將整數分類值轉變為獨熱向量。注意`fit_transform()`用于 2D 數組，而`housing_cat_encoded`是一個 1D 數組，所以需要將其變形： ```python >>> from sklearn.preprocessing import OneHotEncoder >>> encoder = OneHotEncoder() >>> housing_cat_1hot = encoder.fit_transform(housing_cat_encoded.reshape(-1,1)) >>> housing_cat_1hot <16513x5 sparse matrix of type '<class 'numpy.float64'>' with 16513 stored elements in Compressed Sparse Row format> ``` 注意輸出結果是一個 SciPy 稀疏矩陣，而不是 NumPy 數組。當類別屬性有數千個分類時，這樣非常有用。經過獨熱編碼，我們得到了一個有數千列的矩陣，這個矩陣每行只有一個 1，其余都是 0。使用大量內存來存儲這些 0 非常浪費，所以稀疏矩陣只存儲非零元素的位置。你可以像一個 2D 數據那樣進行使用，但是如果你真的想將其轉變成一個（密集的）NumPy 數組，只需調用`toarray()`方法： ```python >>> housing_cat_1hot.toarray() array([[ 0., 1., 0., 0., 0.], [ 0., 1., 0., 0., 0.], [ 0., 0., 0., 0., 1.], ..., [ 0., 1., 0., 0., 0.], [ 1., 0., 0., 0., 0.], [ 0., 0., 0., 1., 0.]]) ``` 使用類`LabelBinarizer`，我們可以用一步執行這兩個轉換（從文本分類到整數分類，再從整數分類到獨熱向量）： ```python >>> from sklearn.preprocessing import LabelBinarizer >>> encoder = LabelBinarizer() >>> housing_cat_1hot = encoder.fit_transform(housing_cat) >>> housing_cat_1hot array([[0, 1, 0, 0, 0], [0, 1, 0, 0, 0], [0, 0, 0, 0, 1], ..., [0, 1, 0, 0, 0], [1, 0, 0, 0, 0], [0, 0, 0, 1, 0]]) ``` 注意默認返回的結果是一個密集 NumPy 數組。向構造器`LabelBinarizer`傳遞`sparse_output=True`，就可以得到一個稀疏矩陣。 > 譯注: > > 在原書中使用`LabelBinarizer`的方式也是錯誤的，該類也應用于標簽列的轉換。正確做法是使用 sklearn 即將提供的`CategoricalEncoder`類。如果在你閱讀此文時 sklearn 中尚未提供此類，用如下方式代替：（來自[Pull Request #9151）](https://github.com/scikit-learn/scikit-learn/pull/9151) > > ```python > # Definition of the CategoricalEncoder class, copied from PR #9151. > # Just run this cell, or copy it to your code, do not try to understand it (yet). > > from sklearn.base import BaseEstimator, TransformerMixin > from sklearn.utils import check_array > from sklearn.preprocessing import LabelEncoder > from scipy import sparse > > class CategoricalEncoder(BaseEstimator, TransformerMixin): > """Encode categorical features as a numeric array. > The input to this transformer should be a matrix of integers or strings, > denoting the values taken on by categorical (discrete) features. > The features can be encoded using a one-hot aka one-of-K scheme > (``encoding='onehot'``, the default) or converted to ordinal integers > (``encoding='ordinal'``). > This encoding is needed for feeding categorical data to many scikit-learn > estimators, notably linear models and SVMs with the standard kernels. > Read more in the :ref:`User Guide <preprocessing_categorical_features>`. > Parameters > ---------- > encoding : str, 'onehot', 'onehot-dense' or 'ordinal' > The type of encoding to use (default is 'onehot'): > - 'onehot': encode the features using a one-hot aka one-of-K scheme > (or also called 'dummy' encoding). This creates a binary column for > each category and returns a sparse matrix. > - 'onehot-dense': the same as 'onehot' but returns a dense array > instead of a sparse matrix. > - 'ordinal': encode the features as ordinal integers. This results in > a single column of integers (0 to n_categories - 1) per feature. > categories : 'auto' or a list of lists/arrays of values. > Categories (unique values) per feature: > - 'auto' : Determine categories automatically from the training data. > - list : ``categories[i]`` holds the categories expected in the ith > column. The passed categories are sorted before encoding the data > (used categories can be found in the ``categories_`` attribute). > dtype : number type, default np.float64 > Desired dtype of output. > handle_unknown : 'error' (default) or 'ignore' > Whether to raise an error or ignore if a unknown categorical feature is > present during transform (default is to raise). When this is parameter > is set to 'ignore' and an unknown category is encountered during > transform, the resulting one-hot encoded columns for this feature > will be all zeros. > Ignoring unknown categories is not supported for > ``encoding='ordinal'``. > Attributes > ---------- > categories_ : list of arrays > The categories of each feature determined during fitting. When > categories were specified manually, this holds the sorted categories > (in order corresponding with output of `transform`). > Examples > -------- > Given a dataset with three features and two samples, we let the encoder > find the maximum value per feature and transform the data to a binary > one-hot encoding. > >>> from sklearn.preprocessing import CategoricalEncoder > >>> enc = CategoricalEncoder(handle_unknown='ignore') > >>> enc.fit([[0, 0, 3], [1, 1, 0], [0, 2, 1], [1, 0, 2]]) > ... # doctest: +ELLIPSIS > CategoricalEncoder(categories='auto', dtype=<... 'numpy.float64'>, > encoding='onehot', handle_unknown='ignore') > >>> enc.transform([[0, 1, 1], [1, 0, 4]]).toarray() > array([[ 1., 0., 0., 1., 0., 0., 1., 0., 0.], > [ 0., 1., 1., 0., 0., 0., 0., 0., 0.]]) > See also > -------- > sklearn.preprocessing.OneHotEncoder : performs a one-hot encoding of > integer ordinal features. The ``OneHotEncoder assumes`` that input > features take on values in the range ``[0, max(feature)]`` instead of > using the unique values. > sklearn.feature_extraction.DictVectorizer : performs a one-hot encoding of > dictionary items (also handles string-valued features). > sklearn.feature_extraction.FeatureHasher : performs an approximate one-hot > encoding of dictionary items or strings. > """ > > def __init__(self, encoding='onehot', categories='auto', dtype=np.float64, > handle_unknown='error'): > self.encoding = encoding > self.categories = categories > self.dtype = dtype > self.handle_unknown = handle_unknown > > def fit(self, X, y=None): > """Fit the CategoricalEncoder to X. > Parameters > ---------- > X : array-like, shape [n_samples, n_feature] > The data to determine the categories of each feature. > Returns > ------- > self > """ > > if self.encoding not in ['onehot', 'onehot-dense', 'ordinal']: > template = ("encoding should be either 'onehot', 'onehot-dense' " > "or 'ordinal', got %s") > raise ValueError(template % self.handle_unknown) > > if self.handle_unknown not in ['error', 'ignore']: > template = ("handle_unknown should be either 'error' or " > "'ignore', got %s") > raise ValueError(template % self.handle_unknown) > > if self.encoding == 'ordinal' and self.handle_unknown == 'ignore': > raise ValueError("handle_unknown='ignore' is not supported for" > " encoding='ordinal'") > > X = check_array(X, dtype=np.object, accept_sparse='csc', copy=True) > n_samples, n_features = X.shape > > self._label_encoders_ = [LabelEncoder() for _ in range(n_features)] > > for i in range(n_features): > le = self._label_encoders_[i] > Xi = X[:, i] > if self.categories == 'auto': > le.fit(Xi) > else: > valid_mask = np.in1d(Xi, self.categories[i]) > if not np.all(valid_mask): > if self.handle_unknown == 'error': > diff = np.unique(Xi[~valid_mask]) > msg = ("Found unknown categories {0} in column {1}" > " during fit".format(diff, i)) > raise ValueError(msg) > le.classes_ = np.array(np.sort(self.categories[i])) > > self.categories_ = [le.classes_ for le in self._label_encoders_] > > return self > > def transform(self, X): > """Transform X using one-hot encoding. > Parameters > ---------- > X : array-like, shape [n_samples, n_features] > The data to encode. > Returns > ------- > X_out : sparse matrix or a 2-d array > Transformed input. > """ > X = check_array(X, accept_sparse='csc', dtype=np.object, copy=True) > n_samples, n_features = X.shape > X_int = np.zeros_like(X, dtype=np.int) > X_mask = np.ones_like(X, dtype=np.bool) > > for i in range(n_features): > valid_mask = np.in1d(X[:, i], self.categories_[i]) > > if not np.all(valid_mask): > if self.handle_unknown == 'error': > diff = np.unique(X[~valid_mask, i]) > msg = ("Found unknown categories {0} in column {1}" > " during transform".format(diff, i)) > raise ValueError(msg) > else: > # Set the problematic rows to an acceptable value and > # continue `The rows are marked `X_mask` and will be > # removed later. > X_mask[:, i] = valid_mask > X[:, i][~valid_mask] = self.categories_[i][0] > X_int[:, i] = self._label_encoders_[i].transform(X[:, i]) > > if self.encoding == 'ordinal': > return X_int.astype(self.dtype, copy=False) > > mask = X_mask.ravel() > n_values = [cats.shape[0] for cats in self.categories_] > n_values = np.array([0] + n_values) > indices = np.cumsum(n_values) > > column_indices = (X_int + indices[:-1]).ravel()[mask] > row_indices = np.repeat(np.arange(n_samples, dtype=np.int32), > n_features)[mask] > data = np.ones(n_samples * n_features)[mask] > > out = sparse.csc_matrix((data, (row_indices, column_indices)), > shape=(n_samples, indices[-1]), > dtype=self.dtype).tocsr() > if self.encoding == 'onehot-dense': > return out.toarray() > else: > return out > ``` > > 轉換方法： > > ```python > #from sklearn.preprocessing import CategoricalEncoder # in future versions of Scikit-Learn > > cat_encoder = CategoricalEncoder() > housing_cat_reshaped = housing_cat.values.reshape(-1, 1) > housing_cat_1hot = cat_encoder.fit_transform(housing_cat_reshaped) > housing_cat_1hot > ``` ### 自定義轉換器 盡管 Scikit-Learn 提供了許多有用的轉換器，你還是需要自己動手寫轉換器執行任務，比如自定義的清理操作，或屬性組合。你需要讓自制的轉換器與 Scikit-Learn 組件（比如流水線）無縫銜接工作，因為 Scikit-Learn 是依賴鴨子類型的（而不是繼承），你所需要做的是創建一個類并執行三個方法：`fit()`（返回`self`），`transform()`，和`fit_transform()`。通過添加`TransformerMixin`作為基類，可以很容易地得到最后一個。另外，如果你添加`BaseEstimator`作為基類（且構造器中避免使用`*args`和`**kargs`），你就能得到兩個額外的方法（`get_params() `和`set_params()`），二者可以方便地進行超參數自動微調。例如，一個小轉換器類添加了上面討論的屬性： ```python from sklearn.base import BaseEstimator, TransformerMixin rooms_ix, bedrooms_ix, population_ix, household_ix = 3, 4, 5, 6 class CombinedAttributesAdder(BaseEstimator, TransformerMixin): def __init__(self, add_bedrooms_per_room = True): # no *args or **kargs self.add_bedrooms_per_room = add_bedrooms_per_room def fit(self, X, y=None): return self # nothing else to do def transform(self, X, y=None): rooms_per_household = X[:, rooms_ix] / X[:, household_ix] population_per_household = X[:, population_ix] / X[:, household_ix] if self.add_bedrooms_per_room: bedrooms_per_room = X[:, bedrooms_ix] / X[:, rooms_ix] return np.c_[X, rooms_per_household, population_per_household, bedrooms_per_room] else: return np.c_[X, rooms_per_household, population_per_household] attr_adder = CombinedAttributesAdder(add_bedrooms_per_room=False) housing_extra_attribs = attr_adder.transform(housing.values) ``` 在這個例子中，轉換器有一個超參數`add_bedrooms_per_room`，默認設為`True`（提供一個合理的默認值很有幫助）。這個超參數可以讓你方便地發現添加了這個屬性是否對機器學習算法有幫助。更一般地，你可以為每個不能完全確保的數據準備步驟添加一個超參數。數據準備步驟越自動化，可以自動化的操作組合就越多，越容易發現更好用的組合（并能節省大量時間）。 ### 特征縮放 數據要做的最重要的轉換之一是特征縮放。除了個別情況，當輸入的數值屬性量度不同時，機器學習算法的性能都不會好。這個規律也適用于房產數據：總房間數分布范圍是 6 到 39320，而收入中位數只分布在 0 到 15。注意通常情況下我們不需要對目標值進行縮放。 有兩種常見的方法可以讓所有的屬性有相同的量度：線性函數歸一化（Min-Max scaling）和標準化（standardization）。 線性函數歸一化（許多人稱其為歸一化（normalization））很簡單：值被轉變、重新縮放，直到范圍變成 0 到 1。我們通過減去最小值，然后再除以最大值與最小值的差值，來進行歸一化。Scikit-Learn 提供了一個轉換器`MinMaxScaler`來實現這個功能。它有一個超參數`feature_range`，可以讓你改變范圍，如果不希望范圍是 0 到 1。 標準化就很不同：首先減去平均值（所以標準化值的平均值總是 0），然后除以方差，使得到的分布具有單位方差。與歸一化不同，標準化不會限定值到某個特定的范圍，這對某些算法可能構成問題（比如，神經網絡常需要輸入值得范圍是 0 到 1）。但是，標準化受到異常值的影響很小。例如，假設一個街區的收入中位數由于某種錯誤變成了 100，歸一化會將其它范圍是 0 到 15 的值變為 0-0.15，但是標準化不會受什么影響。Scikit-Learn 提供了一個轉換器`StandardScaler`來進行標準化。 > 警告：與所有的轉換一樣，縮放器只能向訓練集擬合，而不是向完整的數據集（包括測試集）。只有這樣，你才能用縮放器轉換訓練集和測試集（和新數據）。 ### 轉換流水線 你已經看到，存在許多數據轉換步驟，需要按一定的順序執行。幸運的是，Scikit-Learn 提供了類`Pipeline`，來進行這一系列的轉換。下面是一個數值屬性的小流水線： ```python from sklearn.pipeline import Pipeline from sklearn.preprocessing import StandardScaler num_pipeline = Pipeline([ ('imputer', Imputer(strategy="median")), ('attribs_adder', CombinedAttributesAdder()), ('std_scaler', StandardScaler()), ]) housing_num_tr = num_pipeline.fit_transform(housing_num) ``` `Pipeline`構造器需要一個定義步驟順序的名字/估計器對的列表。除了最后一個估計器，其余都要是轉換器（即，它們都要有`fit_transform()`方法）。名字可以隨意起。 當你調用流水線的`fit()`方法，就會對所有轉換器順序調用`fit_transform()`方法，將每次調用的輸出作為參數傳遞給下一個調用，一直到最后一個估計器，它只執行`fit()`方法。 流水線暴露相同的方法作為最終的估計器。在這個例子中，最后的估計器是一個`StandardScaler`，它是一個轉換器，因此這個流水線有一個`transform()`方法，可以順序對數據做所有轉換（它還有一個`fit_transform`方法可以使用，就不必先調用`fit()`再進行`transform()`）。 如果不需要手動將 Pandas`DataFrame`中的數值列轉成 Numpy 數組的格式，而可以直接將`DataFrame`輸入 pipeline 中進行處理就好了。Scikit-Learn 沒有工具來處理 Pandas`DataFrame`，因此我們需要寫一個簡單的自定義轉換器來做這項工作： ```python from sklearn.base import BaseEstimator, TransformerMixin class DataFrameSelector(BaseEstimator, TransformerMixin): def __init__(self, attribute_names): self.attribute_names = attribute_names def fit(self, X, y=None): return self def transform(self, X): return X[self.attribute_names].values ``` 每個子流水線都以一個選擇轉換器開始：通過選擇對應的屬性（數值或分類）、丟棄其它的，來轉換數據，并將輸出`DataFrame`轉變成一個 NumPy 數組。這樣，你就可以很簡單的寫出一個以 Pandas`DataFrame`為輸入并且可以處理數值的流水線： 該流水線從`DataFrameSelector`開始獲取數值屬性，前面討論過的其他數據處理步驟緊隨其后。 并且你也可以通過使用`DataFrameSelector`選擇類別屬性并為其寫另一個流水線然后應用`LabelBinarizer`. 你現在就有了一個對數值的流水線，你還需要對分類值應用`LabelBinarizer`：如何將這些轉換寫成一個流水線呢？Scikit-Learn 提供了一個類`FeatureUnion`實現這個功能。你給它一列轉換器（可以是所有的轉換器），當調用它的`transform()`方法，每個轉換器的`transform()`會被并行執行，等待輸出，然后將輸出合并起來，并返回結果（當然，調用它的`fit()`方法就會調用每個轉換器的`fit()`）。一個完整的處理數值和類別屬性的流水線如下所示： ```python from sklearn.pipeline import FeatureUnion num_attribs = list(housing_num) cat_attribs = ["ocean_proximity"] num_pipeline = Pipeline([ ('selector', DataFrameSelector(num_attribs)), ('imputer', Imputer(strategy="median")), ('attribs_adder', CombinedAttributesAdder()), ('std_scaler', StandardScaler()), ]) cat_pipeline = Pipeline([ ('selector', DataFrameSelector(cat_attribs)), ('label_binarizer', LabelBinarizer()), ]) full_pipeline = FeatureUnion(transformer_list=[ ("num_pipeline", num_pipeline), ("cat_pipeline", cat_pipeline), ]) ``` > 譯注: > > 如果你在上面代碼中的`cat_pipeline`流水線使用`LabelBinarizer`轉換器會導致執行錯誤，解決方案是用上文提到的`CategoricalEncoder`轉換器來代替： > > ```python > cat_pipeline = Pipeline([ > ('selector', DataFrameSelector(cat_attribs)), > ('cat_encoder', CategoricalEncoder(encoding="onehot-dense")), > ]) > ``` 你可以很簡單地運行整個流水線： ```python >>> housing_prepared = full_pipeline.fit_transform(housing) >>> housing_prepared array([[ 0.73225807, -0.67331551, 0.58426443, ..., 0. , 0. , 0. ], [-0.99102923, 1.63234656, -0.92655887, ..., 0. , 0. , 0. ], [...] >>> housing_prepared.shape (16513, 17) ``` ## 選擇并訓練模型 可到這一步了！你在前面限定了問題、獲得了數據、探索了數據、采樣了一個測試集、寫了自動化的轉換流水線來清理和為算法準備數據。現在，你已經準備好選擇并訓練一個機器學習模型了。 ### 在訓練集上訓練和評估 好消息是基于前面的工作，接下來要做的比你想的要簡單許多。像前一章那樣，我們先來訓練一個線性回歸模型： ```python from sklearn.linear_model import LinearRegression lin_reg = LinearRegression() lin_reg.fit(housing_prepared, housing_labels) ``` 完畢！你現在就有了一個可用的線性回歸模型。用一些訓練集中的實例做下驗證： ```python >>> some_data = housing.iloc[:5] >>> some_labels = housing_labels.iloc[:5] >>> some_data_prepared = full_pipeline.transform(some_data) >>> print("Predictions:\t", lin_reg.predict(some_data_prepared)) Predictions: [ 303104. 44800. 308928. 294208. 368704.] >>> print("Labels:\t\t", list(some_labels)) Labels: [359400.0, 69700.0, 302100.0, 301300.0, 351900.0] ``` 行的通，盡管預測并不怎么準確（比如，第二個預測偏離了 50%！）。讓我們使用 Scikit-Learn 的`mean_squared_error`函數，用全部訓練集來計算下這個回歸模型的 RMSE： ```python >>> from sklearn.metrics import mean_squared_error >>> housing_predictions = lin_reg.predict(housing_prepared) >>> lin_mse = mean_squared_error(housing_labels, housing_predictions) >>> lin_rmse = np.sqrt(lin_mse) >>> lin_rmse 68628.413493824875 ``` OK，有總比沒有強，但顯然結果并不好：大多數街區的`median_housing_values`位于 120000 到 265000 美元之間，因此預測誤差 68628 美元不能讓人滿意。這是一個模型欠擬合訓練數據的例子。當這種情況發生時，意味著特征沒有提供足夠多的信息來做出一個好的預測，或者模型并不強大。就像前一章看到的，修復欠擬合的主要方法是選擇一個更強大的模型，給訓練算法提供更好的特征，或去掉模型上的限制。這個模型還沒有正則化，所以排除了最后一個選項。你可以嘗試添加更多特征（比如，人口的對數值），但是首先讓我們嘗試一個更為復雜的模型，看看效果。 來訓練一個`DecisionTreeRegressor`。這是一個強大的模型，可以發現數據中復雜的非線性關系（決策樹會在第 6 章詳細講解）。代碼看起來很熟悉： ```python from sklearn.tree import DecisionTreeRegressor tree_reg = DecisionTreeRegressor() tree_reg.fit(housing_prepared, housing_labels) ``` 現在模型就訓練好了，用訓練集評估下： ```python >>> housing_predictions = tree_reg.predict(housing_prepared) >>> tree_mse = mean_squared_error(housing_labels, housing_predictions) >>> tree_rmse = np.sqrt(tree_mse) >>> tree_rmse 0.0 ``` 等一下，發生了什么？沒有誤差？這個模型可能是絕對完美的嗎？當然，更大可能性是這個模型嚴重過擬合數據。如何確定呢？如前所述，直到你準備運行一個具備足夠信心的模型，都不要碰測試集，因此你需要使用訓練集的部分數據來做訓練，用一部分來做模型驗證。 ### 使用交叉驗證做更佳的評估 評估決策樹模型的一種方法是用函數`train_test_split`來分割訓練集，得到一個更小的訓練集和一個驗證集，然后用更小的訓練集來訓練模型，用驗證集來評估。這需要一定工作量，并不難而且也可行。 另一種更好的方法是使用 Scikit-Learn 的交叉驗證功能。下面的代碼采用了 K 折交叉驗證（K-fold cross-validation）：它隨機地將訓練集分成十個不同的子集，成為“折”，然后訓練評估決策樹模型 10 次，每次選一個不用的折來做評估，用其它 9 個來做訓練。結果是一個包含 10 個評分的數組： ```python from sklearn.model_selection import cross_val_score scores = cross_val_score(tree_reg, housing_prepared, housing_labels, scoring="neg_mean_squared_error", cv=10) tree_rmse_scores = np.sqrt(-scores) ``` > 警告：Scikit-Learn 交叉驗證功能期望的是效用函數（越大越好）而不是損失函數（越低越好），因此得分函數實際上與 MSE 相反（即負值），這就是為什么前面的代碼在計算平方根之前先計算`-scores`。 來看下結果： ```python >>> def display_scores(scores): ... print("Scores:", scores) ... print("Mean:", scores.mean()) ... print("Standard deviation:", scores.std()) ... >>> display_scores(tree_rmse_scores) Scores: [ 74678.4916885 64766.2398337 69632.86942005 69166.67693232 71486.76507766 73321.65695983 71860.04741226 71086.32691692 76934.2726093 69060.93319262] Mean: 71199.4280043 Standard deviation: 3202.70522793 ``` 現在決策樹就不像前面看起來那么好了。實際上，它看起來比線性回歸模型還糟！注意到交叉驗證不僅可以讓你得到模型性能的評估，還能測量評估的準確性（即，它的標準差）。決策樹的評分大約是 71200，通常波動有 ±3200。如果只有一個驗證集，就得不到這些信息。但是交叉驗證的代價是訓練了模型多次，不可能總是這樣。 讓我們計算下線性回歸模型的的相同分數，以做確保： ```python >>> lin_scores = cross_val_score(lin_reg, housing_prepared, housing_labels, ... scoring="neg_mean_squared_error", cv=10) ... >>> lin_rmse_scores = np.sqrt(-lin_scores) >>> display_scores(lin_rmse_scores) Scores: [ 70423.5893262 65804.84913139 66620.84314068 72510.11362141 66414.74423281 71958.89083606 67624.90198297 67825.36117664 72512.36533141 68028.11688067] Mean: 68972.377566 Standard deviation: 2493.98819069 ``` 判斷沒錯：決策樹模型過擬合很嚴重，它的性能比線性回歸模型還差。 現在再嘗試最后一個模型：`RandomForestRegressor`。第 7 章我們會看到，隨機森林是通過用特征的隨機子集訓練許多決策樹。在其它多個模型之上建立模型稱為集成學習（Ensemble Learning），它是推進 ML 算法的一種好方法。我們會跳過大部分的代碼，因為代碼本質上和其它模型一樣： ```python >>> from sklearn.ensemble import RandomForestRegressor >>> forest_reg = RandomForestRegressor() >>> forest_reg.fit(housing_prepared, housing_labels) >>> [...] >>> forest_rmse 22542.396440343684 >>> display_scores(forest_rmse_scores) Scores: [ 53789.2879722 50256.19806622 52521.55342602 53237.44937943 52428.82176158 55854.61222549 52158.02291609 50093.66125649 53240.80406125 52761.50852822] Mean: 52634.1919593 Standard deviation: 1576.20472269 ``` 現在好多了：隨機森林看起來很有希望。但是，訓練集的評分仍然比驗證集的評分低很多。解決過擬合可以通過簡化模型，給模型加限制（即，規整化），或用更多的訓練數據。在深入隨機森林之前，你應該嘗試下機器學習算法的其它類型模型（不同核心的支持向量機，神經網絡，等等），不要在調節超參數上花費太多時間。目標是列出一個可能模型的列表（兩到五個）。 > 提示：你要保存每個試驗過的模型，以便后續可以再用。要確保有超參數和訓練參數，以及交叉驗證評分，和實際的預測值。這可以讓你比較不同類型模型的評分，還可以比較誤差種類。你可以用 Python 的模塊`pickle`，非常方便地保存 Scikit-Learn 模型，或使用`sklearn.externals.joblib`，后者序列化大 NumPy 數組更有效率： > ```python > from sklearn.externals import joblib > > joblib.dump(my_model, "my_model.pkl") > # 然后 > my_model_loaded = joblib.load("my_model.pkl") > ``` ## 模型微調 假設你現在有了一個列表，列表里有幾個有希望的模型。你現在需要對它們進行微調。讓我們來看幾種微調的方法。 ### 網格搜索 微調的一種方法是手工調整超參數，直到找到一個好的超參數組合。這么做的話會非常冗長，你也可能沒有時間探索多種組合。 你應該使用 Scikit-Learn 的`GridSearchCV`來做這項搜索工作。你所需要做的是告訴`GridSearchCV`要試驗有哪些超參數，要試驗什么值，`GridSearchCV`就能用交叉驗證試驗所有可能超參數值的組合。例如，下面的代碼搜索了`RandomForestRegressor`超參數值的最佳組合： ```python from sklearn.model_selection import GridSearchCV param_grid = [ {'n_estimators': [3, 10, 30], 'max_features': [2, 4, 6, 8]}, {'bootstrap': [False], 'n_estimators': [3, 10], 'max_features': [2, 3, 4]}, ] forest_reg = RandomForestRegressor() grid_search = GridSearchCV(forest_reg, param_grid, cv=5, scoring='neg_mean_squared_error') grid_search.fit(housing_prepared, housing_labels) ``` > 當你不能確定超參數該有什么值，一個簡單的方法是嘗試連續的 10 的冪（如果想要一個粒度更小的搜尋，可以用更小的數，就像在這個例子中對超參數`n_estimators`做的）。 `param_grid`告訴 Scikit-Learn 首先評估所有的列在第一個`dict`中的`n_estimators`和`max_features`的`3 × 4 = 12`種組合（不用擔心這些超參數的含義，會在第 7 章中解釋）。然后嘗試第二個`dict`中超參數的`2 × 3 = 6`種組合，這次會將超參數`bootstrap`設為`False`而不是`True`（后者是該超參數的默認值）。 總之，網格搜索會探索`12 + 6 = 18`種`RandomForestRegressor`的超參數組合，會訓練每個模型五次（因為用的是五折交叉驗證）。換句話說，訓練總共有`18 × 5 = 90`輪！K 折將要花費大量時間，完成后，你就能獲得參數的最佳組合，如下所示： ```python >>> grid_search.best_params_ {'max_features': 6, 'n_estimators': 30} ``` > 提示：因為 30 是`n_estimators`的最大值，你也應該估計更高的值，因為評估的分數可能會隨`n_estimators`的增大而持續提升。 你還能直接得到最佳的估計器： ```python >>> grid_search.best_estimator_ RandomForestRegressor(bootstrap=True, criterion='mse', max_depth=None, max_features=6, max_leaf_nodes=None, min_samples_leaf=1, min_samples_split=2, min_weight_fraction_leaf=0.0, n_estimators=30, n_jobs=1, oob_score=False, random_state=None, verbose=0, warm_start=False) ``` > 注意：如果`GridSearchCV`是以（默認值）`refit=True`開始運行的，則一旦用交叉驗證找到了最佳的估計器，就會在整個訓練集上重新訓練。這是一個好方法，因為用更多數據訓練會提高性能。 當然，也可以得到評估得分： ```python >>> cvres = grid_search.cv_results_ ... for mean_score, params in zip(cvres["mean_test_score"], cvres["params"]): ... print(np.sqrt(-mean_score), params) ... 64912.0351358 {'max_features': 2, 'n_estimators': 3} 55535.2786524 {'max_features': 2, 'n_estimators': 10} 52940.2696165 {'max_features': 2, 'n_estimators': 30} 60384.0908354 {'max_features': 4, 'n_estimators': 3} 52709.9199934 {'max_features': 4, 'n_estimators': 10} 50503.5985321 {'max_features': 4, 'n_estimators': 30} 59058.1153485 {'max_features': 6, 'n_estimators': 3} 52172.0292957 {'max_features': 6, 'n_estimators': 10} 49958.9555932 {'max_features': 6, 'n_estimators': 30} 59122.260006 {'max_features': 8, 'n_estimators': 3} 52441.5896087 {'max_features': 8, 'n_estimators': 10} 50041.4899416 {'max_features': 8, 'n_estimators': 30} 62371.1221202 {'bootstrap': False, 'max_features': 2, 'n_estimators': 3} 54572.2557534 {'bootstrap': False, 'max_features': 2, 'n_estimators': 10} 59634.0533132 {'bootstrap': False, 'max_features': 3, 'n_estimators': 3} 52456.0883904 {'bootstrap': False, 'max_features': 3, 'n_estimators': 10} 58825.665239 {'bootstrap': False, 'max_features': 4, 'n_estimators': 3} 52012.9945396 {'bootstrap': False, 'max_features': 4, 'n_estimators': 10} ``` 在這個例子中，我們通過設定超參數`max_features`為 6，`n_estimators`為 30，得到了最佳方案。對這個組合，RMSE 的值是 49959，這比之前使用默認的超參數的值（52634）要稍微好一些。祝賀你，你成功地微調了最佳模型！ > 提示：不要忘記，你可以像超參數一樣處理數據準備的步驟。例如，網格搜索可以自動判斷是否添加一個你不確定的特征（比如，使用轉換器`CombinedAttributesAdder`的超參數`add_bedrooms_per_room`）。它還能用相似的方法來自動找到處理異常值、缺失特征、特征選擇等任務的最佳方法。 ### 隨機搜索 當探索相對較少的組合時，就像前面的例子，網格搜索還可以。但是當超參數的搜索空間很大時，最好使用`RandomizedSearchCV`。這個類的使用方法和類`GridSearchCV`很相似，但它不是嘗試所有可能的組合，而是通過選擇每個超參數的一個隨機值的特定數量的隨機組合。這個方法有兩個優點： + 如果你讓隨機搜索運行，比如 1000 次，它會探索每個超參數的 1000 個不同的值（而不是像網格搜索那樣，只搜索每個超參數的幾個值）。 + 你可以方便地通過設定搜索次數，控制超參數搜索的計算量。 ### 集成方法 另一種微調系統的方法是將表現最好的模型組合起來。組合（集成）之后的性能通常要比單獨的模型要好（就像隨機森林要比單獨的決策樹要好），特別是當單獨模型的誤差類型不同時。我們會在第 7 章更深入地講解這點。 ### 分析最佳模型和它們的誤差 通過分析最佳模型，常常可以獲得對問題更深的了解。比如，`RandomForestRegressor`可以指出每個屬性對于做出準確預測的相對重要性： ```python >>> feature_importances = grid_search.best_estimator_.feature_importances_ >>> feature_importances array([ 7.14156423e-02, 6.76139189e-02, 4.44260894e-02, 1.66308583e-02, 1.66076861e-02, 1.82402545e-02, 1.63458761e-02, 3.26497987e-01, 6.04365775e-02, 1.13055290e-01, 7.79324766e-02, 1.12166442e-02, 1.53344918e-01, 8.41308969e-05, 2.68483884e-03, 3.46681181e-03]) ``` 將重要性分數和屬性名放到一起： ```python >>> extra_attribs = ["rooms_per_hhold", "pop_per_hhold", "bedrooms_per_room"] >>> cat_one_hot_attribs = list(encoder.classes_) >>> attributes = num_attribs + extra_attribs + cat_one_hot_attribs >>> sorted(zip(feature_importances,attributes), reverse=True) [(0.32649798665134971, 'median_income'), (0.15334491760305854, 'INLAND'), (0.11305529021187399, 'pop_per_hhold'), (0.07793247662544775, 'bedrooms_per_room'), (0.071415642259275158, 'longitude'), (0.067613918945568688, 'latitude'), (0.060436577499703222, 'rooms_per_hhold'), (0.04442608939578685, 'housing_median_age'), (0.018240254462909437, 'population'), (0.01663085833886218, 'total_rooms'), (0.016607686091288865, 'total_bedrooms'), (0.016345876147580776, 'households'), (0.011216644219017424, '<1H OCEAN'), (0.0034668118081117387, 'NEAR OCEAN'), (0.0026848388432755429, 'NEAR BAY'), (8.4130896890070617e-05, 'ISLAND')] ``` 有了這個信息，你就可以丟棄一些不那么重要的特征（比如，顯然只要一個`ocean_proximity`的類型（INLAND）就夠了，所以可以丟棄掉其它的）。 你還應該看一下系統犯的誤差，搞清為什么會有些誤差，以及如何改正問題（添加更多的特征，或相反，去掉沒有什么信息的特征，清洗異常值等等）。 ### 用測試集評估系統 調節完系統之后，你終于有了一個性能足夠好的系統。現在就可以用測試集評估最后的模型了。這個過程沒有什么特殊的：從測試集得到預測值和標簽，運行`full_pipeline`轉換數據（調用`transform()`，而不是`fit_transform()`！），再用測試集評估最終模型： ```python final_model = grid_search.best_estimator_ X_test = strat_test_set.drop("median_house_value", axis=1) y_test = strat_test_set["median_house_value"].copy() X_test_prepared = full_pipeline.transform(X_test) final_predictions = final_model.predict(X_test_prepared) final_mse = mean_squared_error(y_test, final_predictions) final_rmse = np.sqrt(final_mse) # => evaluates to 48,209.6 ``` 評估結果通常要比交叉驗證的效果差一點，如果你之前做過很多超參數微調（因為你的系統在驗證集上微調，得到了不錯的性能，通常不會在未知的數據集上有同樣好的效果）。這個例子不屬于這種情況，但是當發生這種情況時，你一定要忍住不要調節超參數，使測試集的效果變好；這樣的提升不能推廣到新數據上。 然后就是項目的預上線階段：你需要展示你的方案（重點說明學到了什么、做了什么、沒做什么、做過什么假設、系統的限制是什么，等等），記錄下所有事情，用漂亮的圖表和容易記住的表達（比如，“收入中位數是房價最重要的預測量”）做一次精彩的展示。 ## 啟動、監控、維護系統 很好，你被允許啟動系統了！你需要為實際生產做好準備，特別是接入輸入數據源，并編寫測試。 你還需要編寫監控代碼，以固定間隔檢測系統的實時表現，當發生下降時觸發報警。這對于捕獲突然的系統崩潰和性能下降十分重要。做監控很常見，是因為模型會隨著數據的演化而性能下降，除非模型用新數據定期訓練。 評估系統的表現需要對預測值采樣并進行評估。這通常需要人來分析。分析者可能是領域專家，或者是眾包平臺（比如 Amazon Mechanical Turk 或 CrowdFlower）的工人。不管采用哪種方法，你都需要將人工評估的流水線植入系統。 你還要評估系統輸入數據的質量。有時因為低質量的信號（比如失靈的傳感器發送隨機值，或另一個團隊的輸出停滯），系統的表現會逐漸變差，但可能需要一段時間，系統的表現才能下降到一定程度，觸發警報。如果監測了系統的輸入，你就可能盡量早的發現問題。對于線上學習系統，監測輸入數據是非常重要的。 最后，你可能想定期用新數據訓練模型。你應該盡可能自動化這個過程。如果不這么做，非常有可能你需要每隔至少六個月更新模型，系統的表現就會產生嚴重波動。如果你的系統是一個線上學習系統，你需要定期保存系統狀態快照，好能方便地回滾到之前的工作狀態。 ## 實踐！ 希望這一章能告訴你機器學習項目是什么樣的，你能用學到的工具訓練一個好系統。你已經看到，大部分的工作是數據準備步驟、搭建監測工具、建立人為評估的流水線和自動化定期模型訓練，當然，最好能了解整個過程、熟悉三或四種算法，而不是在探索高級算法上浪費全部時間，導致在全局上的時間不夠。 因此，如果你還沒這樣做，現在最好拿起臺電腦，選擇一個感興趣的數據集，將整個流程從頭到尾完成一遍。一個不錯的著手開始的地點是競賽網站，比如 <http://kaggle.com/>：你會得到一個數據集，一個目標，以及分享經驗的人。 ## 練習 使用本章的房產數據集： 1. 嘗試一個支持向量機回歸器（`sklearn.svm.SVR`），使用多個超參數，比如`kernel="linear"`（多個超參數`C`值）。現在不用擔心這些超參數是什么含義。最佳的`SVR`預測表現如何？ 2. 嘗試用`RandomizedSearchCV`替換`GridSearchCV`。 3. 嘗試在準備流水線中添加一個只選擇最重要屬性的轉換器。 4. 嘗試創建一個單獨的可以完成數據準備和最終預測的流水線。 5. 使用`GridSearchCV`自動探索一些準備過程中的候選項。 練習題答案可以在[線上的 Jupyter notebook](https://github.com/ageron/handson-ml) 找到。