# 十五、使用 RNN 和 CNN 處理序列 > 譯者：[@SeanCheney](https://www.jianshu.com/u/130f76596b02) 擊球手擊出壘球，外場手會立即開始奔跑，并預測球的軌跡。外場手追蹤球，不斷調整移動步伐，最終在觀眾的掌聲中抓到它。無論是在聽完朋友的話還是早餐時預測咖啡的味道，你時刻在做的事就是在預測未來。在本章中，我們將討論循環神經網絡，一類可以預測未來的網絡（當然，是到某一點為止）。它們可以分析時間序列數據，比如股票價格，并告訴你什么時候買入和賣出。在自動駕駛系統中，他們可以預測行車軌跡，避免發生事故。更一般地說，它們可在任意長度的序列上工作，而不是截止目前我們討論的只能在固定長度的輸入上工作的網絡。舉個例子，它們可以將語句，文件，以及語音范本作為輸入，應用在在自動翻譯，語音到文本的自然語言處理應用中。 在本章中，我們將學習循環神經網絡的基本概念，如何使用時間反向傳播訓練網絡，然后用來預測時間序列。然后，會討論 RNN 面對的兩大難點： * 不穩定梯度（換句話說，在第 11 章中討論的梯度消失/爆炸），可以使用多種方法緩解，包括循環 dropout 和循環層歸一化。 * 有限的短期記憶，可以通過 LSTM 和 GRU 單元延長。 RNN 不是唯一能處理序列數據的神經網絡：對于小序列，常規緊密網絡也可以；對于長序列，比如音頻或文本，卷積神經網絡也可以。我們會討論這兩種方法，本章最后會實現一個 WaveNet：這是一種 CNN 架構，可以處理上萬個時間步的序列。在第 16 章，還會繼續學習 RNN，如何使用 RNN 來做自然語言處理，和基于注意力機制的新架構。 ## 循環神經元和層 到目前為止，我們主要關注的是前饋神經網絡，激活僅從輸入層到輸出層的一個方向流動（附錄 E 中的幾個網絡除外）。 循環神經網絡看起來非常像一個前饋神經網絡，除了它也有連接指向后方。 讓我們看一下最簡單的 RNN，由一個神經元接收輸入，產生一個輸出，并將輸出發送回自己，如圖 15-1（左）所示。 在每個時間步`t`（也稱為一個幀），這個循環神經元接收輸入 x_(t)以及它自己的前一時間步長 y_(t-1) 的輸出。 因為第一個時間步驟沒有上一次的輸出，所以是 0。可以用時間軸來表示這個微小的網絡，如圖 15-1（右）所示。 這被稱為隨時間展開網絡。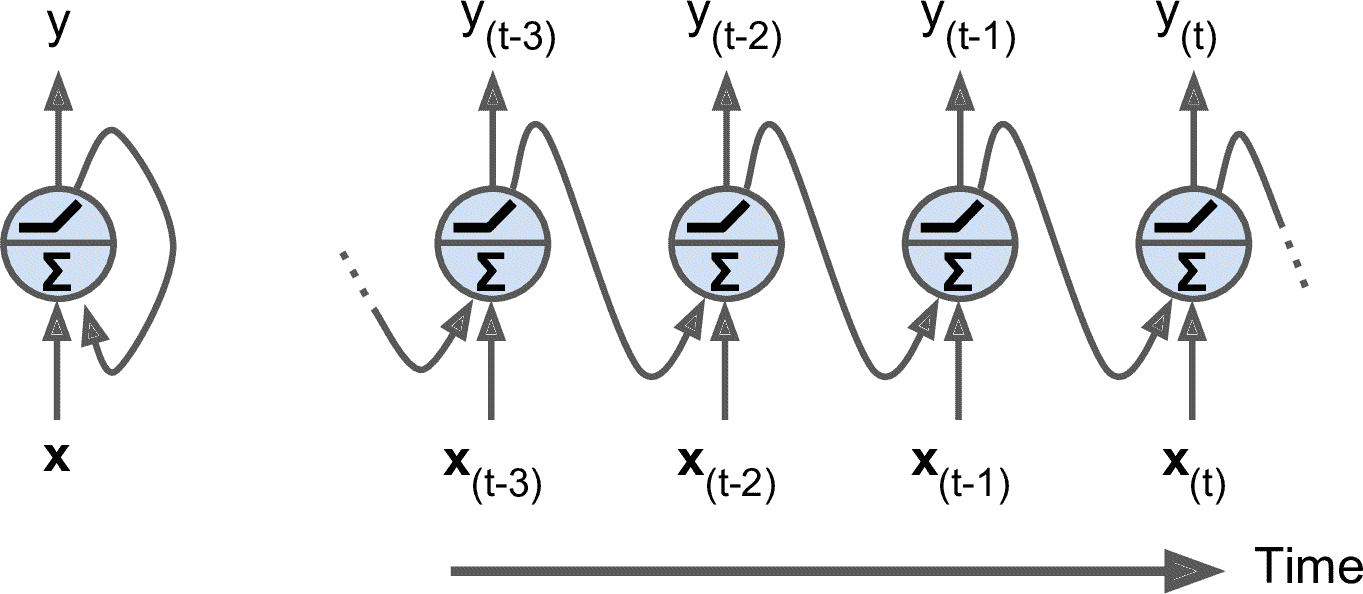 圖 15-1 循環神經網絡（左），隨時間展開網絡（右） 你可以輕松創建一個循環神經元層。 在每個時間步 t，每個神經元都接收輸入矢量 x_(t) 和前一個時間步 y_(t-1) 的輸出矢量，如圖 15-2 所示。 注意，輸入和輸出都是矢量（當只有一個神經元時，輸出是一個標量）。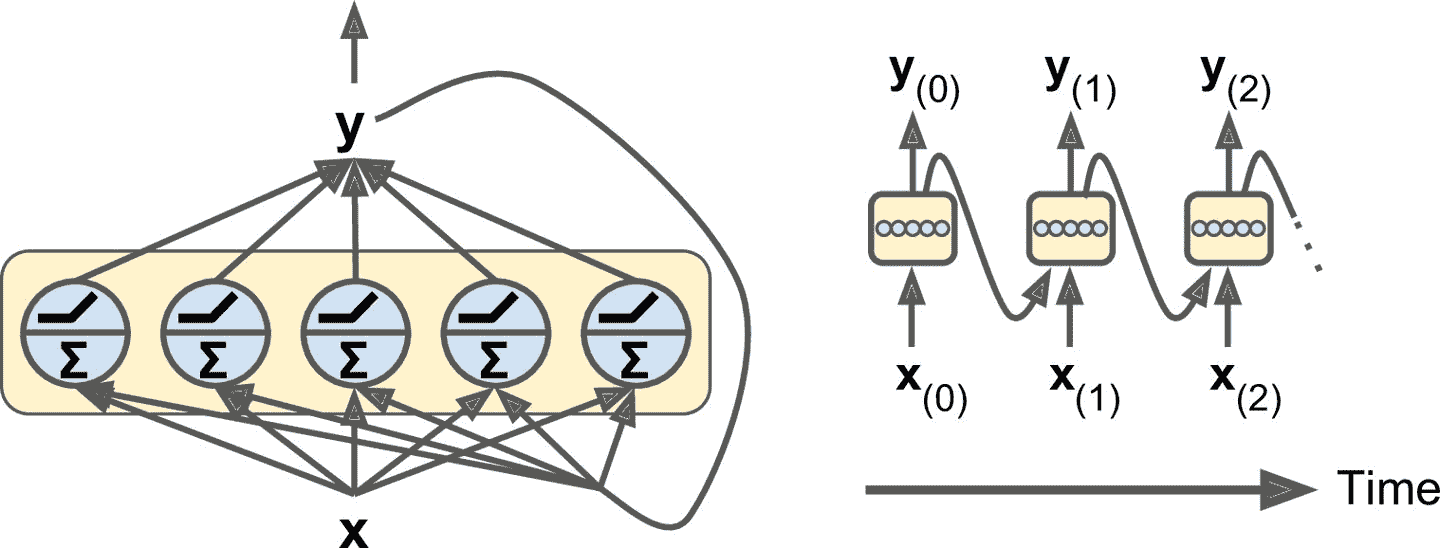 圖 15-2 一層循環神經元（左），及其隨時間展開（右） 每個循環神經元有兩組權重：一組用于輸入 x_(t)，另一組用于前一時間步長 y_(t-1) 的輸出。 我們稱這些權重向量為 w_x 和 w_y。如果考慮的是整個循環神經元層，可以將所有權重矢量放到兩個權重矩陣中，W_x 和 W_y。整個循環神經元層的輸出可以用公式 15-1 表示（`b`是偏差項，`φ(·)`是激活函數，例如 ReLU）。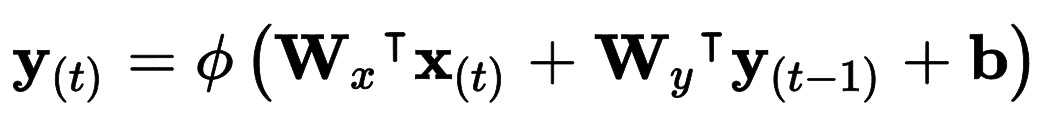 公式 15-1 單個實例的循環神經元層的輸出 就像前饋神經網絡一樣，可以將所有輸入和時間步`t`放到輸入矩陣 X_(t)中，一次計算出整個小批次的輸出：（見公式 15-2）。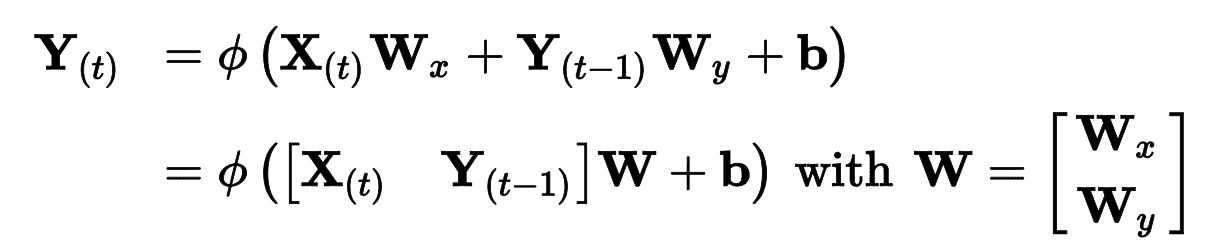 公式 15-2 小批次實例的循環層輸出 在這個公式中： * Y_(t) 是 m × n_neurons 矩陣，包含在小批次中每個實例在時間步`t`的層輸出（`m`是小批次中的實例數，n_neurons 是神經元數）。 * X_(t) 是 m × n_inputs 矩陣，包含所有實例的輸入 （n_inputs 是輸入特征的數量）。 * W_x 是 n_inputs × n_neurons 矩陣，包含當前時間步的輸入的連接權重。 * W_y 是 n_neurons × n_neurons 矩陣，包含上一個時間步的輸出的連接權重。 * `b`是大小為 n_neurons 的矢量，包含每個神經元的偏置項。 * 權重矩陣 W_x 和 W_y 通常縱向連接成一個權重矩陣`W`，形狀為(n_inputs + n_neurons) × n_neurons（見公式 15-2 的第二行） 注意，Y_(t) 是 X_(t) 和 Y_(t-1) 的函數，Y_(t-1)是 X_(t-1)和 Y_(t-2) 的函數，以此類推。這使得 Y_(t) 是從時間`t = 0`開始的所有輸入（即 X₍₀₎，X₍₁₎，...，X_(t)）的函數。 在第一個時間步，`t = 0`，沒有以前的輸出，所以它們通常被假定為全零。 ### 記憶單元 由于時間`t`的循環神經元的輸出，是由所有先前時間步驟計算出來的的函數，你可以說它有一種記憶形式。神經網絡的一部分，保留一些跨越時間步長的狀態，稱為存儲單元（或簡稱為單元）。單個循環神經元或循環神經元層是非常基本的單元，只能學習短期規律（取決于具體任務，通常是 10 個時間步）。本章后面我們將介紹一些更為復雜和強大的單元，可以學習更長時間步的規律（也取決于具體任務，大概是 100 個時間步）。 一般情況下，時間步`t`的單元狀態，記為 h_(t)（`h`代表“隱藏”），是該時間步的某些輸入和前一時間步狀態的函數：h_(t) = f(h_(t–1), x_(t))。 其在時間步`t`的輸出，表示為 y_(t)，也和前一狀態和當前輸入的函數有關。 我們已經討論過的基本單元，輸出等于單元狀態，但是在更復雜的單元中并不總是如此，如圖 15-3 所示。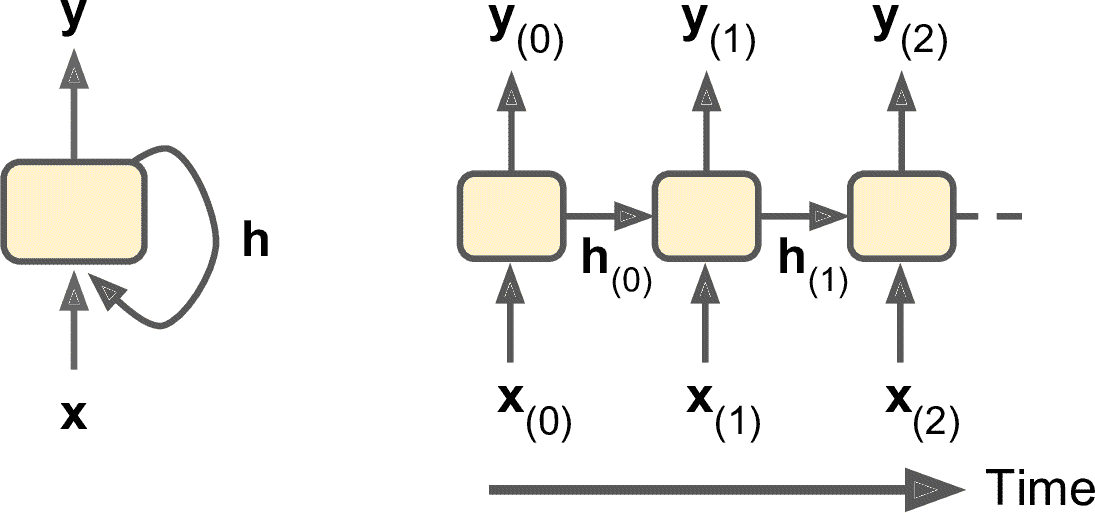 圖 15-3 單元的隱藏狀態和輸出可能不同 ## 輸入和輸出序列 RNN 可以同時輸入序列并輸出序列（見圖 15-4，左上角的網絡）。這種序列到序列的網絡可以有效預測時間序列（如股票價格）：輸入過去`N`天價格，則輸出向未來移動一天的價格（即，從`N - 1`天前到明天）。 或者，你可以向網絡輸入一個序列，忽略除最后一項之外的所有輸出（圖 15-4 右上角的網絡）。 換句話說，這是一個序列到矢量的網絡。 例如，你可以向網絡輸入與電影評論相對應的單詞序列，網絡輸出情感評分（例如，從`-1 [討厭]`到`+1 [喜歡]`）。 相反，可以向網絡一遍又一遍輸入相同的矢量（見圖 15-4 的左下角），輸出一個序列。這是一個矢量到序列的網絡。 例如，輸入可以是圖像（或是 CNN 的結果），輸出是該圖像的標題。 最后，可以有一個序列到矢量的網絡，稱為編碼器，后面跟著一個稱為解碼器的矢量到序列的網絡（見圖 15-4 右下角）。 例如，這可以用于將句子從一種語言翻譯成另一種語言。 給網絡輸入一種語言的一句話，編碼器會把這個句子轉換成單一的矢量表征，然后解碼器將這個矢量解碼成另一種語言的句子。 這種稱為編碼器 - 解碼器的兩步模型，比用單個序列到序列的 RNN 實時地進行翻譯要好得多，因為句子的最后一個單詞可以影響翻譯的第一句話，所以你需要等到聽完整個句子才能翻譯。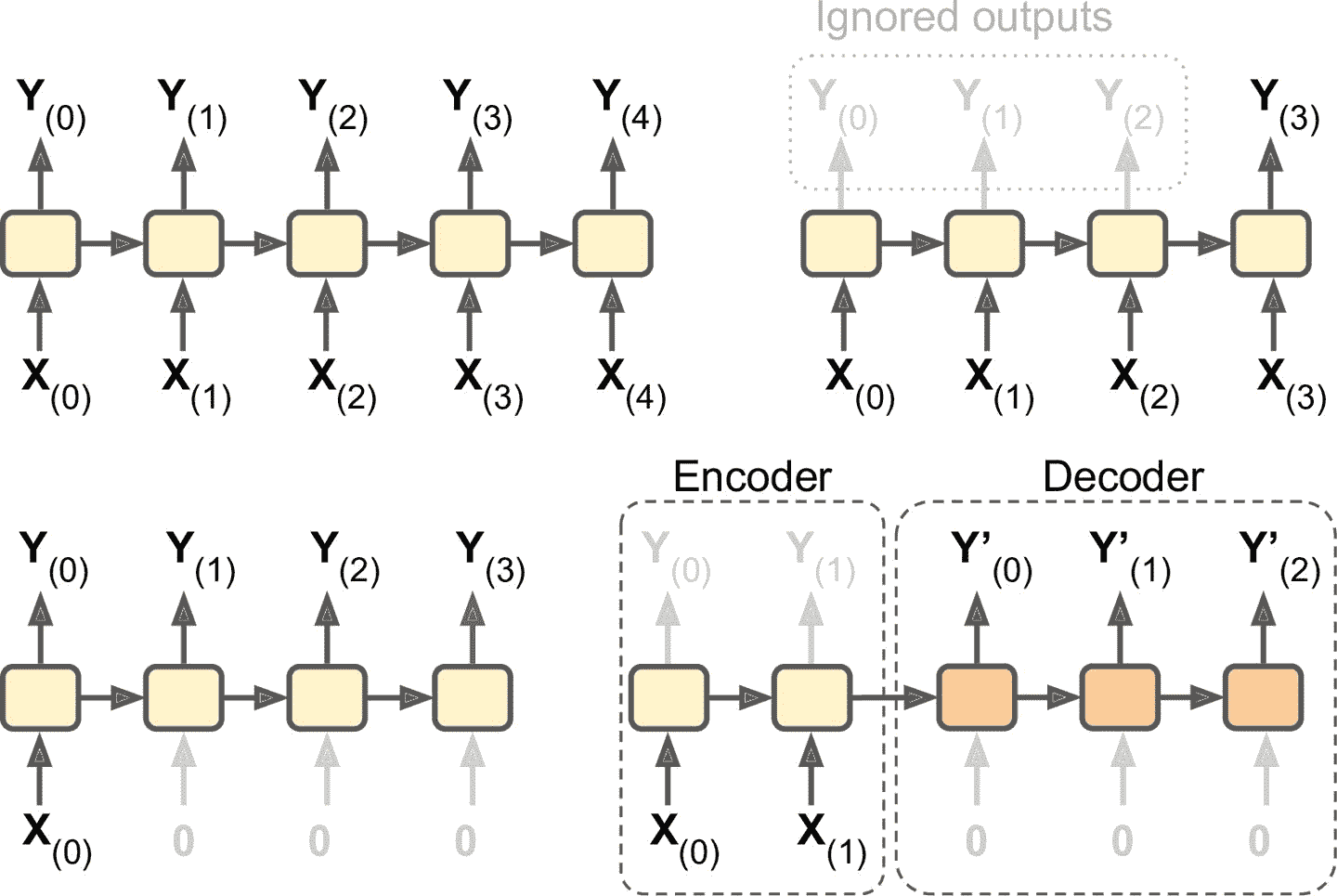第 16 章還會介紹如何實現編碼器-解碼器（會比圖 15-4 中復雜） 圖 15-4 序列到序列（左上），序列到矢量（右上），矢量到序列（左下），延遲序列到序列（右下） ## 訓練 RNN 訓練 RNN 訣竅是在時間上展開（就像我們剛剛做的那樣），然后只要使用常規反向傳播（見圖 15-5）。 這個策略被稱為時間上的反向傳播（BPTT）。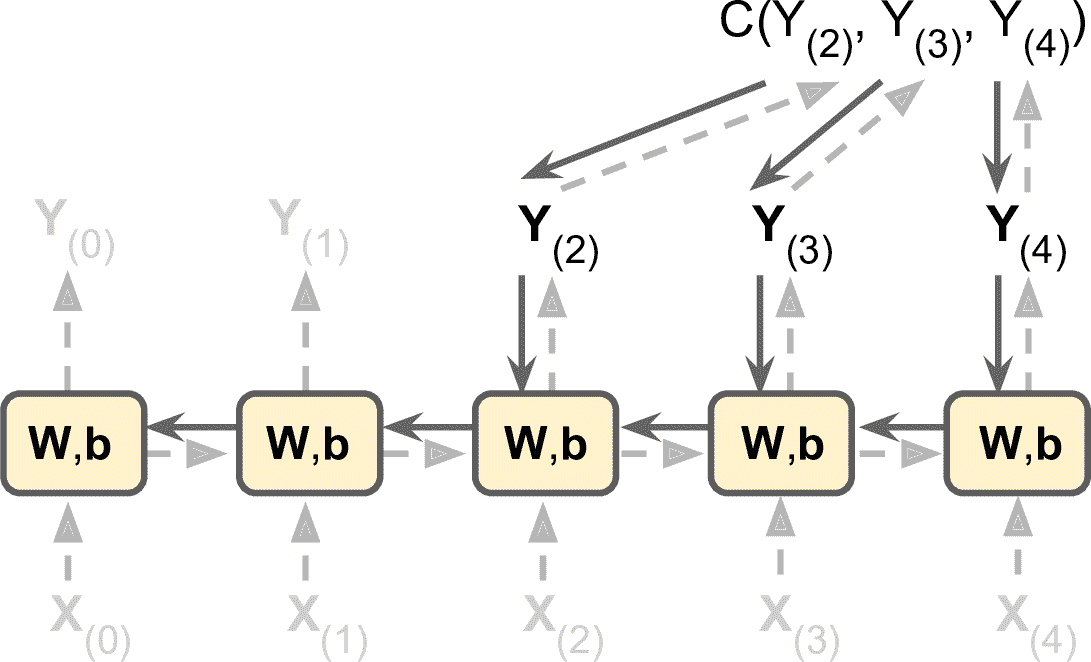 圖 15-5 隨時間反向傳播 就像在正常的反向傳播中一樣，展開的網絡（用虛線箭頭表示）中先有一個正向傳播（虛線）。然后使用損失函數 C(Y₍₀₎, Y₍₁₎, …Y_(T)) 評估輸出序列（其中 T 是最大時間步）。這個損失函數會忽略一些輸出，見圖 15-5（例如，在序列到矢量的 RNN 中，除了最后一項，其它的都被忽略了）。損失函數的梯度通過展開的網絡反向傳播（實線箭頭）。最后使用在 BPTT 期間計算的梯度來更新模型參數。注意，梯度在損失函數所使用的所有輸出中反向流動，而不僅僅通過最終輸出（例如，在圖 15-5 中，損失函數使用網絡的最后三個輸出 Y₍₂₎，Y₍₃₎ 和 Y₍₄₎，所以梯度流經這三個輸出，但不通過 Y₍₀₎ 和 Y₍₁₎。而且，由于在每個時間步驟使用相同的參數`W`和`b`，所以反向傳播將做正確的事情并對所有時間步求和。 幸好，tf.keras 處理了這些麻煩。 ## 預測時間序列 假設你在研究網站每小時的活躍用戶數，或是所在城市的每日氣溫，或公司的財務狀況，用多種指標做季度衡量。在這些任務中，數據都是一個序列，每步有一個或多個值。這被稱為時間序列。在前兩個任務中，每個時間步只有一個值，它們是單變量時間序列。在財務狀況的任務中，每個時間步有多個值（利潤、欠賬，等等），所以是多變量時間序列。典型的任務是預測未來值，稱為“預測”。另一個任務是填空：預測（或“后測”）過去的缺失值，這被稱為“填充”。例如，圖 15-6 展示了 3 個單變量時間序列，每個都有 50 個時間步，目標是預測下一個時間步的值（用 X 表示）。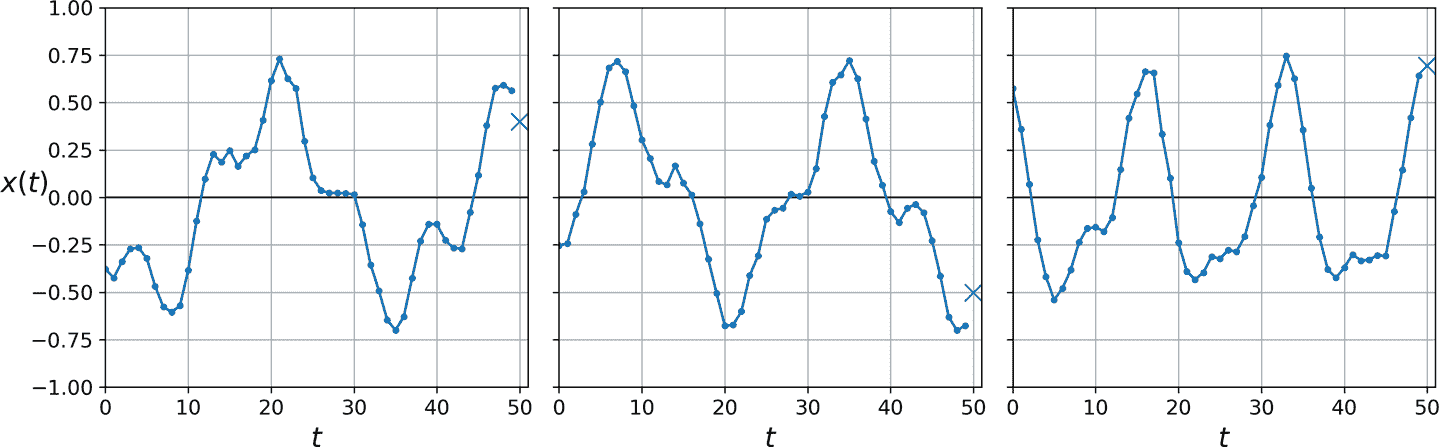 圖 15-6 時間序列預測 簡單起見，使用函數`generate_time_series()`生成的時間序列，如下： ```py def generate_time_series(batch_size, n_steps): freq1, freq2, offsets1, offsets2 = np.random.rand(4, batch_size, 1) time = np.linspace(0, 1, n_steps) series = 0.5 * np.sin((time - offsets1) * (freq1 * 10 + 10)) # wave 1 series += 0.2 * np.sin((time - offsets2) * (freq2 * 20 + 20)) # + wave 2 series += 0.1 * (np.random.rand(batch_size, n_steps) - 0.5) # + noise return series[..., np.newaxis].astype(np.float32) ``` 這個函數可以根據要求創建出時間序列（通過`batch_size`參數），長度為`n_steps`，每個時間步只有 1 個值。函數返回 NumPy 數組，形狀是[批次大小, 時間步數, 1]，每個序列是兩個正弦波之和（固定強度+隨機頻率和相位），加一點噪音。 > 筆記：當處理時間序列時（和其它類型的時間序列），輸入特征通常用 3D 數組來表示，其形狀是 [批次大小, 時間步數, 維度]，對于單變量時間序列，其維度是 1，多變量時間序列的維度是其維度數。 用這個函數來創建訓練集、驗證集和測試集： ```py n_steps = 50 series = generate_time_series(10000, n_steps + 1) X_train, y_train = series[:7000, :n_steps], series[:7000, -1] X_valid, y_valid = series[7000:9000, :n_steps], series[7000:9000, -1] X_test, y_test = series[9000:, :n_steps], series[9000:, -1] ``` `X_train`包含 7000 個時間序列（即，形狀是[7000, 50, 1]），`X_valid`有 2000 個，`X_test`有 1000 個。因為預測的是單一值，目標值是列矢量（`y_train`的形狀是[7000, 1]）。 ### 基線模型 使用 RNN 之前，最好有基線指標，否則做出來的模型可能比基線模型還糟。例如，最簡單的方法，是預測每個序列的最后一個值。這個方法被稱為樸素預測，有時很難被超越。在這個例子中，它的均方誤差為 0.020： ```py >>> y_pred = X_valid[:, -1] >>> np.mean(keras.losses.mean_squared_error(y_valid, y_pred)) 0.020211367 ``` 另一個簡單的方法是使用全連接網絡。因為結果要是打平的特征列表，需要加一個`Flatten`層。使用簡單線性回歸模型，使預測值是時間序列中每個值的線性組合： ```py model = keras.models.Sequential([ keras.layers.Flatten(input_shape=[50, 1]), keras.layers.Dense(1) ]) ``` 使用 MSE 損失、Adam 優化器編譯模型，在訓練集上訓練 20 個周期，用驗證集評估，最終得到的 MSE 值為 0.004。比樸素預測強多了！ ### 實現一個簡單 RNN 搭建一個簡單 RNN 模型： ```py model = keras.models.Sequential([ keras.layers.SimpleRNN(1, input_shape=[None, 1]) ]) ``` 這是能實現的最簡單的 RNN。只有 1 個層，1 個神經元，如圖 15-1。不用指定輸入序列的長度（和之前的模型不同），因為循環神經網絡可以處理任意的時間步（這就是為什么將第一個輸入維度設為`None`）。默認時，`SimpleRNN`使用雙曲正切激活函數。和之前看到的一樣：初始狀態 h_(init)設為 0，和時間序列的第一個值 x₍₀₎一起傳遞給神經元。神經元計算這兩個值的加權和，對結果使用雙曲正切激活函數，得到第一個輸出 y₍₀₎。在簡單 RNN 中，這個輸出也是新狀態 h₍₀₎。這個新狀態和下一個輸入值 x₍₁₎，按照這個流程，直到輸出最后一個值，y₄₉。所有這些都是同時對每個時間序列進行的。 > 筆記：默認時，Keras 的循環層只返回最后一個輸出。要讓其返回每個時間步的輸出，必須設置`return_sequences=True`。 用這個模型編譯、訓練、評估（和之前一樣，用 Adam 訓練 20 個周期），你會發現它的 MSE 只有 0.014。擊敗了樸素預測，但不如簡單線性模型。對于每個神經元，線性簡單模型中每個時間步驟每個輸入就有一個參數（前面用過的簡單線性模型一共有 51 個參數）。相反，對于簡單 RNN 中每個循環神經元，每個輸入每個隱藏狀態只有一個參數（在簡單 RNN 中，就是每層循環神經元的數量），加上一個偏置項。在這個簡單 RNN 中，只有三個參數。 > 趨勢和季節性 > > 還有其它預測時間序列的模型，比如權重移動平均模型或自動回歸集成移動平均（ARIMA）模型。某些模型需要先移出趨勢和季節性。例如，如果要研究網站的活躍用戶數，它每月會增長 10%，就需要去掉這個趨勢。訓練好模型之后，在做預測時，你可以將趨勢加回來做最終的預測。相似的，如果要預測防曬霜的每月銷量，會觀察到明顯的季節性：每年夏天賣的多。需要將季節性從時間序列去除，比如計算每個時間步和前一年的差值（這個方法被稱為差分）。然后，當訓練好模型，做預測時，可以將季節性加回來，來得到最終結果。 > > 使用 RNN 時，一般不需要做這些，但在有些任務中可以提高性能，因為模型不是非要學習這些趨勢或季節性。 很顯然，這個簡單 RNN 過于簡單了，性能不成。下面就來添加更多的循環層！ ### 深度 RNN 將多個神經元的層堆起來，見圖 15-7。就形成了深度 RNN。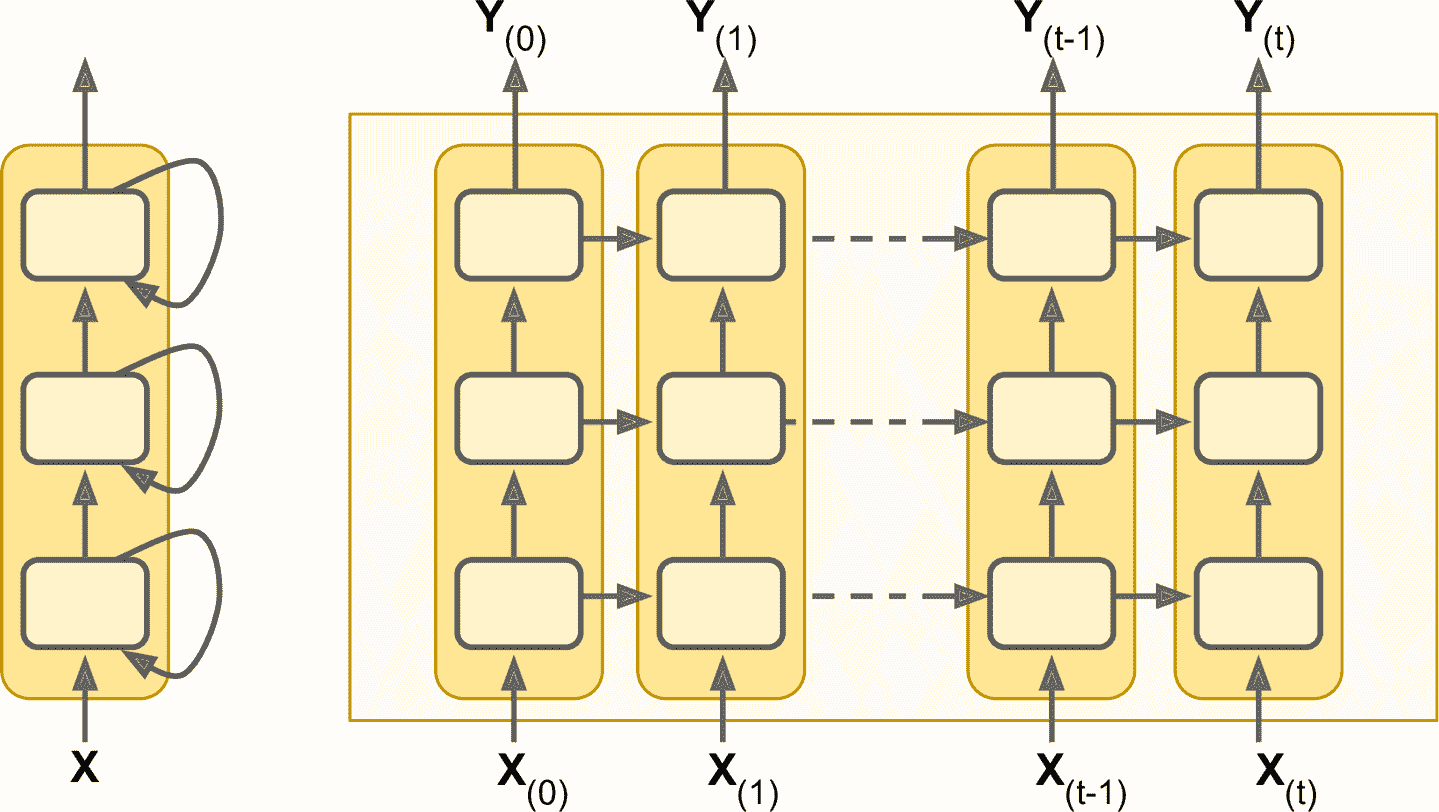 圖 15-7 深度 RNN（左）和隨時間展開的深度 RNN（右） 用 tf.keras 實現深度 RNN 相當容易：將循環層堆起來就成。在這個例子中，我們使用三個`SimpleRNN`層（也可以添加其它類型的循環層，比如 LSTM 或 GRU）： ```py model = keras.models.Sequential([ keras.layers.SimpleRNN(20, return_sequences=True, input_shape=[None, 1]), keras.layers.SimpleRNN(20, return_sequences=True), keras.layers.SimpleRNN(1) ]) ``` > 警告：所有循環層一定要設置`return_sequences=True`（除了最后一層，因為最后一層只關心輸出）。如果沒有設置，輸出的是 2D 數組（只有最終時間步的輸出），而不是 3D 數組（包含所有時間步的輸出），下一個循環層就接收不到 3D 格式的序列數據。 如果對這個模型做編譯，訓練和評估，其 MSE 值可以達到 0.003。總算打敗了線性模型！ 最后一層不夠理想：因為要預測單一值，每個時間步只能有一個輸出值，最終層只能有一個神經元。但是一個神經元意味著隱藏態只有一個值。RNN 大部分使用其他循環層的隱藏態的所有信息，最后一層的隱藏態不怎么用到。另外，因為`SimpleRNN`層默認使用 tanh 激活函數，預測值位于-1 和 1 之間。想使用另一個激活函數該怎么辦呢？出于這些原因，最好使用緊密層：運行更快，準確率差不多，可以選擇任何激活函數。如果做了替換，要將第二個循環層的`return_sequences=True`刪掉： ```py model = keras.models.Sequential([ keras.layers.SimpleRNN(20, return_sequences=True, input_shape=[None, 1]), keras.layers.SimpleRNN(20), keras.layers.Dense(1) ]) ``` 如果訓練這個模型，會發現它收斂更快，效果也不錯。 ### 提前預測幾個時間步 目前為止我們只是預測下一個時間步的值，但也可以輕易地提前預測幾步，只要改變目標就成（例如，要提前預測 10 步，只要將目標變為 10 步就成）。但如果想預測后面的 10 個值呢？ 第一種方法是使用訓練好的模型，預測出下一個值，然后將這個值添加到輸入中（假設這個預測值真實發生了），使用這個模型再次預測下一個值，依次類推，見如下代碼： ```py series = generate_time_series(1, n_steps + 10) X_new, Y_new = series[:, :n_steps], series[:, n_steps:] X = X_new for step_ahead in range(10): y_pred_one = model.predict(X[:, step_ahead:])[:, np.newaxis, :] X = np.concatenate([X, y_pred_one], axis=1) Y_pred = X[:, n_steps:] ``` 想象的到，第一個預測值比后面的更準，因為錯誤可能會累積（見圖 15-8）。如果在驗證集上評估這個方法，MSE 值為 0.029。MSE 比之前高多了，但因為任務本身難，這個對比意義不大。將其余樸素預測（預測時間序列可以恒定 10 個步驟）或簡單線性模型對比的意義更大。樸素方法效果很差（MSE 值為 0.223），線性簡單模型的 MSE 值為 0.0188：比 RNN 的預測效果好，并且還快。如果只想在復雜任務上提前預測幾步的話，這個方法就夠了。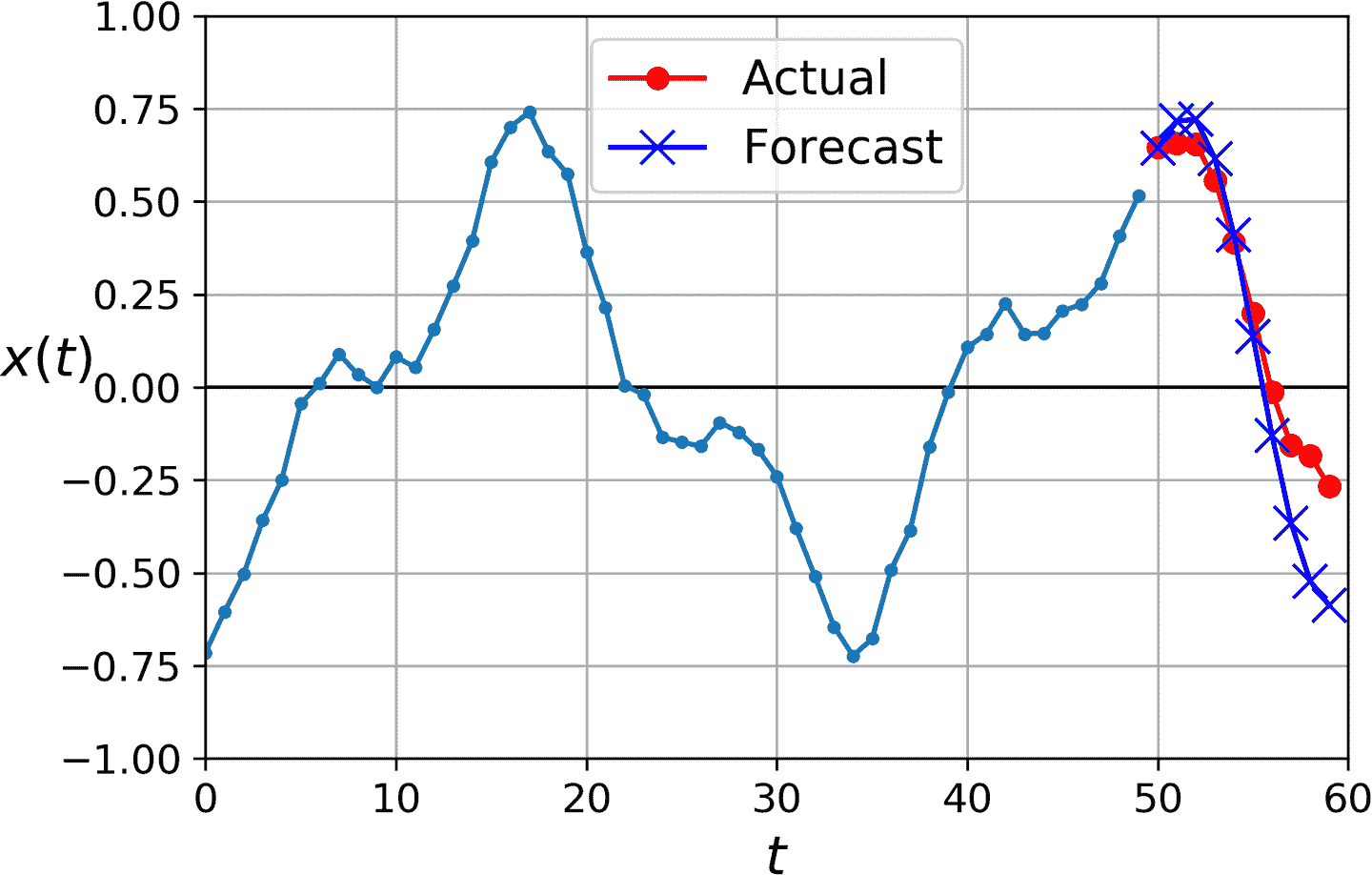 圖 15-8 提前預測 10 步，每次 1 步 第二種方法是訓練一個 RNN，一次性預測出 10 個值。還可以使用序列到矢量模型，但輸出的是 10 個值。但是，我們先需要修改矢量，時期含有 10 個值： ```py series = generate_time_series(10000, n_steps + 10) X_train, Y_train = series[:7000, :n_steps], series[:7000, -10:, 0] X_valid, Y_valid = series[7000:9000, :n_steps], series[7000:9000, -10:, 0] X_test, Y_test = series[9000:, :n_steps], series[9000:, -10:, 0] ``` 然后使輸出層有 10 個神經元： ```py model = keras.models.Sequential([ keras.layers.SimpleRNN(20, return_sequences=True, input_shape=[None, 1]), keras.layers.SimpleRNN(20), keras.layers.Dense(10) ]) ``` 訓練好這個模型之后，就可以一次預測出后面的 10 個值了： ```py Y_pred = model.predict(X_new) ``` 這個模型的效果不錯：預測 10 個值的 MSE 值為 0.008。比線性模型強多了。但還有繼續改善的空間，除了在最后的時間步用訓練模型預測接下來的 10 個值，還可以在每個時間步預測接下來的 10 個值。換句話說，可以將這個序列到矢量的 RNN 變成序列到序列的 RNN。這種方法的優勢，是損失會包含 RNN 的每個時間步的輸出項，不僅是最后時間步的輸出。這意味著模型中會流動著更多的誤差梯度，梯度不必只通過時間流動；還可以從輸出流動。這樣可以穩定和加速訓練。 更加清楚一點，在時間步 0，模型輸出一個包含時間步 1 到 10 的預測矢量，在時間步 1，模型輸出一個包含時間步 2 到 11 的預測矢量，以此類推。因此每個目標必須是一個序列，其長度和輸入序列長度相同，每個時間步包含一個 10 維矢量。先準備目標序列： ```py Y = np.empty((10000, n_steps, 10)) # each target is a sequence of 10D vectors for step_ahead in range(1, 10 + 1): Y[:, :, step_ahead - 1] = series[:, step_ahead:step_ahead + n_steps, 0] Y_train = Y[:7000] Y_valid = Y[7000:9000] Y_test = Y[9000:] ``` > 筆記：目標要包含出現在輸入中的值（`X_train` 和 `Y_train`有許多重復），聽起來很奇怪。這不是作弊嗎？其實不是：在每個時間步，模型只知道過去的時間步，不能向前看。這個模型被稱為因果模型。 要將模型變成序列到序列的模型，必須給所有循環層（包括最后一個）設置`return_sequences=True`，還必須在每個時間步添加緊密輸出層。出于這個目的，Keras 提供了`TimeDistributed`層：它將任意層（比如，緊密層）包裝起來，然后在輸入序列的每個時間步上使用。通過變形輸入，將每個時間步處理為獨立實例（即，將輸入從 [批次大小, 時間步數, 輸入維度] 變形為 [批次大小 × 時間步數, 輸入維度] ；在這個例子中，因為前一`SimpleRNN`有 20 個神經元，輸入的維度數是 20），這個層的效率很高。然后運行緊密層，最后將輸出變形為序列（即，將輸出從 [批次大小 × 時間步數, 輸出維度] 變形為 [批次大小, 時間步數, 輸出維度] ；在這個例子中，輸出維度數是 10，因為緊密層有 10 個神經元）。下面是更新后的模型： ```py model = keras.models.Sequential([ keras.layers.SimpleRNN(20, return_sequences=True, input_shape=[None, 1]), keras.layers.SimpleRNN(20, return_sequences=True), keras.layers.TimeDistributed(keras.layers.Dense(10)) ]) ``` 緊密層實際上是支持序列（和更高維度的輸入）作為輸入的：如同`TimeDistributed(Dense(…))`一樣處理序列，意味著只應用在最后的輸入維度上（所有時間步獨立）。因此，因此可以將最后一層替換為`Dense(10)`。但為了能夠清晰，我們還是使用`TimeDistributed(Dense(10))`，因為清楚的展示了緊密層獨立應用在了每個時間上，并且模型會輸出一個序列，不僅僅是一個單矢量。 訓練時需要所有輸出，但預測和評估時，只需最后時間步的輸出。因此盡管訓練時依賴所有輸出的 MSE，評估需要一個自定義指標，只計算最后一個時間步輸出值的 MSE： ```py def last_time_step_mse(Y_true, Y_pred): return keras.metrics.mean_squared_error(Y_true[:, -1], Y_pred[:, -1]) optimizer = keras.optimizers.Adam(lr=0.01) model.compile(loss="mse", optimizer=optimizer, metrics=[last_time_step_mse]) ``` 得到的 MSE 值為 0.006，比前面的模型提高了 25%。可以將這個方法和第一個結合起來：先用這個 RNN 預測接下來的 10 個值，然后將結果和輸入序列連起來，再用模型預測接下來的 10 個值，以此類推。使用這個方法，可以預測任意長度的序列。對長期預測可能不那么準確，但用來生成音樂和文字是足夠的，第 16 章有例子。 > 提示：當預測時間序列時，最好給預測加上誤差條。要這么做，一個高效的方法是用 MC Dropout，第 11 章介紹過：給每個記憶單元添加一個 MC Dropout 層丟失部分輸入和隱藏狀態。訓練之后，要預測新的時間序列，可以多次使用模型計算每一步預測值的平均值和標準差。 簡單 RNN 在預測時間序列或處理其它類型序列時表現很好，但在長序列上表現不佳。接下來就探究其原因和解決方法。 ## 處理長序列 在訓練長序列的 RNN 模型時，必須運行許多時間步，展開的 RNN 變成了一個很深的網絡。正如任何深度神經網絡一樣，它面臨不穩定梯度問題（第 11 章討論過），使訓練無法停止，或訓練不穩定。另外，當 RNN 處理長序列時，RNN 會逐漸忘掉序列的第一個輸入。下面就來看看這兩個問題，先是第一個問題。 ### 應對不穩定梯度 很多之前討論過的緩解不穩定梯度的技巧都可以應用在 RNN 中：好的參數初始化方式，更快的優化器，dropout，等等。但是非飽和激活函數（如 ReLU）的幫助不大；事實上，它會導致 RNN 更加不穩定。為什么呢？假設梯度下降更新了權重，可以令第一個時間步的輸出提高。因為每個時間步使用的權重相同，第二個時間步的輸出也會提高，這樣就會導致輸出爆炸 —— 不飽和激活函數不能阻止這個問題。要降低爆炸風險，可以使用更小的學習率，更簡單的方法是使用一個飽和激活函數，比如雙曲正切函數（這就解釋了為什么 tanh 是默認選項）。同樣的道理，梯度本身也可能爆炸。如果觀察到訓練不穩定，可以監督梯度的大小（例如，使用 TensorBoard），看情況使用梯度裁剪。 另外，批歸一化也沒什么幫助。事實上，不能在時間步驟之間使用批歸一化，只能在循環層之間使用。更加準確點，技術上可以將 BN 層添加到記憶單元上（后面會看到），這樣就可以應用在每個時間步上了（既對輸入使用，也對前一步的隱藏態使用）。但是，每個時間步用 BN 層相同，參數也相同，與輸入和隱藏態的大小和偏移無關。在實踐中，César Laurent 等人在 2015 年的[一篇論文](https://links.jianshu.com/go?to=https%3A%2F%2Fhoml.info%2Frnnbn)展示，這么做的效果不好：作者發現 BN 層只對輸入有用，而對隱藏態沒用。換句話說，在循環層之間使用 BN 層時，效果只有一點（即在圖 15-7 中垂直使用），在循環層之內使用，效果不大（即，水平使用）。在 Keras 中，可以在每個循環層之前添加`BatchNormalization`層，但不要期待太高。 另一種歸一化的形式效果好些：層歸一化。它是由 Jimmy Lei Ba 等人在 2016 年的[一篇論文](https://links.jianshu.com/go?to=https%3A%2F%2Fhoml.info%2Flayernorm)中提出的：它跟批歸一化很像，但不是在批次維度上做歸一化，而是在特征維度上歸一化。這么做的一個優勢是可以獨立對每個實例，實時計算所需的統計量。這還意味著訓練和測試中的行為是一致的（這點和 BN 相反），且不需要使用指數移動平均來估計訓練集中所有實例的特征統計。和 BN 一樣，層歸一化會學習每個輸入的比例和偏移參數。在 RNN 中，層歸一化通常用在輸入和隱藏態的線型組合之后。 使用 tf.keras 在一個簡單記憶單元中實現層歸一化。要這么做，需要定義一個自定義記憶單元。就像一個常規層一樣，`call()`接收兩個參數：當前時間步的`inputs`和上一時間步的隱藏`states`。`states`是一個包含一個或多個張量的列表。在簡單 RNN 單元中，`states`包含一個等于上一時間步輸出的張量，但其它單元可能包含多個狀態張量（比如`LSTMCell`有長期狀態和短期狀態）。單元還必須有一個`state_size`屬性和一個`output_size`屬性。在簡單 RNN 中，這兩個屬性等于神經元的數量。下面的代碼實現了一個自定義記憶單元，作用類似于`SimpleRNNCell`，但會在每個時間步做層歸一化： ```py class LNSimpleRNNCell(keras.layers.Layer): def __init__(self, units, activation="tanh", **kwargs): super().__init__(**kwargs) self.state_size = units self.output_size = units self.simple_rnn_cell = keras.layers.SimpleRNNCell(units, activation=None) self.layer_norm = keras.layers.LayerNormalization() self.activation = keras.activations.get(activation) def call(self, inputs, states): outputs, new_states = self.simple_rnn_cell(inputs, states) norm_outputs = self.activation(self.layer_norm(outputs)) return norm_outputs, [norm_outputs] ``` 代碼不難。和其它自定義類一樣，`LNSimpleRNNCell`繼承自`keras.layers.Layer`。構造器接收 unit 的數量、激活函數、設置`state_size` 和`output_size`屬性，創建一個沒有激活函數的`SimpleRNNCell`（因為要在線性運算之后、激活函數之前運行層歸一化）。然后構造器創建`LayerNormalization`層，最終拿到激活函數。`call()`方法先應用簡單 RNN 單元，計算當前輸入和上一隱藏態的線性組合，然后返回結果兩次（事實上，在`SimpleRNNCell`中，輸入等于隱藏狀態：換句話說，`new_states[0]`等于`outputs`，因此可以放心地在剩下的`call()`中忽略`new_states`）。然后，`call()`應用層歸一化，然后使用激活函數。最后，返回去輸出兩次（一次作為輸出，一次作為新的隱藏態）。要使用這個自定義單元，需要做的是創建一個`keras.layers.RNN`層，傳給其單元實例： ```py model = keras.models.Sequential([ keras.layers.RNN(LNSimpleRNNCell(20), return_sequences=True, input_shape=[None, 1]), keras.layers.RNN(LNSimpleRNNCell(20), return_sequences=True), keras.layers.TimeDistributed(keras.layers.Dense(10)) ]) ``` 相似地，可以創建一個自定義單元，在時間步之間應用 dropout。但有一個更簡單的方法：Keras 提供的所有循環層（除了`keras.layers.RNN`）和單元都有一個`dropout`超參數和一個`recurrent_dropout`超參數：前者定義 dropout 率，應用到所有輸入上（每個時間步），后者定義 dropout 率，應用到隱藏態上（也是每個時間步）。無需在 RNN 中創建自定義單元來應用 dropout。 有了這些方法，就可以減輕不穩定梯度問題，高效訓練 RNN 了。下面來看如何處理短期記憶問題。 ### 處理短期記憶問題 由于數據在 RNN 中流動時會經歷轉換，每個時間步都損失了一定信息。一定時間后，第一個輸入實際上會在 RNN 的狀態中消失。就像一個攪局者。比如《尋找尼莫》中的多莉想翻譯一個長句：當她讀完這句話時，就把開頭忘了。為了解決這個問題，涌現出了各種帶有長期記憶的單元。首先了解一下最流行的一種：長短時記憶神經單元 LSTM。 ## LSTM 單元 長短時記憶單元在 1997 年[由 Sepp Hochreiter 和 Jürgen Schmidhuber 首次提出](https://links.jianshu.com/go?to=https%3A%2F%2Fgoo.gl%2Fj39AGv)，并在接下來的幾年內經過 [Alex Graves](https://links.jianshu.com/go?to=https%3A%2F%2Fhoml.info%2Fgraves)、[Ha?im Sak](https://links.jianshu.com/go?to=https%3A%2F%2Fhoml.info%2F94)、[Wojciech Zaremba](https://links.jianshu.com/go?to=https%3A%2F%2Fhoml.info%2F95) 等人的改進，逐漸完善。如果把 LSTM 單元看作一個黑盒，可以將其當做基本單元一樣來使用，但 LSTM 單元比基本單元性能更好：收斂更快，能夠感知數據的長時依賴。在 Keras 中，可以將`SimpleRNN`層，替換為`LSTM`層： ```py model = keras.models.Sequential([ keras.layers.LSTM(20, return_sequences=True, input_shape=[None, 1]), keras.layers.LSTM(20, return_sequences=True), keras.layers.TimeDistributed(keras.layers.Dense(10)) ]) ``` 或者，可以使用通用的`keras.layers.RNN layer`，設置`LSTMCell`參數： ```py model = keras.models.Sequential([ keras.layers.RNN(keras.layers.LSTMCell(20), return_sequences=True, input_shape=[None, 1]), keras.layers.RNN(keras.layers.LSTMCell(20), return_sequences=True), keras.layers.TimeDistributed(keras.layers.Dense(10)) ]) ``` 但是，當在 GPU 運行時，LSTM 層使用了優化的實現（見第 19 章），所以更應該使用 LSTM 層（`RNN`大多用來自定義層）。 LSTM 單元的工作機制是什么呢？圖 15-9 展示了 LSTM 單元的結構。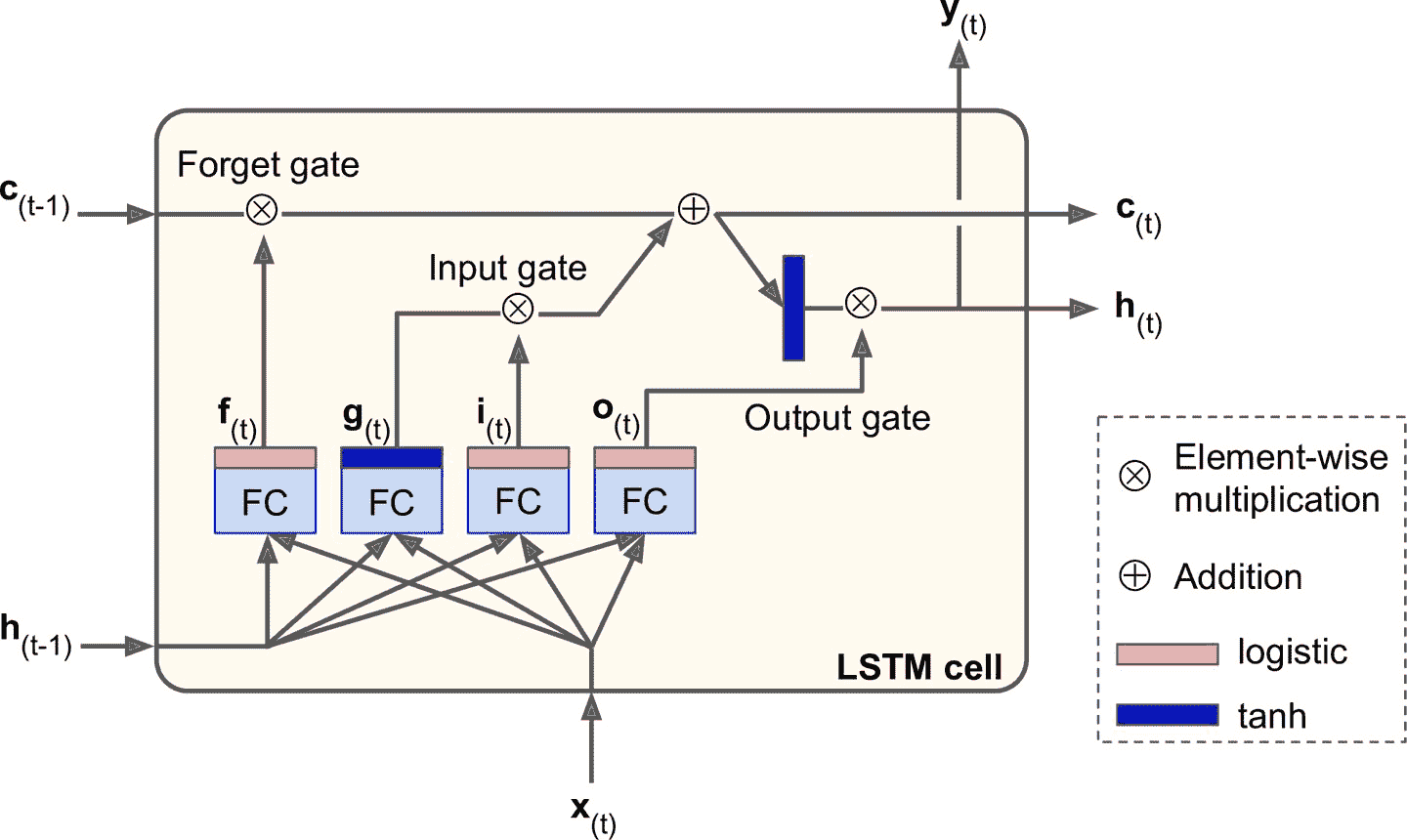 圖 15-9 LSTM 單元 如果不觀察黑箱的內部，LSTM 單元跟常規單元看起來差不多，除了 LSTM 單元的狀態分成了兩個矢量：h_(t) 和 c_(t)（`c`代表 cell）。可以認為 h_(t) 是短期記憶狀態，c_(t) 是長期記憶狀態。 現在打開黑箱。LSTM 單元的核心思想是它能從長期狀態中學習該存儲什么、丟掉什么、讀取什么。當長期狀態 c_(t-1) 從左向右在網絡中傳播，它先經過遺忘門（forget gate），丟棄一些記憶，之后通過添加操作增加一些記憶（從輸入門中選擇一些記憶）。結果 c_(t) 不經任何轉換直接輸出。因此，在每個時間步，都有一些記憶被拋棄，也有新的記憶添加進來。另外，添加操作之后，長時狀態復制后經過 tanh 激活函數，然后結果被輸出門過濾。得到短時狀態 h_(t)（它等于這一時間步的單元輸出， y_(t)。接下來討論新的記憶如何產生，門是如何工作的。 首先，當前的輸入矢量 x_(t) 和前一時刻的短時狀態 h_(t-1) 作為輸入，傳給四個不同的全連接層，這四個全連接層有不同的目的： * 輸出 g_(t)的層是主要層。它的常規任務是分析當前的輸入 x_(t) 和前一時刻的短時狀態 h_(t-1)。基本單元中與這種結構一樣，直接輸出了 h_(t) 和 y_(t) 。相反的，LSTM 單元中的該層的輸出不會直接出去，兒是將最重要的部分保存在長期狀態中（其余部分丟掉）。 * 其它三個全連接層被是門控制器（gate controller）。其采用 Logistic 作為激活函數，輸出范圍在 0 到 1 之間。可以看到，這三個層的輸出提供給了逐元素乘法操作，當輸入為 0 時門關閉，輸出為 1 時門打開。具體講： * 遺忘門（由 f_(t) 控制）決定哪些長期記憶需要被刪除； * 輸入門（由 i_(t) 控制） 決定哪部分 g_(t) 應該被添加到長時狀態中。 * 輸出門（由 o_(t) 控制）決定長時狀態的哪些部分要讀取和輸出為 h_(t) 和 y_(t)。 總而言之，LSTM 單元能夠學習識別重要輸入（輸入門的作用），存儲進長時狀態，并保存必要的時間（遺忘門功能），并在需要時提取出來。這解釋了為什么 LSTM 單元能夠如此成功地獲取時間序列、長文本、錄音等數據中的長期模式。 公式 15-3 總結了如何計算單元的長時狀態，短時狀態，和單個實例的在每個時間步的輸出（小批次的公式和這個公式很像）。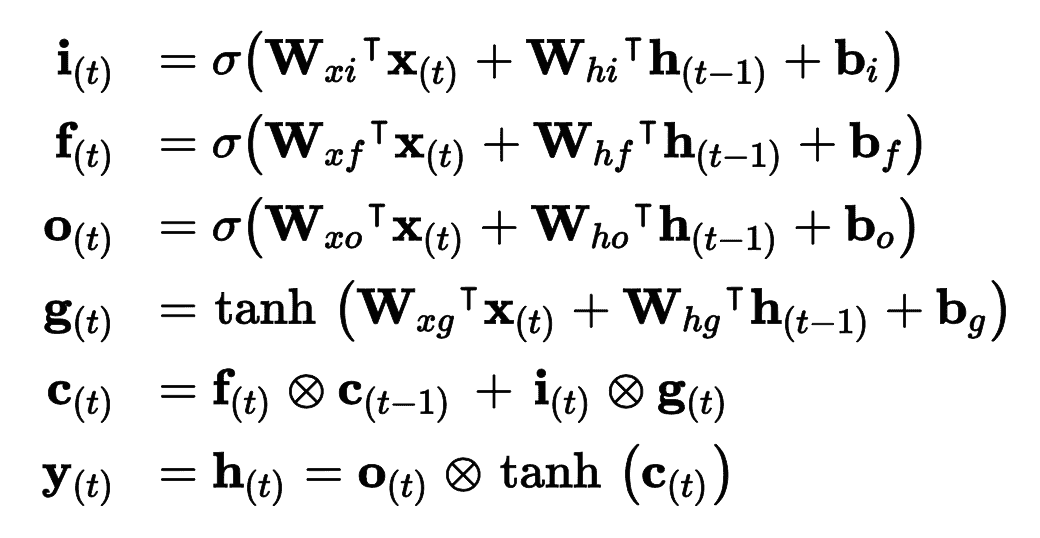 公式 15-3 LSTM 計算 在這個公式中， * W_xi，W_xf，W_xo，W_xg 是四個全連接層連接輸入向量 x_(t) 的權重。 * W_hi，W_hf，W_ho，W_hg 是四個全連接層連接上一時刻的短時狀態 h_(t-1) 的權重。 * b_i，b_f，b_o，b_g是全連接層的四個偏置項。需要注意的是 TensorFlow 將 b_f初始化為全 1 向量，而非全 0。這樣可以保證在訓練狀態開始時，忘掉所有東西。 ### 窺孔連接 在基本 LSTM 單元中，門控制器只能觀察當前輸入 x_(t) 和前一時刻的短時狀態 h_(t-1)。不妨讓各個門控制器窺視一下長時狀態，獲取一些上下文信息。[該想法](https://links.jianshu.com/go?to=ftp.idsia.ch%2Fpub%2Fjuergen%2FTimeCount-IJCNN2000.pdf)由 Felix Gers 和 Jürgen Schmidhuber 在 2000 年提出。他們提出了一個 LSTM 的變體，帶有叫做窺孔連接的額外連接：把前一時刻的長時狀態 c_(t-1) 輸入給遺忘門和輸入門，當前時刻的長時狀態 c_(t)輸入給輸出門。這么做時常可以提高性能，但不一定每次都能有效，也沒有清晰的規律顯示哪種任務適合添加窺孔連接。 Keras 中，`LSTM`層基于`keras.layers.LSTMCell`單元，后者目前還不支持窺孔。但是，試驗性的`tf.keras.experimental.PeepholeLSTMCell`支持，所以可以創建一個`keras.layers.RNN`層，向構造器傳入`PeepholeLSTMCell`。 LSTM 有多種其它變體，其中特別流行的是 GRU 單元。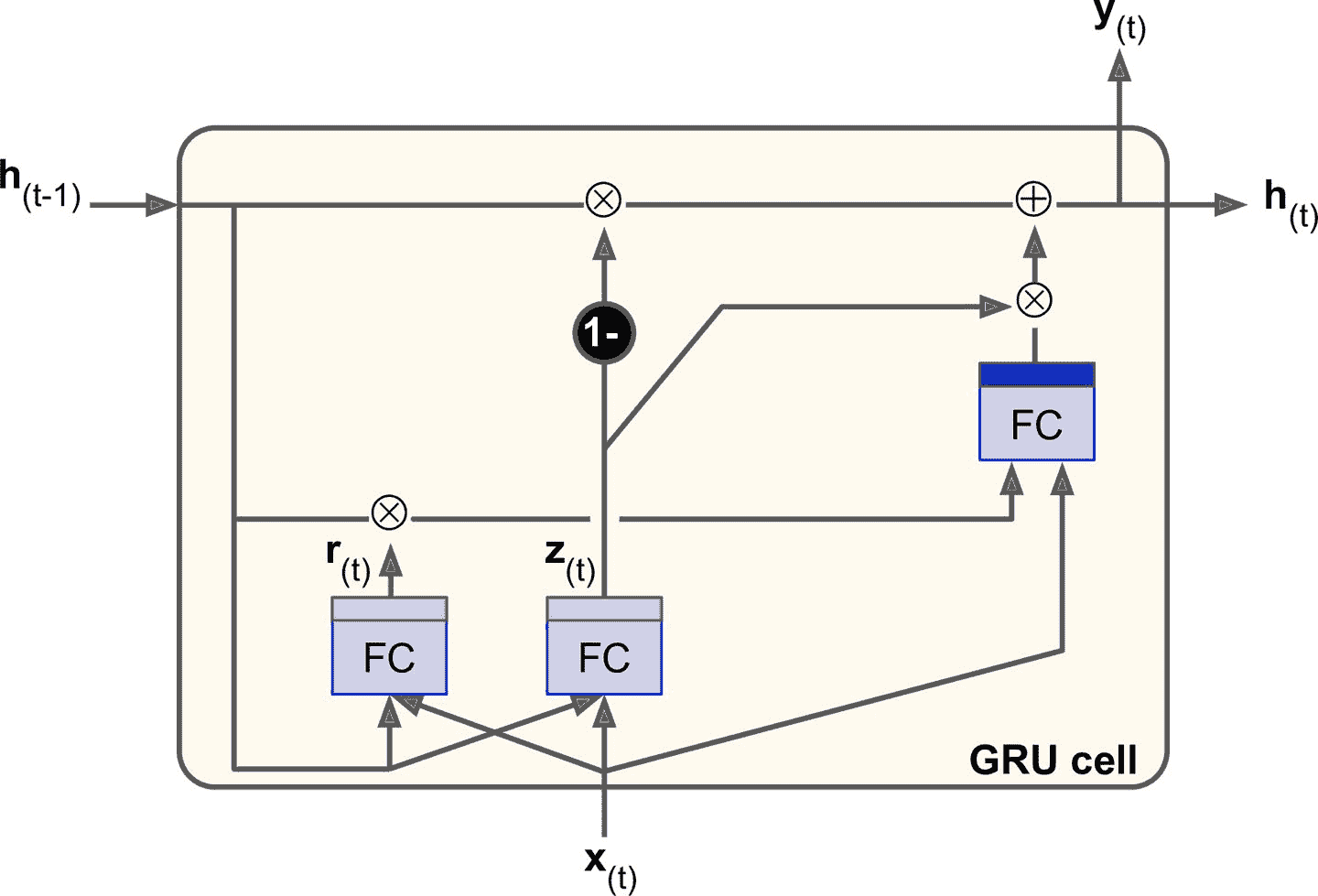 ### GRU 單元 圖 15-10 GRU 單元 門控循環單元（圖 15-10）在 2014 年的 [Kyunghyun Cho 的論文](https://links.jianshu.com/go?to=https%3A%2F%2Farxiv.org%2Fpdf%2F1406.1078v3.pdf)中提出，并且此文也引入了前文所述的編碼器-解碼器網絡。 GRU 單元是 LSTM 單元的簡化版本，能實現同樣的性能（這也說明了為什么它能越來越流行）。簡化主要在一下幾個方面： * 長時狀態和短時狀態合并為一個矢量 h_(t)。 * 用一個門控制器 z_(t)控制遺忘門和輸入門。如果門控制器輸出 1，則遺忘門打開（=1），輸入門關閉（1 - 1 = 0）。如果輸出 0，則相反。換句話說，如果當有記憶要存儲，那么就必須先在其存儲位置刪掉該處記憶。這構成了 LSTM 本身的常見變體。 * GRU 單元取消了輸出門，每個時間步輸出全態矢量。但是，增加了一個控制門 r_(t) 來控制前一狀態的哪些部分呈現給主層 g_(t)。 公式 15-4 總結了如何計算單元對單個實例在每個時間步的狀態。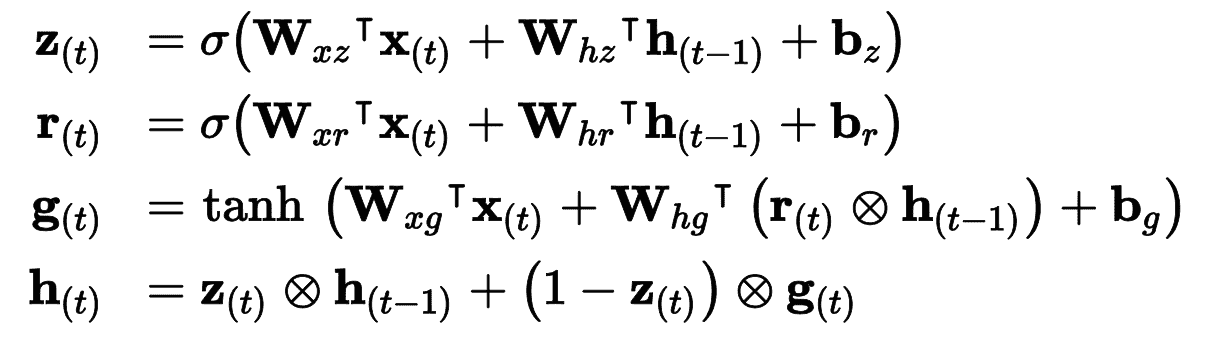 公式 15-4 GRU 計算 Keras 提供了`keras.layers.GRU`層（基于`keras.layers.GRUCell`記憶單元）；使用時，只需將`SimpleRNN`或`LSTM`替換為`GRU`。 LSTM 和 GRU 是 RNN 取得成功的主要原因之一。盡管它們相比于簡單 RNN 可以處理更長的序列了，還是有一定程度的短時記憶，序列超過 100 時，比如音頻、長時間序列或長序列，學習長時模式就很困難。應對的方法之一，是使用縮短輸入序列，例如使用 1D 卷積層。 ### 使用 1D 卷積層處理序列 在第 14 章中，我們使用 2D 卷積層，通過在圖片上滑動幾個小核（或過濾器），來產生多個 2D 特征映射（每個核產生一個）。相似的，1D 軍幾層在序列上滑動幾個核，每個核可以產生一個 1D 特征映射。每個核能學到一個非常短序列模式（不會超過核的大小）。如果你是用 10 個核，則輸出會包括 10 個 1 維的序列（長度相同），或者可以將輸出當做一個 10 維的序列。這意味著，可以搭建一個由循環層和 1D 卷積層（或 1 維池化層）混合組成的神經網絡。如果 1D 卷積層的步長是 1，填充為零，則輸出序列的長度和輸入序列相同。但如果使用`"valid"`填充，或大于 1 的步長，則輸出序列會比輸入序列短，所以一定要按照目標作出調整。例如，下面的模型和之前的一樣，除了開頭是一個步長為 2 的 1D 卷積層，用因子 2 對輸入序列降采樣。核大小比步長大，所以所有輸入會用來計算層的輸出，所以模型可以學到保存有用的信息、丟棄不重要信息。通過縮短序列，卷積層可以幫助 GRU 檢測長模式。注意，必須裁剪目標中的前三個時間步（因為核大小是 4，卷積層的第一個輸出是基于輸入時間步 0 到 3），并用因子 2 對目標做降采樣： ```py model = keras.models.Sequential([ keras.layers.Conv1D(filters=20, kernel_size=4, strides=2, padding="valid", input_shape=[None, 1]), keras.layers.GRU(20, return_sequences=True), keras.layers.GRU(20, return_sequences=True), keras.layers.TimeDistributed(keras.layers.Dense(10)) ]) model.compile(loss="mse", optimizer="adam", metrics=[last_time_step_mse]) history = model.fit(X_train, Y_train[:, 3::2], epochs=20, validation_data=(X_valid, Y_valid[:, 3::2])) ``` 如果訓練并評估這個模型，你會發現它是目前最好的模型。卷積層確實發揮了作用。事實上，可以只使用 1D 卷積層，不用循環層！ ### WaveNet 在一篇 2016 年的[論文](https://links.jianshu.com/go?to=https%3A%2F%2Fhoml.info%2Fwavenet)中，Aaron van den Oord 和其它 DeepMind 的研究者，提出了一個名為 WaveNet 的架構。他們將 1D 卷積層疊起來，每一層膨脹率（如何將每個神經元的輸入分開）變為 2 倍：第一個卷積層一次只觀察兩個時間步，，接下來的一層觀察四個時間步（感受野是 4 個時間步的長度），下一層觀察八個時間步，以此類推（見圖 15-11）。用這種方式，底下的層學習短時模式，上面的層學習長時模式。得益于翻倍的膨脹率，這個網絡可以非常高效地處理極長的序列。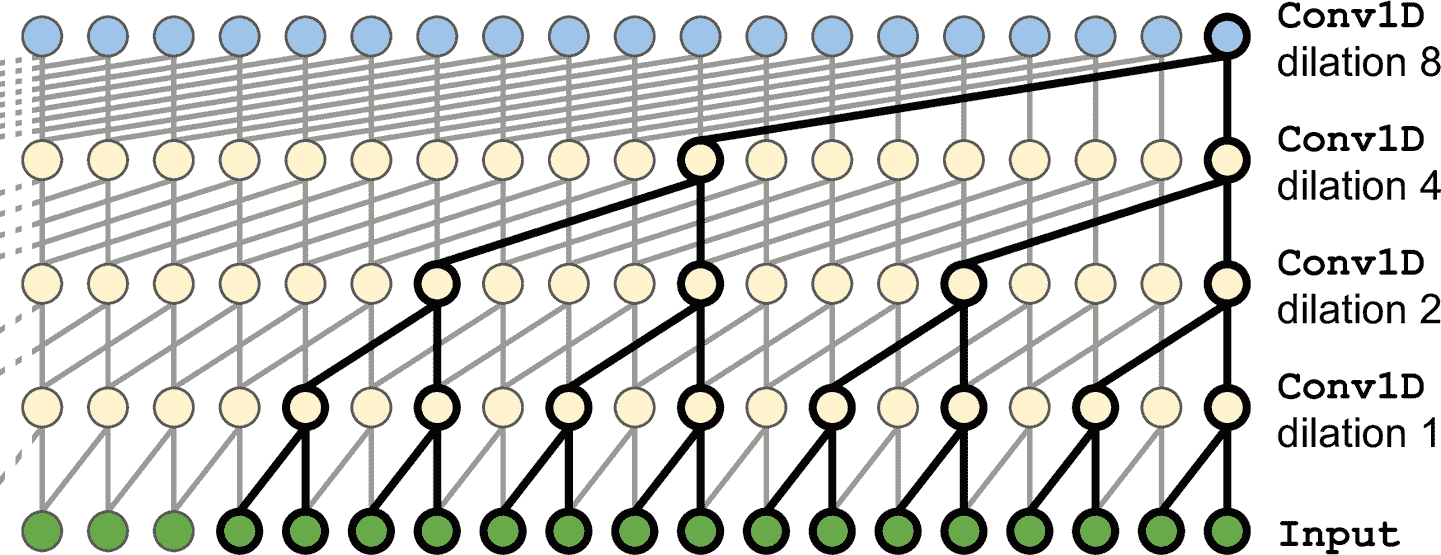 圖 15-11 WaveNet 架構 在 WaveNet 論文中，作者疊了 10 個卷積層，膨脹率為 1, 2, 4, 8, …, 256, 512，然后又疊了一組 10 個相同的層（膨脹率還是 1, 2, 4, 8, …, 256, 512），然后又是 10 個相同的層。作者解釋到，一摞這樣的 10 個卷積層，就像一個超高效的核大小為 1024 的卷積層（只是更快、更強、參數更少），所以同樣的結構疊了三次。他們還給輸入序列左填充了一些 0，以滿足每層的膨脹率，使序列長度不變。下面的代碼實現了簡化的 WaveNet，來處理前面的序列： ```py model = keras.models.Sequential() model.add(keras.layers.InputLayer(input_shape=[None, 1])) for rate in (1, 2, 4, 8) * 2: model.add(keras.layers.Conv1D(filters=20, kernel_size=2, padding="causal", activation="relu", dilation_rate=rate)) model.add(keras.layers.Conv1D(filters=10, kernel_size=1)) model.compile(loss="mse", optimizer="adam", metrics=[last_time_step_mse]) history = model.fit(X_train, Y_train, epochs=20, validation_data=(X_valid, Y_valid)) ``` `Sequential`模型開頭是一個輸入層（比只在第一個層上設定`input_shape`簡單的多）；然后是一個 1D 卷積層，使用`"causal"`填充：這可以保證卷積層在做預測時，不會窺視到未來值（等價于在輸入序列的左邊用零填充填充合適數量的 0）。然后添加相似的成對的層，膨脹率為 1、2、4、8，接著又是 1、2、4、8。最后，添加輸出層：一個有 10 個大小為 1 的過濾器的卷積層，沒有激活函數。得益于填充層，每個卷積層輸出的序列長度都和輸入序列一樣，所以訓練時的目標可以是完整序列：無需裁剪或降采樣。 最后兩個模型的序列預測結果最好！在 WaveNet 論文中，作者在多種音頻任務（WaveNet 名字正是源于此）中，包括文本轉語音任務（可以輸出多種語言極為真實的語音），達到了頂尖的表現。他們還用這個模型生成音樂，每次生成一段音頻。每段音頻包含上萬個時間步（LSTM 和 GRU 無法處理如此長的序列），這是相當了不起的。 第 16 章，我們會繼續探索 RNN，會看到如何用 RNN 處理各種 NLP 任務。 ## 練習 1. 你能說出序列到序列 RNN 的幾個應用嗎？序列到矢量的應用？矢量到序列的應用？ 2. RNN 層的輸入要有多少維？每一維表示什么？輸出呢？ 3. 如果搭建深度序列到序列 RNN，哪些 RNN 層要設置`return_sequences=True`？序列到矢量 RNN 又如何？ 4. 假如有一個每日單變量時間序列，想預測接下來的七天。要使用什么 RNN 架構？ 5. 訓練 RNN 的困難是什么？如何應對？ 6. 畫出 LSTM 單元的架構圖？ 7. 為什么在 RNN 中使用 1D 卷積層？ 8. 哪種神經網絡架構可以用來分類視頻？ 9. 為 SketchRNN 數據集（TensorFlow Datasets 中有），訓練一個分類模型。 10. 下載[Bach chorales](https://links.jianshu.com/go?to=https%3A%2F%2Fhoml.info%2Fbach)數據集，并解壓。它含有 382 首巴赫作曲的贊美歌。每首的長度是 100 到 640 時間步，每個時間步包含 4 個整數，每個整數對應一個鋼琴音符索引（除了 0，表示沒有音符）。訓練一個可以預測下一個時間步（四個音符）的模型，循環、卷積、或混合架構。然后使用這個模型來生成類似巴赫的音樂，每個時間一個音符：可以給模型一首贊美歌的開頭，然后讓其預測接下來的時間步，然后將輸出加到輸入上，再讓模型繼續預測。或者查看[Google 的 Coconet 模型](https://links.jianshu.com/go?to=https%3A%2F%2Fhoml.info%2Fcoconet)，它是 Google 來做巴赫曲子的。 參考答案見附錄 A。