# 十、使用 Keras 搭建人工神經網絡 > 譯者：[@SeanCheney](https://www.jianshu.com/u/130f76596b02) 鳥類啟發人類飛翔，東洋參啟發了魔術貼的發明，大自然啟發人類實現了無數發明創造。通過研究大腦來制造智能機器，也符合這個邏輯。人工神經網絡（ANN）就是沿著這條邏輯誕生的：人工神經網絡是受大腦中的生物神經元啟發而來的機器學習模型。但是，雖然飛機是受鳥兒啟發而來的，飛機卻不用揮動翅膀。相似的，人工神經網絡和生物神經元網絡也是具有不同點的。一些研究者甚至認為，應該徹底摒棄這種生物學類比：例如，用“單元”取代“神經元”，以免人們將創造力局限于生物學系統的合理性上。 人工神經網絡是深度學習的核心，它不僅樣式多樣、功能強大，還具有可伸縮性，這讓人工神經網絡適宜處理龐大且復雜的機器學習任務，例如對數十億張圖片分類（谷歌圖片）、語音識別（蘋果 Siri）、向數億用戶每天推薦視頻（Youtube）、或者通過學習幾百圍棋世界冠軍（DeepMind 的 AlphaGo）。 本章的第一部分會介紹人工神經網絡，從一個簡單的 ANN 架構開始，然后過渡到多層感知機（MLP），后者的應用非常廣泛（后面的章節會介紹其他的架構）。第二部分會介紹如何使用流行的 Keras API 搭建神經網絡，Keras API 是一個設計優美、簡單易用的高級 API，可以用來搭建、訓練、評估、運行神經網絡。Keras 的易用性，并不妨礙它具有強大的實現能力，Keras 足以幫你搭建多種多樣的神經網絡。事實上，Keras 足以完成大多數的任務啦！要是你需要實現更多的功能，你可以用 Keras 的低級 API（第 12 章介紹）自己寫一些組件。 # 從生物神經元到人工神經元 頗讓人驚訝的地方是，其實 ANN 已經誕生相當長時間了：神經生理學家 Warren McCulloch 和數學家 Walter Pitts 在 1943 年首次提出了 ANN。在他們里程碑的論文《A Logical Calculus of Ideas Immanent in Nervous Activity》中（[https://scholar.google.com/scholar?q=A+Logical+Calculus+of+Ideas+Immanent+in+Nervous+Activity+author%3Amcculloch](https://links.jianshu.com/go?to=https%3A%2F%2Fscholar.google.com%2Fscholar%3Fq%3DA%2BLogical%2BCalculus%2Bof%2BIdeas%2BImmanent%2Bin%2BNervous%2BActivity%2Bauthor%253Amcculloch)），McCulloch 和 Pitts 介紹一個簡單的計算模型，關于生物大腦的神經元是如何通過命題邏輯協同工作的。這是第一個 ANN 架構，后來才出現更多的 ANN 架構。 ANN 的早期成功讓人們廣泛相信，人類馬上就能造出真正的智能機器了。1960 年代，當這個想法落空時，資助神經網絡的錢銳減，ANN 進入了寒冬。1980 年代早期，誕生了新的神經網絡架構和新的訓練方法，連結主義（研究神經網絡）復蘇，但是進展很慢。到了 1990 年代，出現了一批強大的機器學習方法，比如支持向量機（見第 05 章）。這些新方法的結果更優，也比 ANN 具有更扎實的理論基礎，神經網絡研究又一次進入寒冬。我們正在經歷的是第三次神經網絡浪潮。這波浪潮會像前兩次那樣嗎？這次與前兩次有所不同，這一次會對我們的生活產生更大的影響，理由如下： * 我們現在有更多的數據，用于訓練神經網絡，在大而復雜的問題上，ANN 比其它 ML 技術表現更好； * 自從 1990 年代，計算能力突飛猛進，現在已經可以在理想的時間內訓練出大規模的神經網絡了。一部分原因是摩爾定律（在過去 50 年間，集成電路中的組件數每兩年就翻了一倍），另外要歸功于游戲產業，后者生產出了強大的 GPU 顯卡。還有，云平臺使得任何人都能使用這些計算能力； * 訓練算法得到了提升。雖然相比 1990 年代，算法變化不大，但這一點改進卻產生了非常大的影響； * 在實踐中，人工神經網絡的一些理論局限沒有那么強。例如，許多人認為人工神經網絡訓練算法效果一般，因為它們很可能陷入局部最優，但事實證明，這在實踐中是相當罕見的（或者如果它發生，它們也通常相當接近全局最優）； * ANN 已經進入了資助和進步的良性循環。基于 ANN 的驚艷產品常常上頭條，從而吸引了越來越多的關注和資金，促進越來越多的進步和更驚艷的產品。 ## 生物神經元 在討論人工神經元之前，先來看看生物神經元（見圖 10-1）。這是動物大腦中一種不太常見的細胞，包括：細胞體（含有細胞核和大部分細胞組織），許多貌似樹枝的樹突，和一條非常長的軸突。軸突的長度可能是細胞體的幾倍，也可能是一萬倍。在軸突的末梢，軸突分叉成為終樹突，終樹突的末梢是突觸，突觸連接著其它神經元的樹突或細胞體。 生物神經元會產生被稱為“動作電位”（或稱為信號）的短促電脈沖，信號沿軸突傳遞，使突觸釋放出被稱為神經遞質的化學信號。當神經元在幾毫秒內接收了足夠量的神經遞質，這個神經元也會發送電脈沖（事實上，要取決于神經遞質，一些神經遞質會禁止發送電脈沖）。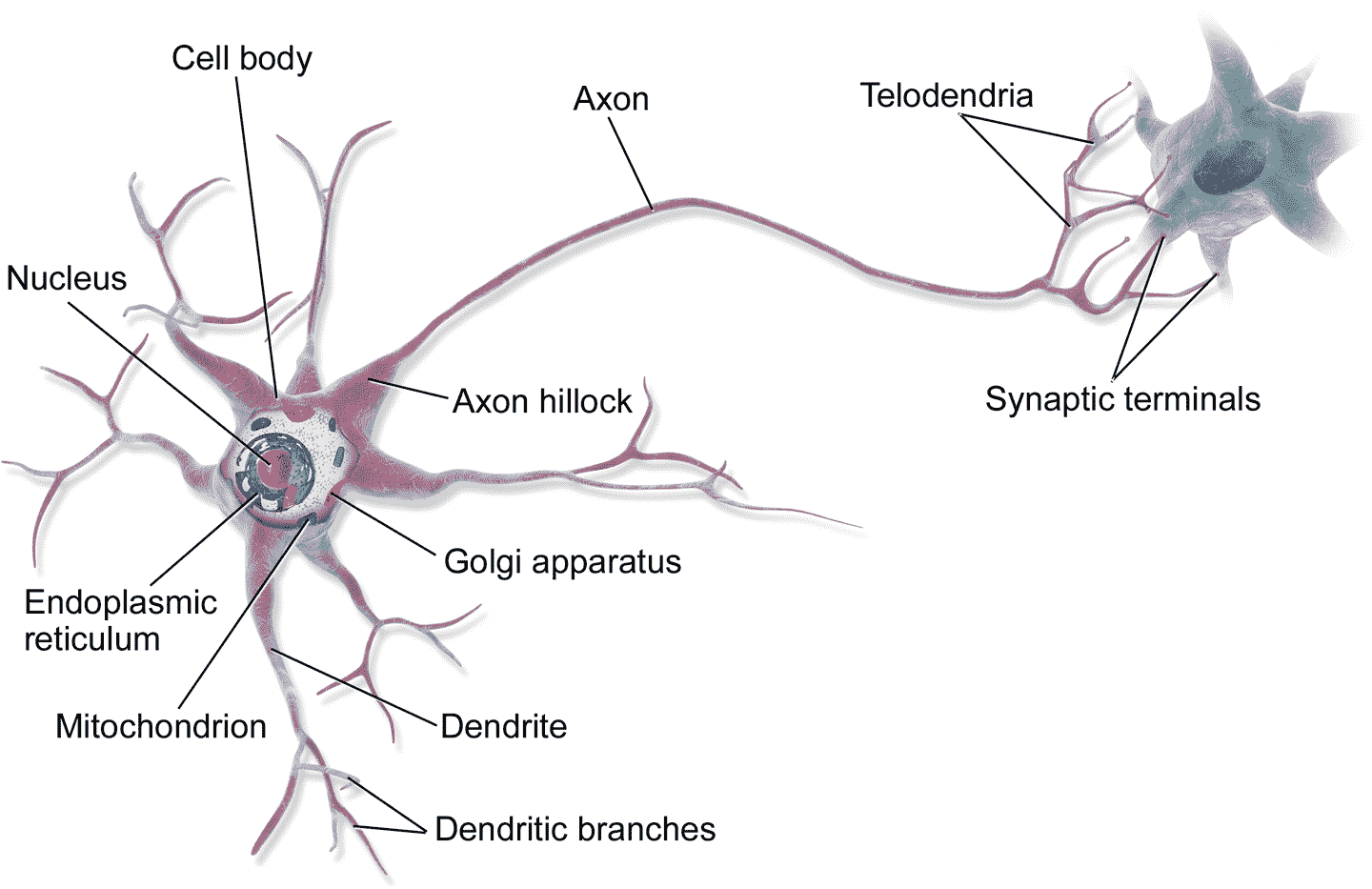 圖 10-1 生物神經元 獨立的生物神經元就是這樣工作的，但因為神經元是處于數十億神經元的網絡中的，每個神經元都連著幾千個神經元。簡單神經元的網絡可以完成高度復雜的計算，就好像螞蟻齊心協力就能建成復雜的蟻冢一樣。生物神經網絡（BNN）如今仍是活躍的研究領域，人們通過繪制出了部分大腦的結構，發現神經元分布在連續的皮層上，尤其是在大腦皮質上（大腦外層），見圖 10-2。 圖 10-2 人類大腦皮質的多層神經元網絡 ## 神經元的邏輯計算 McCulloch 和 Pitts 提出了一個非常簡單的生物神經元模型，它后來演化成了人工神經元：一個或多個二元（開或關）輸入，一個二元輸出。當達到一定的輸入量時，神經元就會產生輸出。在論文中，兩位作者證明就算用如此簡單的模型，就可以搭建一個可以完成任何邏輯命題計算的神經網絡。為了展示網絡是如何運行的，我們自己親手搭建一些不同邏輯計算的 ANN（見圖 10-3），假設有兩個活躍的輸入時，神經元就被激活。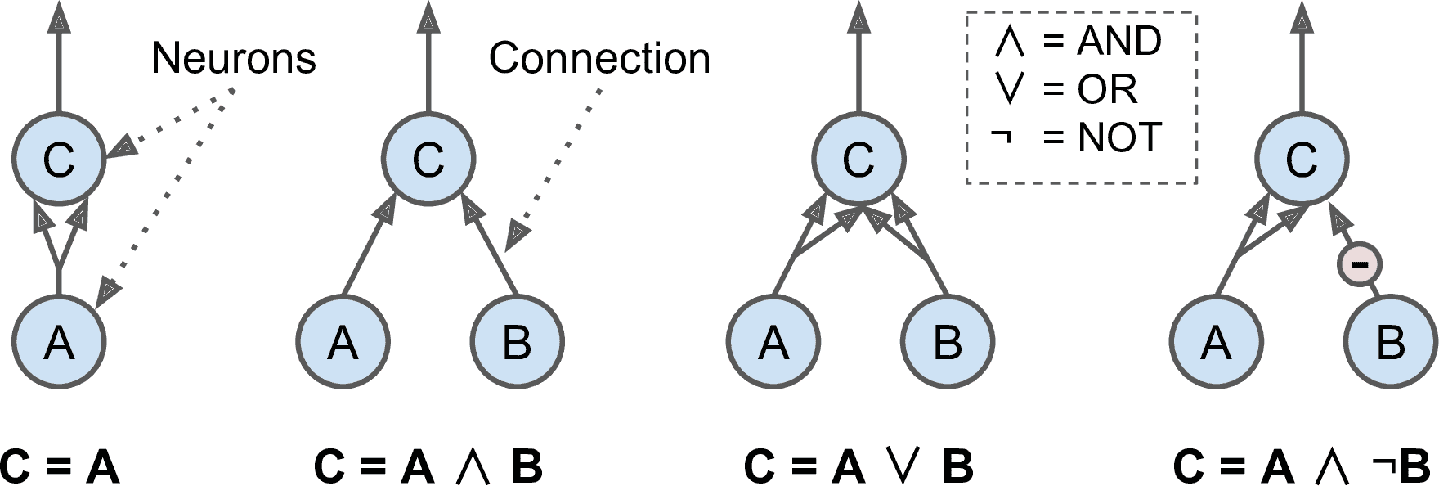 圖 10-3 不同邏輯計算的 ANN 這些網絡的邏輯計算如下： * 左邊第一個網絡是確認函數：如果神經元 A 被激活，那么神經元 C 也被激活（因為它接收來自神經元 A 的兩個輸入信號），但是如果神經元 A 關閉，那么神經元 C 也關閉。 * 第二個網絡執行邏輯 AND：神經元 C 只有在激活神經元 A 和 B（單個輸入信號不足以激活神經元 C）時才被激活。 * 第三個網絡執行邏輯 OR：如果神經元 A 或神經元 B 被激活（或兩者），神經元 C 被激活。 * 最后，如果我們假設輸入連接可以抑制神經元的活動（生物神經元是這樣的情況），那么第四個網絡計算一個稍微復雜的邏輯命題：如果神經元 B 關閉，只有當神經元 A 是激活的，神經元 C 才被激活。如果神經元 A 始終是激活的，那么你得到一個邏輯 NOT：神經元 C 在神經元 B 關閉時是激活的，反之亦然。 你可以很容易地想到，如何將這些網絡組合起來計算復雜的邏輯表達式（參見本章末尾的練習）。 ## 感知機 感知器是最簡單的人工神經網絡結構之一，由 Frank Rosenblatt 發明于 1957 年。它基于一種稍微不同的人工神經元（見圖 10-4），閾值邏輯單元（TLU），或稱為線性閾值單元（LTU）：輸入和輸出是數字（而不是二元開/關值），并且每個輸入連接都一個權重。TLU 計算其輸入的加權和（z = W₁x₁ + W₂x₂ + ... + W_nx_n = x^T·W），然后將階躍函數應用于該和，并輸出結果：h_W(x) = step(z)，其中 z = x^T·W。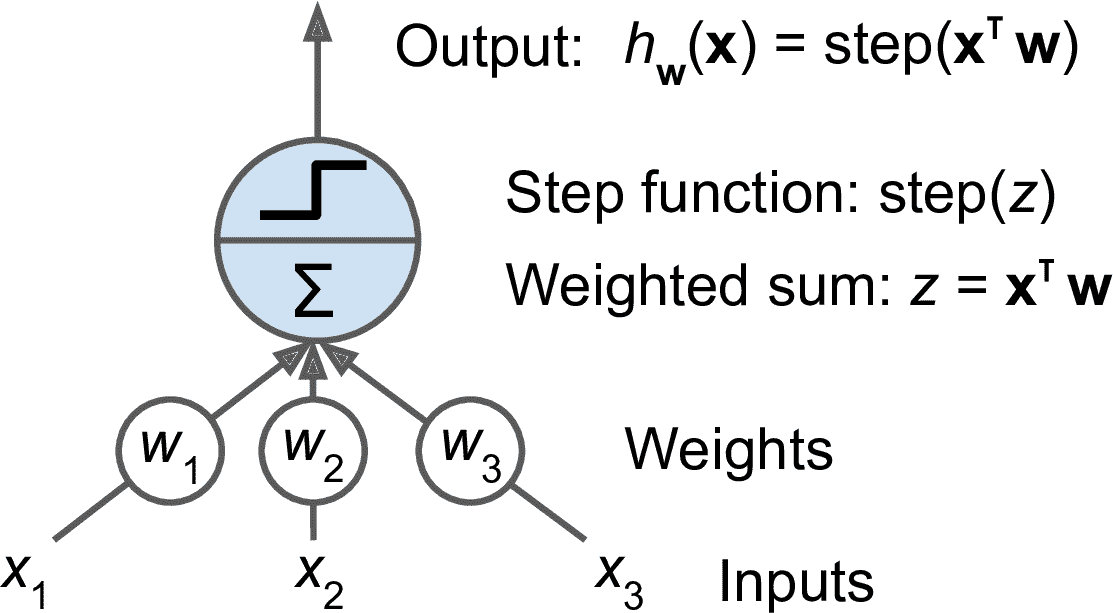 圖 10-4 閾值邏輯單元：人工神經元做權重求和，然后對和做階躍函數 感知機最常用的階躍函數是單位階躍函數（Heaviside step function），見公式 10-1。有時候也使用符號函數 sgn。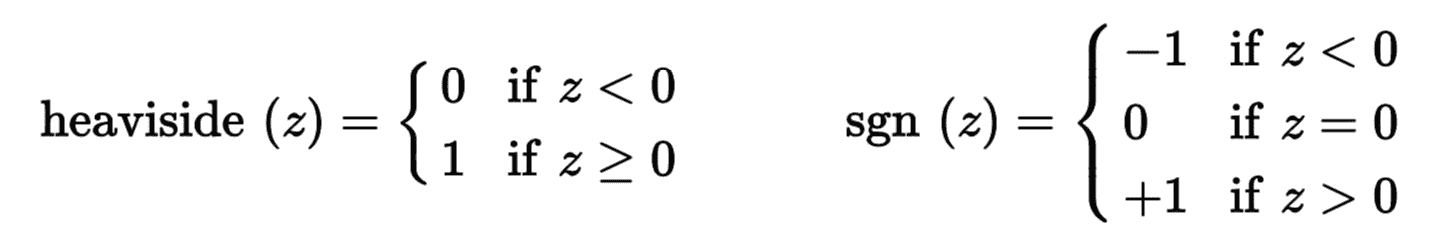 公式 10-1 感知機常用的階躍函數，閾值為 0 單一 TLU 可用于簡單的線性二元分類。它計算輸入的線性組合，如果結果超過閾值，它輸出正類或者輸出負類（就像邏輯回歸分類或線性 SVM 分類）。例如，你可以使用單一 TLU，基于花瓣長度和寬度分類鳶尾花（也可添加額外的偏置特征 x₀=1，就像我們在前面章節所做的那樣）。訓練 TLU 意味著去尋找合適的 W₀、W₁和 W₂值（訓練算法稍后提到）。 感知器只由一層 TLU 組成，每個 TLU 連接到所有輸入。當一層的神經元連接著前一層的每個神經元時，該層被稱為全連接層，或緊密層。感知機的輸入來自輸入神經元，輸入神經元只輸出從輸入層接收的任何輸入。所有的輸入神經元位于輸入層。此外，通常再添加一個偏置特征（X₀=1）：這種偏置特性通常用一種稱為偏置神經元的特殊類型的神經元來表示，它總是輸出 1。圖 10-5 展示了一個具有兩個輸入和三個輸出的感知機，它可以將實例同時分成為三個不同的二元類，這使它成為一個多輸出分類器。。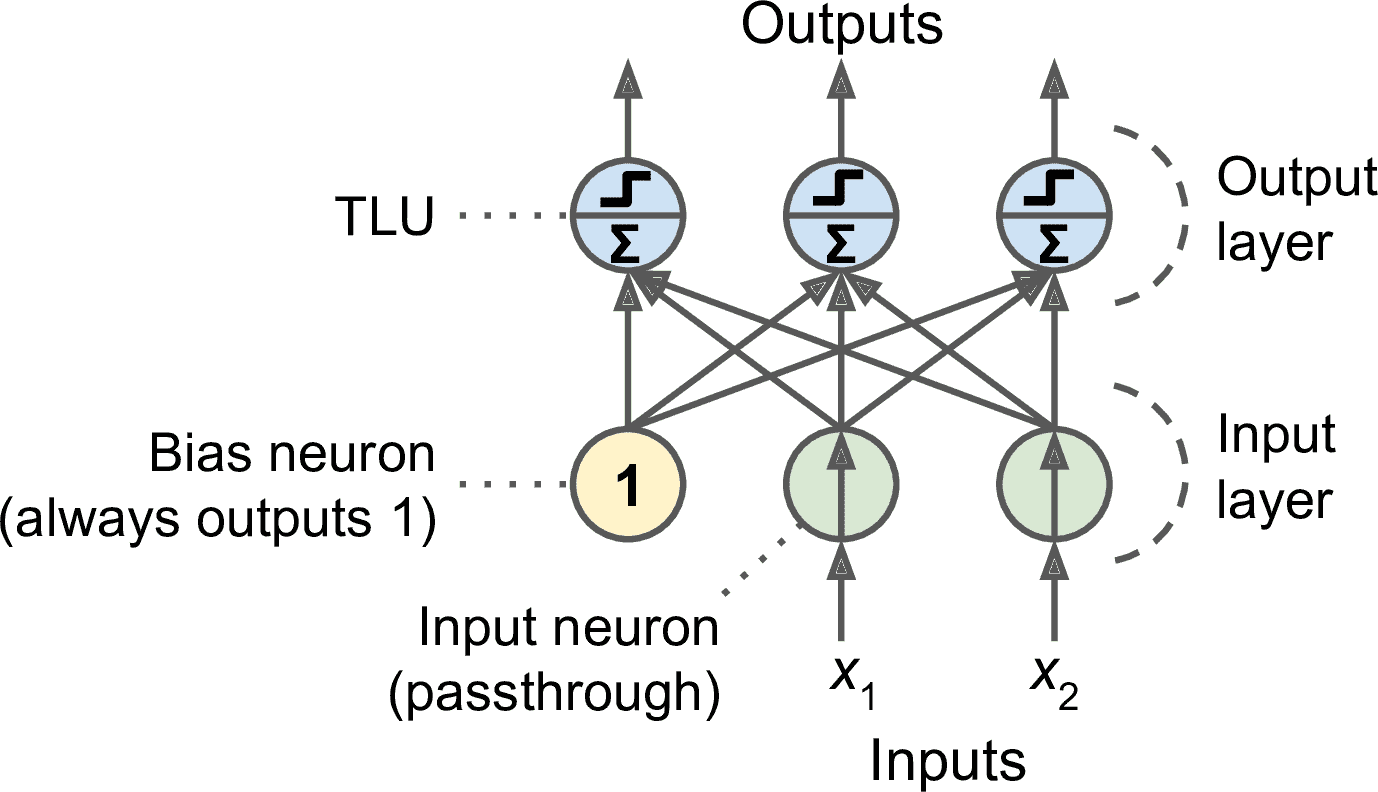 圖 10-5 一個具有兩個輸入神經元、一個偏置神經元和三個輸出神經元的感知機架構 借助線性代數，利用公式 10-2 可以方便地同時算出幾個實例的一層神經網絡的輸出。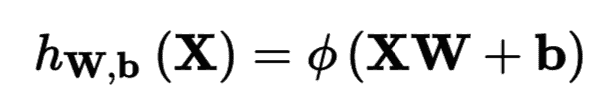 公式 10-2 計算一個全連接層的輸出 在這個公式中， * `X`表示輸入特征矩陣，每行是一個實例，每列是一個特征； * 權重矩陣`W`包含所有的連接權重，除了偏置神經元。每有一個輸入神經元權重矩陣就有一行，神經層每有一個神經元權重矩陣就有一列； * 偏置矢量`b`含有所有偏置神經元和人工神經元的連接權重。每有一個人工神經元就對應一個偏置項； * 函數被稱為激活函數，當人工神經網絡是 TLU 時，激活函數是階躍函數（后面會討論更多的激活函數）。 那么感知器是如何訓練的呢？Frank Rosenblatt 提出的感知器訓練算法在很大程度上受到 Hebb 規則的啟發。在 1949 出版的《行為組織》一書中，Donald Hebb 提出，當一個生物神經元經常觸發另一個神經元時，這兩個神經元之間的聯系就會變得更強。這個想法后來被 Siegrid L?wel 總結為一經典短語：“一起燃燒的細胞，匯合在一起。”這個規則后來被稱為 Hebb 規則（或 Hebbian learning）。使用這個規則的變體來訓練感知器，該規則考慮了網絡所犯的誤差。更具體地，感知器一次被饋送一個訓練實例，對于每個實例，它進行預測。對于每一個產生錯誤預測的輸出神經元，修正輸入的連接權重，以獲得正確的預測。公式 10-3 展示了 Hebb 規則。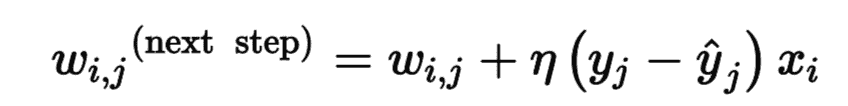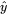 公式 10-3 感知機的學習規則（權重更新） 在這個公式中： * 其中 w_i,j是第`i`個輸入神經元與第`j`個輸出神經元之間的連接權重； * x_i是當前訓練實例的第`i`個輸入值； * _j是當前訓練實例的第`j`個輸出神經元的輸出； * y_j是當前訓練實例的第`j`個輸出神經元的目標輸出； * η是學習率。 每個輸出神經元的決策邊界是線性的，因此感知器不能學習復雜的模式（比如 Logistic 回歸分類器）。然而，如果訓練實例是線性可分的，Rosenblatt 證明該算法將收斂到一個解。這被稱為感知器收斂定理。 Scikit-Learn 提供了一個 Perceptron 類，它實現了一個 單 TLU 網絡。它可以實現大部分功能，例如用于 iris 數據集（第 4 章中介紹過）： ```py import numpy as np from sklearn.datasets import load_iris from sklearn.linear_model import Perceptron iris = load_iris() X = iris.data[:, (2, 3)] # petal length, petal width y = (iris.target == 0).astype(np.int) # Iris setosa? per_clf = Perceptron() per_clf.fit(X, y) y_pred = per_clf.predict([[2, 0.5]]) ``` 你可能注意到，感知器學習算法和隨機梯度下降很像。事實上，sklearn 的`Perceptron`類相當于使用具有以下超參數的 `SGDClassifier`：`loss="perceptron"`，`learning_rate="constant"`，`eta0=1`（學習率），`penalty=None`（無正則化）。 與邏輯回歸分類器相反，感知機不輸出類概率，而是基于硬閾值進行預測。這是邏輯回歸優于感知機的一點。 在 1969 年題為“感知機”的專著中，Marvin Minsky 和 Seymour Papert 強調了感知器的許多嚴重缺陷，特別是它們不能解決一些瑣碎的問題（例如，異或（XOR）分類問題）；參見圖 10-6 的左側）。當然，其他的線性分類模型（如 Logistic 回歸分類器）也都實現不了，但研究人員期望從感知器中得到更多，他們的失望是很大的，導致許多人徹底放棄了神經網絡，而是轉向高層次的問題，如邏輯、問題解決和搜索。 然而，事實證明，感知機的一些局限性可以通過堆疊多個感知機消除。由此產生的人工神經網絡被稱為多層感知機（MLP）。特別地，MLP 可以解決 XOR 問題，你可以通過計算圖 10-6 右側所示的 MLP 的輸出來驗證輸入的每一個組合：輸入(0, 0)或(1, 1)網絡輸出 0，輸入(0, 1)或(1, 0)它輸出 1。除了四個連接的權重不是 1，其它連接都是 1。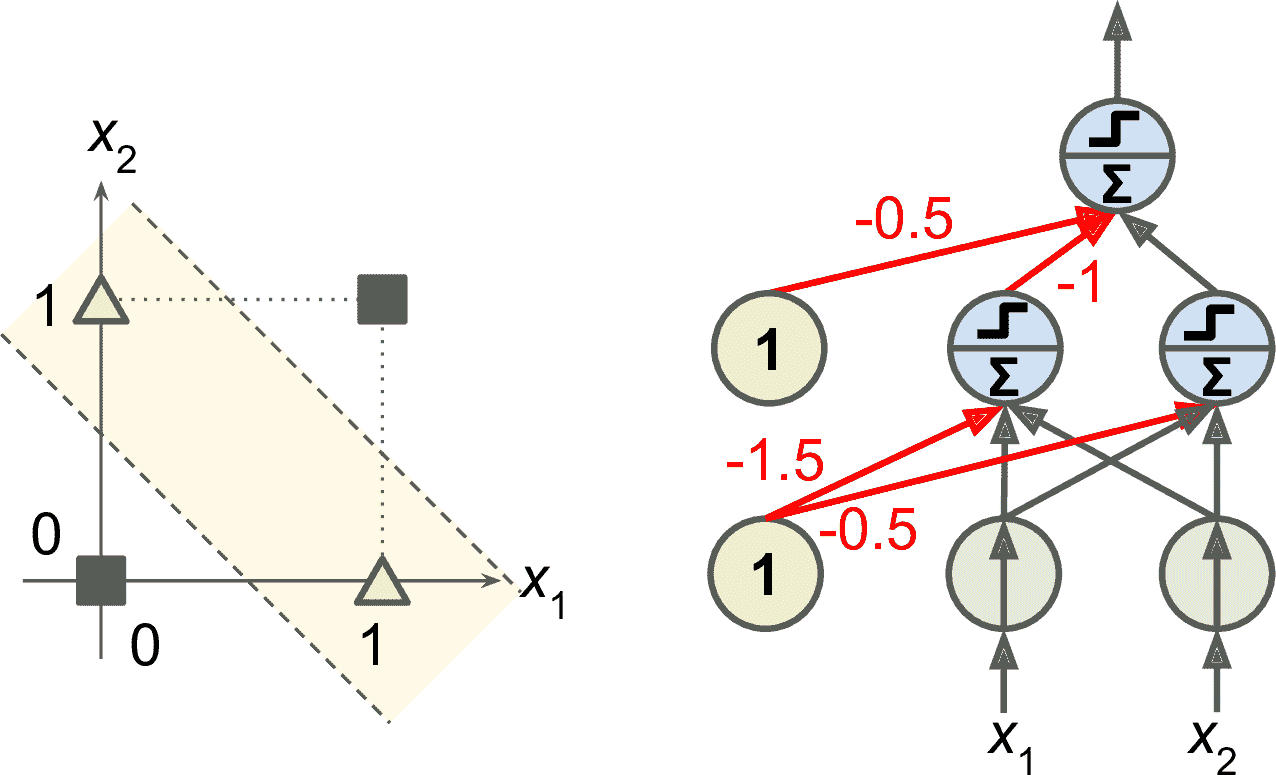 圖 10-6 XOR 分類問題和 MLP ## 多層感知機與反向傳播 MLP 由一個輸入層、一個或多個稱為隱藏層的 TLU 組成，一個 TLU 層稱為輸出層（見圖 10-7）。靠近輸入層的層，通常被稱為淺層，靠近輸出層的層通常被稱為上層。除了輸出層，每一層都有一個偏置神經元，并且全連接到下一層。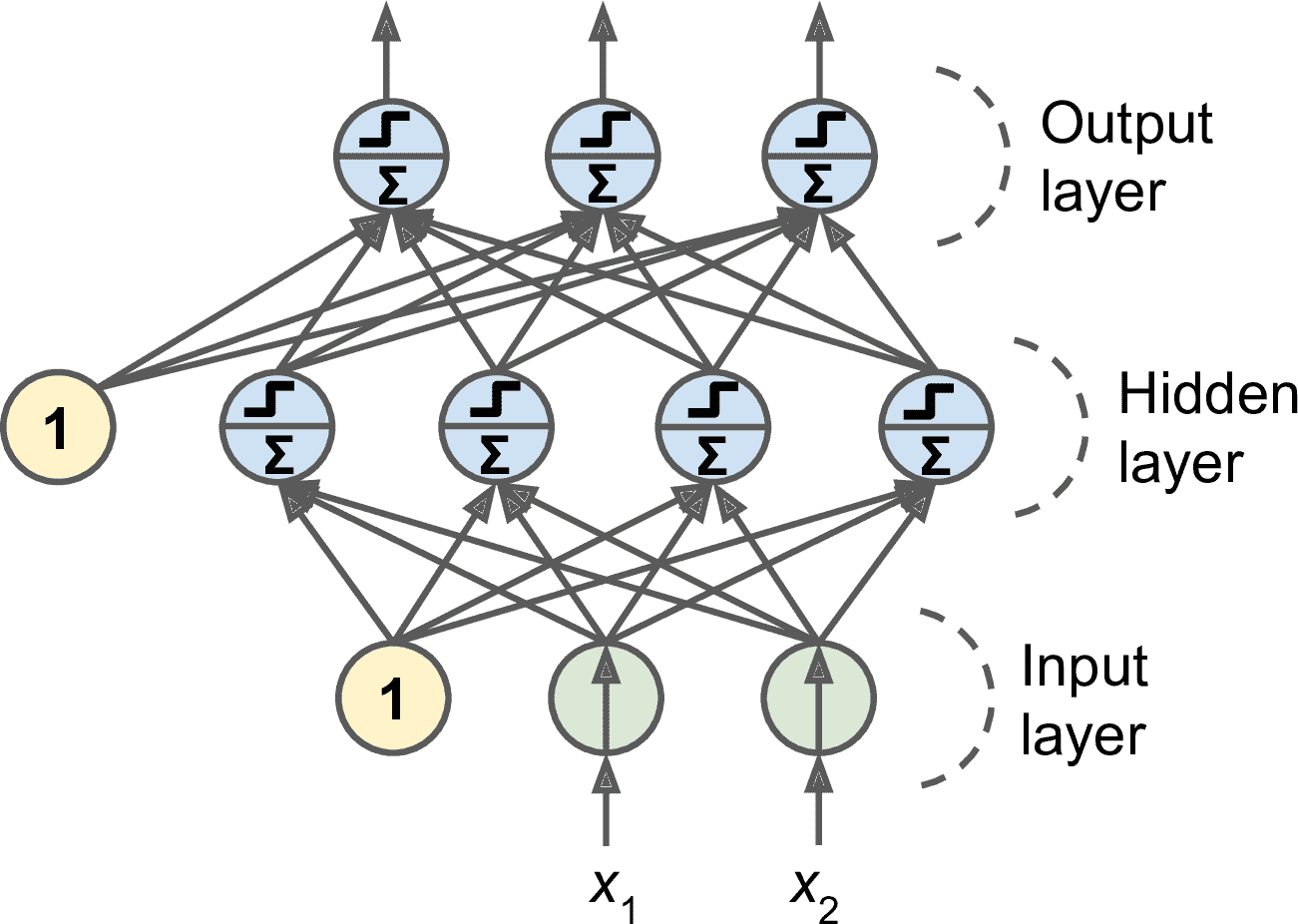 圖 10-7 多層感知器 > 注意：信號是從輸入到輸出單向流動的，因此這種架構被稱為前饋神經網絡（FNN）。 當人工神經網絡有多個隱含層時，稱為深度神經網絡（DNN）。深度學習研究的是 DNN 和深層計算模型。但是大多數人用深度學習泛化代替神經網絡，即便網絡很淺時。 多年來，研究人員努力尋找一種訓練 MLP 的方法，但沒有成功。但在 1986，David Rumelhart、Geoffrey Hinton、Ronald Williams 發表了一篇突破性的論文（[https://scholar.google.com/scholar?q=Learning+Internal+Representations+by+Error+Propagation+author%3Arumelhart](https://links.jianshu.com/go?to=https%3A%2F%2Fscholar.google.com%2Fscholar%3Fq%3DLearning%2BInternal%2BRepresentations%2Bby%2BError%2BPropagation%2Bauthor%253Arumelhart)），提出了至今仍在使用的反向傳播訓練算法。總而言之，反向傳播算法是使用了高效梯度計算的梯度下降算法（見第 4 章）：只需要兩次網絡傳播（一次向前，一次向后），就可以算出網絡誤差的、和每個獨立模型參數相關的梯度。換句話說，反向傳播算法為了減小誤差，可以算出每個連接權重和每個偏置項的調整量。當得到梯度之后，就做一次常規的梯度下降，不斷重復這個過程，直到網絡得到收斂解。 > 筆記：自動計算梯度被稱為自動微分。有多種自動微分的方法，各有優缺點。反向傳播使用的是反向模式自微分。這種方法快而準，當函數有多個變量（連接權重）和多個輸出（損失函數）要微分時也能應對。附錄 D 介紹了自微分。 對 BP 做詳細分解： * 每次處理一個微批次（假如每個批次包含 32 個實例），用訓練集多次訓練 BP，每次被稱為一個周期（epoch）； * 每個微批次先進入輸入層，輸入層再將其發到第一個隱藏層。計算得到該層所有神經元的（微批次的每個實例的）輸出。輸出接著傳到下一層，直到得到輸出層的輸出。這個過程就是前向傳播：就像做預測一樣，只是保存了每個中間結果，中間結果要用于反向傳播； * 然后計算輸出誤差（使用損失函數比較目標值和實際輸出值，然后返回誤差）； * 接著，計算每個輸出連接對誤差的貢獻量。這是通過鏈式法則（就是對多個變量做微分的方法）實現的； * 然后還是使用鏈式法則，計算最后一個隱藏層的每個連接對誤差的貢獻，這個過程不斷向后傳播，直到到達輸入層。 * 最后，BP 算法做一次梯度下降步驟，用剛剛計算的誤差梯度調整所有連接權重。 BP 算法十分重要，再歸納一下：對每個訓練實例，BP 算法先做一次預測（前向傳播），然后計算誤差，然后反向通過每一層以測量誤差貢獻量（反向傳播），最后調整所有連接權重以降低誤差（梯度下降）。（譯者注：我也總結下吧，每次訓練都先是要設置周期 epoch 數，每次 epoch 其實做的就是三件事，向前傳一次，向后傳一次，然后調整參數，接著再進行下一次 epoch。） > 警告：隨機初始化隱藏層的連接權重是很重要的。假如所有的權重和偏置都初始化為 0，則在給定一層的所有神經元都是一樣的，BP 算法對這些神經元的調整也會是一樣的。換句話，就算每層有幾百個神經元，模型的整體表現就像每層只有一個神經元一樣，模型會顯得笨笨的。如果權重是隨機初始化的，就可以打破對稱性，訓練出不同的神經元。 為了使 BP 算法正常工作，作者對 MLP 的架構做了一個關鍵調整：用 Logistic 函數（sigmoid）代替階躍函數，`σ(z) = 1 / (1 + exp(–z))`。這是必要的，因為階躍函數只包含平坦的段，因此沒有梯度（梯度下降不能在平面上移動），而 Logistic 函數處處都有一個定義良好的非零導數，允許梯度下降在每步上取得一些進展。反向傳播算法也可以與其他激活函數一起使用，下面就是兩個流行的激活函數： * 雙曲正切函數： `tanh (z) = 2σ(2z) – 1` 類似 Logistic 函數，它是 S 形、連續可微的，但是它的輸出值范圍從-1 到 1（不是 Logistic 函數的 0 到 1），這往往使每層的輸出在訓練開始時或多或少都變得以 0 為中心，這常常有助于加快收斂速度。 * ReLU 函數：`ReLU(z) = max(0, z)` ReLU 函數是連續的，但是在`z=0`時不可微（斜率突然改變，導致梯度下降在 0 點左右跳躍），ReLU 的變體是當 z<0 時，z=0。但在實踐中，ReLU 效果很好，并且具有計算快速的優點，于是成為了默認激活函數。最重要的是，它沒有最大輸出值，這有助于減少梯度下降期間的一些問題（第 11 章再介紹）。 這些流行的激活函數及其變體如圖 10-8 所示。但是，究竟為什么需要激活函數呢？如果將幾個線性變化鏈式組合起來，得到的還是線性變換。比如，對于 `f(x) = 2x + 3` 和 `g(x) = 5x – 1` ，兩者組合起來仍是線性變換：`f(g(x)) = 2(5x – 1) + 3 = 10x + 1`。如果層之間不具有非線性，則深層網絡和單層網絡其實是等同的，這樣就不能解決復雜問題。相反的，足夠深且有非線性激活函數的 DNN，在理論上可以近似于任意連續函數。 圖 10-8 激活函數及其變體 知道了神經網絡的起源、架構、計算方法、BP 算法，接下來看應用。 ## 回歸 MLP 首先，MLP 可以用來回歸任務。如果想要預測一個單值（例如根據許多特征預測房價），就只需要一個輸出神經元，它的輸出值就是預測值。對于多變量回歸（即一次預測多個值），則每一維度都要有一個神經元。例如，想要定位一張圖片的中心，就要預測 2D 坐標，因此需要兩個輸出神經元。如果再給對象加個邊框，還需要兩個值：對象的寬度和高度。 通常，當用 MLP 做回歸時，輸出神經元不需要任何激活函數。如果要讓輸出是正值，則可在輸出值使用 ReLU 激活函數。另外，還可以使用 softplus 激活函數，這是 ReLu 的一個平滑化變體：`softplus(z) = log(1 + exp(z))`。z 是負值時，softplus 接近 0，z 是正值時，softplus 接近 z。最后，如果想讓輸出落入一定范圍內，則可以使用調整過的 Logistic 或雙曲正切函數：Logistic 函數用于 0 到 1，雙曲正切函數用于-1 到 1。 訓練中的損失函數一般是均方誤差，但如果訓練集有許多異常值，則可以使用平均絕對誤差。另外，也可以使用 Huber 損失函數，它是前兩者的組合。 > 提示：當誤差小于閾值δ時（一般為 1），Huber 損失函數是二次的；誤差大于閾值時，Huber 損失函數是線性的。相比均方誤差，線性部分可以讓 Huber 對異常值不那么敏感，二次部分可以讓收斂更快，也比均絕對誤差更精確。 表 10-1 總結了回歸 MLP 的典型架構。 表 10-1 回歸 MLP 的典型架構 ## 分類 MLP MLP 也可用于分類，對于二元分類問題，只需要一個使用 Logistic 激活的輸出神經元：輸出是一個 0 和 1 之間的值，作為正類的估計概率。 MLP 也可以處理多標簽二元分類（見第 3 章）。例如，郵件分類系統可以預測一封郵件是垃圾郵件，還是正常郵件，同時預測是緊急，還是非緊急郵件。這時，就需要兩個輸出神經元，兩個都是用 Logistic 函數：第一個輸出垃圾郵件的概率，第二個輸出緊急的概率。更為一般的講，需要為每個正類配一個輸出神經元。多個輸出概率的和不一定非要等于 1。這樣模型就可以輸出各種標簽的組合：非緊急非垃圾郵件、緊急非垃圾郵件、非緊急垃圾郵件、緊急垃圾郵件。 如果每個實例只能屬于一個類，但可能是三個或多個類中的一個（比如對于數字圖片分類，可以使 class 0 到 class 9），則每一類都要有一個輸出神經元，整個輸出層（見圖 10-9）要使用 softmax 激活函數。softmax 函數可以保證，每個估計概率位于 0 和 1 之間，并且各個值相加等于 1。這被稱為多類分類。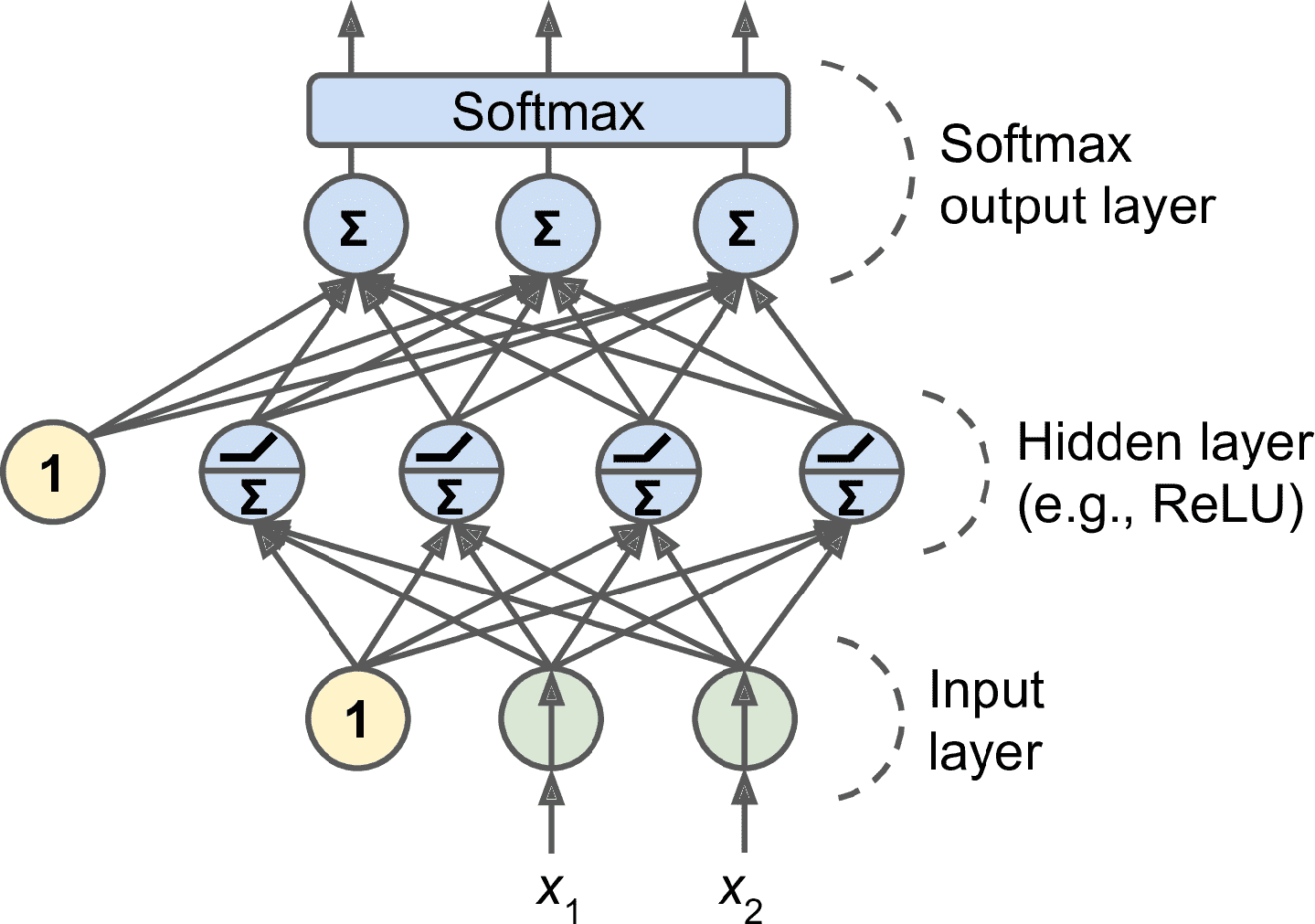 圖 10-9 一個用于分類的 MLP（包括 ReLU 和 softmax） 根據損失函數，因為要預測概率分布，交叉商損失函數（也稱為 log 損失，見第 4 章）是不錯的選擇。 表 10-2 概括了分類 MLP 的典型架構。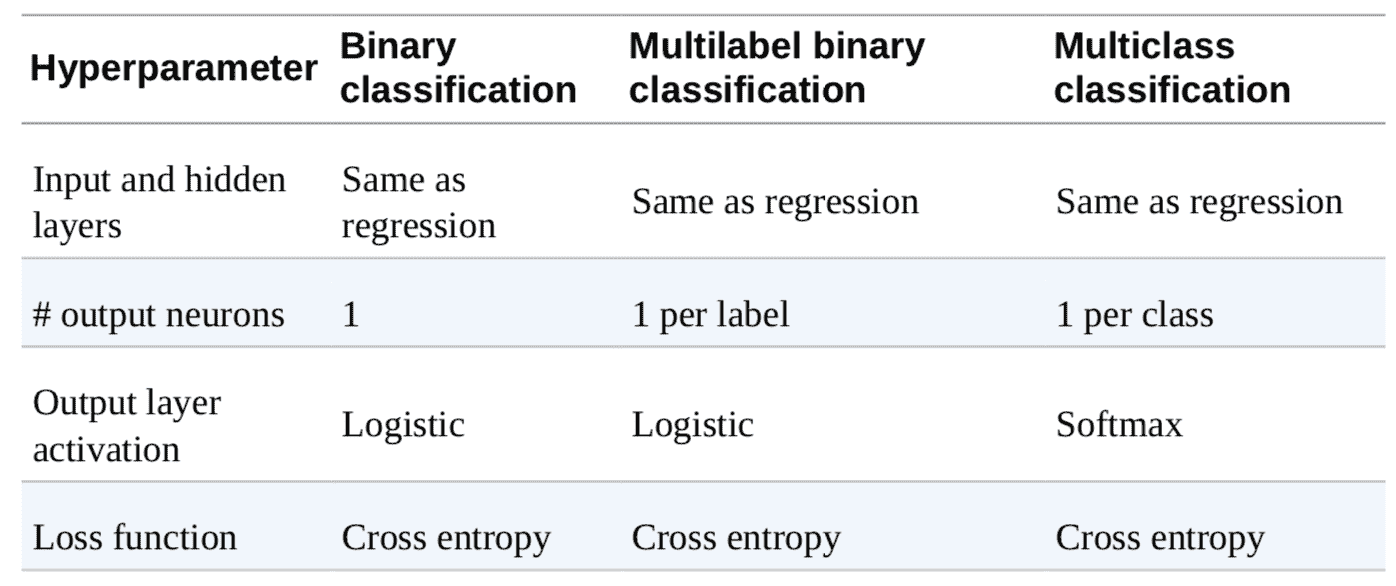 表 10-2 分類 MLP 的典型架構 > 提示：看下面的內容前，建議看看本章末尾的習題 1。利用 TensorFlow Playground 可視化各樣的神經網絡架構，可以更深入的理解 MLP 和超參數（層數、神經元數、激活函數）的作用。 # 用 Keras 實現 MLP Keras 是一個深度學習高級 API，可以用它輕松地搭建、訓練、評估和運行各種神經網絡。Keras 的文檔見[https://keras.io/](https://links.jianshu.com/go?to=https%3A%2F%2Fkeras.io%2F)。Keras 參考實現（[https://github.com/keras-team/keras](https://links.jianshu.com/go?to=https%3A%2F%2Fgithub.com%2Fkeras-team%2Fkeras)）是 Fran?ois Chollet 開發的，于 2015 年 3 月開源。得益于 Keras 簡單易用靈活優美，迅速流行開來。為了進行神經網絡計算，必須要有計算后端的支持。目前可選三個流行庫：TensorFlow、CNTK 和 Theano。為避免誤會，將 GitHub 上的 Keras 參考實現稱為多后端 Keras。 自從 2016 年底，出現了 Kera 的其它實現。現在已經可以在 Apache MXNet、蘋果 Core ML、JavaScript 或 TypeScript（瀏覽器）、PlaidML（各種 GPU，不限于 Nvidia）上運行 Keras。另外，TensorFlow 也捆綁了自身的 Keras 實現 —— tf.keras，它只支持 TensorFlow 作為后端，但提供了更多使用的功能（見圖 10-10）：例如，tf.keras 支持 TensorFlow 的 Data API，加載數據更輕松，預處理數據更高效。因此，本書使用的是 tf.keras。本章的代碼不局限于 TensorFlow，只需要一些修改，比如修改引入，也可以在其他 Keras 實現上運行。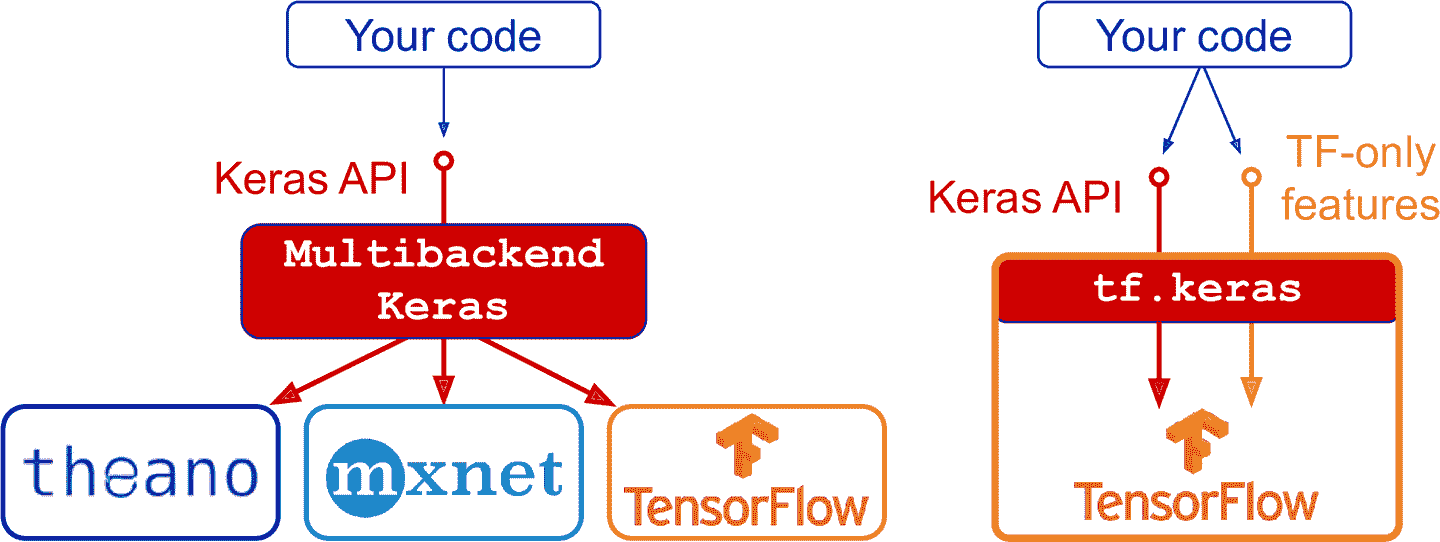 圖 10-10 Keras API 的兩個實現：左邊是多后端 Keras，右邊是 tf.keras 排在 Keras 和 TensorFlow 之后最流行的深度學習庫，是 Facebook 的 PyTorch。PyTorch 的 API 與 Keras 很像，所以掌握了 Keras，切換到 PyTorch 也不難。得益于易用性和詳實的文檔（TensorFlow 1 的文檔比較一般），PyTorch 在 2018 年廣泛流行開來。但是，TensorFlow 2 和 PyTorch 一樣簡單易用，因為 TensorFlow 使用了 Keras 作為它的高級 API，并簡化清理了 TensorFlow 的其它 API。TensorFlow 的文檔也改觀了，容易檢索多了。相似的，PyTorch 的缺點（可移植性差，沒有計算圖分析）在 PyTorch 1.0 版本中也得到了優化。良性競爭可以使所有人獲益。*（作者這段講的真好！）* ## 安裝 TensorFlow 2 假設已經在第 2 章中安裝了 Jupyter 和 Scikit-Learn，使用 pip 安裝 TensorFlow。如果使用了 virtualenv，先要激活虛擬環境： ```py $ cd $ML_PATH # Your ML working directory (e.g., $HOME/ml) $ source my_env/bin/activate # on Linux or macOS $ .\my_env\Scripts\activate # on Windows ``` 然后安裝 TensorFlow 2（如果沒有使用虛擬環境，需要管理員權限，或加上選項`--user`）: ```py $ python3 -m pip install --upgrade tensorflow ``` > 筆記：要使用 GPU 的話，在動筆寫書的此刻，需要安裝`tensorflow-gpu`，而不是`tensorflow`。但是 TensorFlow 團隊正在開發一個既支持 CPU 也支持 GPU 的獨立的庫。要支持 GPU 的話，可能還要安裝更多的庫，參考[*https://tensorflow.org/install*](https://links.jianshu.com/go?to=https%3A%2F%2Ftensorflow.org%2Finstall)。第 19 章會深入介紹 GPU。 要測試安裝是否成功，可以在 Python 終端或 Jupyter notebook 中引入 TensorFlow 和 tf.keras，然后打印其版本號： ```py >>> import tensorflow as tf >>> from tensorflow import keras >>> tf.__version__ '2.0.0' >>> keras.__version__ '2.2.4-tf' ``` 第二個版本號的末尾帶有`-tf`，表明是 tf.keras 實現的 Keras API，還有一些 TensorFlow 的專有功能。 ## 使用 Sequential API 創建圖片分類器 首先加載數據集。這章用的數據集是 Fashion MNIST，它是 MNIST 一個替代品，格式與 MNIST 完全相同（70000 張灰度圖，每張的像素是 28 × 28，共有 10 類），圖的內容是流行物品，而不是數字，每類中的圖片更豐富，識圖的挑戰性比 MNIST 高得多。例如，線性模型可以在 MNIST 上達到 92%的準確率，但在 Fashion MNIST 上只有 83%的準確率。 ### 使用 Keras 加載數據集 Keras 提供一些實用的函數用來獲取和加載常見的數據集，包括 MNIST、Fashion MNIST 和第 2 章用過的加州房產數據集。加載 Fashion MNIST： ```py fashion_mnist = keras.datasets.fashion_mnist (X_train_full, y_train_full), (X_test, y_test) = fashion_mnist.load_data() ``` 當使用 Keras 加載 MNIST 或 Fashion MNIST 時，和 Scikit-Learn 加載數據的一個重要區別是，每張圖片是 28 × 28 的數組，而不是大小是 784 的 1D 數組。另外像素的強度是用整數（0 到 255）表示的，而不是浮點數（0.0 到 255.0）。看下訓練集的形狀和類型： ```py >>> X_train_full.shape (60000, 28, 28) >>> X_train_full.dtype dtype('uint8') ``` 該數據集已經分成了訓練集和測試集，但沒有驗證集。所以要建一個驗證集，另外，因為要用梯度下降訓練神經網絡，必須要對輸入特征進行縮放。簡單起見，通過除以 255.0 將強度范圍變為 0-1： ```py X_valid, X_train = X_train_full[:5000] / 255.0, X_train_full[5000:] / 255.0 y_valid, y_train = y_train_full[:5000], y_train_full[5000:] ``` 對于 MNIST，當標簽等于 5 時，表明圖片是手寫的數字 5。但對于 Fashion MNIST，需要分類名的列表： ```py class_names = ["T-shirt/top", "Trouser", "Pullover", "Dress", "Coat", "Sandal", "Shirt", "Sneaker", "Bag", "Ankle boot"] ``` 例如，訓練集的第一張圖片表示外套： ```py >>> class_names[y_train[0]] 'Coat' ``` 圖 10-11 展示了 Fashion MNIST 數據集的一些樣本。 圖 10-11 Fashion MNIST 數據集的一些樣本 ### 用 Sequential API 創建模型 搭建一個擁有兩個隱含層的分類 MLP： ```py model = keras.models.Sequential() model.add(keras.layers.Flatten(input_shape=[28, 28])) model.add(keras.layers.Dense(300, activation="relu")) model.add(keras.layers.Dense(100, activation="relu")) model.add(keras.layers.Dense(10, activation="softmax")) ``` 逐行看下代碼： * 第一行代碼創建了一個 Sequential 模型，這是 Keras 最簡單的模型，是由單層神經元順序連起來的，被稱為 Sequential API； * 接下來創建了第一層，這是一個`Flatten`層，它的作用是將每個輸入圖片轉變為 1D 數組：如果輸入數據是`X`，該層則計算`X.reshape(-1, 1)`。該層沒有任何參數，只是做一些簡單預處理。因為是模型的第一層，必須要指明`input_shape`，`input_shape`不包括批次大小，只是實例的形狀。另外，第一層也可以是`keras.layers.InputLayer`，設置`input_shape=[28,28]`; * 然后，添加了一個有 300 個神經元的緊密層，激活函數是 ReLU。每個緊密層只負責自身的權重矩陣，權重矩陣是神經元與輸入的所有連接權重。緊密層還要負責偏置項（每個神經元都有一個偏置項）矢量。當緊密層收到輸入數據時，就利用公式 10-2 進行計算； * 接著再添加第二個緊密層，激活函數仍然是 ReLU； * 最后，加上一個擁有 10 個神經元的輸出層（每有一個類就要有一個神經元），激活函數是 softmax（保證輸出的概率和等于 1，因為就只有這是個類，具有排他性）。 > 提示：設置`activation="relu"`，等同于`activation=keras.activations.relu`。`keras.activations`包中還有其它激活函數，完整列表見[*https://keras.io/activations/*](https://links.jianshu.com/go?to=https%3A%2F%2Fkeras.io%2Factivations%2F)。 除了一層一層加層，也可以傳遞一個層組成的列表： ```py model = keras.models.Sequential([ keras.layers.Flatten(input_shape=[28, 28]), keras.layers.Dense(300, activation="relu"), keras.layers.Dense(100, activation="relu"), keras.layers.Dense(10, activation="softmax") ]) ``` > #### 使用 KERAS.IO 的代碼實例 > > keras.io 上的代碼也可以用于 tf.keras，但是需要修改引入。例如，對于下面的代碼： > > ```py > from keras.layers import Dense > output_layer = Dense(10) > ``` > > 需要改成： > > ```py > from tensorflow.keras.layers import Dense > output_layer = Dense(10) > ``` > > 或使用完整路徑： > > ```py > from tensorflow import keras > output_layer = keras.layers.Dense(10) > ``` > > 這么寫就是麻煩點，但是我在本書中是采用的這種方法，因為不僅可以容易看出使用的是哪個包，還可以避免搞混標準類和自定義類。在生產環境中，我傾向于使用前種方式。還有人喜歡這樣引入，`tensorflow.keras import layers`，使用`layers.Dense(10)`。 模型的`summary()`方法可以展示所有層，包括每個層的名字（名字是自動生成的，除非建層時指定名字），輸出的形狀（`None`代表批次大小可以是任意值），和參數的數量。最后會輸出所有參數的數量，包括可訓練和不可訓練參數。這章只有可訓練參數（第 11 章可以看到不可訓練參數的例子）： ```py >>> model.summary() Model: "sequential" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= flatten (Flatten) (None, 784) 0 _________________________________________________________________ dense (Dense) (None, 300) 235500 _________________________________________________________________ dense_1 (Dense) (None, 100) 30100 _________________________________________________________________ dense_2 (Dense) (None, 10) 1010 ================================================================= Total params: 266,610 Trainable params: 266,610 Non-trainable params: 0 _________________________________________________________________ ``` 緊密層通常有許多參數。比如，第一個隱含層有 784 × 300 個連接權重，再加上 300 個偏置項，總共有 235500 個參數。這么多參數可以讓模型具有足夠的靈活度以擬合訓練數據，但也意味著可能有過擬合的風險，特別是當訓練數據不足時。后面再討論這個問題。 使用屬性，獲取神經層很容易，可以通過索引或名稱獲取對應的層： ```py >>> model.layers [<tensorflow.python.keras.layers.core.Flatten at 0x132414e48>, <tensorflow.python.keras.layers.core.Dense at 0x1324149b0>, <tensorflow.python.keras.layers.core.Dense at 0x1356ba8d0>, <tensorflow.python.keras.layers.core.Dense at 0x13240d240>] >>> hidden1 = model.layers[1] >>> hidden1.name 'dense' >>> model.get_layer('dense') is hidden1 True ``` 可以用`get_weights()`和`set_weights()`方法，獲取神經層的所有參數。對于緊密層，參數包括連接權重和偏置項： ```py >>> weights, biases = hidden1.get_weights() >>> weights array([[ 0.02448617, -0.00877795, -0.02189048, ..., -0.02766046, 0.03859074, -0.06889391], ..., [-0.06022581, 0.01577859, -0.02585464, ..., -0.00527829, 0.00272203, -0.06793761]], dtype=float32) >>> weights.shape (784, 300) >>> biases array([0., 0., 0., 0., 0., 0., 0., 0., 0., ..., 0., 0., 0.], dtype=float32) >>> biases.shape (300,) ``` 緊密層是隨機初始化連接權重的（為了避免對稱性），偏置項則是 0。如果想使用不同的初始化方法，可以在創建層時設置`kernel_initializer`（kernel 是連接矩陣的另一個名字）或`bias_initializer`。第 11 章會進一步討論初始化器，初始化器的完整列表見[*https://keras.io/initializers/*](https://links.jianshu.com/go?to=https%3A%2F%2Fkeras.io%2Finitializers%2F)。 > 筆記：權重矩陣的形狀取決于輸入的數量。這就是為什么要在創建`Sequential`模型的第一層時指定`input_shape`。但是，如果不指定形狀也沒關系：Keras 會在真正搭建模型前一直等待，直到弄清輸入的形狀（輸入真實數據時，或調用`build()`方法時）。在搭建模型之前，神經層是沒有權重的，也干不了什么事（比如打印模型概要或保存模型）。所以如果在創建模型時知道輸入的形狀，最好就設置好。 ### 編譯模型 創建好模型之后，必須調用`compile()`方法，設置損失函數和優化器。另外，還可以指定訓練和評估過程中要計算的額外指標的列表： ```py model.compile(loss="sparse_categorical_crossentropy", optimizer="sgd", metrics=["accuracy"]) ``` > 筆記：使用`loss="sparse_categorical_crossentropy"`等同于`loss=keras.losses.sparse_categorical_crossentropy`。相思的，`optimizer="sgd"`等同于`optimizer=keras.optimizers.SGD()`，`metrics=["accuracy"]`等同于`metrics=[keras.metrics.sparse_categorical_accuracy]`。后面還會使用其他的損失函數、優化器和指標，它們的完整列表見[*https://keras.io/losses*](https://links.jianshu.com/go?to=https%3A%2F%2Fkeras.io%2Flosses)、 [*https://keras.io/optimizers*](https://links.jianshu.com/go?to=https%3A%2F%2Fkeras.io%2Foptimizers)、和 [*https://keras.io/metrics*](https://links.jianshu.com/go?to=https%3A%2F%2Fkeras.io%2Fmetrics)。 解釋下這段代碼。首先，因為使用的是稀疏標簽（每個實例只有一個目標類的索引，在這個例子中，目標類索引是 0 到 9），且就是這十個類，沒有其它的，所以使用的是`"sparse_categorical_crossentropy"`損失函數。如果每個實例的每個類都有一個目標概率（比如獨熱矢量，`[0., 0., 0., 1., 0., 0., 0., 0., 0., 0.]`，來表示類 3），則就要使用`"categorical_crossentropy"`損失函數。如果是做二元分類（有一個或多個二元標簽），輸出層就得使用`"sigmoid"`激活函數，損失函數則變為`"binary_crossentropy"`。 > 提示：如果要將稀疏標簽轉變為獨熱矢量標簽，可以使用函數`keras.utils.to_categorical()`。還以使用函數`np.argmax()`，`axis=1`。 對于優化器，`"sgd"`表示使用隨機梯度下降訓練模型。換句話說，Keras 會進行反向傳播算法。第 11 章會討論更高效的優化器（可以提升梯度下降部分，改善不了自動微分部分）。 > 筆記：使用`SGD`時，調整學習率很重要，必須要手動設置好，`optimizer=keras.optimizers.SGD(lr=???)`。`optimizer="sgd"`不同，它的學習率默認為`lr=0.01`。 最后，因為是個分類器，最好在訓練和評估時測量`"accuracy"`。 ### 訓練和評估模型 可以訓練模型了。只需調用`fit()`方法： ```py >>> history = model.fit(X_train, y_train, epochs=30, ... validation_data=(X_valid, y_valid)) ... Train on 55000 samples, validate on 5000 samples Epoch 1/30 55000/55000 [======] - 3s 49us/sample - loss: 0.7218 - accuracy: 0.7660 - val_loss: 0.4973 - val_accuracy: 0.8366 Epoch 2/30 55000/55000 [======] - 2s 45us/sample - loss: 0.4840 - accuracy: 0.8327 - val_loss: 0.4456 - val_accuracy: 0.8480 [...] Epoch 30/30 55000/55000 [======] - 3s 53us/sample - loss: 0.2252 - accuracy: 0.9192 - val_loss: 0.2999 - val_accuracy: 0.8926 ``` 這里，向`fit()`方法傳遞了輸入特征`(X_train)`和目標類`(y_train)`，還要要訓練的周期數（不設置的話，默認的周期數是 1，肯定是不能收斂到一個好的解的）。另外還傳遞了驗證集（它是可選的）。Keras 會在每個周期結束后，測量損失和指標，這樣就可以監測模型的表現。如果模型在訓練集上的表現優于在驗證集上的表現，可能模型在訓練集上就過擬合了（或者就是存在 bug，比如訓練集和驗證集的數據不匹配）。 僅需如此，神經網絡就訓練好了。訓練中的每個周期，Keras 會展示到目前為止一共處理了多少個實例（還帶有進度條），每個樣本的平均訓練時間，以及在訓練集和驗證集上的損失和準確率（和其它指標）。可以看到，損失是一直下降的，這是一個好現象。經過 30 個周期，驗證集的準確率達到了 89.26%，與在訓練集上的準確率差不多，所以沒有過擬合。 > 提示：除了通過參數`validation_data`傳遞驗證集，也可以通過參數`validation_split`從訓練集分割出一部分作為驗證集。比如，`validation_split=0.1`可以讓 Keras 使用訓練數據（打散前）的末尾 10%作為驗證集。 如果訓練集非常傾斜，一些類過渡表達，一些欠表達，在調用`fit()`時最好設置`class_weight`參數，可以加大欠表達類的權重，減小過渡表達類的權重。Keras 在計算損失時，會使用這些權重。如果每個實例都要加權重，可以設置`sample_weight`（這個參數優先于`class_weight`）。如果一些實例的標簽是通過專家添加的，其它實例是通過眾包平臺添加的，最好加大前者的權重，此時給每個實例都加權重就很有必要。通過在`validation_data`元組中，給驗證集加上樣本權重作為第三項，還可以給驗證集添加樣本權重。 `fit()`方法會返回`History`對象，包含：訓練參數（`history.params`）、周期列表（history.epoch）、以及最重要的包含訓練集和驗證集的每個周期后的損失和指標的字典（`history.history`）。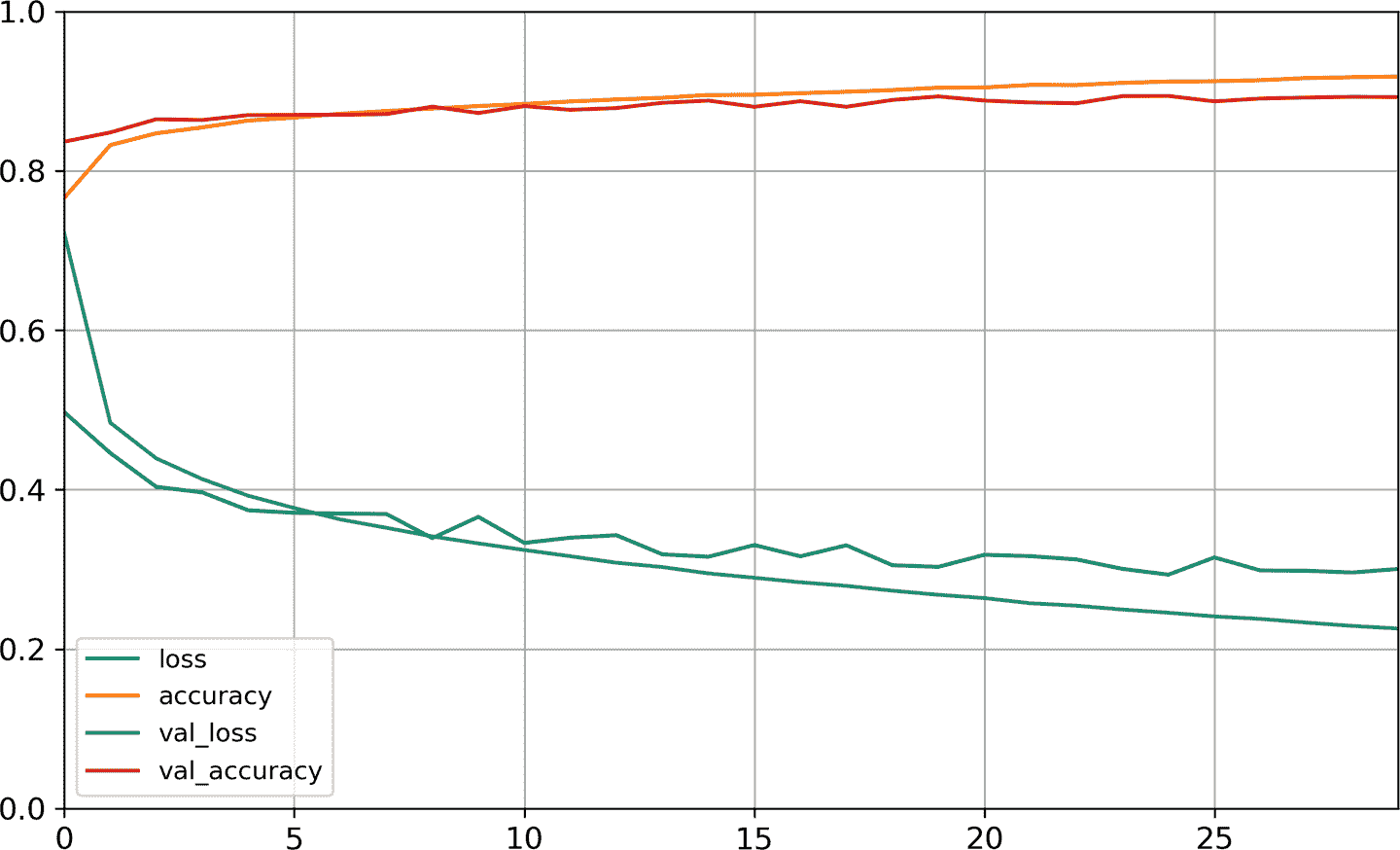如果用這個字典創建一個 pandas 的 DataFrame，然后使用方法`plot()`，就可以畫出學習曲線，見圖 10-12： ```py import pandas as pd import matplotlib.pyplot as plt pd.DataFrame(history.history).plot(figsize=(8, 5)) plt.grid(True) plt.gca().set_ylim(0, 1) # set the vertical range to [0-1] plt.show() ``` 圖 10-12 學習曲線：每個周期的平均訓練損失和準確率，驗證損失和準確率 可以看到，訓練準確率和驗證準確率穩步提高，訓練損失和驗證損失持續下降。另外，驗證曲線和訓練曲線靠的很近，意味著沒有什么過擬合。在這個例子中，在訓練一開始時，模型在驗證集上的表現由于訓練集。但實際情況是，驗證誤差是在每個周期結束后算出來的，而訓練誤差在每個周期期間，用流動平均誤差算出來的。所以訓練曲線（譯者注，圖中橙色的那條）實際應該向左移動半個周期。移動之后，就可以發現在訓練開始時，訓練和驗證曲線幾乎是完美重合起來的。 > 提示：在繪制訓練曲線時，應該向左移動半個周期。 通常只要訓練時間足夠長，訓練集的表現就能超越驗證集。從圖中可以看到，驗證損失仍然在下降，模型收斂的還不好，所以訓練應該持續下去。只需要再次調用方法`fit()`即可，因為 Keras 可以從斷點處繼續（驗證準確率可以達到 89%。） 如果仍然對模型的表現不滿意，就需要調節超參數了。首先是學習率。如果調節學習率沒有幫助，就嘗試換一個優化器（記得再調節任何超參數之后都重新調節學習率）。如果效果仍然不好，就調節模型自身的超參數，比如層數、每層的神經元數，每個隱藏層的激活函數。還可以調節其它超參數，比如批次大小（通過`fit()`的參數`batch_size`，默認是 32）。本章末尾還會調節超參數。當對驗證準確率達到滿意之后，就可以用測試集評估泛化誤差。只需使用`evaluate()`方法（`evaluate()`方法包含參數`batch_size`和`sample_weight`）： ```py >>> model.evaluate(X_test, y_test) 10000/10000 [==========] - 0s 29us/sample - loss: 0.3340 - accuracy: 0.8851 [0.3339798209667206, 0.8851] ``` 正如第 2 章所見，測試集的表現通常比驗證集上低一點，這是因為超參數根據驗證集而不是測試集調節的（但是在這個例子中，我們沒有調節過超參數，所以準確率下降純粹是運氣比較差而已）。一定不要在測試集上調節超參數，否則會影響泛化誤差。 ### 使用模型進行預測 接下來，就可以用模型的`predict()`方法對新實例做預測了。因為并沒有新實例，所以就用測試集的前 3 個實例來演示： ```py >>> X_new = X_test[:3] >>> y_proba = model.predict(X_new) >>> y_proba.round(2) array([[0\. , 0\. , 0\. , 0\. , 0\. , 0.03, 0\. , 0.01, 0\. , 0.96], [0\. , 0\. , 0.98, 0\. , 0.02, 0\. , 0\. , 0\. , 0\. , 0\. ], [0\. , 1\. , 0\. , 0\. , 0\. , 0\. , 0\. , 0\. , 0\. , 0\. ]], dtype=float32) ``` 可以看到，模型會對每個實例的每個類（從 0 到 9）都給出一個概率。比如，對于第一張圖，模型預測第 9 類（短靴）的概率是 96%，第 5 類（涼鞋）的概率是 3%，第 7 類（運動鞋）的概率是 1%，剩下的類的概率都是 0。換句話說，模型預測第一張圖是鞋，最有可能是短靴，也有可能是涼鞋和運動鞋。如果只關心概率最高的類（即使概率不高），可以使用方法`predict_classes()`： ```py >>> y_pred = model.predict_classes(X_new) >>> y_pred array([9, 2, 1]) >>> np.array(class_names)[y_pred] array(['Ankle boot', 'Pullover', 'Trouser'], dtype='<U11') ``` 對于這 3 個實例，模型的判斷都是對的（見圖 10-13）： ```py >>> y_new = y_test[:3] >>> y_new array([9, 2, 1]) ``` 圖 10-13 正確分類的 Fashion MNIST 圖片 到此為止，我們學會了如何使用 Sequential API 來搭建、訓練、評估和使用分類 MLP？如何來做回歸呢？ ## 使用 Sequential API 搭建回歸 MLP 接下來使用回歸神經網絡來處理加州房價問題。簡便起見，使用 Scikit-Learn 的`fetch_california_housing()`函數來加載數據。這個數據集比第 2 章所用的數據集簡單，因為它只包括數值特征（沒有`ocean_proximity`），也不包括缺失值。加載好數據之后，將數據集分割成訓練集、驗證集和測試集，并做特征縮放： ```py from sklearn.datasets import fetch_california_housing from sklearn.model_selection import train_test_split from sklearn.preprocessing import StandardScaler housing = fetch_california_housing() X_train_full, X_test, y_train_full, y_test = train_test_split( housing.data, housing.target) X_train, X_valid, y_train, y_valid = train_test_split( X_train_full, y_train_full) scaler = StandardScaler() X_train = scaler.fit_transform(X_train) X_valid = scaler.transform(X_valid) X_test = scaler.transform(X_test) ``` 使用 Sequential API 搭建、訓練、評估和使用回歸 MLP 做預測，和前面的分類 MLP 很像。區別在于輸出層只有一個神經元（因為只想預測一個值而已），也沒有使用激活函數，損失函數是均方誤差。因為數據集有噪音，我們就是用一個隱藏層，并且神經元也比之前少，以避免過擬合： ```py model = keras.models.Sequential([ keras.layers.Dense(30, activation="relu", input_shape=X_train.shape[1:]), keras.layers.Dense(1) ]) model.compile(loss="mean_squared_error", optimizer="sgd") history = model.fit(X_train, y_train, epochs=20, validation_data=(X_valid, y_valid)) mse_test = model.evaluate(X_test, y_test) X_new = X_test[:3] # pretend these are new instances y_pred = model.predict(X_new) ``` 可以看到，使用 Sequential API 是很方便的。但是，盡管`Sequential`十分常見，但用它搭建復雜拓撲形態或多輸入多輸出的神經網絡還是不多。所以，Keras 還提供了 Functional API。 ## 使用 Functional API 搭建復雜模型 Wide & Deep 是一個非序列化的神經網絡模型。這個架構是 Heng-Tze Cheng 在 2016 年在論文（[https://arxiv.org/abs/1606.07792](https://links.jianshu.com/go?to=https%3A%2F%2Farxiv.org%2Fabs%2F1606.07792)）中提出來的。這個模型可以將全部或部分輸入與輸出層連起來，見圖 10-14。這樣，就可以既學到深層模式（使用深度路徑）和簡單規則（使用短路徑）。作為對比，常規 MLP 會強制所有數據流經所有層，因此數據中的簡單模式在多次變換后會被扭曲。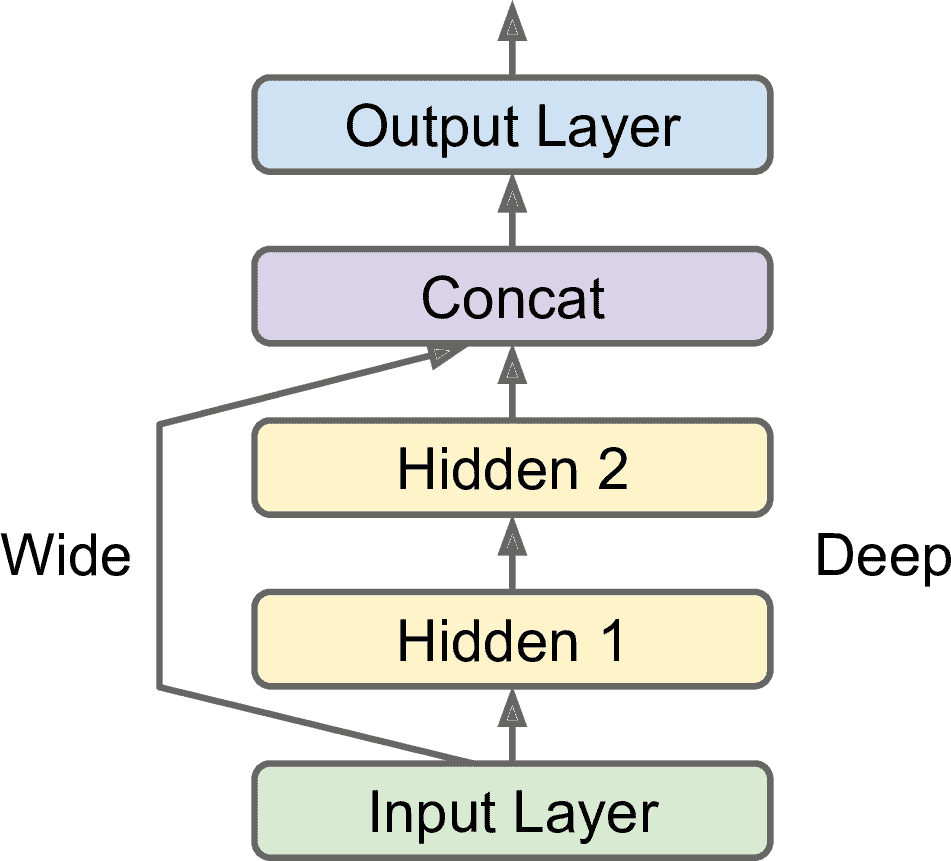 圖 10-14 Wide & Deep 神經網絡 我們來搭建一個這樣的神經網絡，來解決加州房價問題： ```py input_ = keras.layers.Input(shape=X_train.shape[1:]) hidden1 = keras.layers.Dense(30, activation="relu")(input_) hidden2 = keras.layers.Dense(30, activation="relu")(hidden1) concat = keras.layers.Concatenate()([input_, hidden2]) output = keras.layers.Dense(1)(concat) model = keras.Model(inputs=[input_], outputs=[output]) ``` 每行代碼的作用： * 首先創建一個`Input`對象。包括模型輸入的形狀`shape`和數據類型`dtype`。模型可能會有多種輸入。 * 然后，創建一個有 30 個神經元的緊密層，激活函數是 ReLU。創建好之后，將其作為函數，直接將輸入傳給它。這就是 Functional API 的得名原因。這里只是告訴 Keras 如何將層連起來，并沒有導入實際數據。 * 然后創建第二個隱藏層，還是將其作為函數使用，輸入時第一個隱藏層的輸出； * 接著，創建一個連接`Concatenate`層，也是作為函數使用，將輸入和第二個隱藏層的輸出連起來。可以使用`keras.layers.concatenate()`。 * 然后創建輸出層，只有一個神經元，沒有激活函數，將連接層的輸出作為輸入。 * 最后，創建一個 Keras 的`Model`，指明輸入和輸出。 搭建好模型之后，重復之前的步驟：編譯模型、訓練、評估、做預測。 但是如果你想將部分特征發送給 wide 路徑，將部分特征（可以有重疊）發送給 deep 路徑，該怎么做呢？答案是可以使用多輸入。例如，假設向 wide 路徑發送 5 個特征（特征 0 到 4），向 deep 路徑發送 6 個特征（特征 2 到 7）： 圖 10-15 處理多輸入 ```py input_A = keras.layers.Input(shape=[5], name="wide_input") input_B = keras.layers.Input(shape=[6], name="deep_input") hidden1 = keras.layers.Dense(30, activation="relu")(input_B) hidden2 = keras.layers.Dense(30, activation="relu")(hidden1) concat = keras.layers.concatenate([input_A, hidden2]) output = keras.layers.Dense(1, name="output")(concat) model = keras.Model(inputs=[input_A, input_B], outputs=[output]) ``` 代碼非常淺顯易懂。值得注意的是，在創建模型時，我們指明了`inputs=[input_A, input_B]`。然后就可以像通常那樣編譯模型了，但當調用`fit()`時，不是傳入矩陣`X_train`，而是傳入一對矩陣`(X_train_A, X_train_B)`：每個輸入一個矩陣。同理調用`evaluate()`或`predict()`時，`X_valid`、`X_test`、`X_new`也要變化： ```py model.compile(loss="mse", optimizer=keras.optimizers.SGD(lr=1e-3)) X_train_A, X_train_B = X_train[:, :5], X_train[:, 2:] X_valid_A, X_valid_B = X_valid[:, :5], X_valid[:, 2:] X_test_A, X_test_B = X_test[:, :5], X_test[:, 2:] X_new_A, X_new_B = X_test_A[:3], X_test_B[:3] history = model.fit((X_train_A, X_train_B), y_train, epochs=20, validation_data=((X_valid_A, X_valid_B), y_valid)) mse_test = model.evaluate((X_test_A, X_test_B), y_test) y_pred = model.predict((X_new_A, X_new_B)) ``` 有以下要使用多輸入的場景： * 任務要求。例如，你想定位和分類圖片中的主要物體。這既是一個回歸任務（找到目標中心的坐標、寬度和高度）和分類任務。 * 相似的，對于相同的數據，你可能有多個獨立的任務。當然可以每個任務訓練一個神經網絡，但在多數情況下，同時對所有任務訓練一個神經網絡，每個任務一個輸出，后者的效果更好。這是因為神經網絡可以在不同任務間學習有用的數據特征。例如，在人臉的多任務分類時，你可以用一個輸出做人物表情的分類（微笑驚訝等等），用另一個輸出判斷是否戴著眼鏡。 * 另一種情況是作為一種正則的方法（即，一種降低過擬合和提高泛化能力的訓練約束）。例如，你想在神經網絡中加入一些輔助輸出（見圖 10-16），好讓神經網絡的一部分依靠自身就能學到一些東西。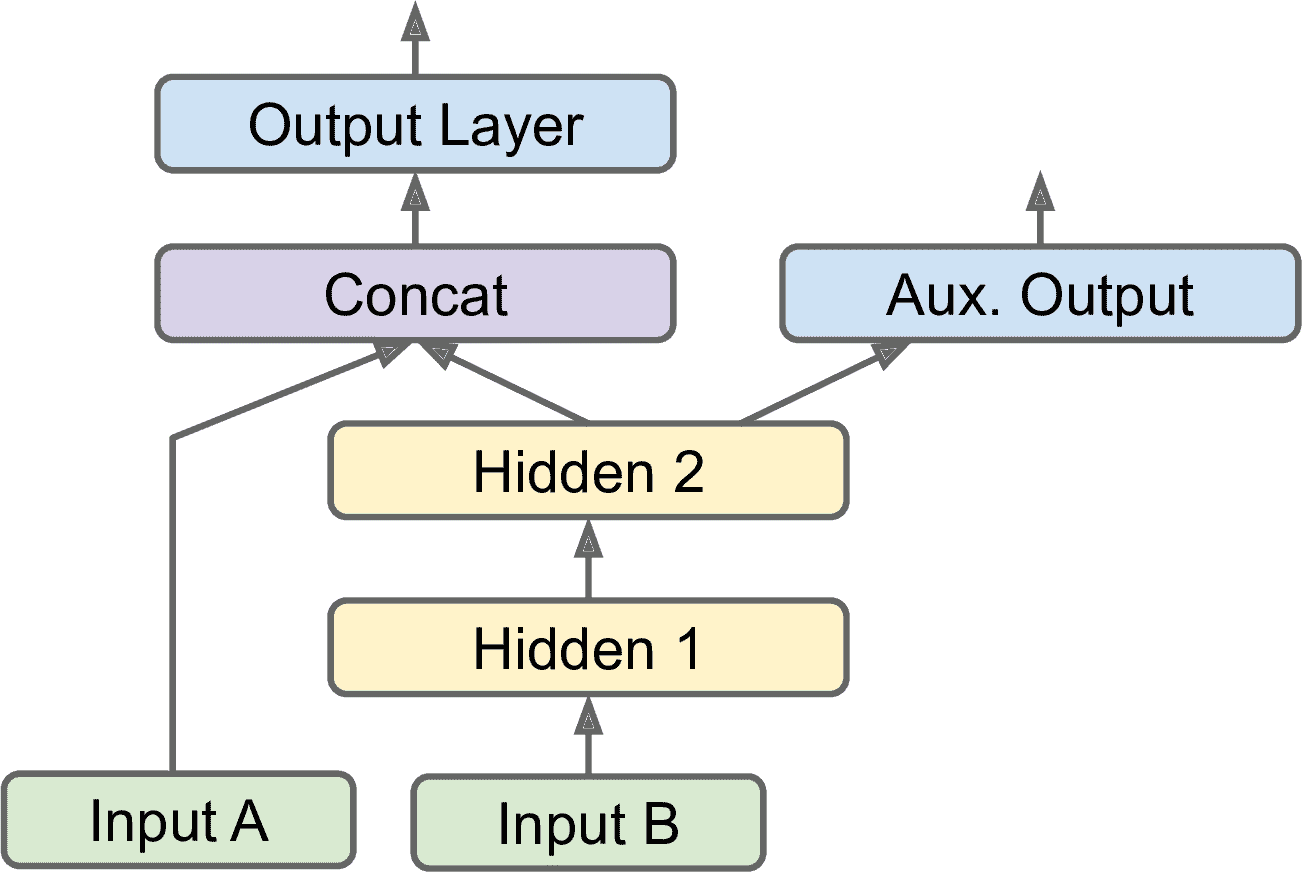 圖 10-16 處理多輸入，加入輔助輸出作為正則 添加額外的輸出很容易：只需要將輸出和相關的層連起來、將輸出寫入輸出列表就行。例如，下面的代碼搭建的就是圖 10-16 的架構： ```py [...] # output 層前面都一樣 output = keras.layers.Dense(1, name="main_output")(concat) aux_output = keras.layers.Dense(1, name="aux_output")(hidden2) model = keras.Model(inputs=[input_A, input_B], outputs=[output, aux_output]) ``` 每個輸出都要有自己的損失函數。因此在編譯模型時，需要傳入損失列表（如果只傳入一個損失，Keras 會認為所有輸出是同一個損失函數）。Keras 默認計算所有損失，將其求和得到最終損失用于訓練。主輸出比輔助輸出更值得關心，所以要提高它的權重，如下所示： ```py model.compile(loss=["mse", "mse"], loss_weights=[0.9, 0.1], optimizer="sgd") ``` 此時若要訓練模型，必須給每個輸出貼上標簽。在這個例子中，主輸出和輔輸出預測的是同一件事，因此標簽相同。傳入數據必須是`(y_train, y_train)`（`y_valid`和`y_test`也是如此）： ```py history = model.fit( [X_train_A, X_train_B], [y_train, y_train], epochs=20, validation_data=([X_valid_A, X_valid_B], [y_valid, y_valid])) ``` 當評估模型時，Keras 會返回總損失和各個損失值： ```py total_loss, main_loss, aux_loss = model.evaluate( [X_test_A, X_test_B], [y_test, y_test]) ``` 相似的，方法`predict()`會返回每個輸出的預測值： ```py y_pred_main, y_pred_aux = model.predict([X_new_A, X_new_B]) ``` 可以看到，用 Functional API 可以輕易搭建任意架構。接下來再看最后一種搭建 Keras 模型的方法。 ## 使用 Subclassing API 搭建動態模型 Sequential API 和 Functional API 都是聲明式的：只有聲明創建每個層以及層的連接方式，才能給模型加載數據以進行訓練和推斷。這種方式有其優點：模型可以方便的進行保存、克隆和分享；模型架構得以展示，便于分析；框架可以推斷數據形狀和類型，便于及時發現錯誤（加載數據之前就能發現錯誤）。調試也很容易，因為模型是層的靜態圖。但是缺點也很明顯：模型是靜態的。一些模型包含循環、可變數據形狀、條件分支，和其它的動態特點。對于這些情況，或者你只是喜歡命令式編程，不妨使用 Subclassing API。 對`Model`類劃分子類，在構造器中創建需要的層，調用`call()`進行計算。例如，創建一個下面的`WideAndDeepModel`類的實例，就可以創建與前面 Functional API 例子的同樣模型，同樣可以進行編譯、評估、預測： ```py class WideAndDeepModel(keras.Model): def __init__(self, units=30, activation="relu", **kwargs): super().__init__(**kwargs) # handles standard args (e.g., name) self.hidden1 = keras.layers.Dense(units, activation=activation) self.hidden2 = keras.layers.Dense(units, activation=activation) self.main_output = keras.layers.Dense(1) self.aux_output = keras.layers.Dense(1) def call(self, inputs): input_A, input_B = inputs hidden1 = self.hidden1(input_B) hidden2 = self.hidden2(hidden1) concat = keras.layers.concatenate([input_A, hidden2]) main_output = self.main_output(concat) aux_output = self.aux_output(hidden2) return main_output, aux_output model = WideAndDeepModel() ``` 這個例子和 Functional API 很像，除了不用創建輸入；只需要在`call()`使用參數`input`，另外的不同是將層的創建和和使用分割了。最大的差別是，在`call()`方法中，你可以做任意想做的事：for 循環、if 語句、低級的 TensorFlow 操作，可以盡情發揮想象（見第 12 章）！Subclassing API 可以讓研究者試驗各種新創意。 然而代價也是有的：模型架構隱藏在`call()`方法中，所以 Keras 不能對其檢查；不能保存或克隆；當調用`summary()`時，得到的只是層的列表，沒有層的連接信息。另外，Keras 不能提前檢查數據類型和形狀，所以很容易犯錯。所以除非真的需要靈活性，還是使用 Sequential API 或 Functional API 吧。 > 提示：可以像常規層一樣使用 Keras 模型，組合模型搭建任意復雜的架構。 學會了搭建和訓練神經網絡，接下來看看如何保存。 ## 保存和恢復模型 使用 Sequential API 或 Functional API 時，保存訓練好的 Keras 模型和訓練一樣簡單： ```py model = keras.layers.Sequential([...]) # or keras.Model([...]) model.compile([...]) model.fit([...]) model.save("my_keras_model.h5") ``` Keras 使用 HDF5 格式保存模型架構（包括每層的超參數）和每層的所有參數值（連接權重和偏置項）。還保存了優化器（包括超參數和狀態）。 通常用腳本訓練和保存模型，一個或更多的腳本（或 web 服務）來加載模型和做預測。加載模型很簡單： ```py model = keras.models.load_model("my_keras_model.h5") ``` > 警告：這種加載模型的方法只對 Sequential API 或 Functional API 有用，不適用于 Subclassing API。對于后者，可以用`save_weights()`和`load_weights()`保存參數，其它的就得手動保存恢復了。 但如果訓練要持續數個小時呢？在大數據集上訓練，訓練時間長很普遍。此時，不僅要在訓練結束時保存模型檢查點，在一定時間間隔內也要保存，以免電腦宕機造成損失。但是如何告訴`fit()`保存檢查點呢？使用調回。 ### 使用調回 `fit()`方法接受參數`callbacks`，可以讓用戶指明一個 Keras 列表，讓 Keras 在訓練開始和結束、每個周期開始和結束、甚至是每個批次的前后調用。例如，`ModelCheckpoint`可以在每個時間間隔保存檢查點，默認是每個周期結束之后： ```py [...] # 搭建編譯模型 checkpoint_cb = keras.callbacks.ModelCheckpoint("my_keras_model.h5") history = model.fit(X_train, y_train, epochs=10, callbacks=[checkpoint_cb]) ``` 另外，如果訓練時使用了驗證集，可以在創建檢查點時設定`save_best_only=True`，只有當模型在驗證集上取得最優值時才保存模型。這么做可以不必擔心訓練時間過長和訓練集過擬合：只需加載訓練好的模型，就能保證是在驗證集上表現最好的模型。下面的代碼演示了早停（見第 4 章）： ```py checkpoint_cb = keras.callbacks.ModelCheckpoint("my_keras_model.h5", save_best_only=True) history = model.fit(X_train, y_train, epochs=10, validation_data=(X_valid, y_valid), callbacks=[checkpoint_cb]) model = keras.models.load_model("my_keras_model.h5") # roll back to best model ``` 另一種實現早停的方法是使用`EarlyStopping`調回。當檢測到經過幾個周期（周期數由參數`patience`確定），驗證集表現沒有提升時，就會中斷訓練，還能自動滾回到最優模型。可以將保存檢查點（避免宕機）和早停（避免浪費時間和資源）結合起來： ```py early_stopping_cb = keras.callbacks.EarlyStopping(patience=10, restore_best_weights=True) history = model.fit(X_train, y_train, epochs=100, validation_data=(X_valid, y_valid), callbacks=[checkpoint_cb, early_stopping_cb]) ``` 周期數可以設的很大，因為準確率沒有提升時，訓練就會自動停止。此時，就沒有必要恢復最優模型，因為`EarlyStopping`調回一直在跟蹤最優權重，訓練結束時能自動恢復。 > 提示：包[`keras.callbacks`](https://links.jianshu.com/go?to=https%3A%2F%2Fkeras.io%2Fcallbacks%2F)中還有其它可用的調回。 如果還想有其它操控，還可以編寫自定義的調回。下面的例子展示了一個可以展示驗證集損失和訓練集損失比例的自定義（檢測過擬合）調回： ```py class PrintValTrainRatioCallback(keras.callbacks.Callback): def on_epoch_end(self, epoch, logs): print("\nval/train: {:.2f}".format(logs["val_loss"] / logs["loss"])) ``` 類似的，還可以實現`on_train_begin()`、`on_train_end()`、`on_epoch_begin()`、`on_epoch_end()`、`on_batch_begin()`、和`on_batch_end()`。如果需要的話，在評估和預測時也可以使用調回（例如為了調試）。對于評估，可以實現`on_test_begin()`、`on_test_end()`、`on_test_batch_begin()`或`on_test_batch_end()`（通過`evaluate()`調用）；對于預測，可以實現`on_predict_begin()`、`on_predict_end()`、`on_predict_batch_begin()`或`on_predict_batch_end()`（通過`predict()`調用）。 下面來看一個使用`tf.keras`的必備工具：TensorBoard。 ### 使用 TensorBoard 進行可視化 TensorBoard 是一個強大的交互可視化工具，使用它可以查看訓練過程中的學習曲線、比較每次運行的學習曲線、可視化計算圖、分析訓練數據、查看模型生成的圖片、可視化投射到 3D 的多維數據，等等。TensorBoard 是 TensorFlow 自帶的。 要使用 TensorBoard，必須修改程序，將要可視化的數據輸出為二進制的日志文件`event files`。每份二進制數據稱為摘要`summary`，TensorBoard 服務器會監測日志文件目錄，自動加載更新并可視化：這樣就能看到實時數據（稍有延遲），比如訓練時的學習曲線。通常，將 TensorBoard 服務器指向根日志目錄，程序的日志寫入到它的子目錄，這樣一個 TensorBoard 服務就能可視化并比較多次運行的數據，而不會將其搞混。 我們先定義 TensorBoard 的根日志目錄，還有一些根據當前日期生成子目錄的小函數。你可能還想在目錄名中加上其它信息，比如超參數的值，方便知道查詢的內容： ```py import os root_logdir = os.path.join(os.curdir, "my_logs") def get_run_logdir(): import time run_id = time.strftime("run_%Y_%m_%d-%H_%M_%S") return os.path.join(root_logdir, run_id) run_logdir = get_run_logdir() # e.g., './my_logs/run_2019_06_07-15_15_22' ``` Keras 提供了一個`TensorBoard()`調回： ```py [...] # 搭建編譯模型 tensorboard_cb = keras.callbacks.TensorBoard(run_logdir) history = model.fit(X_train, y_train, epochs=30, validation_data=(X_valid, y_valid), callbacks=[tensorboard_cb]) ``` 簡直不能再簡單了。如果運行這段代碼，`TensorBoard()`調回會負責創建日志目錄（包括父級目錄），在訓練過程中會創建事件文件并寫入概要。再次運行程序（可能修改了一些超參數）之后，得到的目錄結構可能如下： ```py my_logs/ ├── run_2019_06_07-15_15_22 │ ├── train │ │ ├── events.out.tfevents.1559891732.mycomputer.local.38511.694049.v2 │ │ ├── events.out.tfevents.1559891732.mycomputer.local.profile-empty │ │ └── plugins/profile/2019-06-07_15-15-32 │ │ └── local.trace │ └── validation │ └── events.out.tfevents.1559891733.mycomputer.local.38511.696430.v2 └── run_2019_06_07-15_15_49 └── [...] ``` 每次運行都會創建一個目錄，每個目錄都有一個包含訓練日志和驗證日志的子目錄。兩者都包括事件文件，訓練日志還包括分析追蹤信息：它可以讓 TensorBoard 展示所有設備上的模型的各個部分的訓練時長，有助于定位性能瓶頸。 然后就可以啟動 TensorBoard 服務了。一種方式是通過運行命令行。如果是在虛擬環境中安裝的 TensorFlow，需要激活虛擬環境。接著，在根目錄（也可以是其它路徑，但一定要指向日志目錄）運行下面的命令： ```py $ tensorboard --logdir=./my_logs --port=6006 TensorBoard 2.0.0 at http://mycomputer.local:6006/ (Press CTRL+C to quit) ``` 如果終端沒有找到`tensorboard`命令，必須更新環境變量 PATH（或者，可以使用`python3 -m tensorboard.main`）。服務啟動后，打開瀏覽器訪問 [*http://localhost:6006*](https://links.jianshu.com/go?to=http%3A%2F%2Flocalhost%3A6006%2F)。 或者，通過運行下面的命令，可以在 Jupyter 里面直接使用 TensorBoard。第一行代碼加載了 TensorBoard 擴展，第二行在端口 6006 啟動了一個 TensorBoard 服務，并連接： ```py %load_ext tensorboard %tensorboard --logdir=./my_logs --port=6006 ``` 無論是使用哪種方式，都得使用 TensorBoard 的瀏覽器界面。點擊欄`SCALARS`可以查看學習曲線（見圖 10-17）。左下角選擇想要可視化的路徑（比如第一次和第二次運行的訓練日志），再點擊`epoch_loss`。可以看到，在兩次訓練過程中，訓練損失都是下降的，但第二次下降的更快。事實上，第二次的學習率是 0.05（`optimizer=keras.optimizers.SGD(lr=0.05)`）而不是 0.001。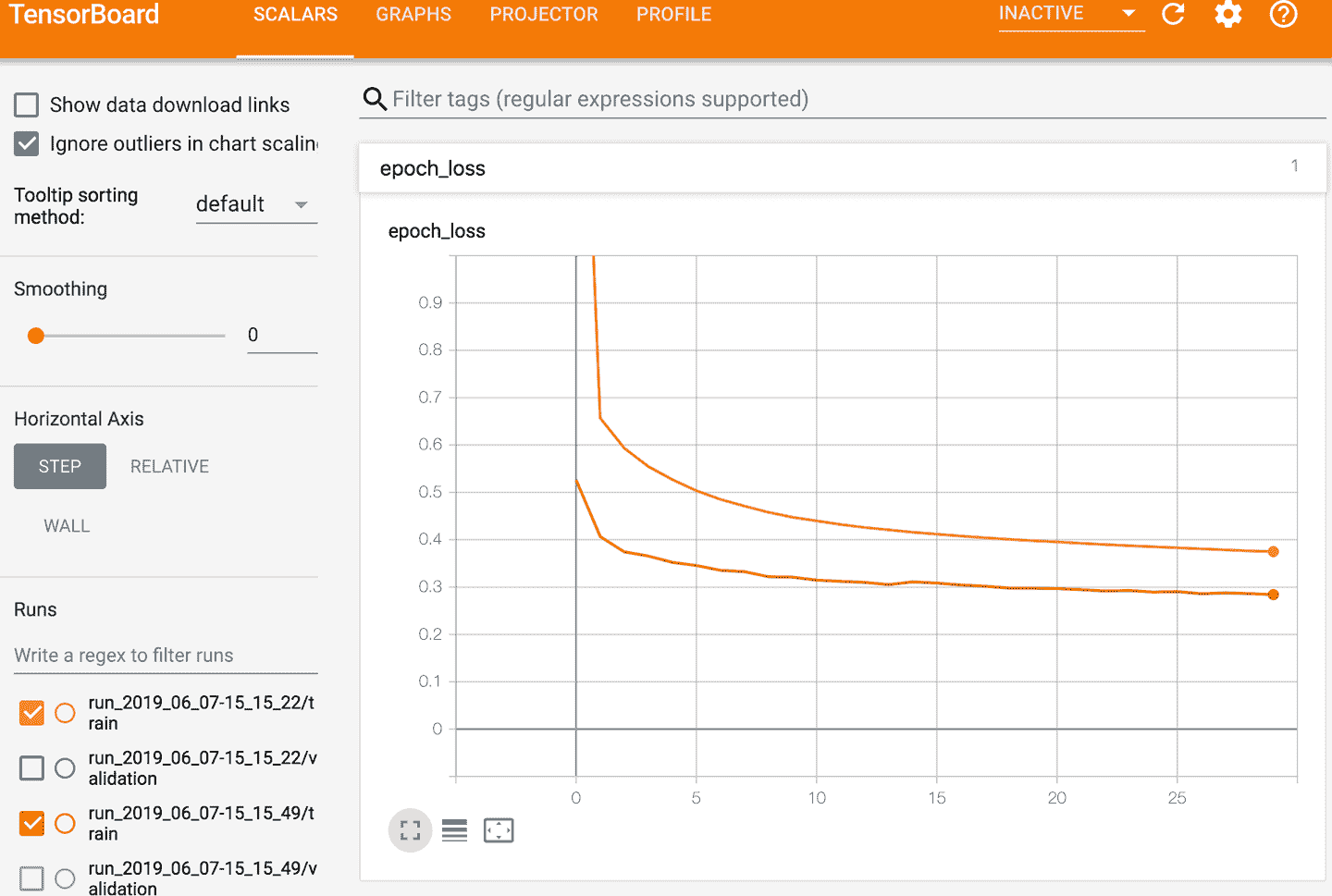 圖 10-17 使用 TensorBoard 可視化學習曲線 還可以對全圖、權重（投射到 3D）或其它信息做可視化。`TensorBoard()`調回還有選項可以記錄其它數據的日志，比如嵌入（見第 13 章）。另外，TensorBoard 在`tf.summary`包中還提供了低級 API。下面的代碼使用方法`create_file_writer()`創建了`SummaryWriter`，TensorBoard 使用`SummaryWriter`作為記錄標量、柱狀圖、圖片、音頻和文本的上下文，所有這些都是可以可視化的！ ```py test_logdir = get_run_logdir() writer = tf.summary.create_file_writer(test_logdir) with writer.as_default(): for step in range(1, 1000 + 1): tf.summary.scalar("my_scalar", np.sin(step / 10), step=step) data = (np.random.randn(100) + 2) * step / 100 # some random data tf.summary.histogram("my_hist", data, buckets=50, step=step) images = np.random.rand(2, 32, 32, 3) # random 32×32 RGB images tf.summary.image("my_images", images * step / 1000, step=step) texts = ["The step is " + str(step), "Its square is " + str(step**2)] tf.summary.text("my_text", texts, step=step) sine_wave = tf.math.sin(tf.range(12000) / 48000 * 2 * np.pi * step) audio = tf.reshape(tf.cast(sine_wave, tf.float32), [1, -1, 1]) tf.summary.audio("my_audio", audio, sample_rate=48000, step=step) ``` 總結一下目前所學：神經網絡的起源、MLP 是什么、如何用 MLP 做分類和回歸、如何使用 Sequential API 搭建 MLP、如何使用 Functional API 或 Subclassing API 搭建更復雜的模型架構、保存和恢復模型、如何使用調回創建檢查點、早停，等等。最后，學了使用 TensorBoard 做可視化。這些知識已經足夠解決許多問題了。但是，你可能還有疑問，如何選擇隱藏層的層數、神經元的數量，以及其他的超參數，下面就來討論這些問題。 ### 微調神經網絡的超參數 神經網絡的靈活性同時也是它的缺點：要微調的超參數太多了。不僅架構可能不同，就算對于一個簡單的 MLP，就可以調節層數、每層的神經元數、每層使用什么激活函數、初始化的權重，等等。怎么才能知道哪個超參數的組合才是最佳的呢？ 一種方法是直接試驗超參數的組合，看哪一個在驗證集（或使用 K 折交叉驗證）的表現最好。例如，可以使用`GridSearchCV`或`RandomizedSearchCV`探索超參數空間，就像第 2 章中那樣。要這么做的話，必須將 Keras 模型包裝進模仿 Scikit-Learn 回歸器的對象中。第一步是給定一組超參數，創建一個搭建和編譯 Keras 模型的函數： ```py def build_model(n_hidden=1, n_neurons=30, learning_rate=3e-3, input_shape=[8]): model = keras.models.Sequential() model.add(keras.layers.InputLayer(input_shape=input_shape)) for layer in range(n_hidden): model.add(keras.layers.Dense(n_neurons, activation="relu")) model.add(keras.layers.Dense(1)) optimizer = keras.optimizers.SGD(lr=learning_rate) model.compile(loss="mse", optimizer=optimizer) return model ``` 這個函數創建了一個單回歸（只有一個輸出神經元）Sequential 模型，數據形狀、隱藏層的層數和神經元數是給定的，使用指定學習率的`SGD`優化器編譯。最好盡量給大多數超參數都設置合理的默認值，就像 Scikit-Learn 那樣。 然后使用函數`build_model()`創建一個`KerasRegressor`： ```py keras_reg = keras.wrappers.scikit_learn.KerasRegressor(build_model) ``` `KerasRegressor`是通過`build_model()`將 Keras 模型包裝起來的。因為在創建時沒有指定任何超參數，使用的是`build_model()`的默認參數。現在就可以像常規的 Scikit-Learn 回歸器一樣來使用它了：使用`fit()`方法訓練，使用`score()`方法評估，使用`predict()`方法預測，見下面代碼： ```py keras_reg.fit(X_train, y_train, epochs=100, validation_data=(X_valid, y_valid), callbacks=[keras.callbacks.EarlyStopping(patience=10)]) mse_test = keras_reg.score(X_test, y_test) y_pred = keras_reg.predict(X_new) ``` 任何傳給`fit()`的參數都會傳給底層的 Keras 模型。另外，score 分數的意義和 MSE 是相反的（即，分數越高越好）。因為超參數太多，最好使用隨機搜索而不是網格搜索（見第 2 章的解釋）。下面來探索下隱藏層的層數、神經元數和學習率： ```py from scipy.stats import reciprocal from sklearn.model_selection import RandomizedSearchCV param_distribs = { "n_hidden": [0, 1, 2, 3], "n_neurons": np.arange(1, 100), "learning_rate": reciprocal(3e-4, 3e-2), } rnd_search_cv = RandomizedSearchCV(keras_reg, param_distribs, n_iter=10, cv=3) rnd_search_cv.fit(X_train, y_train, epochs=100, validation_data=(X_valid, y_valid), callbacks=[keras.callbacks.EarlyStopping(patience=10)]) ``` 所做的和第 2 章差不多，除了這里試講參數傳給`fit()`，`fit()`再傳給底層的 Keras。注意，`RandomizedSearchCV`使用的是 K 折交叉驗證，沒有用`X_valid`和`y_valid`（只有早停時才使用）。 取決于硬件、數據集大小、模型復雜度、`n_iter`和`cv`，求解過程可能會持續幾個小時。計算完畢后，就能得到最佳參數、最佳得分和訓練好的 Keras 模型，如下所示： ```py >>> rnd_search_cv.best_params_ {'learning_rate': 0.0033625641252688094, 'n_hidden': 2, 'n_neurons': 42} >>> rnd_search_cv.best_score_ -0.3189529188278931 >>> model = rnd_search_cv.best_estimator_.model ``` 現在就可以保存模型、在測試集上評估，如果對效果滿意，就可以部署了。使用隨機搜索并不難，適用于許多相對簡單的問題。但是當訓練較慢時（大數據集的復雜問題），這個方法就只能探索超參數空間的一小部分而已。通過手動調節可以緩解一下：首先使用大范圍的超參數值先做一次隨機搜索，然后根據第一次的結果再做一次小范圍的計算，以此類推。這樣就能縮放到最優超參數的范圍了。但是，這么做很耗時。 幸好，有比隨機搜索更好的探索超參數空間的方法。核心思想很簡單：當某塊空間的區域表現好時，就多探索這塊區域。這些方法可以代替用戶做“放大”工作，可以在更短的時間得到更好的結果。下面是一些可以用來優化超參數的 Python 庫： [Hyperopt](https://links.jianshu.com/go?to=https%3A%2F%2Fgithub.com%2Fhyperopt%2Fhyperopt) 一個可以優化各種復雜搜索空間（包括真實值，比如學習率和離散值，比如層數）的庫。 [Hyperas](https://links.jianshu.com/go?to=https%3A%2F%2Fgithub.com%2Fmaxpumperla%2Fhyperas)，[kopt](https://links.jianshu.com/go?to=https%3A%2F%2Fgithub.com%2FAvsecz%2Fkopt) 或 [Talos](https://links.jianshu.com/go?to=https%3A%2F%2Fgithub.com%2Fautonomio%2Ftalos) 用來優化 Keras 模型超參數的庫（前兩個是基于 Hyperopt 的）。 [Keras Tuner](https://links.jianshu.com/go?to=https%3A%2F%2Fhoml.info%2Fkerastuner) Google 開發的簡單易用的 Keras 超參數優化庫，還有可視化和分析功能。 [Scikit-Optimize (`skopt`)](https://links.jianshu.com/go?to=https%3A%2F%2Fscikit-optimize.github.io%2F) 一個通用的優化庫。類`BayesSearchCV`使用類似于`GridSearchCV`的接口做貝葉斯優化。 [Spearmint](https://links.jianshu.com/go?to=https%3A%2F%2Fgithub.com%2FJasperSnoek%2Fspearmint) 一個貝葉斯優化庫。 [Hyperband](https://links.jianshu.com/go?to=https%3A%2F%2Fgithub.com%2Fzygmuntz%2Fhyperband) 一個快速超參數調節庫，基于 Lisha Li 的論文 《Hyperband: A Novel Bandit-Based Approach to Hyperparameter Optimization》，[https://arxiv.org/abs/1603.06560](https://links.jianshu.com/go?to=https%3A%2F%2Farxiv.org%2Fabs%2F1603.06560)。 [Sklearn-Deap](https://links.jianshu.com/go?to=https%3A%2F%2Fgithub.com%2Frsteca%2Fsklearn-deap) 一個基于進化算法的超參數優化庫，接口類似`GridSearchCV`。 另外，許多公司也提供超參數優化服務。第 19 章會討論 Google Cloud AI 平臺的超參數調節服務（[https://cloud.google.com/ml-engine/docs/tensorflow/using-hyperparameter-tuning](https://links.jianshu.com/go?to=https%3A%2F%2Fcloud.google.com%2Fml-engine%2Fdocs%2Ftensorflow%2Fusing-hyperparameter-tuning)）。其它公司有[Arimo](https://links.jianshu.com/go?to=https%3A%2F%2Farimo.com%2F) 、 [SigOpt](https://links.jianshu.com/go?to=https%3A%2F%2Fsigopt.com%2F)，和 CallDesk 的 [Oscar](https://links.jianshu.com/go?to=http%3A%2F%2Foscar.calldesk.ai%2F). 超參數調節仍然是活躍的研究領域，其中進化算法表現很突出。例如，在 2017 年的論文《Population Based Training of Neural Networks》（[https://arxiv.org/abs/1711.09846](https://links.jianshu.com/go?to=https%3A%2F%2Farxiv.org%2Fabs%2F1711.09846)）中，Deepmind 的作者用統一優化了一組模型及其超參數。Google 也使用了一種進化算法，不僅用來搜索查參數，還可以搜索最佳的神經網絡架構；Google 的 AutoML 套間已經可以在云服務上使用了（[https://cloud.google.com/automl/](https://links.jianshu.com/go?to=https%3A%2F%2Fcloud.google.com%2Fautoml%2F)）。也許手動搭建神經網絡的日子就要結束了？看看 Google 的這篇文章：[https://ai.googleblog.com/2018/03/using-evolutionary-automl-to-discover.html](https://links.jianshu.com/go?to=https%3A%2F%2Fai.googleblog.com%2F2018%2F03%2Fusing-evolutionary-automl-to-discover.html)。事實上，用進化算法訓練獨立的神經網絡很成功，已經取代梯度下降了。例如，Uber 在 2017 年介紹了名為 Deep Neuroevolution 的技術，見[https://eng.uber.com/deep-neuroevolution/](https://links.jianshu.com/go?to=https%3A%2F%2Feng.uber.com%2Fdeep-neuroevolution%2F)。 盡管有這些工具和服務，知道每個超參數該取什么值仍然是幫助的，可以快速創建原型和收縮搜索范圍。后面的文字介紹了選擇 MLP 隱藏層數和神經元數的原則，以及如何選擇主要的超參數值。 ### 隱藏層數 對于許多問題，開始時只用一個隱藏層就能得到不錯的結果。只要有足夠多的神經元，只有一個隱藏層的 MLP 就可以對復雜函數建模。但是對于復雜問題，深層網絡比淺層網絡有更高的參數效率：深層網絡可以用指數級別更少的神經元對復雜函數建模，因此對于同樣的訓練數據量性能更好。 要明白為什么，假設別人讓你用繪圖軟件畫一片森林，但你不能復制和粘貼。這樣的話，就得花很長時間，你需要手動來畫每一棵樹，一個樹枝然后一個樹枝，一片葉子然后一片葉子。如果可以鮮花一片葉子，然后將葉子復制粘貼到整個樹枝上，再將樹枝復制粘貼到整棵樹上，然后再復制樹，就可以畫出一片森林了，所用的時間可以大大縮短。真實世界的數據通常都是有層次化結構的，深層神經網絡正式利用了這一點：淺隱藏層對低級結構（比如各種形狀的線段和方向），中隱藏層結合這些低級結構對中級結構（方，圓）建模，深隱藏層和輸出層結合中級結構對高級結構（比如，臉）建模。 層級化的結構不僅幫助深度神經網絡收斂更快，，也提高了對新數據集的泛化能力。例如，如果已經訓練好了一個圖片人臉識別的模型，現在想訓練一個識別發型的神經網絡，你就可以復用第一個網絡的淺層。不用隨機初始化前幾層的權重和偏置項，而是初始化為第一個網絡淺層的權重和偏置項。這樣，網絡就不用從多數圖片的低級結構開始學起；只要學高級結構（發型）就行了。這就稱為遷移學習。 概括來講，對于許多問題，神經網絡只有一或兩層就夠了。例如，只用一個隱藏層和幾百個神經元，就能在 MNIST 上輕松達到 97%的準確率；同樣的神經元數，兩個隱藏層，訓練時間幾乎相同，就能達到 98%的準確率。對于更復雜的問題，可以增加隱藏層的數量，直到在訓練集上過擬合為止。非常復雜的任務，比如大圖片分類或語音識別，神經網絡通常需要幾十層（甚至上百，但不是全連接的，見第 14 章），需要的訓練數據量很大。對于這樣的網絡，很少是從零訓練的：常見的是使用預訓練好的、表現出眾的任務相近的網絡，訓練可以快得多，需要的數據也可以不那么多（見第 11 章的討論）。 ### 每個隱藏層的神經元數 輸入層和輸出層的神經元數是由任務確定的輸入和輸出類型決定的。例如，MNIST 任務需要 28 × 28 = 784 個輸入神經元和 10 個輸出神經元。 對于隱藏層，慣用的方法是模擬金字塔的形狀，神經元數逐層遞減 —— 底層思想是，許多低級特征可以聚合成少得多的高級特征。MNIST 的典型神經網絡可能需要 3 個隱藏層，第一層有 300 個神經元，第二層有 200 個神經元，第三層有 100 個神經元。然而，這種方法已經被拋棄了，因為所有隱藏層使用同樣多的神經元不僅表現更好，要調節的超參數也只變成了一個，而不是每層都有一個。或者，取決于數據集的情況，有時可以讓第一個隱藏層比其它層更大。 和層數相同，可以逐步提高神經元的數量，知道發生過擬合為止。但在實際中，通常的簡便而高效的方法是使用層數和神經元數都超量的模型，然后使用早停和其它正則技術防止過擬合。一位 Google 的科學家 Vincent Vanhoucke，稱這種方法為“彈力褲”：不浪費時間選擇尺寸完美匹配的褲子，而是選擇一條大的彈力褲，它能自動收縮到合適的尺寸。通過這種方法，可以避免影響模型的瓶頸層。另一方面，如果某層的神經元太少，就沒有足夠強的表征能力，保存所有的輸入信息（比如，只有兩個神經元的的層只能輸出 2D 數據，如果用它處理 3D 數據，就會丟失信息）。無論模型網絡的其它部分如何強大，丟失的信息也找不回來了。 > 提示：通常，增加層數比增加每層的神經元的收益更高。 ### 學習率，批次大小和其它超參數 隱藏層的層數和神經元數不是 MLP 唯二要調節的參數。下面是一些其它的超參數和調節策略： 學習率： 學習率可能是最重要的超參數。通常，最佳學習率是最大學習率（最大學習率是超過一定值，訓練算法發生分叉的學習率，見第 4 章）的大概一半。找到最佳學習率的方式之一是從一個極小值開始（比如 10^-5）訓練模型幾百次，直到學習率達到一個比較大的值（比如 10）。這是通過在每次迭代，將學習率乘以一個常數實現的（例如 exp(log(10⁶)/500，通過 500 次迭代，從 10^-5到 10 ）。如果將損失作為學習率的函數畫出來（學習率使用 log），能看到損失一開始是下降的。過了一段時間，學習率會變得非常高，損失就會升高：最佳學習率要比損失開始升高的點低一點（通常比拐點低 10 倍）。然后就可以重新初始化模型，用這個學習率開始訓練了。第 11 章會介紹更多的學習率優化方法。 優化器： 選擇一個更好的優化器（并調節超參數）而不是傳統的小批量梯度下降優化器同樣重要。第 11 章會介紹更先進的優化器。 批次大小： 批次大小對模型的表現和訓練時間非常重要。使用大批次的好處是硬件（比如 GPU）可以快速處理（見第 19 章），每秒可以處理更多實例。因此，許多人建議批次大小開到 GPU 內存的最大值。但也有缺點：在實際中，大批次，會導致訓練不穩定，特別是在訓練開始時，并且不如小批次模型的泛化能力好。2018 年四月，Yann LeCun 甚至發了一條推特：“朋友之間不會讓對方的批次大小超過 32”，引用的是 Dominic Masters 和 Carlo Luschi 的論文《Revisiting Small Batch Training for Deep Neural Networks》（[https://arxiv.org/abs/1804.07612](https://links.jianshu.com/go?to=https%3A%2F%2Farxiv.org%2Fabs%2F1804.07612)），在這篇論文中，作者的結論是小批次（2 到 32）更可取，因為小批次可以在更短的訓練時間得到更好的模型。但是，有的論文的結論截然相反：2017 年，兩篇論文[《Train longer, generalize better: closing the generalization gap in large batch training of neural networks》](https://links.jianshu.com/go?to=https%3A%2F%2Farxiv.org%2Fabs%2F1705.08741)和[《Accurate, Large Minibatch SGD: Training ImageNet in 1 Hour》](https://links.jianshu.com/go?to=https%3A%2F%2Farxiv.org%2Fabs%2F1706.02677)建議，通過多種方法，比如給學習率熱身（即學習率一開始很小，然后逐漸提高，見第 11 章），就能使用大批次（最大 8192）。這樣，訓練時間就能非常短，也沒有泛化鴻溝。因此，一種策略是通過學習率熱身使用大批次，如果訓練不穩定或效果不好，就換成小批次。 激活函數： 本章一開始討論過如何選擇激活函數：通常來講，ReLU 適用于所有隱藏層。對于輸出層，就要取決于任務。 迭代次數： 對于大多數情況，用不著調節訓練的迭代次數：使用早停就成了。 > 提示：最佳學習率還取決于其它超參數，特別是批次大小，所以如果調節了任意超參數，最好也更新學習率。 想看更多關于調節超參數的實踐，可以參考 Leslie Smith 的論文[《A disciplined approach to neural network hyper-parameters: Part 1 -- learning rate, batch size, momentum, and weight decay》](https://links.jianshu.com/go?to=https%3A%2F%2Farxiv.org%2Fabs%2F1803.09820)。 這章總結了對人工神經網絡，以及 Kera 是實現。接下來的章節，我們會討論訓練深層網絡的方法。還會使用 TensorFlow 的低級 API 實現自定義模型，和使用 Data API 高效加載和預處理數據。還會探討其它流行的神經網絡：用于圖像處理的卷積神經網絡，用于序列化數據的循環神經網絡，用于表征學習的自編碼器，用于建模和生成數據的對抗生成網絡。 # 練習 1. [TensorFlow Playground](https://links.jianshu.com/go?to=https%3A%2F%2Fplayground.tensorflow.org%2F)是 TensorFlow 團隊推出的一個便利的神經網絡模擬器。只需點擊幾下，就能訓練出二元分類器，通過調整架構和超參數，可以從直觀上理解神經網絡是如何工作的，以及超參數的作用。如下所示： a. 神經網絡學到的模式。點擊左上的運行按鈕，訓練默認的神經網絡。注意是如何找到分類任務的最優解的。第一個隱藏層學到了簡單模式，第二個隱藏層將簡單模式結合為更復雜的模式。通常，層數越多，得到的模式越復雜。 b. 激活函數。用 ReLU 激活函數代替 tanh，再訓練一次網絡。注意，找到解變得更快了，且是線性的，這歸功于 ReLU 函數的形狀。 c. 局部最小值的風險。將網絡只設定為只有一個隱藏層，且只有 3 個神經元。進行多次訓練（重置網絡權重，點擊 Reset 按鈕）。可以看到訓練時間變化很大，甚至有時卡在了局部最小值。 d. 神經網絡太小的狀況。去除一個神經元，只剩下兩個。可以看到，即使嘗試多次，神經網絡現也不能找到最優解。模型的參數太少，對訓練集數據欠擬合。 e. 神經網絡足夠大的狀況。將神經元數設為 8，再多次訓練神經網絡。可以看到過程很快且不會卡住。這是一個重要的發現：大神經網絡幾乎從不會卡在局部最小值，即使卡住了，局部最小值通常也是全局最小值。但是仍然可能在平臺期卡住相當長時間。 f. 梯度消失的風險。選擇 spiral 數據集（右下角位于 DATA 下面的數據集），模型架構變為四個隱藏層，每層八個神經元。可以看到，訓練耗時變長，且經常在平臺期卡住很長時間。另外，最高層（右邊）的神經元比最底層變得快。這個問題被稱為“梯度消失”，可以通過更優的權重初始化、更好的優化器（比如 AdaGrad 或 Adam）、或批次正態化（見第 11 章）解決。 g. 再嘗試嘗試其它參數。 2. 用原始神經元（像圖 10-3 中的神經元）畫 ANN，可以計算 A ⊕ B （ ⊕ 表示 XOR 操作）。提示：A ⊕ B = (A ∧ ? B ∨ (? A ∧ B) 3. 為什么邏輯回歸比經典感知機（即使用感知機訓練算法訓練的單層的閾值邏輯單元）更好？如何調節感知機，使其等同于邏輯回歸分類器？ 4. 為什么邏輯激活函數對訓練 MLP 的前幾層很重要？ 5. 說出三種流行的激活函數，并畫出來。 6. 假設一個 MLP 的輸入層有 10 個神經元，接下來是有 50 個人工神經元的的隱藏層，最后是一個有 3 個人工神經元的輸出層。所有的神經元使用 ReLU 激活函數。回答以下問題： * 輸入矩陣 X 的形狀是什么？ * 隱藏層的權重矢量 W_h和偏置項 b_h的形狀是什么? * 輸出層的權重矢量 W_o和偏置項 b_o的形狀是什么? * 輸出矩陣 Y 的形狀是什么？ * 寫出用 X、W_h、b_h、W_o、b_o計算矩陣 Y 的等式。 7. 如果要將郵件分為垃圾郵件和正常郵件，輸出層需要幾個神經元？輸出層應該使用什么激活函數？如果任務換成 MNIST，輸出層需要多少神經元，激活函數是什么？再換成第 2 章中的房價預測，輸出層又該怎么變？ 8. 反向傳播是什么及其原理？反向傳播和逆向 autodiff 有什么不同？ 9. 列出所有簡單 MLP 中需要調節的超參數？如果 MLP 過擬合訓練數據，如何調節超參數？ 10. 在 MNIST 數據及上訓練一個深度 MLP。 使用`keras.datasets.mnist.load_data()`加載數據，看看能否使準確率超過 98%，利用本章介紹的方法（逐步指數級提高學習率，畫誤差曲線，找到誤差升高的點）搜索最佳學習率。保存檢查點，使用早停，用 TensorBoard 畫學習曲線的圖。 參考答案見附錄 A。