# 十一、訓練深度神經網絡
> 譯者:[@SeanCheney](https://www.jianshu.com/u/130f76596b02)
第 10 章介紹了人工神經網絡,并訓練了第一個深度神經網絡。 但它非常淺,只有兩個隱藏層。 如果你需要解決非常復雜的問題,例如檢測高分辨率圖像中的數百種類型的對象,該怎么辦? 你可能需要訓練更深的 DNN,也許有 10 層或更多,每層包含數百個神經元,通過數十萬個連接相連。 這可不像公園散步那么簡單,可能碰到下面這些問題:
* 你將面臨棘手的梯度消失問題(或相關的梯度爆炸問題):在反向傳播過程中,梯度變得越來越小或越來越大。二者都會使較淺層難以訓練;
* 要訓練一個龐大的神經網絡,但是數據量不足,或者標注成本很高;
* 訓練可能非常慢;
* 具有數百萬參數的模型將會有嚴重的過擬合訓練集的風險,特別是在訓練實例不多或存在噪音時。
在本章中,我們將依次討論這些問題,并給出解決問題的方法。 我們將從梯度消失/爆炸問題開始,并探討解決這個問題的一些最流行的解決方案。 接下來會介紹遷移學習和無監督預訓練,這可以在即使標注數據不多的情況下,也能應對復雜問題。然后我們將看看各種優化器,可以加速大型模型的訓練。 最后,我們將瀏覽一些流行的大型神經網絡正則化方法。
使用這些工具,你將能夠訓練非常深的網絡:歡迎來到深度學習的世界!
## 梯度消失/爆炸問題
正如我們在第 10 章中所討論的那樣,反向傳播算法的工作原理是從輸出層到輸入層,傳播誤差的梯度。 一旦該算法已經計算了網絡中每個參數的損失函數的梯度,它就通過梯度下降使用這些梯度來更新每個參數。
不幸的是,隨著算法進展到較低層,梯度往往變得越來越小。 結果,梯度下降更新使得低層連接權重實際上保持不變,并且訓練永遠不會收斂到最優解。 這被稱為梯度消失問題。 在某些情況下,可能會發生相反的情況:梯度可能變得越來越大,許多層得到了非常大的權重更新,算法發散。這是梯度爆炸的問題,在循環神經網絡中最為常見(見第 145 章)。 更一般地說,深度神經網絡面臨梯度不穩定; 不同的層可能有非常不同的學習率。
雖然很早就觀察到這種現象了(這是造成深度神經網絡在 2000 年早期被拋棄的原因之一),但直到 2010 年左右,人們才才略微清楚了導致梯度消失/爆炸的原因。 Xavier Glorot 和 Yoshua Bengio 發表的題為《Understanding the Difficulty of Training Deep Feedforward Neural Networks》([http://proceedings.mlr.press/v9/glorot10a/glorot10a.pdf](https://links.jianshu.com/go?to=http%3A%2F%2Fproceedings.mlr.press%2Fv9%2Fglorot10a%2Fglorot10a.pdf))的論文發現了一些疑點,包括流行的 sigmoid 激活函數和當時最受歡迎的權重初始化方法的組合,即隨機初始化時使用平均值為 0,標準差為 1 的正態分布。簡而言之,他們表明,用這個激活函數和這個初始化方案,每層輸出的方差遠大于其輸入的方差。隨著網絡前向傳播,每層的方差持續增加,直到激活函數在頂層飽和。logistic 函數的平均值為 0.5 而不是 0(雙曲正切函數的平均值為 0,表現略好于深層網絡中的 logistic 函數),使得情況更壞。
看一下 logistic 激活函數(參見圖 11-1),可以看到當輸入變大(負或正)時,函數飽和在 0 或 1,導數非常接近 0。因此,當反向傳播開始時, 它幾乎沒有梯度通過網絡傳播回來,而且由于反向傳播通過頂層向下傳遞,所以存在的小梯度不斷地被稀釋,因此較低層得到的改善很小。
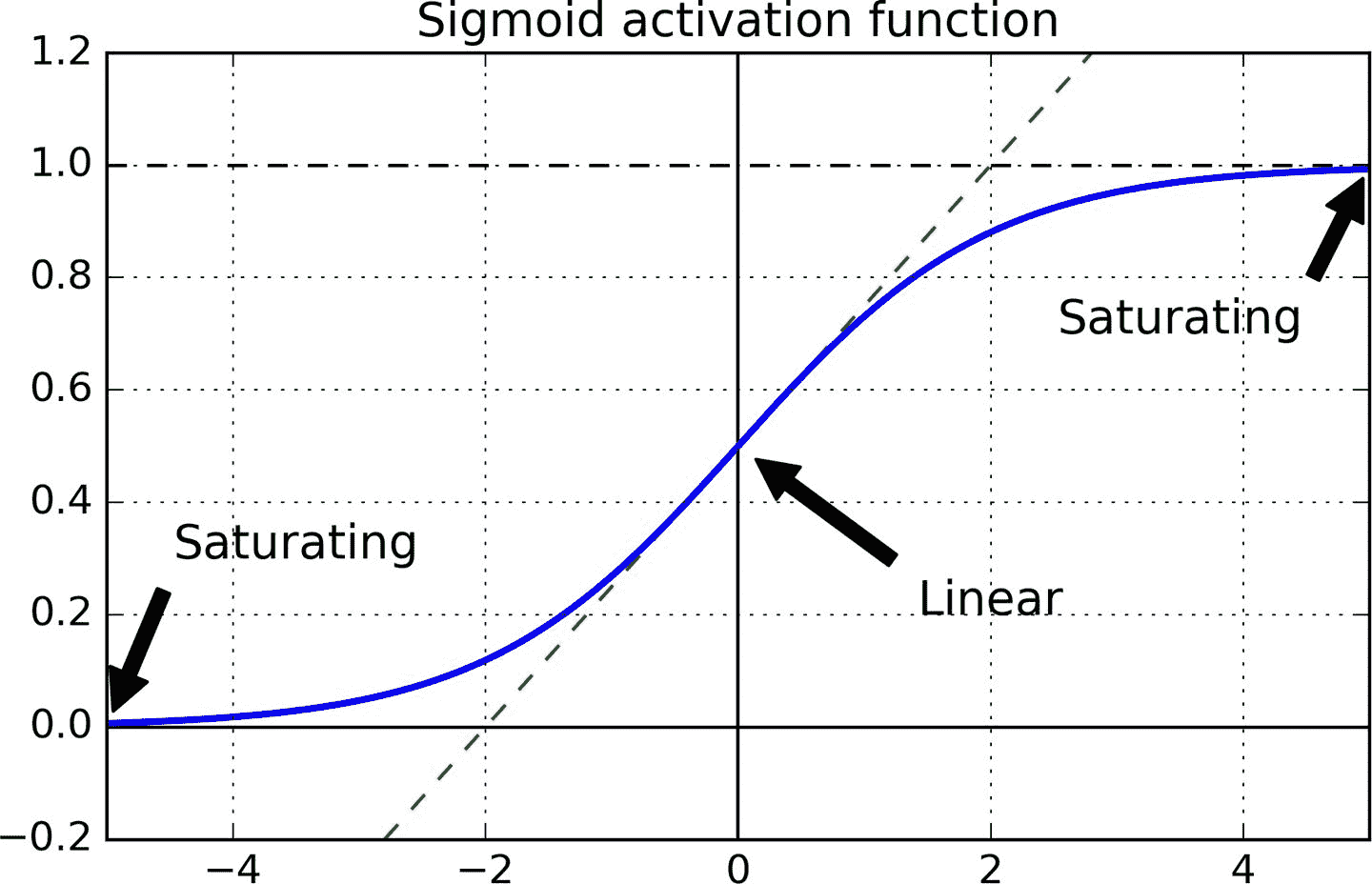圖 11-1 邏輯激活函數飽和
### Glorot 和 He 初始化
Glorot 和 Bengio 在他們的論文中提出了一種顯著緩解這個問題的方法。 我們需要信號在兩個方向上正確地流動:在進行預測時是前向的,在反向傳播梯度時是逆向的。 我們不希望信號消失,也不希望它爆炸并飽和。 為了使信號正確流動,作者認為,我們需要每層輸出的方差等于其輸入的方差,并且反向傳播時,流經一層的前后,梯度的方差也要相同(如果對數學細節感興趣的話,請查看論文)。實際上不可能保證兩者都是一樣的,除非這個層具有相同數量的輸入和神經元(這兩個數被稱為該層的扇入`fan-in`和扇出`fan-out`),但是他們提出了一個很好的折衷辦法,在實踐中證明這個折中辦法非常好:隨機初始化連接權重必須如公式 11-1 這樣,其中 fan<sub>avg</sub> = (fan<sub>in</sub> + fan<sub>out</sub>) / 2。 這種初始化策略通常被稱為 Xavier 初始化或 Glorot 初始化。
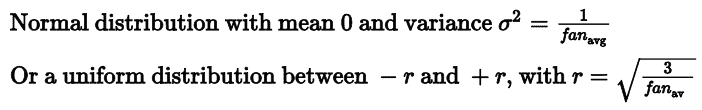公式 11-1 Xavier 初始化(使用邏輯激活函數)
如果將公式 11-1 中的 fan<sub>avg</sub>替換為 fan<sub>in</sub>,就得到了 Yann LeCun 在 1990 年代提出的初始化策略,他稱其為 LeCun 初始化。Genevieve Orr 和 Klaus-Robert Müller 在 1998 年出版的書《Neural Networks: Tricks of the Trade (Springer)》中推薦了 LeCun 初始化。當 fan<sub>in</sub> = fan<sub>out</sub> 時,LeCun 初始化等同于 Glorot 初始化。研究者們經歷了十多年才意識到初始化策略的重要性。使用 Glorot 初始化可以大大加快訓練,這是促成深度學習成功的技術之一。
一些論文針對不同的激活函數提供了類似的策略。這些策略的區別在于方差大小和使用 fan<sub>avg</sub>或 fan<sub>out</sub>,如表 11-1 所示。 ReLU 激活函數(及其變體,包括簡稱 ELU 激活)的初始化策略有時稱為 He 初始化。本章后面會介紹 SELU 激活函數,它應該與 LeCun 初始化(最好是正態分布)一起使用。
表 11-1 每種激活函數的初始化參數
默認情況下,Keras 使用均勻分布的 Glorot 初始化函數。創建層時,可以通過設置`kernel_initializer="he_uniform"`或`kernel_initializer="he_normal"`變更為 He 初始化,如下所示:
```py
keras.layers.Dense(10, activation="relu", kernel_initializer="he_normal")
```
如果想讓均勻分布的 He 初始化是基于 fan<sub>avg</sub>而不是 fan<sub>in</sub>,可以使用 VarianceScaling 初始化器:
```py
he_avg_init = keras.initializers.VarianceScaling(scale=2., mode='fan_avg',
distribution='uniform')
keras.layers.Dense(10, activation="sigmoid", kernel_initializer=he_avg_init)
```
### 非飽和激活函數
Glorot 和 Bengio 在 2010 年的論文中的一個見解是,消失/爆炸的梯度問題部分是由于激活函數的選擇不好造成的。 在那之前,大多數人都認為,如果大自然選擇在生物神經元中使用 sigmoid 激活函數,它們必定是一個很好的選擇。 但事實證明,其他激活函數在深度神經網絡中表現得更好,特別是 ReLU 激活函數,主要是因為它對正值不會飽和(也因為它的計算速度很快)。
但是,ReLU 激活功能并不完美。 它有一個被稱為 “ReLU 死區” 的問題:在訓練過程中,一些神經元會“死亡”,即它們停止輸出 0 以外的任何東西。在某些情況下,你可能會發現你網絡的一半神經元已經死亡,特別是使用大學習率時。 在訓練期間,如果神經元的權重得到更新,使得神經元輸入的加權和為負,則它將開始輸出 0 。當這種情況發生時,由于當輸入為負時,ReLU 函數的梯度為 0,神經元就只能輸出 0 了。
為了解決這個問題,你可能需要使用 ReLU 函數的一個變體,比如 leaky ReLU。這個函數定義為 LeakyReLU<sub>α</sub>(z)= max(αz,z)(見圖 11-2)。超參數`α`定義了函數“leak”的程度:它是`z < 0`時函數的斜率,通常設置為 0.01。這個小斜率保證 leaky ReLU 永不死亡;他們可能會長期昏迷,但他們有機會最終醒來。2015 年的一篇論文([https://arxiv.org/abs/1505.00853](https://links.jianshu.com/go?to=https%3A%2F%2Farxiv.org%2Fabs%2F1505.00853))比較了幾種 ReLU 激活功能的變體,其中一個結論是 leaky Relu 總是優于嚴格的 ReLU 激活函數。事實上,設定`α= 0.2`(大 leak)似乎比`α= 0.01`(小 leak)有更好的性能。這篇論文還評估了隨機化 leaky ReLU(RReLU),其中`α`在訓練期間在給定范圍內隨機,并在測試期間固定為平均值。它表現相當好,似乎是一個正則項(減少訓練集的過擬合風險)。最后,文章還評估了參數化的 leaky ReLU(PReLU),其中`α`被授權在訓練期間參與學習(而不是作為超參數,`α`變成可以像任何其他參數一樣被反向傳播修改的參數)。據報道,PReLU 在大型圖像數據集上的表現強于 ReLU,但是對于較小的數據集,其具有過度擬合訓練集的風險。
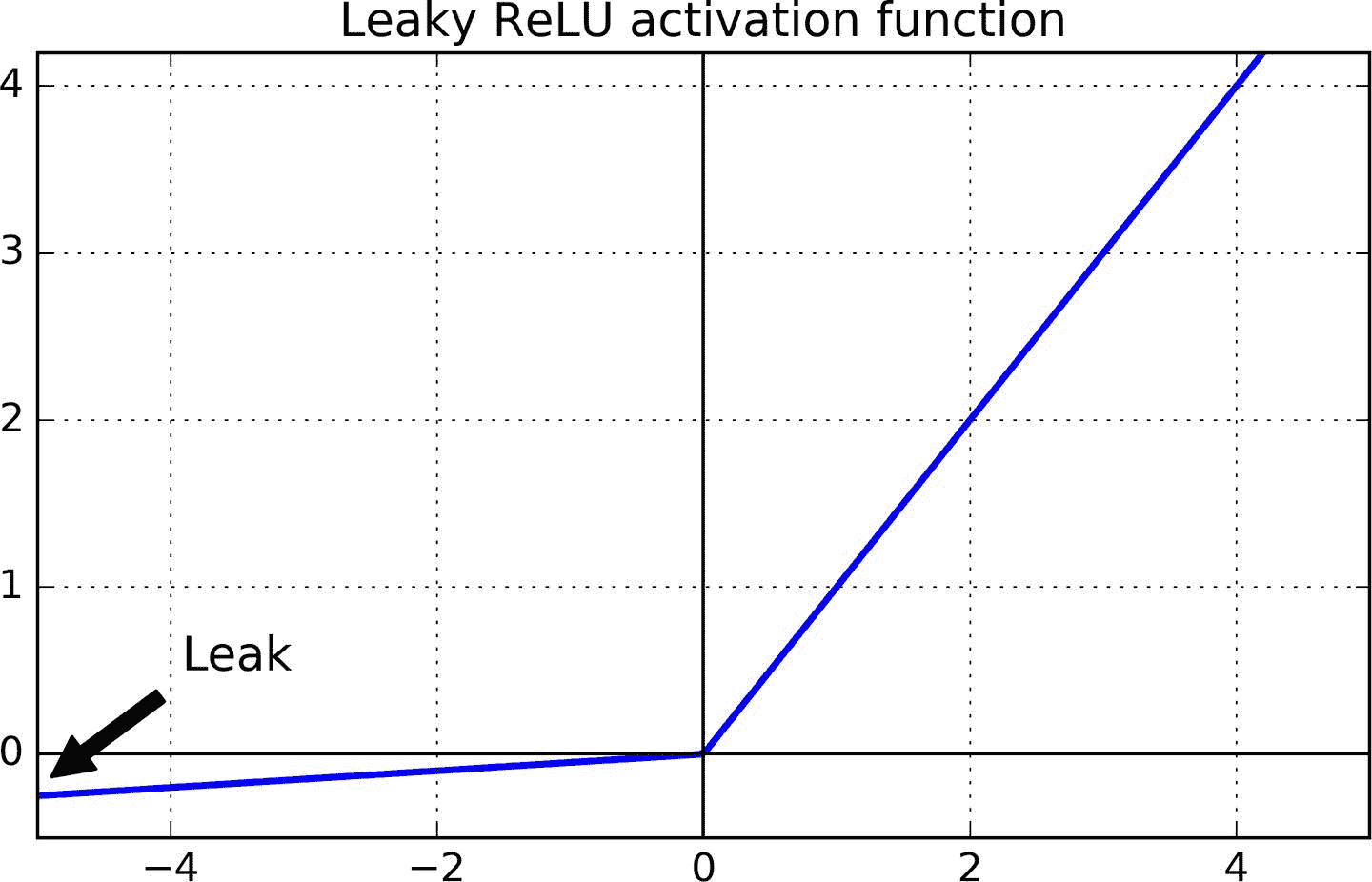圖 11-2 Leaky ReLU:很像 ReLU,但在負區間有小斜率
最后,Djork-Arné Clevert 等人在 2015 年的一篇論文([https://arxiv.org/abs/1511.07289](https://links.jianshu.com/go?to=https%3A%2F%2Farxiv.org%2Fabs%2F1511.07289))中提出了一種稱為指數線性單元(exponential linear unit,ELU)的新激活函數,在他們的實驗中,ELU 的表現優于所有 ReLU 變體:訓練時間減少,神經網絡在測試集上表現的更好。 如圖 11-3 所示,公式 11-2 給出了它的定義。
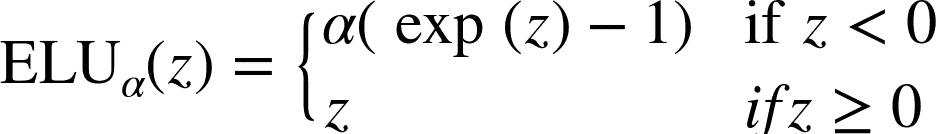公式 11-2 ELU 激活函數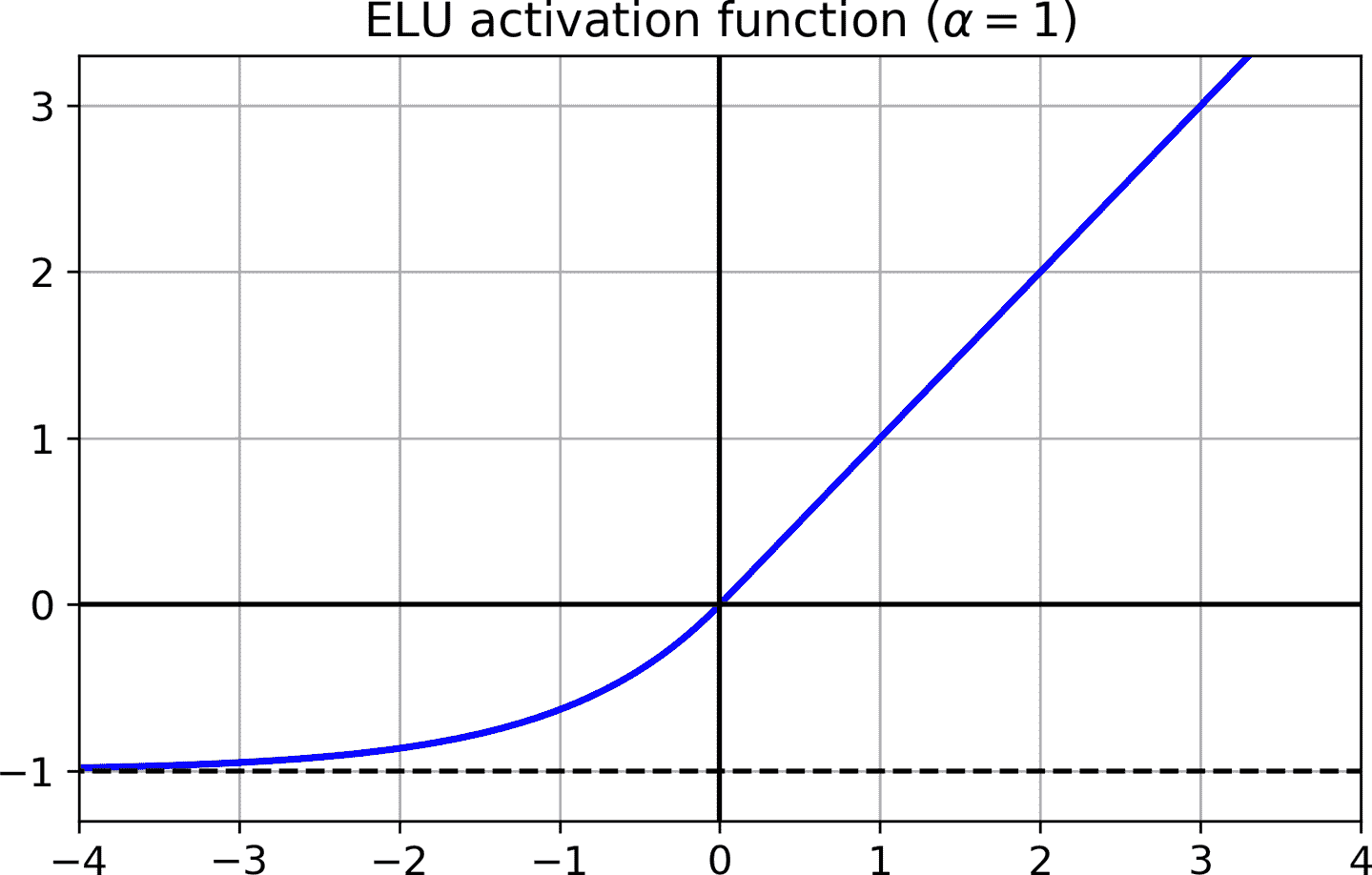圖 11-3 ELU 激活函數
ELU 看起來很像 ReLU 函數,但有一些區別,主要區別在于:
* 它在`z < 0`時取負值,這使得該單元的平均輸出接近于 0。這有助于減輕梯度消失問題。 超參數`α`定義為當`z`是一個大的負數時,ELU 函數接近的值。它通常設置為 1,但是如果你愿意,你可以像調整其他超參數一樣調整它。
* 它對`z < 0`有一個非零的梯度,避免了神經元死亡的問題。
* 如果`α`等于 1,則函數在任何地方都是平滑的,包括`z = 0`附近,這有助于加速梯度下降,因為它不會在`z = 0`附近回彈。
ELU 激活函數的主要缺點是計算速度慢于 ReLU 及其變體(由于使用指數函數),但是在訓練過程中,這是通過更快的收斂速度來補償的。 然而,在測試時間,ELU 網絡將比 ReLU 網絡慢。
2017 年的一篇文章([https://arxiv.org/abs/1706.02515](https://links.jianshu.com/go?to=https%3A%2F%2Farxiv.org%2Fabs%2F1706.02515))中,Günter Klambauer 等人介紹了一種 Scaled ELU(SELU)激活函數:正如它的名字所示,它是 ELU 的伸縮變體。作者證明,只要神經網絡中都是緊密層,并且所有隱藏層都是用的 SELU 激活函數,則這個網絡是自歸一的:訓練過程中,每層輸出的平均值是 0,標準差是 1,這樣就解決了梯度消失爆炸問題。對于全緊密層的網絡(尤其是很深的),SELU 的效果常常優于其他激活函數。但是自歸一是需要條件的(數學論證見論文):
* 輸入特征必須是標準的(平均值是 0,標準差是 1);
* 每個隱藏層的權重必須是 LeCun 正態初始化的。在 Keras 中,要設置`kernel_initializer="lecun_normal"`;
* 網絡架構必須是順序的。但是,如果要在非順序網絡(比如 RNN)或有跳連接的網絡(跳過層的連接,比如 Wide&Deep)中使用 SELU,就不能保證是自歸一的,所以 SELU 就不會比其它激活函數更優;
* 這篇論文只是說如果所有層都是緊密層才保證自歸一,但有些研究者發現 SELU 激活函數也可以提高卷積神經網絡的性能。
> 提示:那么深層神經網絡的隱藏層應該使用哪個激活函數呢? 雖然可能會有所不同,一般來說 SELU > ELU > leaky ReLU(及其變體)> ReLU > tanh > sigmoid。 如果網絡架構不能保證自歸一,則 ELU 可能比 SELU 的性能更好(因為 SELU 在 z=0 時不是平滑的)。如果關心運行延遲,則 leaky ReLU 更好。 如果你不想多調整另一個超參數,你可以使用前面提到的默認的`α`值(leaky ReLU 為 0.3)。 如果有充足的時間和計算能力,可以使用交叉驗證來評估其他激活函數,如果神經網絡過擬合,則使用 RReLU; 如果您擁有龐大的訓練數據集,則為 PReLU。但是,因為 ReLU 是目前應用最廣的激活函數,許多庫和硬件加速器都使用了針對 ReLU 的優化,如果速度是首要的,ReLU 可能仍然是首選。
要使用 leaky ReLU,需要創建一個`LeakyReLU`層,并將它加到需要追加的層后面:
```py
model = keras.models.Sequential([
[...]
keras.layers.Dense(10, kernel_initializer="he_normal"),
keras.layers.LeakyReLU(alpha=0.2),
[...]
])
```
對于 PReLU,用`PReLU()`替換`LeakyRelu(alpha=0.2)`。目前還沒有 RReLU 的 Keras 官方實現,但很容易自己實現(方法見第 12 章的練習)。
對于 SELU,當創建層時設置`activation="selu"`,`kernel_initializer="lecun_normal"`:
```py
layer = keras.layers.Dense(10, activation="selu",
kernel_initializer="lecun_normal")
```
### 批歸一化(Batch Normalization)
盡管使用 He 初始化和 ELU(或任何 ReLU 變體)可以顯著減少訓練開始階段的梯度消失/爆炸問題,但不能保證在訓練期間問題不會再次出現。
在 2015 年的一篇論文([https://arxiv.org/abs/1502.03167](https://links.jianshu.com/go?to=https%3A%2F%2Farxiv.org%2Fabs%2F1502.03167))中,Sergey Ioffe 和 Christian Szegedy 提出了一種稱為批歸一化(Batch Normalization,BN)的方法來解決梯度消失/爆炸問題。該方法包括在每層的激活函數之前或之后在模型中添加操作。操作就是將輸入平均值變為 0,方差變為 1,然后用兩個新參數,一個做縮放,一個做偏移。換句話說,這個操作可以讓模型學習到每層輸入值的最佳縮放值和平均值。大大多數情況下,如果模型的第一層使用了 BN 層,則不用標準化訓練集(比如使用`StandardScaler`);BN 層做了標準化工作(雖然是近似的,每次每次只處理一個批次,但能做縮放和平移)。
為了對輸入進行零居中(平均值是 0)和歸一化,算法需要估計輸入的均值和標準差。 它通過評估當前小批量輸入的均值和標準差(因此命名為“批歸一化”)來實現。 整個操作在公式 11-3 中。
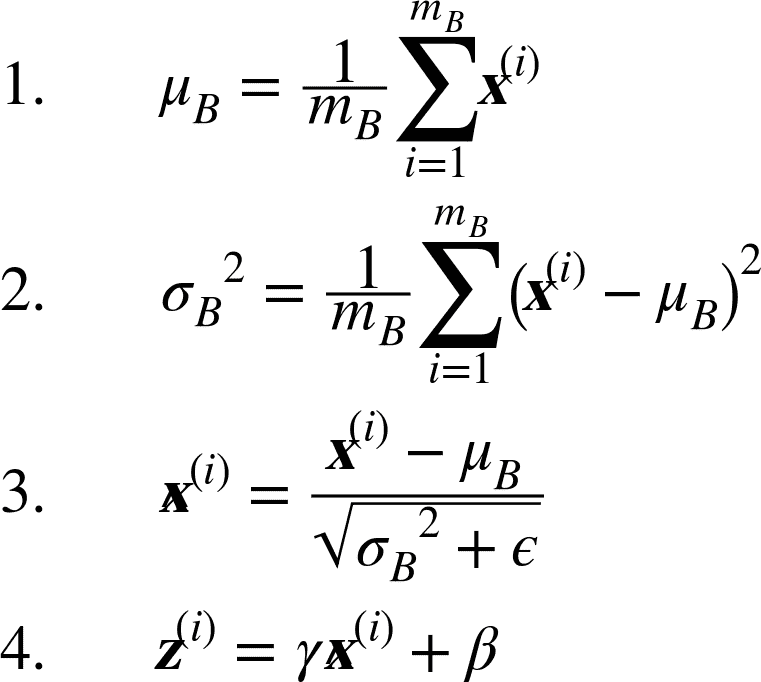公式 11-3 批歸一化算法
其中,
* μ<sub>B</sub>是整個小批量 B 的均值矢量
* σ<sub>B</sub>是輸入標準差矢量,也是根據整個小批量估算的。
* m<sub>B</sub>是小批量中的實例數量。
* 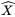<sup>(i)</sup>是以為零中心和標準化的實例 i 的輸入矢量。
* γ是層的縮放參數的矢量(每個輸入一個縮放參數)。
* ?表示元素級別的相乘(每個輸入乘以對應的縮放參數)
* β是層的偏移參數(偏移量)矢量(每個輸入一個偏移參數)
* ?是一個很小的數字,以避免被零除(通常為`10^-5`)。 這被稱為平滑項(拉布拉斯平滑,Laplace Smoothing)。
* z<sup>(i)</sup> 是 BN 操作的輸出:它是輸入的縮放和移位版本。
在訓練時,BN 將輸入標準化,然后做了縮放和平移。測試時又如何呢?因為需要對實例而不是批次實例做預測,所以就不能計算每個輸入的平均和標準差。另外,即使有批量實例,批量也可能太小,或者實例并不是獨立同分布的,所以在批量上計算是不可靠的。一種解決方法是等到訓練結束,用模型再運行一次訓練集,算出每個 BN 層的平均值和標準差。然后就可以用這些數據做預測,而不是批輸入的平均值和標準差。但是,大部分批歸一化實現是通過層輸入的平均值和標準差的移動平均值來計算的。這也是 Keras 在`BatchNormalization`中使用的方法。總的來說,每個批歸一化的層都通過指數移動平均學習了四個參數:`γ`(輸出縮放矢量),`β`(輸出偏移矢量),`μ`(最終輸入平均值矢量)和`σ`(最終輸入標準差矢量)。`μ`和`σ`都是在訓練過程中計算的,但只在訓練后使用(用于替換公式 11-3 中批輸入平均和標準差)。
Ioffe 和 Szegedy 證明,批歸一化大大改善了他們試驗的所有深度神經網絡,極大提高了 ImageNet 分類的效果(ImageNet 是一個圖片分類數據集,用于評估計算機視覺系統)。梯度消失問題大大減少了,他們可以使用飽和激活函數,如 tanh 甚至邏輯激活函數。網絡對權重初始化也不那么敏感。他們能夠使用更大的學習率,顯著加快了學習過程。具體地,他們指出,“應用于最先進的圖像分類模型,批標準減少了 14 倍的訓練步驟實現了相同的精度,以顯著的優勢擊敗了原始模型。[...] 使用批量標準化的網絡集合,我們改進了 ImageNet 分類上的最佳公布結果:達到 4.9% 的前 5 個驗證錯誤(和 4.8% 的測試錯誤),超出了人類評估者的準確性。批量標準化也像一個正則化項一樣,減少了對其他正則化技術的需求(如本章稍后描述的 dropout).
然而,批量標準化的確會增加模型的復雜性(盡管它不需要對輸入數據進行標準化,因為第一個隱藏層會照顧到這一點,只要它是批量標準化的)。 此外,還存在運行時間的損失:由于每層所需的額外計算,神經網絡的預測速度較慢。 但是,可以在訓練之后,處理在 BN 層的前一層,就可以加快速度。方法是更新前一層的權重和偏置項,使其直接輸出合適的縮放值和偏移值。例如,如果前一層計算的是`XW + b`,BN 層計算的是`γ?(XW + b – μ)/σ + β`(忽略了分母中的平滑項`ε`)。如果定義`W′ = γ?W/σ`和`b′ = γ?(b – μ)/σ + β`,公式就能簡化為`XW′ + b′`。因此如果替換前一層的權重和偏置項(`W`和`b`)為`W'`和`b'`,就可以不用 BN 層了(TFLite 的優化器就干了這件事,見第 19 章)。
> 注意:你可能會發現,訓練相當緩慢,這是因為每個周期都因為使用 BN 而延長了時間。但是有了 BN,收斂的速度更快,需要的周期數更少。綜合來看,需要的總時長變短了。
### 使用 Keras 實現批歸一化
和 Keras 大部分功能一樣,實現批歸一化既簡單又直觀。只要每個隱藏層的激活函數前面或后面添加一個`BatchNormalization`層就行,也可以將 BN 層作為模型的第一層。例如,這個模型在每個隱藏層的后面使用了 BN,第一層也用了 BN(在打平輸入之后):
```py
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.BatchNormalization(),
keras.layers.Dense(300, activation="elu", kernel_initializer="he_normal"),
keras.layers.BatchNormalization(),
keras.layers.Dense(100, activation="elu", kernel_initializer="he_normal"),
keras.layers.BatchNormalization(),
keras.layers.Dense(10, activation="softmax")
])
```
這樣就成了!在這個只有兩個隱藏層的例子中,BN 的作用不會那么大,但對于更深的網絡,作用就特別大。
打印一下模型的摘要:
```py
>>> model.summary()
Model: "sequential_3"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
flatten_3 (Flatten) (None, 784) 0
_________________________________________________________________
batch_normalization_v2 (Batc (None, 784) 3136
_________________________________________________________________
dense_50 (Dense) (None, 300) 235500
_________________________________________________________________
batch_normalization_v2_1 (Ba (None, 300) 1200
_________________________________________________________________
dense_51 (Dense) (None, 100) 30100
_________________________________________________________________
batch_normalization_v2_2 (Ba (None, 100) 400
_________________________________________________________________
dense_52 (Dense) (None, 10) 1010
=================================================================
Total params: 271,346
Trainable params: 268,978
Non-trainable params: 2,368
```
可以看到每個 BN 層添加了四個參數:`γ`、 `β`、 `μ` 和 `σ`(例如,第一個 BN 層添加了 3136 個參數,即 4 × 784)。后兩個參數`μ` 和 `σ`是移動平均,不受反向傳播影響,Keras 稱其“不可訓練”(如果將 BN 的總參數 3,136 + 1,200 + 400 除以 2,得到 2368,就是模型中總的不可訓練的參數量)。
看下第一個 BN 層的參數。兩個參數是可訓練的(通過反向傳播),兩個不可訓練:
```py
>>> [(var.name, var.trainable) for var in model.layers[1].variables]
[('batch_normalization_v2/gamma:0', True),
('batch_normalization_v2/beta:0', True),
('batch_normalization_v2/moving_mean:0', False),
('batch_normalization_v2/moving_variance:0', False)]
```
當在 Keras 中創建一個 BN 層時,訓練過程中,還會創建兩個 Keras 在迭代時的操作。該操作會更新移動平均值。因為后端使用的是 TensorFlow,這些操作就是 TensorFlow 操作(第 12 章會討論 TF 操作):
```py
>>> model.layers[1].updates
[<tf.Operation 'cond_2/Identity' type=Identity>,
<tf.Operation 'cond_3/Identity' type=Identity>]
```
BN 的論文作者建議在激活函數之前使用 BN 層,而不是像前面的例子添加到后面。到底是前面還是后面好存在爭議,取決于具體的任務 —— 你最好在數據集上試驗一下哪種選擇好。要在激活函數前添加 BN 層,必須將激活函數從隱藏層拿出來,單獨做成一層。另外,因為 BN 層對每個輸入有一個偏移參數,可以將前一層的偏置項去掉(設置`use_bias=False`):
```py
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.BatchNormalization(),
keras.layers.Dense(300, kernel_initializer="he_normal", use_bias=False),
keras.layers.BatchNormalization(),
keras.layers.Activation("elu"),
keras.layers.Dense(100, kernel_initializer="he_normal", use_bias=False),
keras.layers.BatchNormalization(),
keras.layers.Activation("elu"),
keras.layers.Dense(10, activation="softmax")
])
```
`BatchNormalization`類可供調節的參數不多。默認值通常就可以,但有時需要調節`momentum`,這個超參數是`BatchNormalization`在更新指數移動平均時使用的。給定一個新值`v`(即,一個當前批次的輸入平均或標準差新矢量),BN 層使用下面的等式更新平均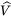:
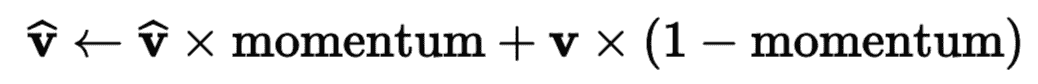
`momentum`的最優值通常接近于 1:比如,0.9、0.99、0.999(大數據的 9 更多,小數據集的 9 少)。
另一個重要的超參數是`axis`:它確定了在哪個軸上歸一。默認是-1,即歸一化最后一個軸(使用其它軸的平均值和標準差)。當輸入是 2D 時(即批的形狀是[`batch size`,`features`]),也就是說每個輸入特征都會根據批次全部實例的平均值和標準差做歸一。例如,前面例子的第一個 BN 層會分別對 784 個輸入特征的每個特征做歸一化(還有縮放和偏移);因此,BN 層會計算 28 個平均值和 28 個標準差(每列 1 個值,根據每行的所有實例計算),用同樣的平均值和標準差歸一化給定列的所有像素。還會有 28 個縮放值和 28 個偏移值。如果仍想對 784 個像素獨立處理,要設置`axis=[1, 2]`。
在訓練和訓練之后,BN 層不會做同樣的計算:BN 會使用訓練中的批次數據和訓練后的最終數據(即移動平均值的最終值)。看看源碼中是如何實現的:
```py
class BatchNormalization(keras.layers.Layer):
[...]
def call(self, inputs, training=None):
[...]
```
`call()`方法具體實現了方法,它有一個參數`training`,默認是 None,但`fit()`方法在訓練中將其設為 1。如果你需要寫一個自定義層,要求自定義層在訓練和測試中的功能不同,就可以在`call()`方法中添加一個參數`training`,用這個參數決定該計算什么(第 12 張會討論自定義層)。
`BatchNormalization`已經成為了深度神經網絡中最常使用的層,以至于計算圖中經常省略,默認嘉定在每個層后面加一個 BN 層。但是 Hongyi Zhang 的一篇文章([https://arxiv.org/abs/1901.09321](https://links.jianshu.com/go?to=https%3A%2F%2Farxiv.org%2Fabs%2F1901.09321))可能改變了這種做法:通過使用一個新的`fixed-update`(fixup)權重初始化方法,作者沒有使用 BN,訓練了一個非常深的神經網絡(多達 10000 層),在復雜圖片分類任務上表現驚艷。但這個結論很新,最好還是再等一等,現在還是使用批歸一化。
### 梯度裁剪
減少梯度爆炸問題的一種常用技術是在反向傳播過程中剪切梯度,使它們不超過某個閾值,這種方法稱為梯度裁剪。梯度裁剪在循環神經網絡中用的很多,因為循環神經網絡中用 BN 很麻煩,參見第 15 章。 對于其它類型的網絡,BN 就足夠了。在 Keras 中,梯度裁剪只需在創建優化器時設置`clipvalue`或`clipnorm`參數,如下:
```py
optimizer = keras.optimizers.SGD(clipvalue=1.0)
model.compile(loss="mse", optimizer=optimizer)
```
優化器會將梯度矢量中的每個值裁剪到-1.0 和 1.0 之間。這意味著損失(對每個可訓練參數)的所有偏導數會被裁剪到-1.0 和 1.0 之間。閾值是一個可以調節的超參數,可能影響到梯度矢量的方向。例如,如果原始梯度矢量是[0.9, 100.0],它大體指向第二個軸;但在裁剪之后變為[0.9, 1.0],方向就大體指向對角線了。在實際中,梯度裁剪的效果不錯。如果想確保梯度裁剪不改變梯度矢量的方向,就需要設置`clipnorm`靠范數裁剪,這樣如果梯度的 l2 范數超過了閾值,就能對整個梯度裁剪。例如,如果設置`clipnorm = 1.0`,矢量[0.9, 100.0]就會被裁剪為[0.00899964, 0.9999595],方向沒變,但第一個量幾乎被抹去了。如果再訓練過程中發現了梯度爆炸(可以用 TensorBoard 跟蹤梯度),最好的方法是既用值也用范數裁剪,設置不同的閾值,看看哪個在驗證集上表現最好。
### 復用預訓練層
從零開始訓練一個非常大的 DNN 通常不是一個好主意,相反,您應該總是嘗試找到一個現有的神經網絡來完成與您正在嘗試解決的任務類似的任務(第 14 章會介紹如何找),然后復用這個網絡的較低層:這就是所謂的遷移學習。這樣不僅能大大加快訓練速度,還將需要更少的訓練數據。
例如,假設你有一個經過訓練的 DNN,能將圖片分為 100 個不同的類別,包括動物,植物,車輛和日常物品。 現在想要訓練一個 DNN 來對特定類型的車輛進行分類。 這些任務非常相似,甚至部分重疊,因此應該嘗試重新使用第一個網絡的一部分(請參見圖 11-4)。
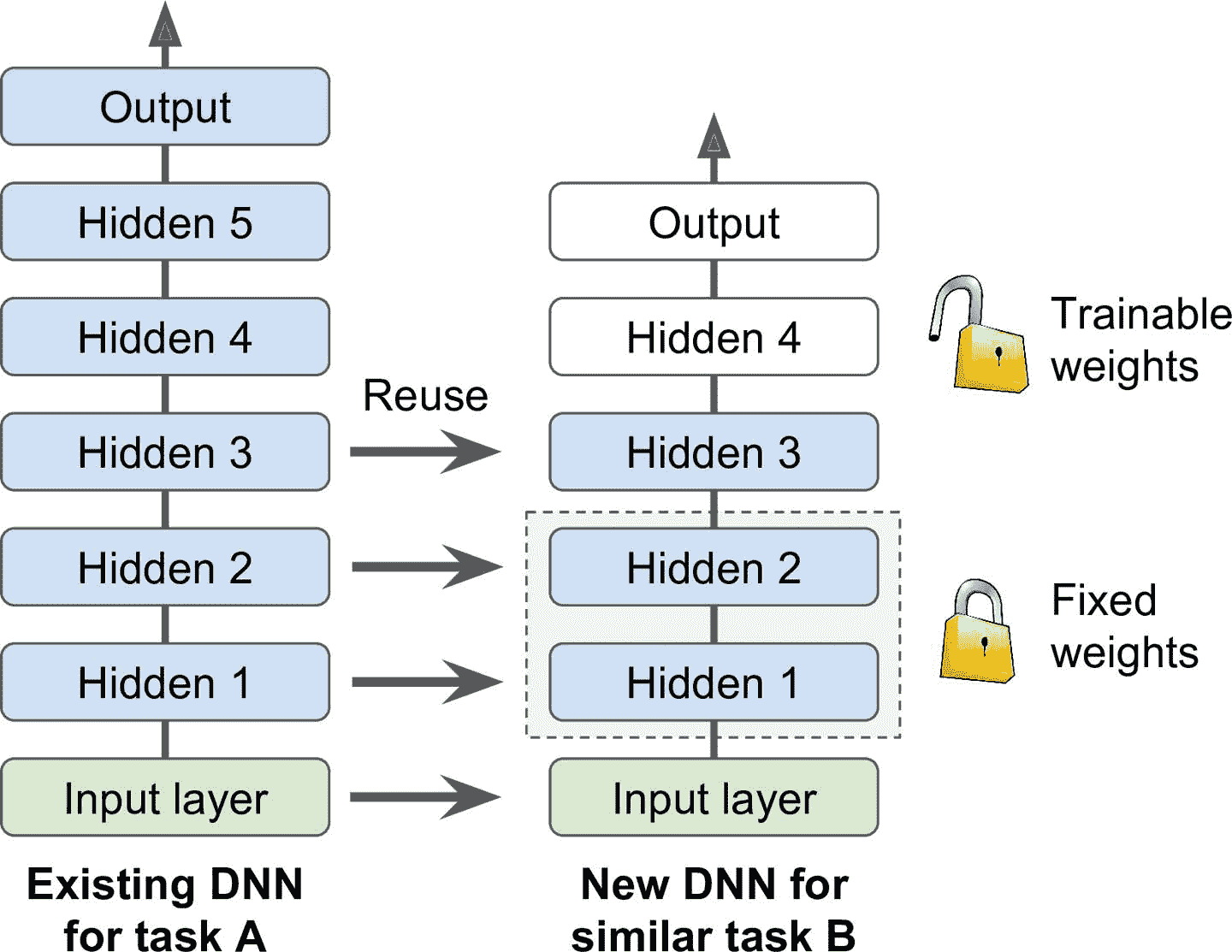圖 11-4 復用預訓練層
> 筆記:如果新任務的輸入圖像與原始任務中使用的輸入圖像的大小不一致,則必須添加預處理步驟以將其大小調整為原始模型的預期大小。 更一般地說,如果輸入具有類似的低級層次的特征,則遷移學習將很好地工作。
原始模型的輸出層通常要替換掉,因為對于新任務可能一點用也沒有,輸出的數量可能就不對。相似的,原始模型的上層也不如淺層管用,因為高階特征可能相差很大。需要確定好到底用幾層。
> 提示:任務越相似,可復用的層越多。對于非常相似的任務,可以嘗試保留所有的吟唱層,替換輸出層。
先將所有復用的層凍結(即,使其權重不可訓練,梯度下降不能修改權重),然后訓練模型,看其表現如何。然后將復用的最上一或兩層解凍,讓反向傳播可以調節它們,再查看性能有無提升。訓練數據越多,可以解凍的層越多。解凍時減小學習率也有幫助,可以避免破壞微調而得的權重。
如果效果不好,或者訓練數據不多,可以嘗試去除頂層,將其余的層都解凍。不斷嘗試,直到找到合適的層,如果訓練數據很多,可以嘗試替換頂層,或者加入更多的隱藏層。
### 用 Keras 進行遷移學習
看一個例子。假設 Fashion MNIST 只有八個類,不包括拖鞋和 T 恤。一些人在這個數據集上搭建并訓練了一個 Keras 模型,且效果不錯(準確率大于 90%),將其稱為模型 A。現在想處理另一個問題:有拖鞋和 T 恤的圖片,要訓練一個二分類器(positive=shirt, negative=sandal)。數據集不大,只有 200 張打了標簽的圖片。當訓練架構與模型 A 相同的新模型時(稱其為模型 B),表現非常好(準確率 97.2%)。但因為這是一個非常簡單的任務(只有兩類),所以準確率應該還可以更高。因為和任務 A 很像,所以可以嘗試一下遷移學習。
首先,加載模型 A,創建一個新模型,除了輸出層不要,保留所有的層:
```py
model_A = keras.models.load_model("my_model_A.h5")
model_B_on_A = keras.models.Sequential(model_A.layers[:-1])
model_B_on_A.add(keras.layers.Dense(1, activation="sigmoid"))
```
`model_A` 和 `model_B_on_A` 公用了一些層。當你訓練`model_B_on_A`時,也會影響`model_A`。如果想避免,需要在復用前克隆`model_A`。要這么做,可以使用`clone.model()`,然后復制權重(`clone.model()`不能克隆權重):
```py
model_A_clone = keras.models.clone_model(model_A)
model_A_clone.set_weights(model_A.get_weights())
```
現在就可以訓練`model_B_on_A`了,但是因為新輸出層是隨機初始化的,誤差較大,較大的誤差梯度可能會破壞復用的權重。為了避免,一種方法是在前幾次周期中,凍結復用的層,讓新層有時間學到合理的權重。要實現的話,將每層的`trainable`屬性設為`False`,然后編譯模型:
```py
for layer in model_B_on_A.layers[:-1]:
layer.trainable = False
model_B_on_A.compile(loss="binary_crossentropy", optimizer="sgd",
metrics=["accuracy"])
```
> 筆記:凍結或解凍模型之后,都需要編譯。
訓練幾個周期之后,就可以解凍復用層(需要再次編譯模型),然后接著訓練以微調模型。解凍之后,最好降低學習率,目的還是避免破壞復用層的權重:
```py
history = model_B_on_A.fit(X_train_B, y_train_B, epochs=4,
validation_data=(X_valid_B, y_valid_B))
for layer in model_B_on_A.layers[:-1]:
layer.trainable = True
optimizer = keras.optimizers.SGD(lr=1e-4) # the default lr is 1e-2
model_B_on_A.compile(loss="binary_crossentropy", optimizer=optimizer,
metrics=["accuracy"])
history = model_B_on_A.fit(X_train_B, y_train_B, epochs=16,
validation_data=(X_valid_B, y_valid_B))
```
最終結果,新模型的測試準確率達到了 99.25%。遷移學習將誤差率從 2.8%降低到了 0.7%,減小了 4 倍!
```py
>>> model_B_on_A.evaluate(X_test_B, y_test_B)
[0.06887910133600235, 0.9925]
```
你相信這個結果嗎?不要相信:因為作者作弊了!作者嘗試了許多方案,才找到一組配置提升了效果。如果你嘗試改變類或隨機種子,就能發現效果下降。作者這里做的是“拷問數據,直到數據招供”。當某篇論文的結果太好了,你應該懷疑下:也許新方法實際沒什么效果(甚至降低了表現),只是作者嘗試了許多變量,只報告了最好的結果(可能只是運氣),踩的坑都沒說。大部分時候,這不是惡意,但確實是科學中許多結果無法復現的原因。作者為什么要作弊呢?因為遷移學習對小網絡幫助不大,小型網絡只能學到幾個模式,緊密網絡學到的具體模式,可能在其他任務中用處不大。遷移學習在深度卷積網絡中表現最好,CNN 學到的特征更通用(特別是淺層)。第 14 章會用剛討論的,回顧遷移學習(下次保證不作弊)。
### 無監督預訓練
假設你想要解決一個復雜的任務,但沒有多少的打了標簽的訓練數據,也找不到一個類似的任務訓練模型。 不要失去希望! 首先,應該嘗試收集更多的有標簽的訓練數據,但是如果做不到,仍然可以進行無監督的訓練(見圖 11-5)。 通常,獲得無標簽的訓練數據成本低,但打標簽成本很高。如果收集了大量無標簽數據,可以嘗試訓練一個無監督模型,比如自編碼器或生成式對抗網絡(見第 17 章)。然后可以復用自編碼器或 GAN 的淺層,加上輸出層,使用監督學習微調網絡(使用標簽數據)。
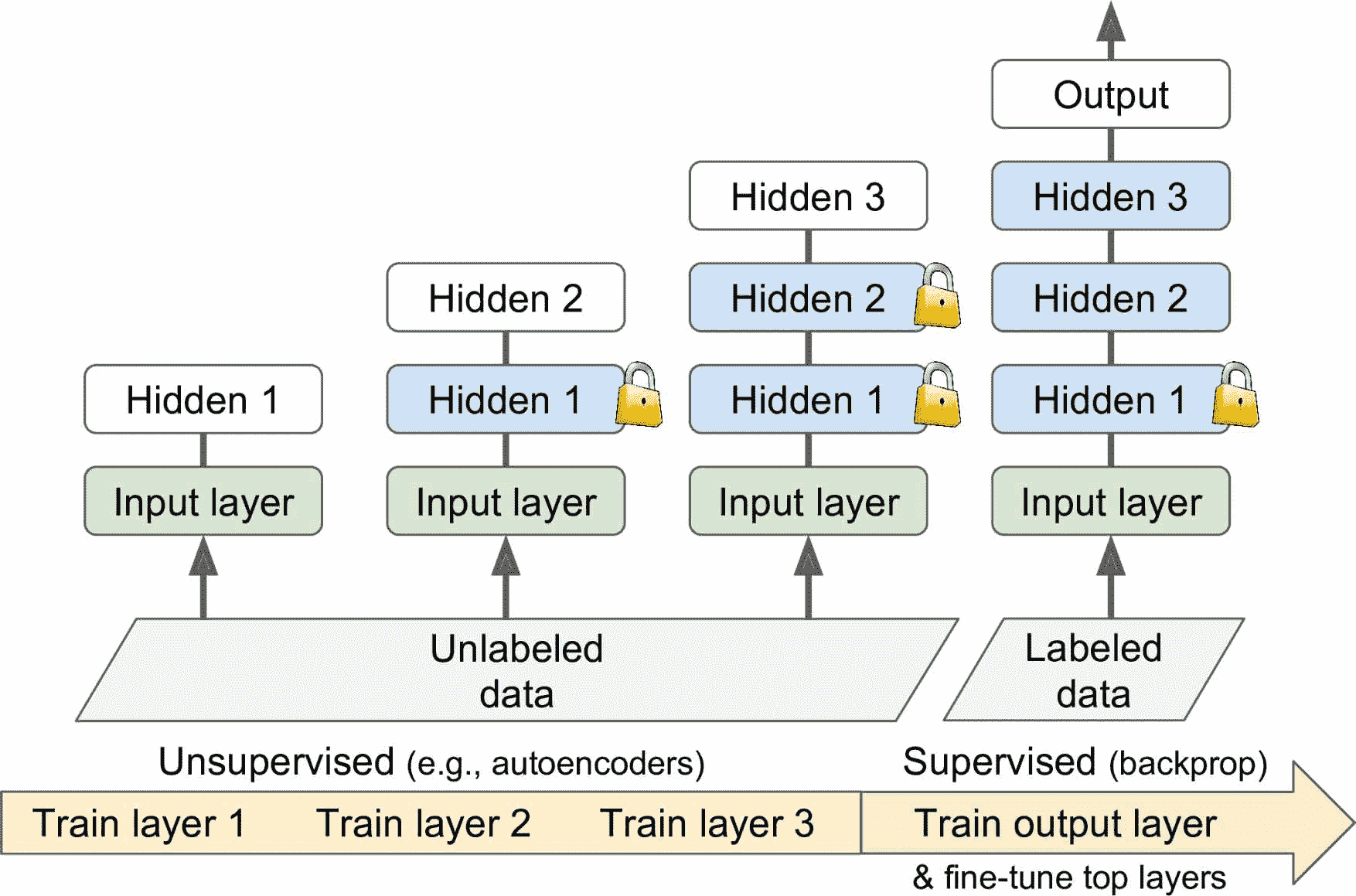圖 11-5 無監督的預訓練
這是 Geoffrey Hinton 和他的團隊在 2006 年使用的技術,導致了神經網絡的復興和深度學習的成功。 直到 2010 年,無監督預訓練(通常使用受限玻爾茲曼機 RBM)是深度網絡的標準,只有在梯度消失問題得到緩解之后,監督訓練 DNN 才更為普遍。 然而,當你有一個復雜的任務需要解決時,沒有類似的模型可以重復使用,而且標記的訓練數據很少,但是大量的未標記的訓練數據時,無監督訓練(現在通常使用自動編碼器、GAN 而不是 RBM)仍然是一個很好的選擇。在深度學習的早期,訓練深度模型很困難,人們使用了一種逐層預訓練的方法(見圖 11-5)。先訓練一個單層無監督模型,通常是 RBM,然后凍結該層,加另一個層,再訓練模型(只訓練新層),然后凍住新層,再加一層,再次訓練模型。現在變得簡單了,直接跳到圖 11-5 中的步驟 3,訓練完整的無監督模型,使用的是自編碼器或 GAN。
### 在輔助任務上預訓練
如果沒有多少標簽訓練數據,最后的選擇是在輔助任務上訓練第一個神經網絡,在輔助任務上可以輕松獲取或生成標簽的訓練數據,然后重新使用該網絡的較低層來完成實際任務。 第一個神經網絡的較低層將學習可能被第二個神經網絡重復使用的特征檢測器。
例如,如果你想建立一個識別面孔的系統,你可能只有幾個人的照片 - 顯然不足以訓練一個好的分類器。 收集每個人的數百張照片將是不實際的。 但是,您可以在互聯網上收集大量隨機人員的照片,并訓練第一個神經網絡來檢測兩張不同的照片是否屬于同一個人。 這樣的網絡將學習面部優秀的特征檢測器,所以重復使用它的較低層將允許你使用很少的訓練數據來訓練一個好的面部分類器。
對于自然語言處理(NLP),可以下載大量文本,然后自動生成標簽數據。例如,可以隨機遮擋一些詞,然后訓練一個模型預測缺失詞。如果能在這個任務上訓練一個表現不錯的模型,則該模型已經在語言層面學到不少了,就可以復用它到實際任務中,再用標簽數據微調(第 15 章會討論更多預訓練任務)。
> 筆記:自監督學習是當你從數據自動生成標簽,然后在標簽數據上使用監督學習訓練模型。因為這種方法無需人工標注,最好將其分類為無監督學習。
## 更快的優化器
訓練一個非常大的深度神經網絡可能會非常緩慢。 到目前為止,我們已經看到了四種加速訓練的方法(并且達到更好性能的方法):對連接權重應用良好的初始化策略,使用良好的激活函數,使用批歸一化以及重用預訓練網絡的部分(使用輔助任務或無監督學習)。 另一個速度提升的方法是使用更快的優化器,而不是常規的梯度下降優化器。 在本節中,我們將介紹最流行的算法:動量優化,Nesterov 加速梯度,AdaGrad,RMSProp,最后是 Adam 和 Nadam 優化。
> 劇透:本節的結論是,幾乎總是應該使用`Adam_optimization`,所以如果不關心它是如何工作的,只需使用`AdamOptimizer`替換`GradientDescentOptimizer`,然后跳到下一節! 只需要這么小的改動,訓練通常會快幾倍。 但是,Adam 優化確實有三個可以調整的超參數(加上學習率)。 默認值通常工作的不錯,但如果您需要調整它們,知道他們怎么實現的可能會有幫助。 Adam 優化結合了來自其他優化算法的幾個想法,所以先看看這些算法是有用的。
## 動量優化
想象一下,一個保齡球在一個光滑的表面上平緩的斜坡上滾動:它會緩慢地開始,但是它會很快地達到最終的速度(如果有一些摩擦或空氣阻力的話)。 這是 Boris Polyak 在 1964 年提出的動量優化背后的一個非常簡單的想法。相比之下,普通的梯度下降只需要沿著斜坡進行小的有規律的下降步驟,所以需要更多的時間才能到達底部。
回想一下,梯度下降只是通過直接減去損失函數`J(θ)`相對于權重`θ`的梯度(`?θJ(θ)`),乘以學習率`η`來更新權重`θ`。 等式是:θ ← θ – η?<sub>θ</sub>J(θ)。它不關心早期的梯度是什么。 如果局部梯度很小,則會非常緩慢。
動量優化很關心以前的梯度:在每次迭代時,它將動量矢量`m`(乘以學習率`η`)與局部梯度相加,并且通過簡單地減去該動量矢量來更新權重(參見公式 11-4)。 換句話說,梯度用作加速度,不用作速度。 為了模擬某種摩擦機制,避免動量過大,該算法引入了一個新的超參數`β`,簡稱為動量,它必須設置在 0(高摩擦)和 1(無摩擦)之間。 典型的動量值是 0.9。
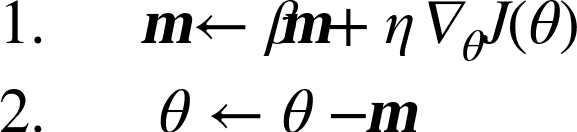公式 11-4 動量算法
可以很容易驗證,如果梯度保持不變,則最終速度(即,權重更新的最大大小)等于該梯度乘以學習率`η`乘以`1/(1-β)`。 例如,如果`β = 0.9`,則最終速度等于學習率的梯度乘以 10 倍,因此動量優化比梯度下降快 10 倍! 這使動量優化比梯度下降快得多。 特別是,我們在第四章中看到,當輸入量具有非常不同的尺度時,損失函數看起來像一個細長的碗(見圖 4-7)。 梯度下降速度很快,但要花很長的時間才能到達底部。 相反,動量優化會越來越快地滾下山谷底部,直到達到底部(最佳)。在不使用批歸一化的深度神經網絡中,較高層往往會得到具有不同的尺度的輸入,所以使用動量優化會有很大的幫助。 它也可以幫助滾過局部最優值。
> 筆記:由于動量的原因,優化器可能會超調一些,然后再回來,再次超調,并在穩定在最小值之前多次振蕩。 這就是為什么在系統中有一點摩擦的原因之一:它消除了這些振蕩,從而加速了收斂。
在 Keras 中實現動量優化很簡單:只需使用`SGD`優化器,設置`momentum`超參數,然后就可以躺下賺錢了!
```py
optimizer = keras.optimizers.SGD(lr=0.001, momentum=0.9)
```
動量優化的一個缺點是它增加了另一個超參數來調整。 然而,0.9 的動量值通常在實踐中運行良好,幾乎總是比梯度下降快。
### Nesterov 加速梯度
Yurii Nesterov 在 1983 年提出的動量優化的一個小變體幾乎總是比普通的動量優化更快。 Nesterov 動量優化或 Nesterov 加速梯度(Nesterov Accelerated Gradient,NAG)的思想是測量損失函數的梯度不是在局部位置,而是在動量方向稍微靠前(見公式 11-5)。 與普通的動量優化的唯一區別在于梯度是在`θ+βm`而不是在`θ`處測量的。
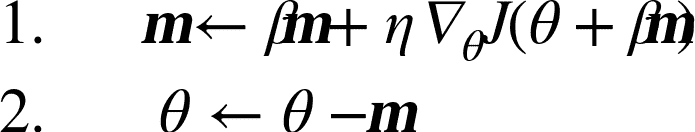公式 11-5 Nesterov 加速梯度算法
這個小小的調整是可行的,因為一般來說,動量矢量將指向正確的方向(即朝向最優方向),所以使用在該方向上測得的梯度稍微更精確,而不是使用 原始位置的梯度,如圖 11-6 所示(其中`?1`代表在起點`θ`處測量的損失函數的梯度,`?2`代表位于`θ+βm`的點處的梯度)。
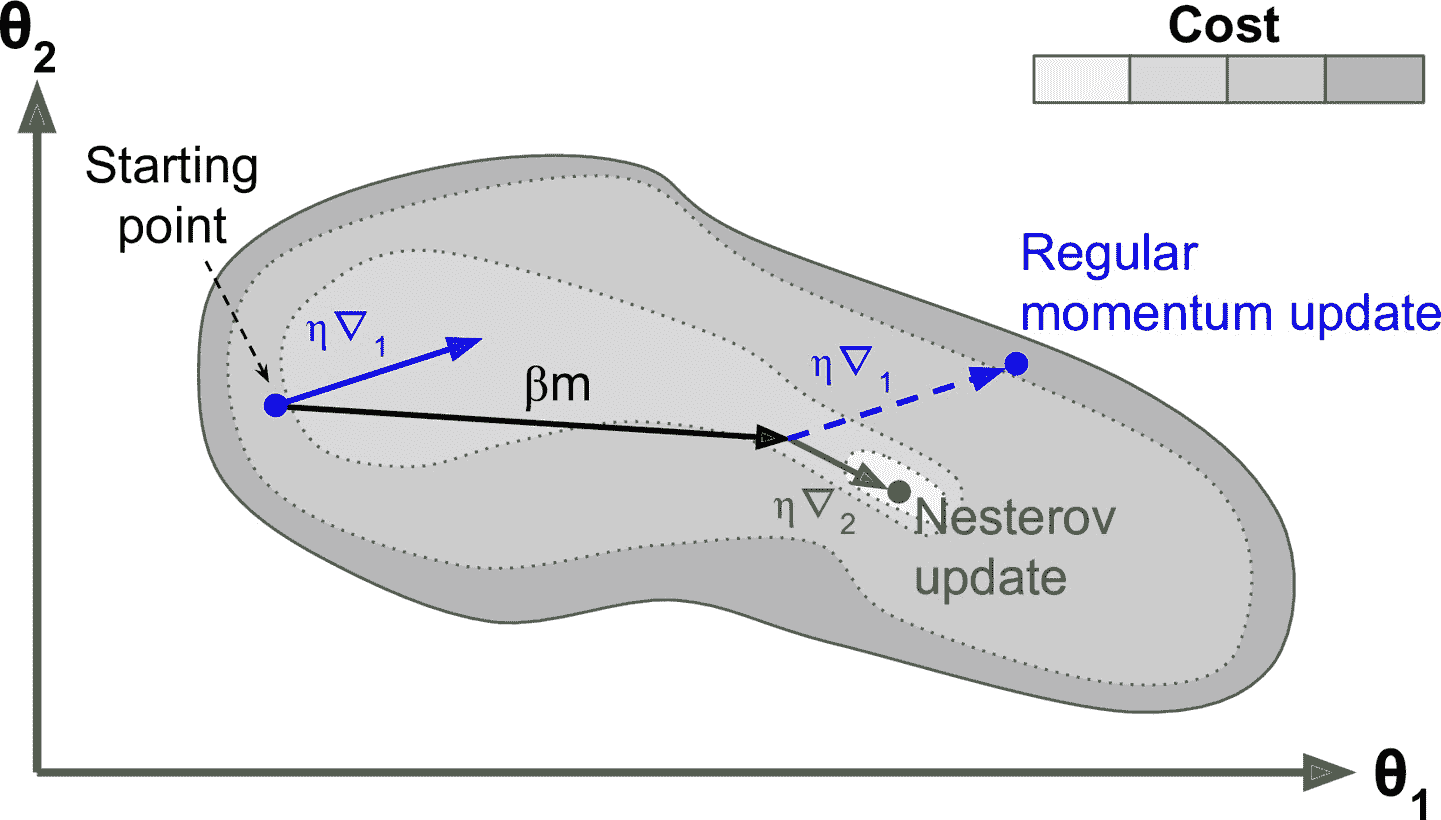圖 11-6 常規 vsNesterov 動量優化
可以看到,Nesterov 更新稍微靠近最佳值。 過了一段時間,這些小的改進加起來,NAG 最終比常規的動量優化快得多。 此外,當動量推動權重橫跨山谷時,▽1 繼續推進越過山谷,而▽2 推回山谷的底部。 這有助于減少振蕩,從而更快地收斂。
與常規的動量優化相比,NAG 幾乎總能加速訓練。 要使用它,只需在創建`SGD`時設置`nesterov=True:
```py
optimizer = keras.optimizers.SGD(lr=0.001, momentum=0.9, nesterov=True)
```
### AdaGrad
再次考慮細長碗的問題:梯度下降從最陡峭的斜坡快速下降,然后緩慢地下到谷底。 如果算法能夠早期檢測到這個問題并且糾正它的方向來指向全局最優點,那將是非常好的。AdaGrad 算法通過沿著最陡的維度縮小梯度向量來實現這一點(見公式 11-6):
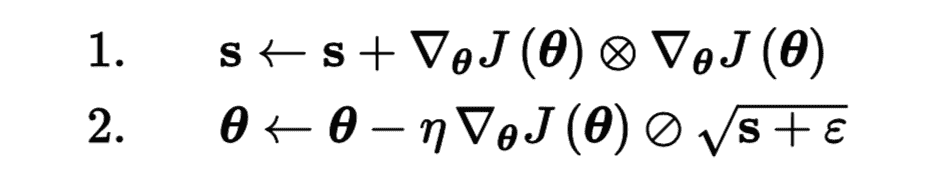公式 11-6 AdaGrad 算法
第一步將梯度的平方累加到矢量`s`中(?符號表示元素級別相乘)。 這個向量化形式相當于向量`s`的每個元素`si`計算 s<sub>i</sub> ← s<sub>i</sub> + (? / ? θ<sub>i</sub> J(θ))<sup>2</sup>。換一種說法,每個 s<sub>i</sub> 累加損失函數對參數θ<sub>i</sub>的偏導數的平方。 如果損失函數沿著第`i`維陡峭,則在每次迭代時, s<sub>i</sub> 將變得越來越大。
第二步幾乎與梯度下降相同,但有一個很大的不同:梯度矢量按比例(s+ε)^0.5 縮小 (?符號表示元素分割,`ε`是避免被零除的平滑項,通常設置為 10<sup>-10</sup>。 這個矢量化的形式相當于所有θ<sub>i</sub>同時計算
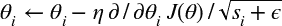
簡而言之,這種算法會降低學習速度,但對于陡峭的維度,其速度要快于具有溫和的斜率的維度。 這被稱為自適應學習率。 它有助于將更新的結果更直接地指向全局最優(見圖 11-7)。 另一個好處是它不需要那么多的去調整學習率超參數`η`。
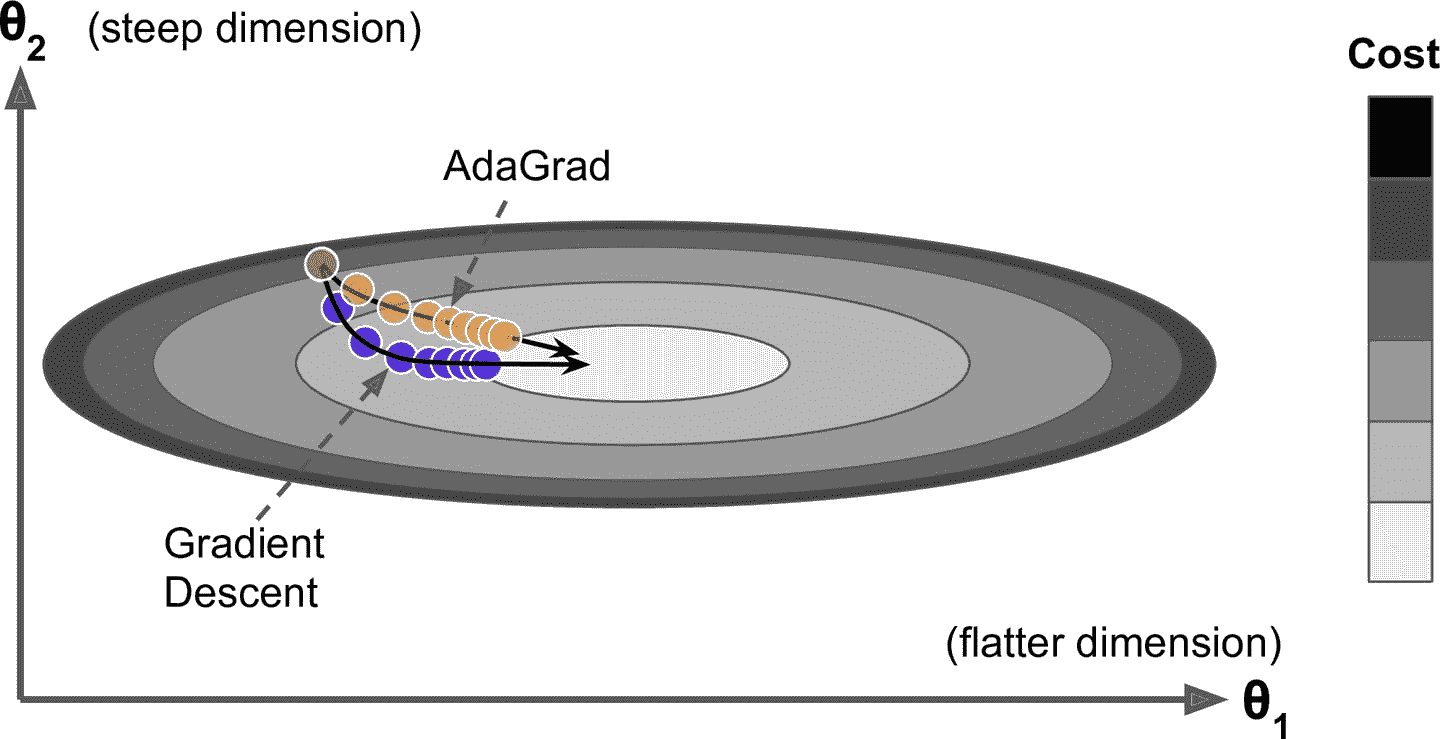圖 11-7 AdaGard vs 梯度下降
對于簡單的二次問題,AdaGrad 經常表現良好,但不幸的是,在訓練神經網絡時,它經常停止得太早。 學習率被縮減得太多,以至于在達到全局最優之前,算法完全停止。 所以,即使 Keras 有一個`Adagrad` 優化器,你也不應該用它來訓練深度神經網絡(雖然對線性回歸這樣簡單的任務可能是有效的)。但是,理解 AdaGrad 對掌握其它自適應學習率還是很有幫助的。
### RMSProp
前面看到,AdaGrad 的風險是降速太快,可能無法收斂到全局最優。RMSProp 算法通過僅累積最近迭代(而不是從訓練開始以來的所有梯度)的梯度來修正這個問題。 它通過在第一步中使用指數衰減來實現(見公式 11-7)。
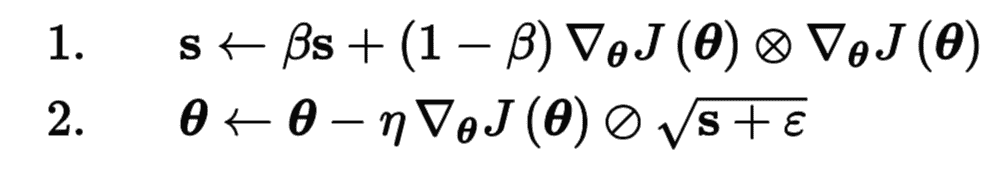公式 11-7 RMSProp 算法
它的衰變率`β`通常設定為 0.9。 是的,它又是一個新的超參數,但是這個默認值通常運行良好,所以你可能根本不需要調整它。
正如所料,Keras 擁有一個`RMSProp`優化器:
```py
optimizer = keras.optimizers.RMSprop(lr=0.001, rho=0.9)
```
除了非常簡單的問題,這個優化器幾乎總是比 AdaGrad 執行得更好。 它通常也比動量優化和 Nesterov 加速梯度表現更好。 事實上,這是許多研究人員首選的優化算法,直到 Adam 優化出現。
## Adam 和 Nadam 優化
Adam,代表自適應矩估計,結合了動量優化和 RMSProp 的思想:就像動量優化一樣,它追蹤過去梯度的指數衰減平均值,就像 RMSProp 一樣,它跟蹤過去平方梯度的指數衰減平均值 (見方程式 11-8)。
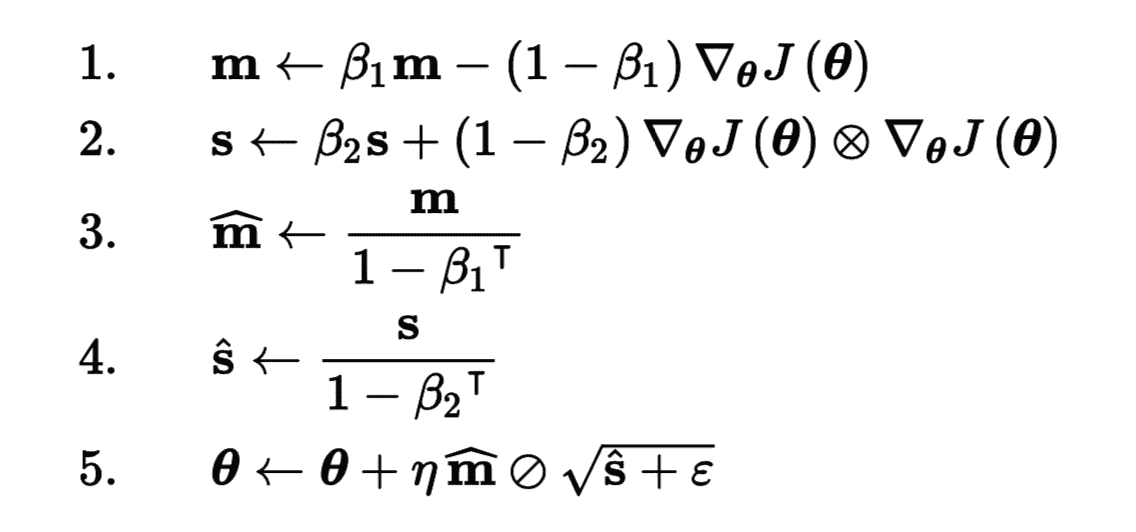公式 11-8 Adam 算法
T 代表迭代次數(從 1 開始)。
如果你只看步驟 1, 2 和 5,你會注意到 Adam 與動量優化和 RMSProp 的相似性。 唯一的區別是第 1 步計算指數衰減的平均值,而不是指數衰減的和,但除了一個常數因子(衰減平均值只是衰減和的`1 - β1`倍)之外,它們實際上是等效的。 步驟 3 和步驟 4 是一個技術細節:由于`m`和`s`初始化為 0,所以在訓練開始時它們會偏向 0,所以這兩步將在訓練開始時幫助提高`m`和`s`。
動量衰減超參數`β1`通常初始化為 0.9,而縮放衰減超參數`β2`通常初始化為 0.999。 如前所述,平滑項`ε`通常被初始化為一個很小的數,例如 10<sup>-7</sup>。這些是 TensorFlow 的`Adam`類的默認值(更具體地,ε默認為 None,Keras 將使用`keras.backend.epsilon()`,默認為 10<sup>-7</sup>,可以通過`keras.backend.set_epsilon()`更改),所以你可以簡單地使用:
```py
optimizer = keras.optimizers.Adam(lr=0.001, beta_1=0.9, beta_2=0.999)
```
實際上,由于 Adam 是一種自適應學習率算法(如 AdaGrad 和 RMSProp),所以對學習率超參數`η`的調整較少。 您經常可以使用默認值`η= 0.001`,使 Adam 相對于梯度下降更容易使用。
> 提示:如果讀者對這些不同的技術感到頭暈腦脹,不用擔心,本章末尾會提供一些指導。
最后,Adam 還有兩種變體值得一看:
AdaMax
公式 11-8 的第 2 步中,Adam 積累了`s`的梯度平方(越近,權重越高)。第 5 步中,如果忽略了ε、第 3 步和第 4 步(只是技術細節而已),Adam 是通過`s`的平方根更新參數。總之,Adam 通過時間損耗梯度的 l2 范數更新參數(l2 范數是平方和的平方根)。AdaMax(也是在 Adam 的同一篇論文中介紹的)用?∞范數(max 的另一種說法)代替了?2 范數。更具體的,是在第 2 步中做了替換,舍棄了第 4 步,第 5 步中用`s`(即時間損耗的最大值)更新梯度。在實踐中,這樣可以使 AdaMax 比 Adam 更穩定,但也要取決于數據集,總體上,Adam 表現更好。因此,AdaMax 只是 Adam 碰到問題時的另一種選擇。
Nadam
Nadam 優化是 Adam 優化加上了 Nesterov 技巧,所以通常比 Adam 收斂的快一點。在論文([http://cs229.stanford.edu/proj2015/054_report.pdf](https://links.jianshu.com/go?to=http%3A%2F%2Fcs229.stanford.edu%2Fproj2015%2F054_report.pdf))中,作者 Timothy Dozat 在不同任務上試驗了不同的優化器,發現 Nadam 通常比 Adam 效果好,但有時不如 RMSProp。
> 警告:自適應優化方法(包括 RMSProp,Adam,Nadam)總體不錯,收斂更快。但是 Ashia C. Wilson 在 2017 年的一篇論文([https://arxiv.org/abs/1705.08292](https://links.jianshu.com/go?to=https%3A%2F%2Farxiv.org%2Fabs%2F1705.08292))中說,這些自適應優化方法在有些數據集上泛化很差。所以當你對模型失望時,可以嘗試下普通的 Nesterov 加速梯度:你的數據集可能只是對自適應梯度敏感。另外要調研最新的研究進展,因為這個領域進展很快。
目前所有討論的優化方法都是基于一階偏導(雅可比矩陣)的。文獻中還介紹了基于二階導數(黑森矩陣,黑森矩陣是雅可比矩陣的騙到)的算法。但是,后者很難應用于深度神經網絡,因為每個輸出有 n<sup>2</sup>個黑森矩陣(n 是參數個數),每個輸出只有 n 個雅可比矩陣。因為 DNN 通常有數萬個參數,二階優化器通常超出了內存,就算內存能裝下,計算黑森矩陣也非常慢。
> 訓練稀疏模型
> 所有剛剛提出的優化算法都會產生緊密模型,這意味著大多數參數都是非零的。 如果你在運行時需要一個非常快的模型,或者如果你需要它占用較少的內存,你可能更喜歡用一個稀疏模型來代替。
> 實現這一點的一個微不足道的方法是像平常一樣訓練模型,然后丟掉微小的權重(將它們設置為 0)。但這通常不會生成一個稀疏的模型,而且可能使模型性能下降。
> 更好的選擇是在訓練過程中應用強 ?1 正則化,因為它會推動優化器盡可能多地消除權重(如第 4 章關于 Lasso 回歸的討論)。
> 如果這些技術可能仍然不成,就查看[TensorFlow Model Optimization Toolkit (TF-MOT)](https://links.jianshu.com/go?to=https%3A%2F%2Fhoml.info%2Ftfmot),它提供了一些剪枝 API,可以在訓練中根據量級迭代去除權重。
表 11-2 比較了討論過的優化器(*是差,**是平均,***是好)。
表 11-2 優化器比較
### 學習率調整
找到一個好的學習速率非常重要。 如果設置太高,訓練時可能離散。如果設置得太低,訓練最終會收斂到最佳狀態,但會花費很長時間。 如果將其設置得稍高,開始的進度會非常快,但最終會在最優解周圍跳動,永遠不會停下來。如果計算資源有限,可能需要打斷訓練,在最優收斂之前拿到一個次優解(見圖 11-8)。
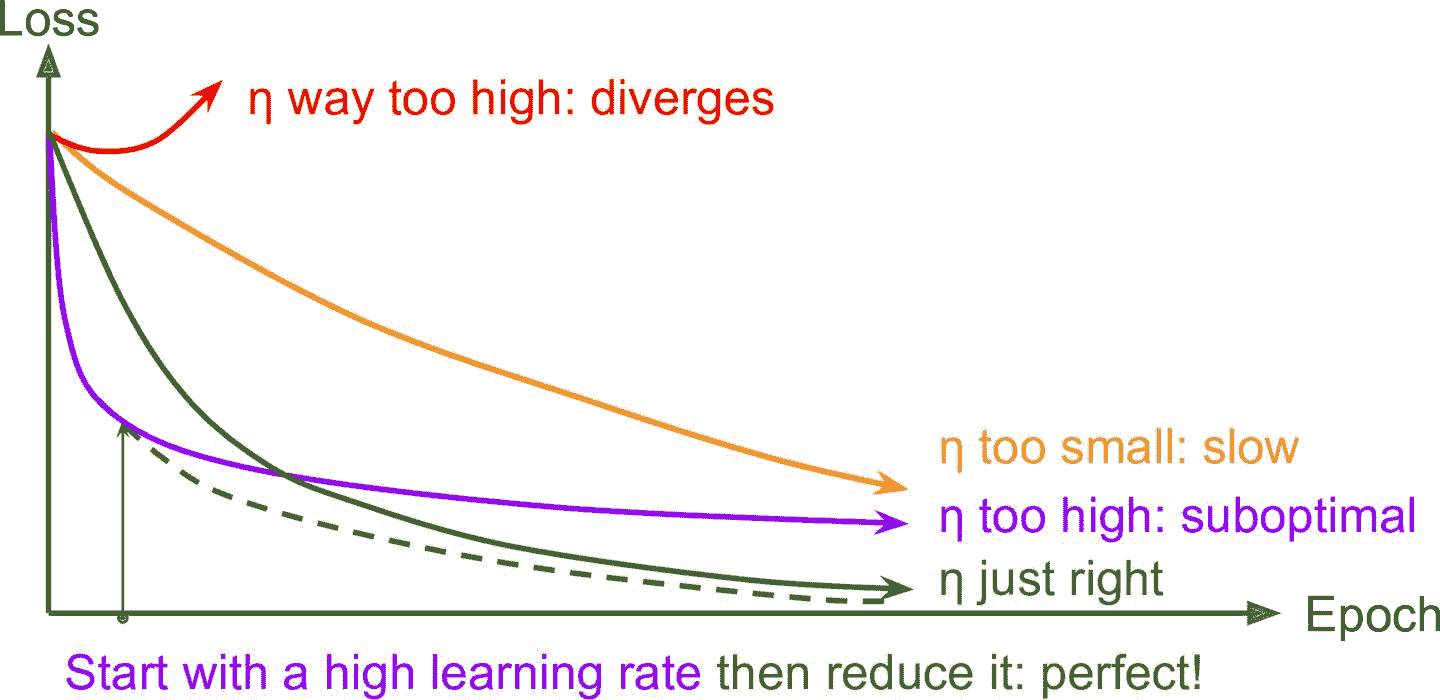圖 11-8 不同學習速率的學習曲線
正如第 10 章討論過的,可以通過幾百次迭代找到一個好的學習率,學習率一開始設的很小,然后指數級提高,查看學習曲線,找到那條要要開始抬高的曲線,要找的學習率比這條曲線稍低。
但除了固定學習率,還有更好的方法:如果你從一個高的學習率開始,然后一旦它停止快速的進步就減少它,你可以比最佳的恒定學習率更快地達到一個好的解決方案。 有許多不同的策略,以減少訓練期間的學習率。 這些策略被稱為學習率調整(我們在第 4 章中簡要介紹了這個概念),其中最常見的是:
冪調度:
設學習率為迭代次數 t 的函數: η(t) = η<sub>0</sub> (1 + t/s)<sup>c</sup>。初始學習率η<sub>0</sub>, 冪`c`(通常被設置為 1),步數`s`是超參數。學習率在每步都會下降,s 步后,下降到η<sub>0</sub> / 2。再經過 s 步,下降到η<sub>0</sub> / 3,然后是η<sub>0</sub> / 4、η<sub>0</sub> / 5,以此類推。可以看到,策略是一開始很快,然后越來越慢。冪調度需要調節η<sub>0</sub>和 s(也可能有 c)。
指數調度:
將學習率設置為迭代次數`t`的函數:η(t) = η<sub>0</sub> 0.1<sup>t/s</sup>。 學習率每步都會下降 10 倍。冪調度的下降是越來越慢,指數調度保持 10 倍不變。
預定的分段恒定學習率:
先在幾個周期內使用固定的學習率(比如 5 個周期內學習率設置為 η<sub>0</sub> = 0.1),然后在另一個周期內設更小的學習率(比如 50 個周期η<sub>1</sub> = 0.001),以此類推。雖然這個解決方案可以很好地工作,但是通常需要弄清楚正確的學習速度順序以及使用時長。
性能調度:
每 N 步測量驗證誤差(就像提前停止一樣),當誤差下降時,將學習率降低`λ`倍。
1 循環調度:
與其它方法相反,1 循環調度(Leslie Smith 在 2018 年提出)一開始在前半個周期將學習率η<sub>0</sub> 線性增加到η<sub>1</sub>,然后在后半個周期內再線性下降到η<sub>0</sub>,最后幾個周期學習率下降幾個數量級(仍然是線性的)。用前面的方法找到最優學習率的方法確定η<sub>1</sub>,η<sub>0</sub>是η<sub>1</sub>的十分之一。當使用動量時,先用一個高動量(比如 0.95),然后在訓練上半段下降(比如線性下降到 0.85),然后在訓練后半部分上升到最高值(0.95),最后幾個周期也用最高值完成。Smith 做了許多試驗,證明這個方法可以顯著加速并能提高性能。例如,在 CIFAR10 圖片數據集上,這個方法在 100 個周期就達到了 91.9%的驗證準確率,而標準方法經過 800 個周期才打到 90.3%(模型架構不變)。
Andrew Senior 等人在 2013 年的論文比較了使用動量優化訓練深度神經網絡進行語音識別時一些最流行的學習率調整的性能。 作者得出結論:在這種情況下,性能調度和指數調度都表現良好,但他們更喜歡指數調度,因為它實現起來比較簡單,容易調整,收斂速度略快于最佳解決方案。作者還之處,1 周期表現更好。
使用 Keras 實現學習率冪調整非常簡單,只要在優化器中設定`decay`超參數:
```py
optimizer = keras.optimizers.SGD(lr=0.01, decay=1e-4)
```
`decay`是`s`(更新學習率的步驟數),Keras 假定`c`等于 1。
指數調度和分段恒定學習率也很簡單。首先定義一個函數接受當前周期,然后返回學習率。例如,如下實現指數調度:
```py
def exponential_decay_fn(epoch):
return 0.01 * 0.1**(epoch / 20)
```
如果不想硬實現η<sub>0</sub>和 s,可以實現一個函數返回配置函數:
```py
def exponential_decay(lr0, s):
def exponential_decay_fn(epoch):
return lr0 * 0.1**(epoch / s)
return exponential_decay_fn
exponential_decay_fn = exponential_decay(lr0=0.01, s=20)
```
然后,創建一個`LearningRateScheduler`調回,給它一個調度函數,然后將調回傳遞給`fit()`:
```py
lr_scheduler = keras.callbacks.LearningRateScheduler(exponential_decay_fn)
history = model.fit(X_train_scaled, y_train, [...], callbacks=[lr_scheduler])
```
`LearningRateScheduler`會在每個周期開始時更新優化器的`learning_rate`屬性。每個周期更新一次學習率就夠了,但如果想更新更頻繁,例如每步都更新,可以通過寫調回實現(看前面指數調回的例子)。如果每個周期有許多步,每步都更新學習率是非常合理的。或者,可以使用`keras.optimizers.schedules`方法。
調度函數可以將當前學習率作為第二個參數。例如,下面的調度函數將之前的學習率乘以 0.1<sup>1/20</sup>,同樣實現了指數下降:
```py
def exponential_decay_fn(epoch, lr):
return lr * 0.1**(1 / 20)
```
該實現依靠優化器的初始學習率(與前面的實現相反),所以一定要設置對。
當保存模型時,優化器和學習率也能保存。這意味著,只要有這個新的調度函數,就能加載模型接著訓練。如果調度函數使用了周期,會稍微麻煩點:周期不會保存,每次調用`fit()`方法時,周期都會重置為 0。如果加載模型接著訓練,可能會導致學習率很大,會破壞模型的權重。一種應對方法是手動設置`fit()`方法的參數`initial_epoch`,是周期從正確的值開始。
對于分段恒定學習率調度,可以使用如下的調度函數,然后創建一個`LearningRateScheduler`調回,傳遞給`fit()`方法:
```py
def piecewise_constant_fn(epoch):
if epoch < 5:
return 0.01
elif epoch < 15:
return 0.005
else:
return 0.001
```
對于性能調度,使用`ReduceLROnPlateau`調回。例如,如果將下面的調回去傳遞給`fit()`,只要驗證損失在連續 5 個周期內沒有改進,就會將學習率乘以 0.5:
```py
lr_scheduler = keras.callbacks.ReduceLROnPlateau(factor=0.5, patience=5)
```
最后,tf.keras 還提供了一種實現學習率調度的方法:使用`keras.optimizers.schedules`中一種可用的調度定義學習率。這樣可以在每步更新學習率。例如,還可以如下實現前面的函數`exponential_decay_fn()`:
```py
s = 20 * len(X_train) // 32 # number of steps in 20 epochs (batch size = 32)
learning_rate = keras.optimizers.schedules.ExponentialDecay(0.01, s, 0.1)
optimizer = keras.optimizers.SGD(learning_rate)
```
這樣又好看又簡單,另外當保存模型時,學習率和調度(包括狀態)也能保存。但是這個方法不屬于 Keras API,是 tf.keras 專有的。
對于 1 循環調度,實現也不困難:只需創建一個在每個迭代修改學習率的自定義調回(通過更改`self.model.optimizer.lr`更新學習率)。代碼見 Jupyter Notebook 的例子。
總結一下,指數調度、性能調度和 1 循環調度可以極大加快收斂,不妨一試!
## 通過正則化避免過擬合
有四個參數,我可以擬合一個大象,五個我可以讓他擺動他的象鼻。—— John von Neumann,cited by Enrico Fermi in Nature 427
有數千個參數,甚至可以擬合整個動物園。深度神經網絡通常具有數以萬計的參數,有時甚至是數百萬。 有了這么多的參數,網絡擁有難以置信的自由度,可以適應各種復雜的數據集。 但是這個很大的靈活性也意味著它很容易過擬合訓練集。所以需要正則。第 10 章用過了最好的正則方法之一:早停。另外,雖然批歸一化是用來解決梯度不穩定的,但也可以作為正則器。這一節會介紹其它一些最流行的神經網絡正則化技術:?1 和 ?2 正則、dropout 和最大范數正則。
### ?1 和 ?2 正則
就像第 4 章中對簡單線性模型所做的那樣,可以使用 ?2 正則約束一個神經網絡的連接權重,或?1 正則得到稀疏模型(許多權重為 0)。下面是對 Keras 的連接權重設置?2 正則,正則因子是 0.01:
```py
layer = keras.layers.Dense(100, activation="elu",
kernel_initializer="he_normal",
kernel_regularizer=keras.regularizers.l2(0.01))
```
`l2`函數返回的正則器會在訓練中的每步被調用,以計算正則損失。正則損失隨后被添加到最終損失。如果要使用?1 正則,可以使用`keras.regularizers.l1()`;如果想使用?1 和 ?2 正則,可以使用`keras.regularizers.l1_l2()`(要設置兩個正則因子)。
因為想對模型中的所有層使用相同的正則器,還要使用相同的激活函數和相同的初始化策略。參數重復使代碼很難看。為了好看,可以用循環重構代碼。另一種方法是使用 Python 的函數`functools.partial()`,它可以為任意可調回對象創建封裝類,并有默認參數值:
```py
from functools import partial
RegularizedDense = partial(keras.layers.Dense,
activation="elu",
kernel_initializer="he_normal",
kernel_regularizer=keras.regularizers.l2(0.01))
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
RegularizedDense(300),
RegularizedDense(100),
RegularizedDense(10, activation="softmax",
kernel_initializer="glorot_uniform")
])
```
### Dropout
dropout 是深度神經網絡最流行的正則化方法之一。 它由 Geoffrey Hinton 于 2012 年提出,并在 Nitish Srivastava 等人的 2014 年論文中進一步詳細描述,并且已被證明是非常成功的:即使是最先進的神經網絡,僅僅通過增加 dropout 就可以提高 1-2%的準確度。 這聽起來可能不是很多,但是當一個模型已經具有 95% 的準確率時,獲得 2% 的準確度提升意味著將誤差率降低近 40%(從 5% 誤差降至大約 3%)。
這是一個相當簡單的算法:在每個訓練步驟中,每個神經元(包括輸入神經元,但不包括輸出神經元)都有一個暫時“丟棄”的概率`p`,這意味著在這個訓練步驟中它將被完全忽略, 在下一步可能會激活(見圖 11-9)。 超參數`p`稱為丟失率,通常設為 10%到 50%之間;循環神經網絡之間接近 20-30%,在卷積網絡中接近 40-50%。 訓練后,神經元不會再丟失。 這就是全部(除了我們將要討論的技術細節)。
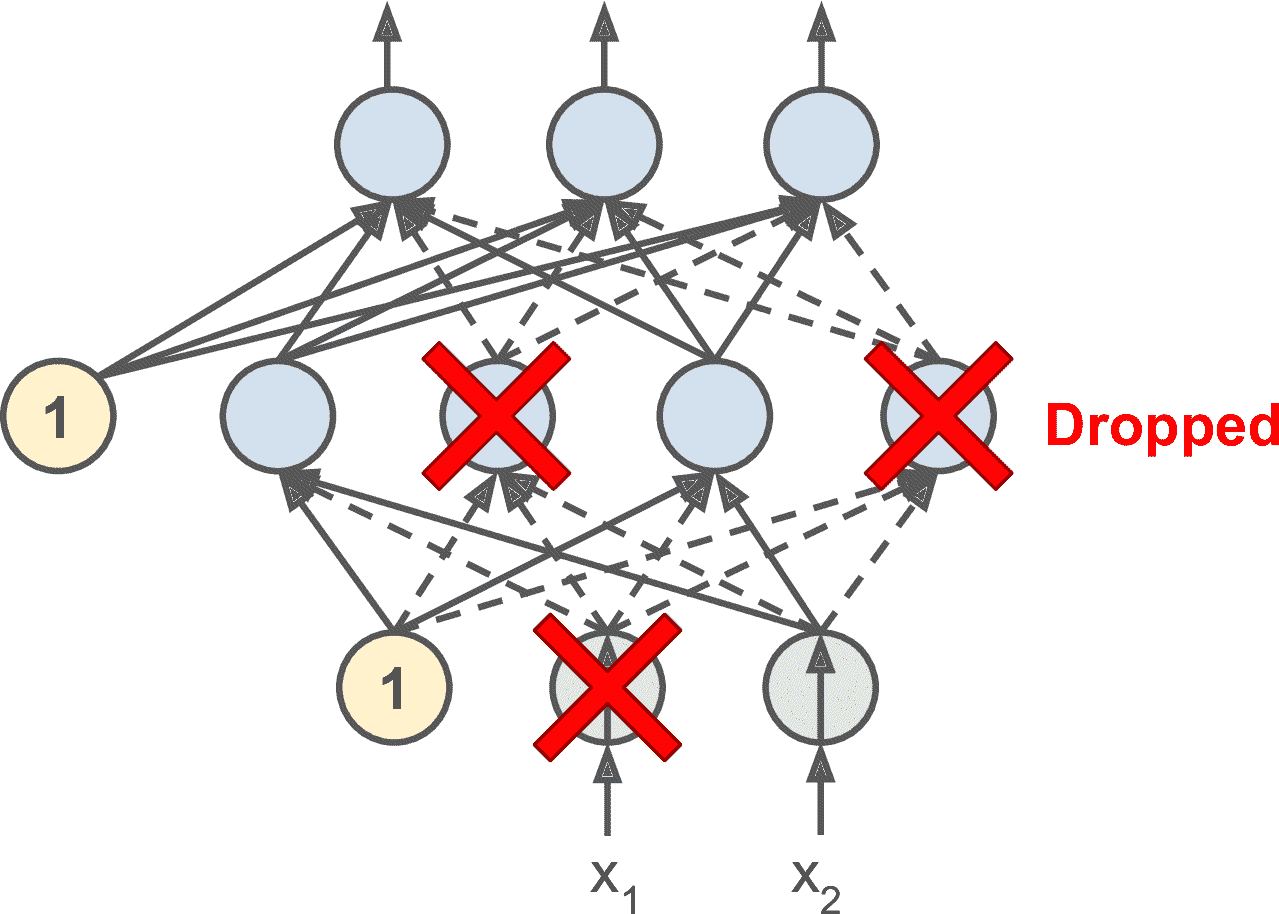圖 11-9 丟失正則化
這個具有破壞性的方法竟然行得通,這是相當令人驚訝的。如果一個公司的員工每天早上被告知要擲硬幣來決定是否上班,公司的表現會不會更好呢?那么,誰知道;也許會!公司顯然將被迫適應這樣的組織構架;它不能依靠任何一個人操作咖啡機或執行任何其他關鍵任務,所以這個專業知識將不得不分散在幾個人身上。員工必須學會與其他的許多同事合作,而不僅僅是其中的一小部分。該公司將變得更有彈性。如果一個人離開了,并沒有什么區別。目前還不清楚這個想法是否真的可以在公司實行,但它確實對于神經網絡是可行的。神經元被 dropout 訓練不能與其相鄰的神經元共適應;他們必須盡可能讓自己變得有用。他們也不能過分依賴一些輸入神經元;他們必須注意他們的每個輸入神經元。他們最終對輸入的微小變化會不太敏感。最后,你會得到一個更穩定的網絡,泛化能力更強。
了解 dropout 的另一種方法是認識到每個訓練步驟都會產生一個獨特的神經網絡。 由于每個神經元可以存在或不存在,總共有`2 ^ N`個可能的網絡(其中 N 是可丟棄神經元的總數)。 這是一個巨大的數字,實際上不可能對同一個神經網絡進行兩次采樣。 一旦你運行了 10,000 個訓練步驟,你基本上已經訓練了 10,000 個不同的神經網絡(每個神經網絡只有一個訓練實例)。 這些神經網絡顯然不是獨立的,因為它們共享許多權重,但是它們都是不同的。 由此產生的神經網絡可以看作是所有這些較小的神經網絡的平均集成。
> 提示:在實際中,可以只將 dropout 應用到最上面的一到三層(包括輸出層)。
有一個小而重要的技術細節。 假設`p = 50%`,在這種情況下,在測試期間,在訓練期間神經元將被連接到兩倍于(平均)的輸入神經元。 為了彌補這個事實,我們需要在訓練之后將每個神經元的輸入連接權重乘以 0.5。 如果我們不這樣做,每個神經元的總輸入信號大概是網絡訓練的兩倍,這不太可能表現良好。 更一般地說,我們需要將每個輸入連接權重乘以訓練后的保持概率(`1-p`)。 或者,我們可以在訓練過程中將每個神經元的輸出除以保持概率(這些替代方案并不完全等價,但它們工作得同樣好)。
要使用 Kera 實現 dropout,可以使用`keras.layers.Dropout`層。在訓練過程中,它隨機丟棄一些輸入(將它們設置為 0),并用保留概率來劃分剩余輸入。 訓練結束后,這個函數什么都不做,只是將輸入傳給下一層。下面的代碼將 dropout 正則化應用于每個緊密層之前,丟失率為 0.2:
```py
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dropout(rate=0.2),
keras.layers.Dense(300, activation="elu", kernel_initializer="he_normal"),
keras.layers.Dropout(rate=0.2),
keras.layers.Dense(100, activation="elu", kernel_initializer="he_normal"),
keras.layers.Dropout(rate=0.2),
keras.layers.Dense(10, activation="softmax")
])
```
> 警告:因為 dropout 只在訓練時有用,比較訓練損失和驗證損失會產生誤導。特別地,一個模型可能過擬合訓練集,但訓練和驗證損失相近。因此一定要不要帶 dropout 評估訓練損失(比如訓練后)。
如果觀察到模型過擬合,則可以增加 dropout 率(即,減少`keep_prob`超參數)。 相反,如果模型欠擬合訓練集,則應嘗試降低 dropout 率(即增加`keep_prob`)。 它也可以幫助增加大層的 dropout 率,并減少小層的 dropout 率。另外,許多優秀的架構只在最后一個隱藏層之后使用 dropout,如果全都加上 dropout 太強了,可以這么試試。
dropout 似乎減緩了收斂速度,但通常會在調參得當時使模型更好。 所以,這通常值得花費額外的時間和精力。
> 提示:如果想對一個自歸一化的基于 SELU 的網絡使用正則,應該使用 alpha dropout:這是一個 dropout 的變體,可以保留輸入的平均值和標準差(它是在 SELU 的論文中提出的,因為常規的 dropout 會破會自歸一化)。
### 蒙特卡洛(MC)dropout
Yarin Gal 和 Zoubin Ghahramani 在 2016 的一篇論文([https://arxiv.org/abs/1506.02142](https://links.jianshu.com/go?to=https%3A%2F%2Farxiv.org%2Fabs%2F1506.02142))中,追加了幾個使用 drop 的理由:
* 首先,這篇論文對 dropout 網絡(每個權重層前都有一個 Dropout 層)和貝葉斯推斷建立了理論聯系,從數學角度給予了證明。
* 第二,作者介紹了一種稱為 MC dropout 的方法,它可以提升任何訓練過的 dropout 模型的性能,并且無需重新訓練或修改,對模型存在的不確定性提供了一種更好的方法,也很容易實現。
如果這聽起來像一個廣告,看下面的代碼。它是 MC dropout 的完整實現,可以提升前面訓練的模型,并且沒有重新訓練:
```py
y_probas = np.stack([model(X_test_scaled, training=True)
for sample in range(100)])
y_proba = y_probas.mean(axis=0)
```
我們只是在訓練集上做了 100 次預測,設置`training=True`保證 Dropout 是活躍的,然后放到一起。因為 dropout 是開啟的,所有的預測都會不同。`predict()`返回一個矩陣,每行包含一個實例,每列是一個類。因為測試集有 10000 個實例和 10 個類,這個矩陣的形狀是[10000,10]。我們一共有 100 個這樣的矩陣,因此`y_proba`是一個形狀[100,10000,10]的數組。當對以一個維度維度(`axis=0`)做平均時,得到的是`y_proba`,形狀是[10000,10]的數組,就像和一次獨立預測的一樣。對開啟 dropout 的多次預測做平均,就得到了一個蒙特卡洛估計,會比單獨一次預測的可靠性更高。例如,看下模型對訓練集第一個實例的預測,關閉 dropout:
```py
>>> np.round(model.predict(X_test_scaled[:1]), 2)
array([[0\. , 0\. , 0\. , 0\. , 0\. , 0\. , 0\. , 0.01, 0\. , 0.99]],
dtype=float32)
```
這個模型大概率認定這張圖屬于類 9(靴子)。應該相信這個結果嗎?有無質疑空間呢?
再看看開啟 dropout 的預測:
```py
>>> np.round(y_probas[:, :1], 2)
array([[[0\. , 0\. , 0\. , 0\. , 0\. , 0.14, 0\. , 0.17, 0\. , 0.68]],
[[0\. , 0\. , 0\. , 0\. , 0\. , 0.16, 0\. , 0.2 , 0\. , 0.64]],
[[0\. , 0\. , 0\. , 0\. , 0\. , 0.02, 0\. , 0.01, 0\. , 0.97]],
[...]
```
當開啟 dropout,模型就沒那么確定了。雖然仍偏向類 9,但會在類 5(涼鞋)和類 7(運動鞋)猶豫。對第一維做平均,我們得到了下面的 MC dropout 預測:
```py
>>> np.round(y_proba[:1], 2)
array([[0\. , 0\. , 0\. , 0\. , 0\. , 0.22, 0\. , 0.16, 0\. , 0.62]],
dtype=float32)
```
模型仍認為這張圖屬于類 9,但置信度只有 62%,這比 99%可信讀了。知道可能屬于其它什么類,也有用。還可以再查看下概率估計的標準差:
```py
>>> y_std = y_probas.std(axis=0)
>>> np.round(y_std[:1], 2)
array([[0\. , 0\. , 0\. , 0\. , 0\. , 0.28, 0\. , 0.21, 0.02, 0.32]],
dtype=float32)
```
顯然,概率估計的方差很大:如果搭建的是一個對風險敏感的系統(比如醫療或金融),就要對這樣不確定的預測保持謹慎。另外,模型的準確率從 86.8 提升到了 86.9:
```py
>>> accuracy = np.sum(y_pred == y_test) / len(y_test)
>>> accuracy
0.8694
```
> 筆記:蒙特卡洛樣本的數量是一個可以調節的超參數。這個數越高,預測和不準確度的估計越高。但是,如果樣本數翻倍,推斷時間也要翻倍。另外,樣本數超過一定數量,提升就不大了。因此要取決于任務本身,在延遲和準確性上做取舍。
如果模型包含其它層行為特殊的層(比如批歸一化層),則不能像剛才那樣強行訓練模型。相反,你需要將`Dropout`層替換為`MCDropout`類:
```py
class MCDropout(keras.layers.Dropout):
def call(self, inputs):
return super().call(inputs, training=True)
```
這里,使用了`Dropout`的子類,并覆蓋了方法`call()`,使`training`參數變為`True`(見第 12 章)。相似的,可以通過`AlphaDropout`的子類定義一個`MCAlphaDropout`。如果是從零搭建模型,只需使用`MCDropout`而不是`Dropout`,你需要創建一個與老模型架構相同的新模型,替換`Dropout`層為`MCDropout`層,然后復制權重到新模型上。
總之,MC dropout 是一個可以提升 dropout 模型、提供更加不準確估計的神奇方法。當然,因為在訓練中仍然是常規 dropout,它仍然是一個正則器。
### 最大范數正則化
另一種在神經網絡中非常流行的正則化技術被稱為最大范數正則化:對于每個神經元,它約束輸入連接的權重`w`,使得 ∥ w ∥<sub>2</sub> ≤ r,其中`r`是最大范數超參數,∥ · ∥<sub>2</sub> 是 l2 范數。
最大范數正則沒有添加正則損失項到總損失函數中。相反,只是計算
我們通常通過在每個訓練步驟之后計算∥w∥<sub>2</sub>,并且如果需要的話可以如下剪切`W`。
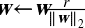
減少`r`增加了正則化的量,并有助于減少過擬合。 最大范數正則化還可以幫助減輕梯度消失/爆炸問題(如果不使用批歸一化)。
要在 Keras 中實現最大范數正則,需要設置每個隱藏層的`kernel_constraint`的`max_norm()`為一個合適的值,如下所示:
```py
keras.layers.Dense(100, activation="elu", kernel_initializer="he_normal",
kernel_constraint=keras.constraints.max_norm(1.))
```
每次訓練迭代之后,模型的`fit()`方法會調用`max_norm()`返回的對象,傳給它層的權重,并返回縮放過的權重,再代替層的權重。第 12 章會看到,如果需要的話可以定義自己的約束函數。你還可以通過設置參數`bias_constraint`約束偏置項。
`max_norm()`函數有一個參數`axis`,默認為 0。緊密層權重的形狀通常是[輸入數,神經元數],因此設置`axis=0`,意味最大范數約束會獨立作用在每個神經元的權重矢量上。如果你想對卷積層使用最大范數,一定要合理設置`axis`(通常`axis=[0,1,2]`)。
## 總結和實踐原則
本章介紹了許多方法,讀者可能納悶到底該用哪個呢。用哪種方法要取決于任務,并沒有統一的結論,表 11-3 的總結可用于大多數情況,不需要調節太多超參數。但是,也不要死守這些默認值!
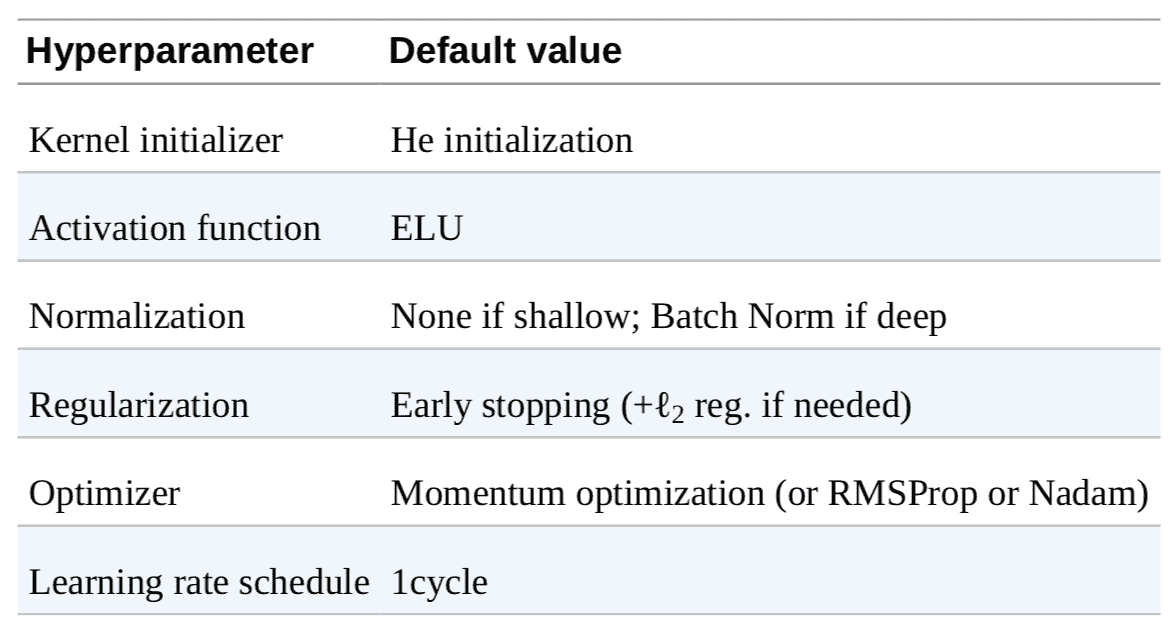表 11-3 默認 DNN 配置
如果網絡只有緊密層,則可以是自歸一化的,可以使用表 11-4 的配置。
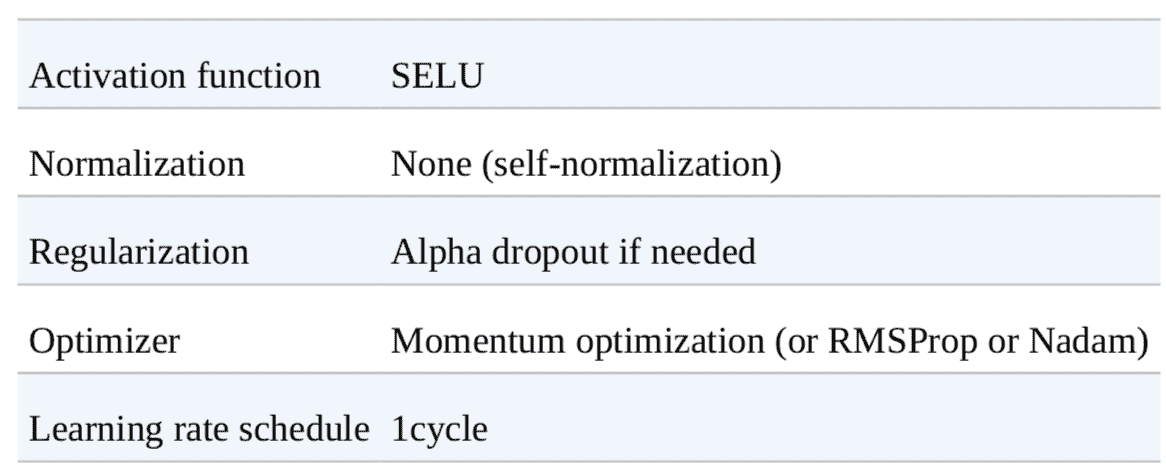表 11-4 自歸一化網絡的 DNN 配置
不要忘了歸一化輸入特征!還應該嘗試復用部分預訓練模型,如果它處理的是一個想死任務,或者如果有許多無便數據時使用無監督預訓練,或者有許多相似任務的標簽數據時使用輔助任務的語序年。
雖然這些指導可以應對大部分情況,但有些例外:
* 如果需要系數模型,你可以使用?1 正則(可以在訓練后,將部分小權重設為零)。如果需要一個再稀疏點的模型,可以使用 TensorFlow Model Optimization Toolkit,它會破壞自歸一化,所以要使用默認配置。
* 如果需要一個地延遲模型(預測快),層要盡量少,對前一層使用批歸一化,使用更快的激活函數,比如 leaky ReLU 或 ReLU。稀疏模型也快。最后,將浮點精度從 32 位降到 16 位,甚至 8 位。還有,嘗試 TF-MOT。
* 如果搭建的是風險敏感的模型,或者推斷延遲不是非常重要,可以使用 MC dropout 提升性能,得到更可靠的概率估計和不確定估計。
有了這些原則,就可以開始訓練非常深的網絡了。希望你現在對 Keras 有足夠的自信。隨著深入,可能需要寫自定義的損失函數或調解訓練算法。對于這樣的情況,需要使用 TensorFlow 的低級 API,見下一章。
## 練習
1. 使用 He 初始化隨機選擇權重,是否可以將所有權重初始化為相同的值?
2. 可以將偏置初始化為 0 嗎?
3. 說出 SELU 激活功能與 ReLU 相比的三個優點。
4. 在哪些情況下,您想要使用以下每個激活函數:SELU,leaky ReLU(及其變體),ReLU,tanh,logistic 以及 softmax?
5. 如果將`momentum`超參數設置得太接近 1(例如,0.99999),會發生什么情況?
6. 請列舉您可以生成稀疏模型的三種方法。
7. dropout 是否會減慢訓練? 它是否會減慢推斷(即預測新的實例)?MC dropout 呢?
8. 在 CIFAR10 圖片數據集上訓練一個深度神經網絡:
1. 建立一個 DNN,有 20 個隱藏層,每層 100 個神經元,使用 He 初始化和 ELU 激活函數。
2. 使用 Nadam 優化和早停,嘗試在 CIFAR10 上進行訓練,可以使用`keras.datasets.cifar10.load_?data()`加載數據。數據集包括 60000 張 32x32 的圖片(50000 張訓練,10000 張測試)有 10 個類,所以需要 10 個神經元的 softmax 輸出層。記得每次調整架構或超參數之后,尋找合適的學習率。
3. 現在嘗試添加批歸一化并比較學習曲線:它是否比以前收斂得更快? 它是否會產生更好的模型?對訓練速度有何影響?
4. 嘗試用 SELU 替換批歸一化,做一些調整,確保網絡是自歸一化的(即,標準化輸入特征,使用 LeCun 正態初始化,確保 DNN 只含有緊密層)。
5. 使用 alpha dropout 正則化模型。然后,不訓練模型,使用 MC Dropout 能否提高準確率。
6. 用 1 循環調度重新訓練模型,是否能提高訓練速度和準確率。
參考答案見附錄 A。
