[TOC]
## 1.概念
**分類**(classification)是通過對具有類別的對象的數據集進行學習,概括其主要特征,構建分類模型,根據該模型預測對象的類別的一種數據挖掘和機器學習技術。
## 2.模型的誤差
* 誤差(error):模型的實際預測輸出與樣本的真實輸出之間的差異
* 訓練誤差(training error)或經驗誤差( empirical error):模型在訓練集上的誤差
* 泛化誤差( generalization error):在新樣本上的誤差
## 3.分類的評估
* **混淆矩陣**

* **準確率**(Accuracy): 衡量所有樣本被分類準確的比例
Accuracy=(TP+TN)/(TP+FP+TN+FN)
* **精確率**(Precision): 也叫查準率,衡量正樣本的分類準確率,就是說被預測為正樣本的樣本有多少是真的正樣本。
Precision=TP/(TP+FP)
* **召回率**(Recall):表示有多少正樣本被準確識別
Recall=TP/(TP+FN)
* **F1-score**:精確率和召回率的調和平均
2/F\_1 =1/P+1/R?F\_1 = 2PR/(P+R) = 2TP/(2TP+FP+FN)
* **roc曲線**(Receiver Operating Characteristic,接受者操作特征曲線),指在特定刺激條件下,以被試者在不同判斷標準下所得的誤報率FPR為橫坐標,以擊中率TPR為縱坐標,畫得的各點的連線,是一種評價分類模型的可視化工具.
1. 橫坐標是FPR(False Positive Rate)或稱誤報率: FPR = FP/(TN+FP)
2. 縱坐標是TPR(True Positive Rate)或稱召回率: TPR = TP/(TP+FN)
* **AUC**(Area Under Curve)表示ROC曲線下方的面積,可以對模型的好壞進行量化
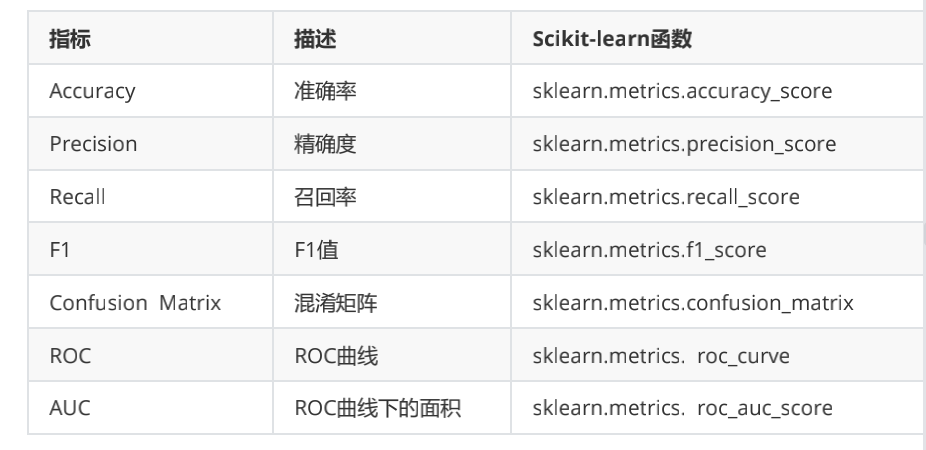
## 4.數據集的劃分

* 訓練數據集(train dataset):用來學習的樣本集,用于模型參數的擬合。
* 驗證數據集(validation dataset):用來調整模型超參數的樣本集,如在神經網絡中選擇隱藏層神經元的數量。
* 測試數據集(test dataset):用于對已經訓練好的模型進行性能評估的樣本集,用來評估最終模型的泛化能力。但不能作為調參、選擇特征等算法相關的選擇的依據。
### **1)劃分**
* model\_selection.train\_test\_split
### **2)K折交叉驗證:**
* cross\_val\_score
### **5.過擬合問題**
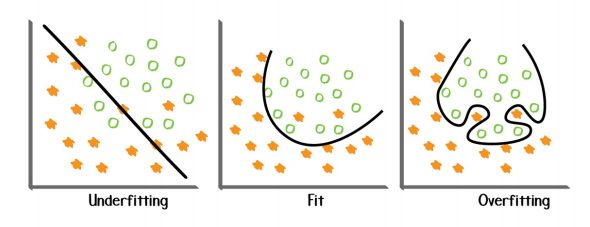
* 過擬合:做的太過好以至于偏離了原本,泛化能力差
1. 可能的原因:
* 使用的模型比較復雜,學習能力過強
* 有噪聲存在
* 數據量有限
2. 過擬合解決方式:
* 交叉驗證
* 及時終止(當驗證集上的效果變差的時候)
* 找到更多的數據
* 尋找最優參數
* 增大正則化系數:正則化是指人為地迫使模型變得更簡單的一系列技術
* 刪除無用特征
* 集成學習
* 欠擬合:泛化能力強,但過于泛化
1. 可能的原因:使用的模型過于簡單
2. 解決辦法:
* 找到更多的特征
* 減少正則化系數
* 從一個非常簡單的模型開始,以此作為基準
**Sklearn中提供的相應方法:**
* 網絡搜索:model_selection. GridSearchCV
* 尋找訓練集大小:學習曲線model_selection. learning_curve
* 尋找參數的最優:驗證曲線model_selection. validation_curve
### **6. KNN**
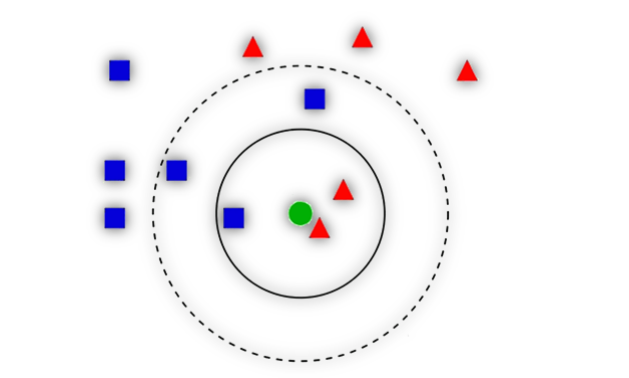
距離的度量
**1).算法描述**
**2)優缺點**
**3)變種**
* 加權KNN:增加鄰居的權重,比如距離越近權重越高。
* RadiusNeighbors:使用一定半徑內的點取代距離最近的k個點
**4) sklearn提供的方法**
* neighbors. KNeighborsClassifier
* neighbors. RadiusNeighborsClassifier
### 7.決策樹
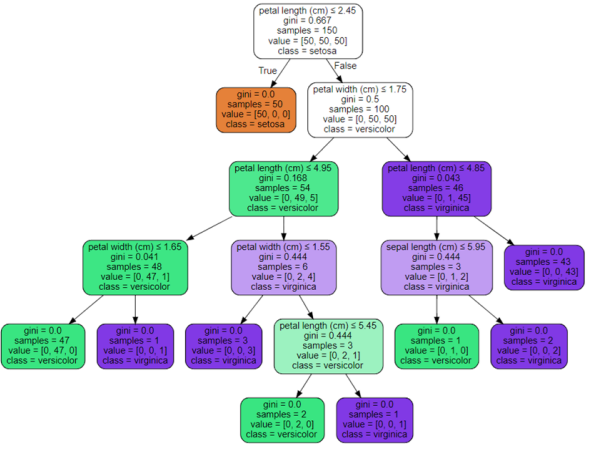
**1)核心:**
* 選哪個特征進行分裂以及如何分裂
* 如何讓樹停止生長
**2)算法:**
* ID3 <==>信息增益:事件中某一影響因素的不確定性度量對事件信息不確定性減少的程度,即得知特征X的信息而使得類Y的信息不確定性減少的程度。
* C4.5 <==>信息增益率
* CART <==>基尼指數
**3)sklearn中的方法:**
* tree.DecisionTreeClassifier
### 8.樸素貝葉斯
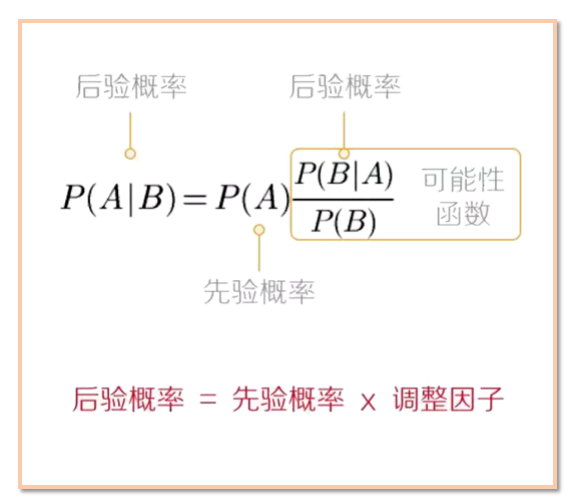
樸素貝葉斯算法(Naive Bayes)是基于貝葉斯定理與特征條件獨立假設的分類方法。
**1)樸素貝葉斯的工作過程**
(1)設D是訓練元組和它們相關聯的類標號的集合。通常,每個元組用一個n維屬性向量X={x_1,x_2,…,x_n}表示,描述由n個屬性對元組的n個測量。
(2)假定有m個類y\_1,y\_2,..., y\_m。給定元組X,分類法將預測X屬于具有最高后驗概率的類(在條件X下)。P(y\_i |X) = (P(X|y\_i)P(y\_i))/(P(X))由于P(X)對所有類為常數,所以只需要P(X│y\_i )P(y\_i )最大即可。
(3)給定具有許多屬性的數據 集,計算P(X│y\_i )的開銷可能非常大。為了降低P(X│y\_i )的開銷,可以做**類條件獨立**的樸素假定。給定元組的類標號,假定屬性值條件地相互獨立(即屬性之間不存在依賴關系)。因此
P(X│y\_i ) =∏\_(k=1)^n?〖P(〗x\_k |y\_i) = P(x\_1 |y\_i) P(x\_2 |y\_i)???P(x\_n |y\_i)
(4)該分類算法預測輸入元組X的類為y\_i,當且僅當P(X|y\_i)P(y\_i) > P(X|y\_j)P(y\_j) 1≤j≤m, j≠i
**2)優缺點**
**3)分類**
* 多項式模型: naive_bayes.MultinomialNB
* 補集樸素貝葉斯: naive_bayes.ComplementNB (是標準多項式樸素貝葉斯算法的改進。該算法能夠解決樣本不平衡問題,并且能夠一定程度上忽略樸素假設的補集樸素貝葉斯。)
* 高斯模型: naive_bayes.GaussianNB
* 伯努利模型: naive_bayes.BernoulliNB
### 9.支持向量機
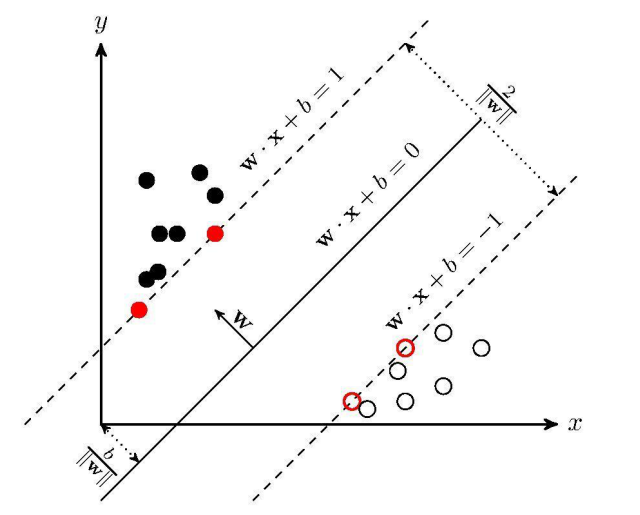
支持向量機(support vector machines)是一種二分類模型,它的目的是尋找一個超平面來對樣本進行分割,分割的原則是間隔最大化,最終轉化為一個凸二次規劃問題來求解:
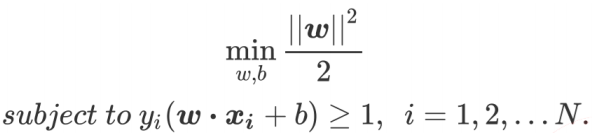
**1)三種情況**
* 線性可分
* 近似線性可分:引入松弛變量
* 線性不可分:引入核函數
**2)svm.SVC**
