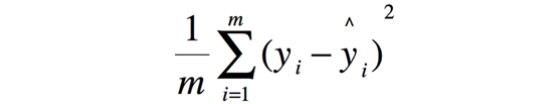
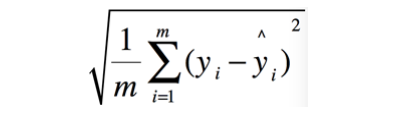
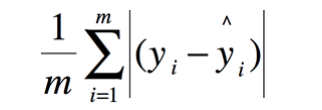
[TOC] ## 1.概念 * 回歸分析(Regression Analysis)是確定兩種或兩種以上變量間相互依賴的定量關系的一種統計分析方法。 * 回歸與分類的區別：回歸預測的是連續變量（數值），分類預測的是離散變量（類別）。 2.回歸的評估 * 均方誤差（Mean Squared Error, MSE）  注意：在使用cross\_val\_score計算時，MSE的分數用“neg\_mean\_squared\_error”計算一個負值，類為score代表的是分數，越高越好，顯然MSE是越低越好，它是一種loss，越低越好。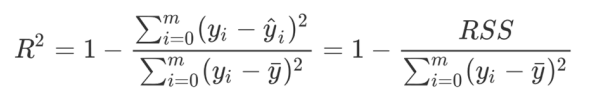 * 均方根誤差（Root Mean Squared Error, MSE）  * 平均絕對誤差（Mean Absolute Error, MAE）  * 中值絕對誤差（Median Absolute Error） * 決定系數（Coefficient of Determination，R2）  * sklearn的metrics模塊中提供了如下回歸的相關指標： ? max_error ?mean_absolute_error ?mean_squared_error ?mean_squared_log_error ?median_absolute_error ?mean_tweedie_deviance ?mean_poisson_deviance ?mean_gamma_deviance ?r2_score ?explained_variance_score **3）線性回歸** 線性回歸(Linear Regression)：因變量（Y）和一個或多個自變量（X）之間建立一種線性方程關系 * linear_model.LinearRegression * 重要屬性：coef_和intercept_ * 求解方法：最小二乘法 * 問題—多重線性關系： * “精確相關關系”（完全相關）：行列式為0 * “高度相關關系”：行列式不為0，但是一個非常接近0的數 **4）Ridge（嶺回歸）** 嶺回歸,又稱為吉洪諾夫正則化（Tikhonov regularization）,在多元線性回歸的損失函數上加上了正則項，表達為系數ω的L2范式（即系數ω的平方項）乘以正則化系數。 * linear_model.Ridge **5）Lasso回歸** Lasso回歸，Lasso全稱最小絕對收縮和選擇算子（least absolute shrinkage and selection operator），使用的是系數ω的L1范式（L1范式則是系數ω的絕對值）乘以正則化系數 。 * linear_model.Lasso **6）彈性網(Elastic Net)** 彈性網(Elastic Net)，是一種使用L1,L2范式作為先驗正則項訓練的線性回歸模型。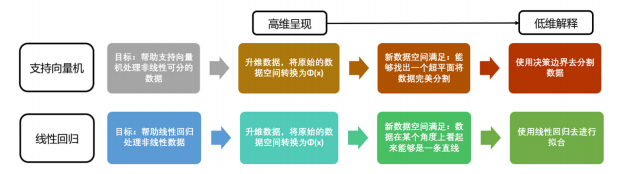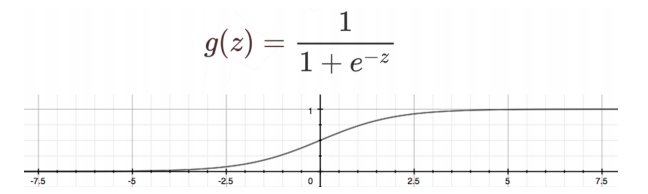 **7）多項式回歸**  對線性回歸問題，如果數據不是線性關系，采用**多項式變換**的方式對特征數據進行升維 * preprocessing.PolynomialFeatures **8)邏輯回歸**  * linear_model.LogisticRegression