通過前面課時的學習，相信你已經掌握了線性表的基本原理，以及如何完成線性表結構下的增刪查操作。 線性表是使用非常廣泛的一類數據結構，它對數據的順序非常敏感，而且它對數據的增刪操作非常靈活。在有序排列的數據中，可以靈活的執行增刪操作，就好像是為排好隊的數據增加了插隊的入口。這既是靈活性也是缺陷，原因在于它的靈活性在某種程度上破壞了數據的原始順序。在某些需要嚴格遵守數據處理順序的場景下，我們就需要對線性表予以限制了。經過限制后的線性表，它們通常會被賦予一些新的名字。這一課時，我們就來學習其中一個限制后的線性表--棧。 #### 棧是什么 你需要牢記一點，棧是一種特殊的線性表。棧與線性表的不同，體現在增和刪的操作。具體而言，棧的數據結點必須后進先出。后進的意思是，棧的數據新增操作只能在末端進行，不允許在棧的中間某個結點后新增數據。先出的意思是，棧的數據刪除操作也只能在末端進行，不允許在棧的中間某個結點后刪除數據。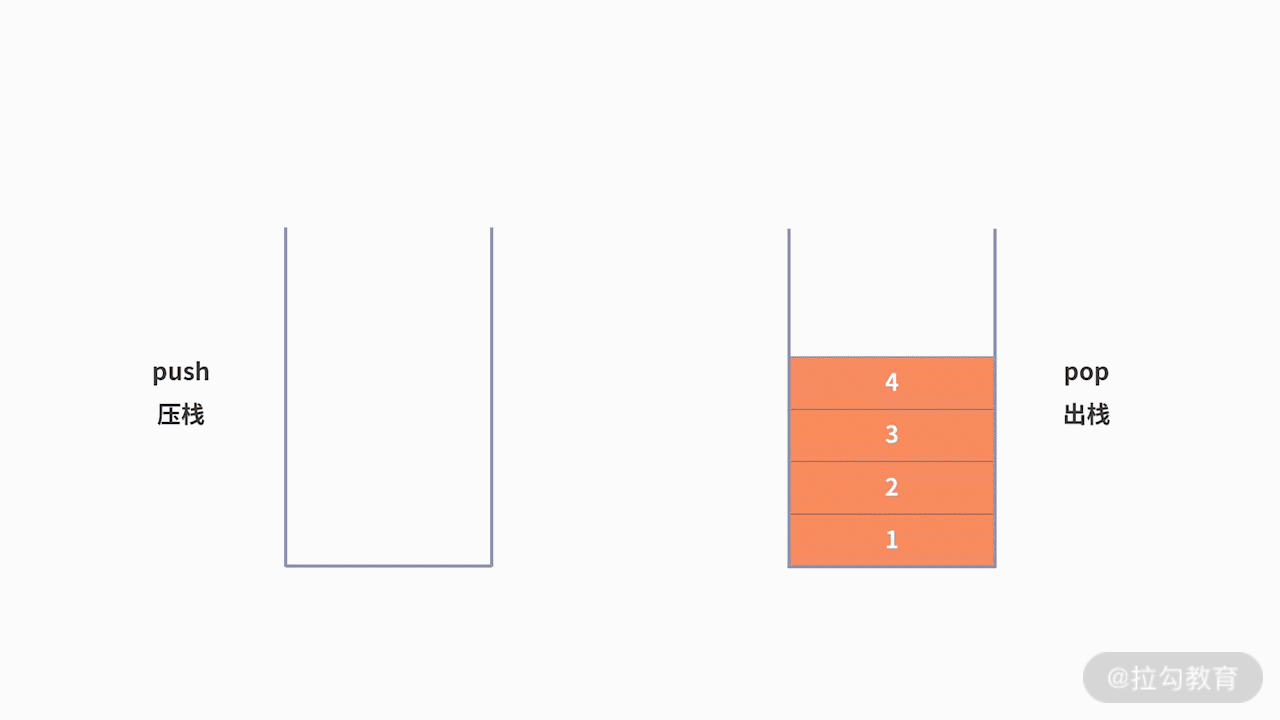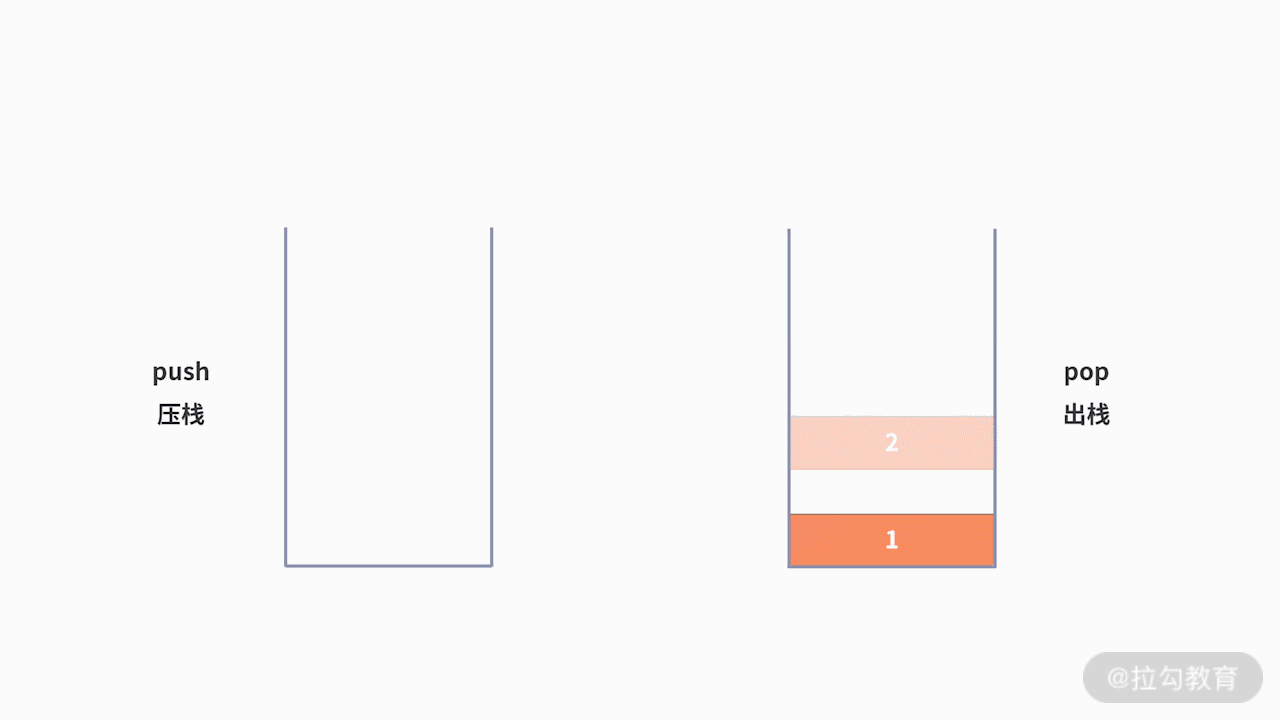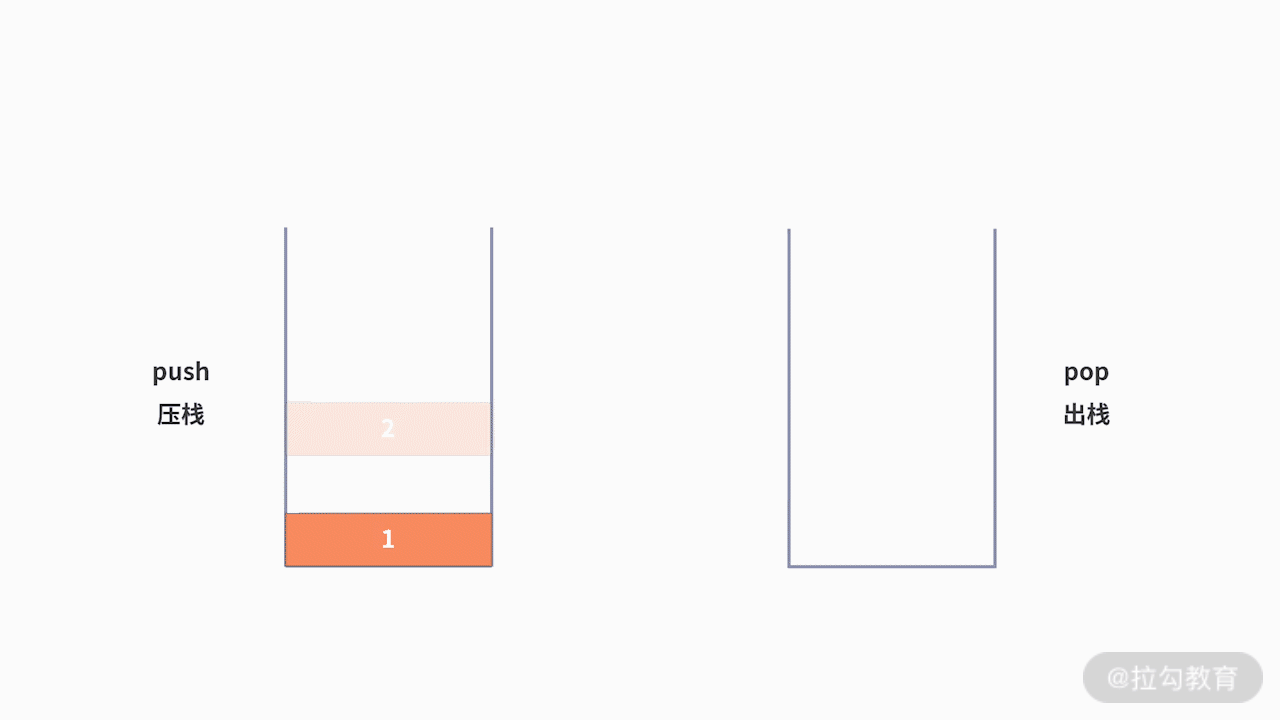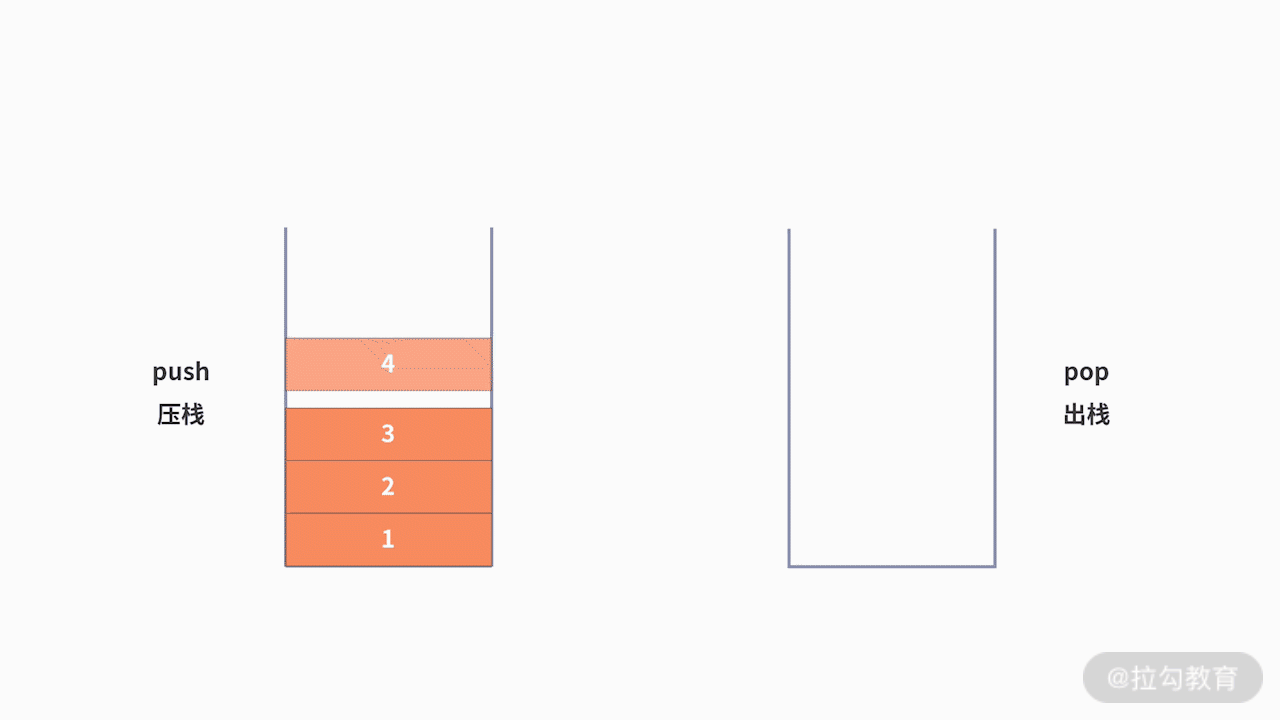 也就是說，棧的數據新增和刪除操作只能在這個線性表的表尾進行，即在線性表的基礎上加了限制。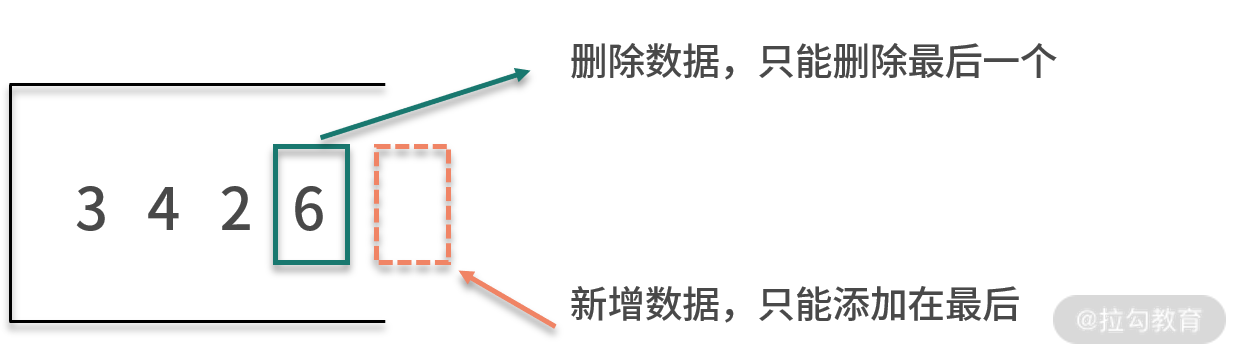如下圖所示：  因此，棧是一種后進先出的線性表。棧對于數據的處理，就像用磚頭蓋房子的過程。對于蓋房子而言，新的磚頭只能放在前一個磚頭上面；而對于拆房子而言，我們需要從上往下拆磚頭。  宏觀上來看，與數組或鏈表相比，棧的操作更為受限，那為什么我們要用這種受限的棧呢？其實，單純從功能上講，數組或者鏈表可以替代棧。然而問題是，數組或者鏈表的操作過于靈活，這意味著，它們過多暴露了可操作的接口。這些沒有意義的接口過多，當數據量很大的時候就會出現一些隱藏的風險。一旦發生代碼 bug 或者受到攻擊，就會給系統帶來不可預知的風險。雖然棧限定降低了操作的靈活性，但這也使得棧在處理只涉及一端新增和刪除數據的問題時效率更高。 舉個實際的例子，瀏覽器都有頁面前進和后退功能，這就是個很典型的后進先出的場景。假設你先后訪問了五個頁面，分別標記為 1、2、3、4、5。當前你在頁面 5，如果執行兩次后退，則退回到了頁面 3，如果再執行一次前進，則到了頁面 4。處理這里的頁面鏈接存儲問題，棧就應該是我們首選的數據結構。  棧既然是線性表，那么它也包含了表頭和表尾。不過在棧結構中，由于其操作的特殊性，會對表頭和表尾的名字進行改造。表尾用來輸入數據，通常也叫作棧頂（top）；相應地，表頭就是棧底（bottom）。棧頂和棧底是用來表示這個棧的兩個指針。跟線性表一樣，棧也有順序表示和鏈式表示，分別稱作順序棧和鏈棧。 #### 棧的基本操作 如何通過棧這個后進先出的線性表，來實現增刪查呢？初始時，棧內沒有數據，即空棧。此時棧頂就是棧底。當存入數據時，最先放入的數據會進入棧底。接著加入的數據都會放入到棧頂的位置。如果要刪除數據，也只能通過訪問棧頂的數據并刪除。對于棧的新增操作，通常也叫作 push 或壓棧。對于棧的刪除操作，通常也叫作 pop 或出棧。對于壓棧和出棧，我們分別基于順序棧和鏈棧進行討論。  * [ ] 順序棧 棧的順序存儲可以借助數組來實現。一般來說，會把數組的首元素存在棧底，最后一個元素放在棧頂。然后定義一個 top 指針來指示棧頂元素在數組中的位置。假設棧中只有一個數據元素，則 top = 0。一般以 top 是否為 -1 來判定是否為空棧。當定義了棧的最大容量為 StackSize 時，則棧頂 top 必須小于 StackSize。 當需要新增數據元素，即入棧操作時，就需要將新插入元素放在棧頂，并將棧頂指針增加 1。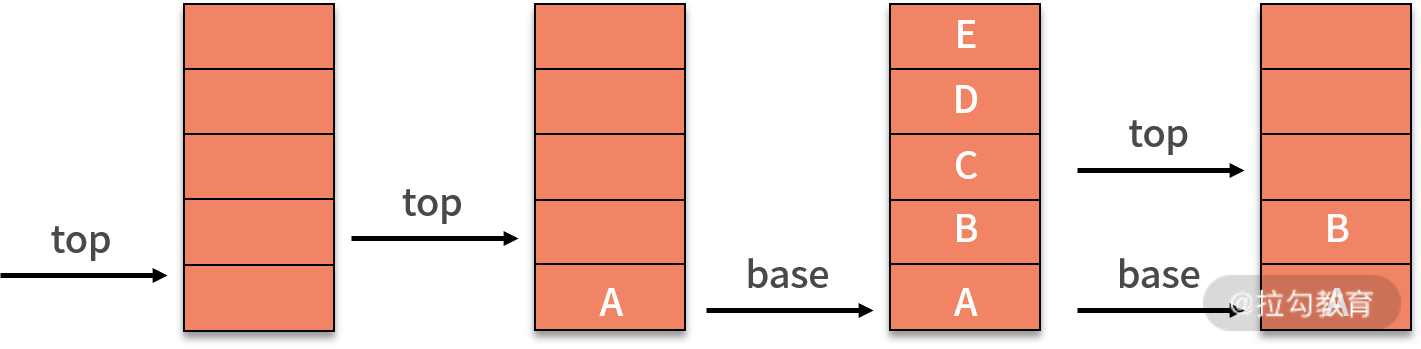如下圖所示：  刪除數據元素，即出棧操作，只需要 top - 1 就可以了。 對于查找操作，棧沒有額外的改變，跟線性表一樣，它也需要遍歷整個棧來完成基于某些條件的數值查找。 * [ ] 鏈棧 關于鏈式棧，就是用鏈表的方式對棧的表示。通常，可以把棧頂放在單鏈表的頭部，如下圖所示。由于鏈棧的后進先出，原來的頭指針就顯得毫無作用了。因此，對于鏈棧來說，是不需要頭指針的。相反，它需要增加指向棧頂的 top 指針，這是壓棧和出棧操作的重要支持。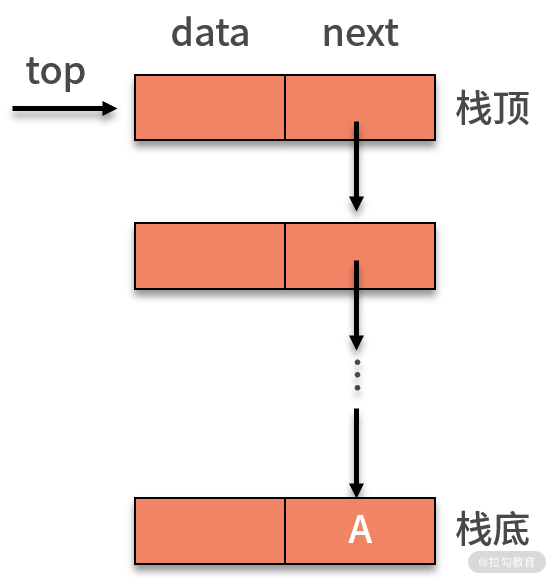  對于鏈棧，新增數據的壓棧操作，與鏈表最后插入的新數據基本相同。需要額外處理的，就是棧的 top 指針。如下圖所示，插入新的數據，則需要讓新的結點指向原棧頂，即 top 指針指向的對象，再讓 top 指針指向新的結點。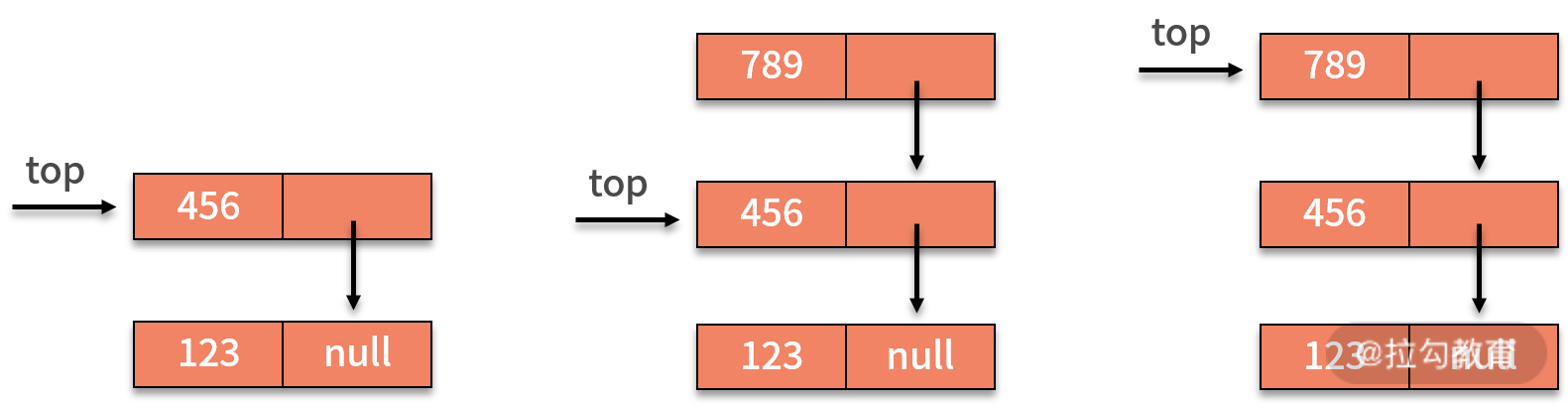  在鏈式棧中進行刪除操作時，只能在棧頂進行操作。因此，將棧頂的 top 指針指向棧頂元素的 next 指針即可完成刪除。對于鏈式棧來說，新增刪除數據元素沒有任何循環操作，其時間復雜度均為 O(1)。 對于查找操作，相對鏈表而言，鏈棧沒有額外的改變，它也需要遍歷整個棧來完成基于某些條件的數值查找。 通過分析你會發現，不管是順序棧還是鏈棧，數據的新增、刪除、查找與線性表的操作原理極為相似，時間復雜度完全一樣，都依賴當前位置的指針來進行數據對象的操作。區別僅僅在于新增和刪除的對象，只能是棧頂的數據結點。 #### 棧的案例 接下來，我們一起來看兩個棧的經典案例，從中你可以更深切地體會到棧所發揮出的價值。 例 1，給定一個只包括 '('，')'，'{'，'}'，'['，']' 的字符串，判斷字符串是否有效。有效字符串需滿足：左括號必須與相同類型的右括號匹配，左括號必須以正確的順序匹配。例如，{ [ ( ) ( ) ] } 是合法的，而 { ( [ ) ] } 是非法的。 這個問題很顯然是棧發揮價值的地方。原因是，在匹配括號是否合法時，左括號是從左到右依次出現，而右括號則需要按照“后進先出”的順序依次與左括號匹配。因此，實現方案就是通過棧的進出來完成。 具體為，從左到右順序遍歷字符串。當出現左括號時，壓棧。當出現右括號時，出棧。并且判斷當前右括號，和被出棧的左括號是否是互相匹配的一對。如果不是，則字符串非法。當遍歷完成之后，如果棧為空。則合法。如下圖所示：  代碼如下： ``` public static void main(String[] args) { String s = "{[()()]}"; System.out.println(isLegal(s)); } private static int isLeft(char c) { if (c == '{' || c == '(' || c == '[') { return 1; } else { return 2; } } private static int isPair(char p, char curr) { if ((p == '{' && curr == '}') || (p == '[' && curr == ']') || (p == '(' && curr == ')')) { return 1; } else { return 0; } } private static String isLegal(String s) { Stack stack = new Stack(); for (int i = 0; i < s.length(); i++) { char curr = s.charAt(i); if (isLeft(curr) == 1) { stack.push(curr); } else { if (stack.empty()) { return "非法"; } char p = (char) stack.pop(); if (isPair(p, curr) == 0) { return "非法"; } } } if (stack.empty()) { return "合法"; } else { return "非法"; } } ``` 例 2，瀏覽器的頁面訪問都包含了后退和前進功能，利用棧如何實現？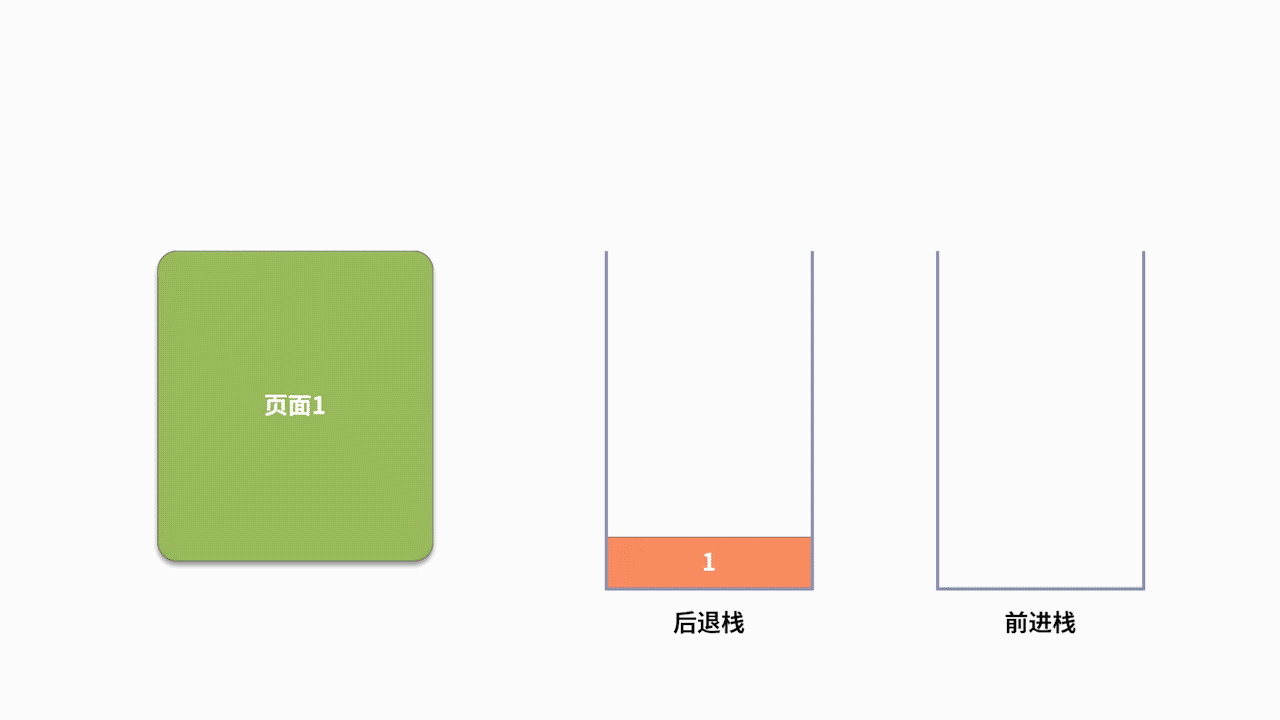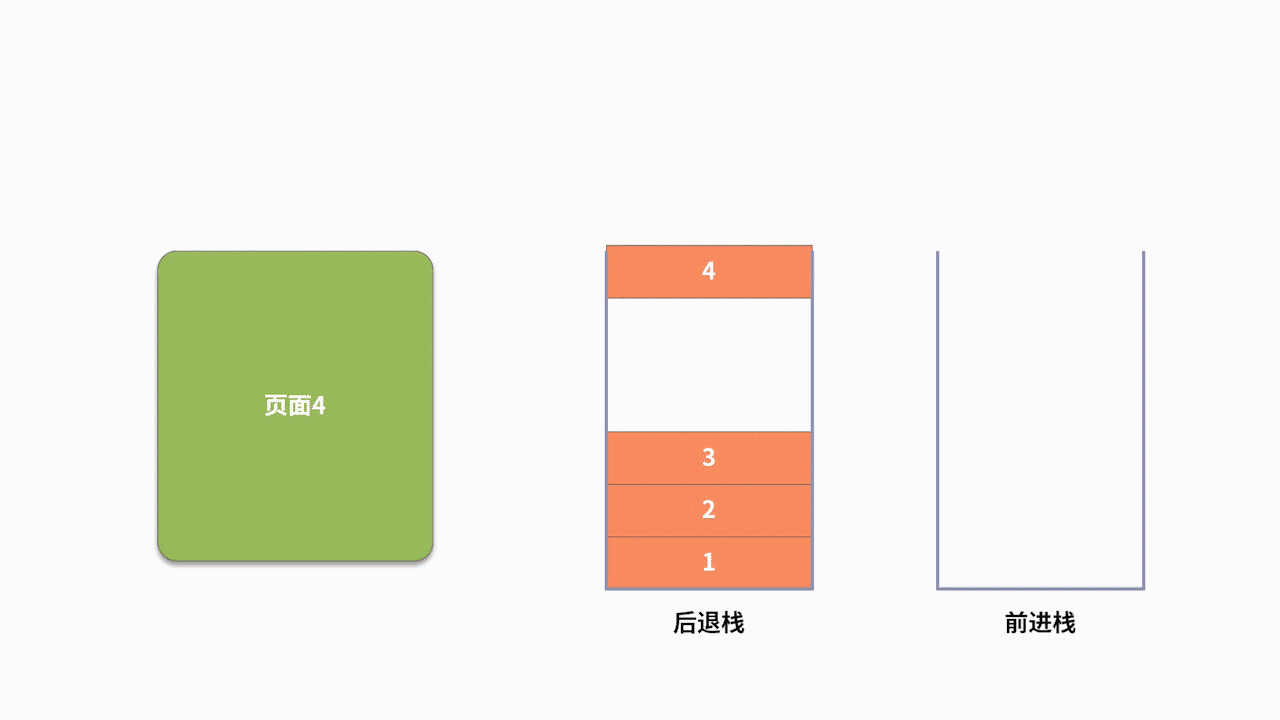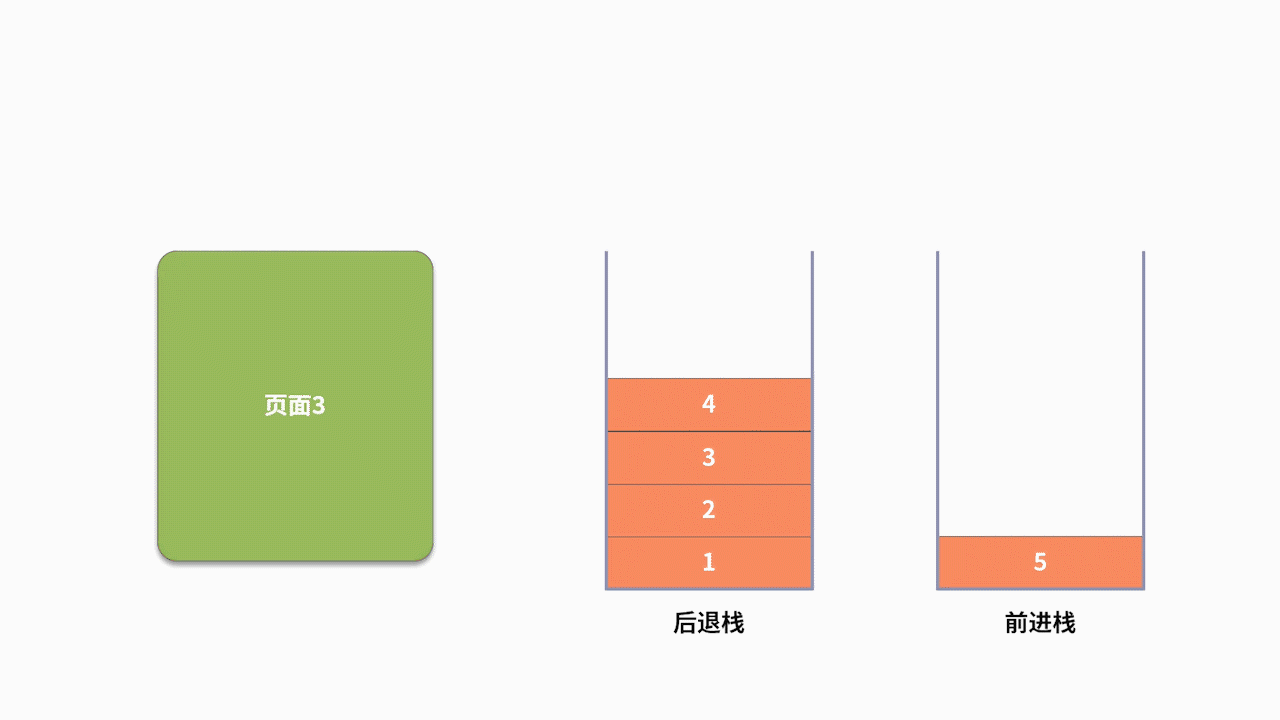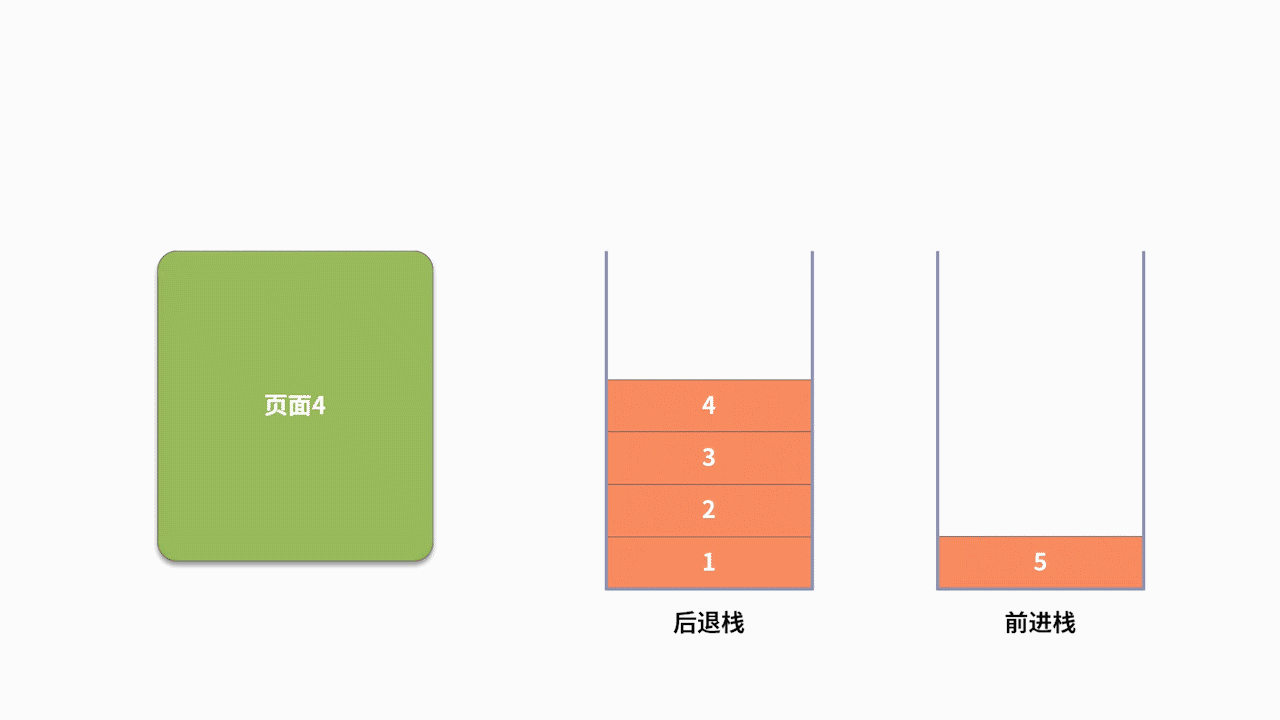 我們利用瀏覽器上網時，都會高頻使用后退和前進的功能。比如，你按照順序先后訪問了 5 個頁面，分別標記為 1、2、3、4、5。現在你不確定網頁 5 是不是你要看的網頁，需要回退到網頁 3，則需要使用到兩次后退的功能。假設回退后，你發現網頁 4 有你需要的信息，那么就還需要再執行一次前進的操作。 為了支持前進、后退的功能，利用棧來記錄用戶歷史訪問網頁的順序信息是一個不錯的選擇。此時需要維護兩個棧，分別用來支持后退和前進。當用戶訪問了一個新的頁面，則對后退棧進行壓棧操作。當用戶后退了一個頁面，則后退棧進行出棧，同時前進棧執行壓棧。當用戶前進了一個頁面，則前進棧出棧，同時后退棧壓棧。我們以用戶按照 1、2、3、4、5、4、3、4 的瀏覽順序為例，兩個棧的數據存儲過程，如下圖所示：  #### 總結 好的，這節課的內容就到這里了。這一節的內容主要圍繞棧的原理、棧對于數據的增刪查操作展開。 棧繼承了線性表的優點與不足，是個限制版的線性表。限制的功能是，只允許數據從棧頂進出，這也就是棧后進先出的性質。不管是順序棧還是鏈式棧，它們對于數據的新增操作和刪除操作的時間復雜度都是 O(1）。而在查找操作中，棧和線性表一樣只能通過全局遍歷的方式進行，也就是需要 O(n) 的時間復雜度。 棧具有后進先出的特性，當你面對的問題需要高頻使用新增、刪除操作，且新增和刪除操作的數據執行順序具備后來居上的相反關系時，棧就是個不錯的選擇。例如，瀏覽器的前進和后退，括號匹配等問題。棧在代碼的編寫中有著很廣泛的應用，例如，大多數程序運行環境都有的子程序的調用，函數的遞歸調用等。這些問題都具有后進先出的特性。關于遞歸，我們會在后續的課程單獨進行分析。 #### 練習題 下面我們給出本課時的練習題。在上一課時中，我們的習題是，給定一個包含 n 個元素的鏈表，現在要求每 k 個節點一組進行翻轉，打印翻轉后的鏈表結果。其中，k 是一個正整數，且 n 可被 k 整除。 例如，鏈表為 1 -> 2 -> 3 -> 4 -> 5 -> 6，k = 3，則打印 321654。仍然是這道題，我們試試用棧來解決它吧。