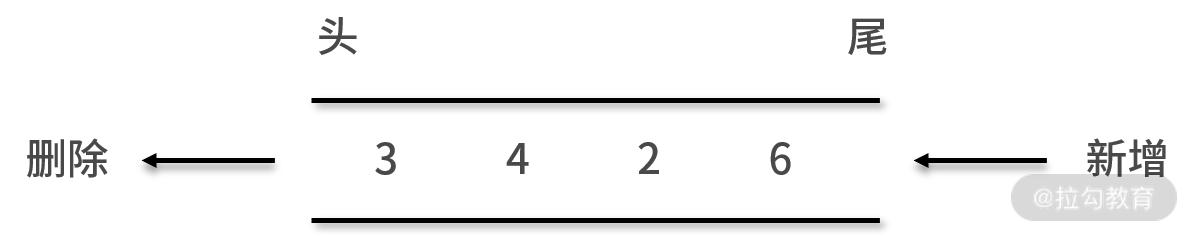
通過前面課時的學習，你學會了數據結構中可以靈活增刪數據的線性表。在需要嚴格遵守數據處理順序的場景下，我們對線性表予以限制，那么就得到了后進先出的數據結構，棧。與之對應的還有一種限制的線性表，它遵循先進先出的性質，這就是隊列。這一課時我們就來學習隊列的增刪查。 #### 隊列是什么 與棧相似，隊列也是一種特殊的線性表，與線性表的不同之處也是體現在對數據的增和刪的操作上。 隊列的特點是先進先出： * 先進，表示隊列的數據新增操作只能在末端進行，不允許在隊列的中間某個結點后新增數據; * 先出，隊列的數據刪除操作只能在始端進行，不允許在隊列的中間某個結點后刪除數據。也就是說隊列的增和刪的操作只能分別在這個隊列的隊尾和隊頭進行，如下圖所示：  與線性表、棧一樣，隊列也存在這兩種存儲方式，即順序隊列和鏈式隊列： * 順序隊列，依賴數組來實現，其中的數據在內存中也是順序存儲。 * 而鏈式隊列，則依賴鏈表來實現，其中的數據依賴每個結點的指針互聯，在內存中并不是順序存儲。鏈式隊列，實際上就是只能尾進頭出的線性表的單鏈表。 如下圖所示，我們將隊頭指針指向鏈隊列的頭結點，隊尾指針指向終端結點。不管是哪種實現方式，一個隊列都依賴隊頭（front）和隊尾（rear）兩個指針進行唯一確定。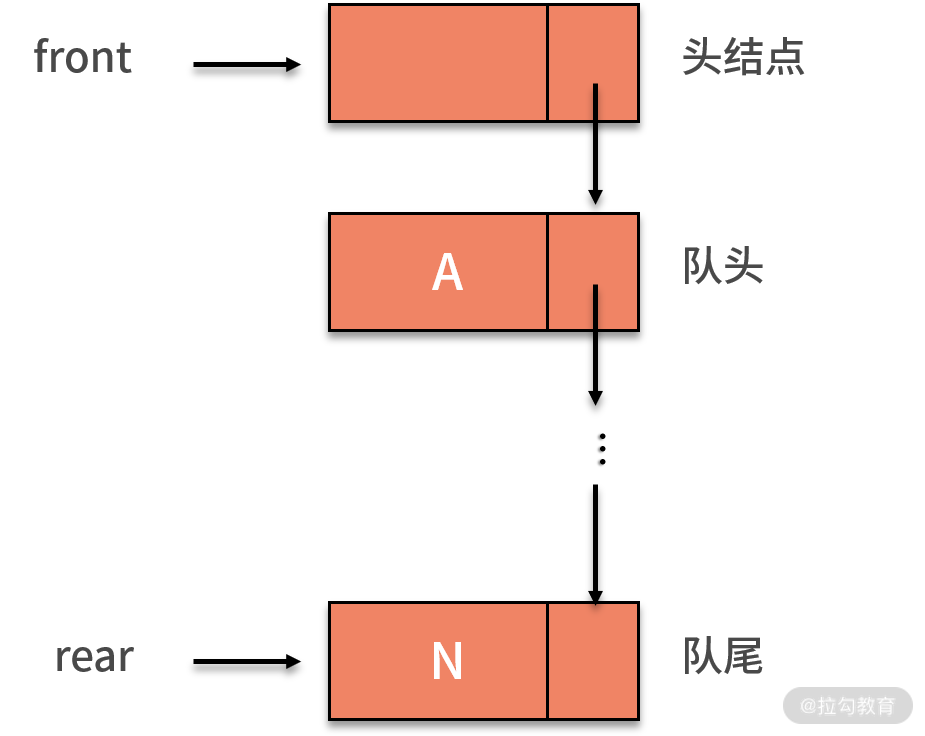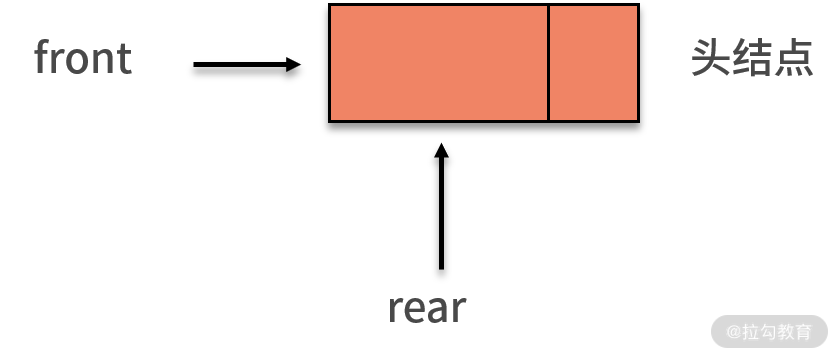  當隊列為空時，front 和 rear 都指向頭結點，如下圖所示：  #### 隊列對于數據的增刪查處理 隊列從隊頭（front）刪除元素，從隊尾（rear）插入元素。對于一個順序隊列的數組來說，會設置一個 front 指針來指向隊頭，并設置另一個 rear 指針指向隊尾。當我們不斷進行插入刪除操作時，頭尾兩個指針都會不斷向后移動。 為了實現一個有 k 個元素的順序存儲的隊列，我們需要建立一個長度比 k 大的數組，以便把所有的隊列元素存儲在數組中。隊列新增數據的操作，就是利用 rear 指針在隊尾新增一個數據元素。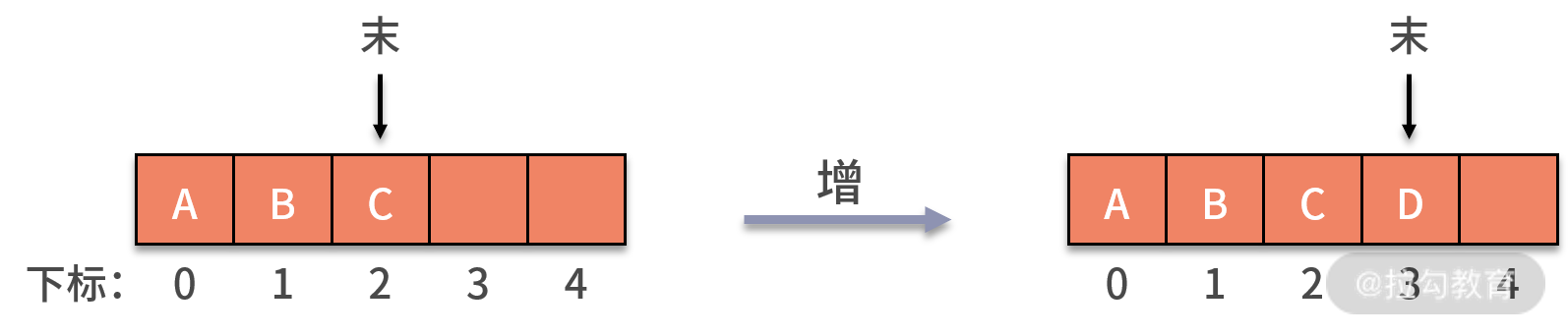這個過程不會影響其他數據，時間復雜度為 O(1)，狀態如下圖所示：  隊列刪除數據的操作與棧不同。隊列元素出口在隊列頭部，即下標為 0 的位置。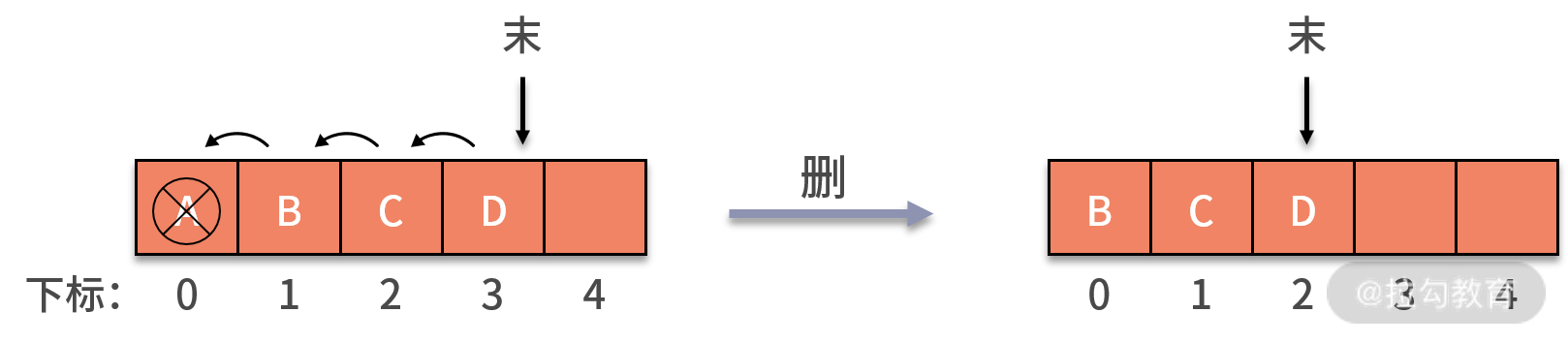當利用 front 指針刪除一個數據時，隊列中剩余的元素都需要向前移動一個位置，以保證隊列頭部下標為 0 的位置不為空，此時時間復雜度就變成 O(n) 了，狀態如下圖所示：  我們看到，front 指針刪除數據的操作引發了時間復雜度過高的問題，那么我們該如何解決呢？我們可以通過移動指針的方式來刪除數據，這樣就不需要移動剩余的數據了。但是，這樣的操作，也可能會產生數組越界的問題。接下來，我們來詳細討論一下。 我們一起來看一個利用順序隊列，持續新增數據和刪除數據的例子。 初始時，定義了長度為 5 的數組，front 指針和 rear 指針相等，且都指向下標為 0 的位置，隊列為空隊列。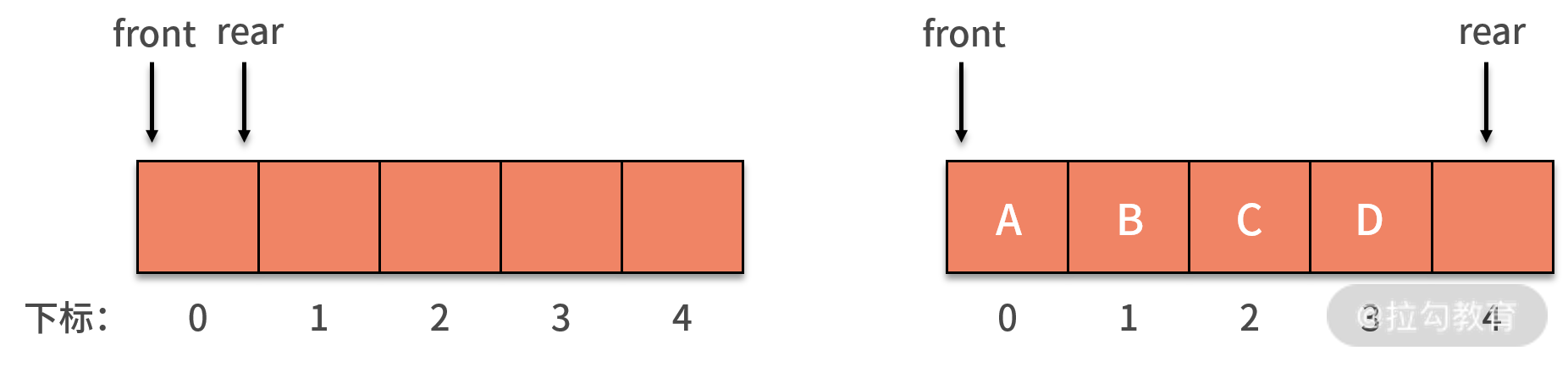如下圖所示：  當 A、B、C、D 四條數據加入隊列后，front 依然指向下標為 0 的位置，而 rear 則指向下標為 4 的位置。 當 A 出隊列時，front 指針指向下標為 1 的位置，rear 保持不變。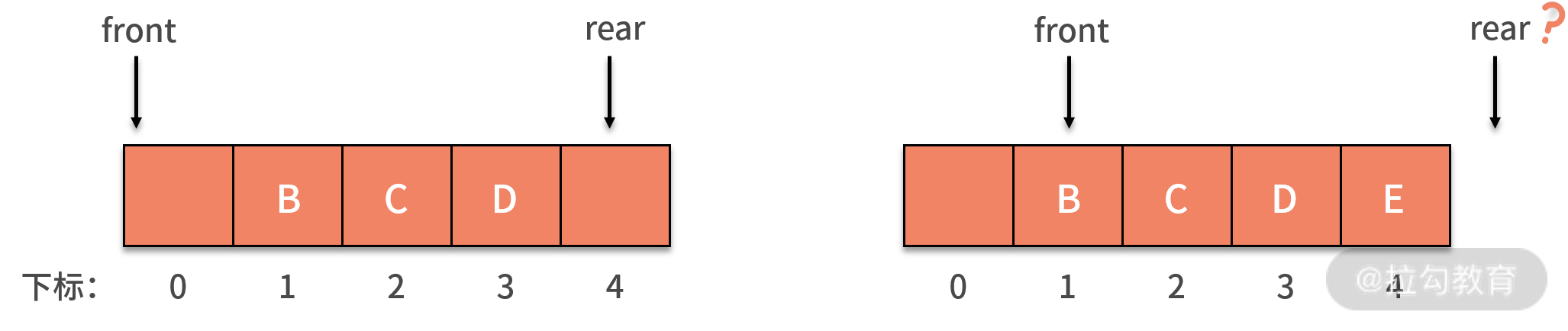其后 E 加入隊列，front 保持不變，rear 則移動到了數組以外，如下圖所示：  假設這個列隊的總個數不超過 5 個，但是目前繼續接著入隊，因為數組末尾元素已經被占用，再向后加，就會產生我們前面提到的數組越界問題。而實際上，我們列隊的下標 0 的地方還是空閑的，這就產生了一種 “假溢出” 的現象。 這種問題在采用順序存儲的隊列時，是一定要小心注意的。兩個簡單粗暴的解決方法就是： * 不惜消耗 O(n) 的時間復雜度去移動數據； * 或者開辟足夠大的內存空間確保數組不會越界。 #### 循環隊列的數據操作 很顯然上面的兩個方法都不太友好。其實，數組越界問題可以通過隊列的一個特殊變種來解決，叫作循環隊列。 循環隊列進行新增數據元素操作時，首先判斷隊列是否為滿。如果不滿，則可以將新元素賦值給隊尾，然后讓 rear 指針向后移動一個位置。如果已經排到隊列最后的位置，則 rea r指針重新指向頭部。 循環隊列進行刪除操作時，即出隊列操作，需要判斷隊列是否為空，然后將隊頭元素賦值給返回值，front 指針向后移一個位置。如果已經排到隊列最后的位置，就把 front 指針重新指向到頭部。這個過程就好像鐘表的指針轉到了表盤的尾部 12 點的位置后，又重新回到了表盤頭部 1 點鐘的位置。這樣就能在不開辟大量存儲空間的前提下，不采用 O(n) 的操作，也能通過移動數據來完成頻繁的新增和刪除數據。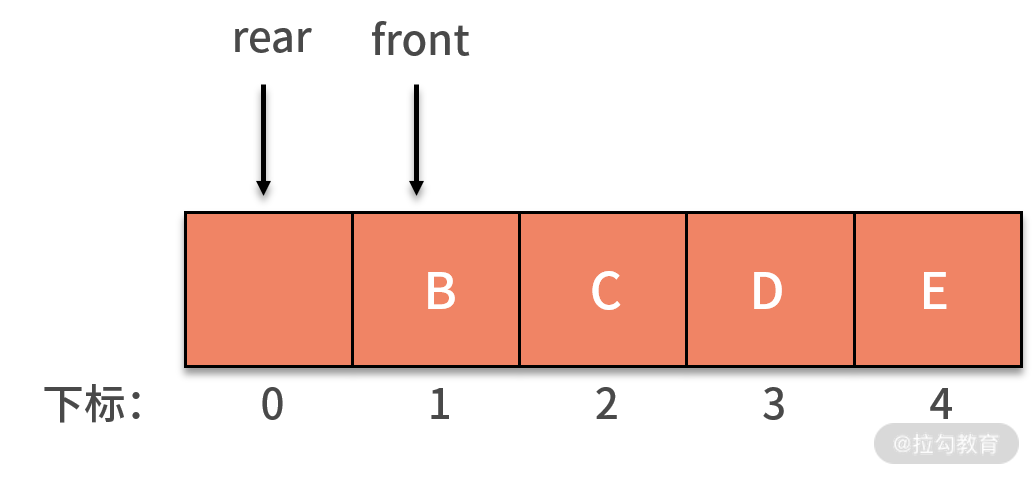 我們繼續回到前面提到的例子中，如果是循環隊列，rear 指針就可以重新指向下標為 0 的位置，如下圖所示：  如果這時再新增了 F 進入隊列，就可以放入在下標為 0 的位置，rear 指針指向下標為 1 的位置。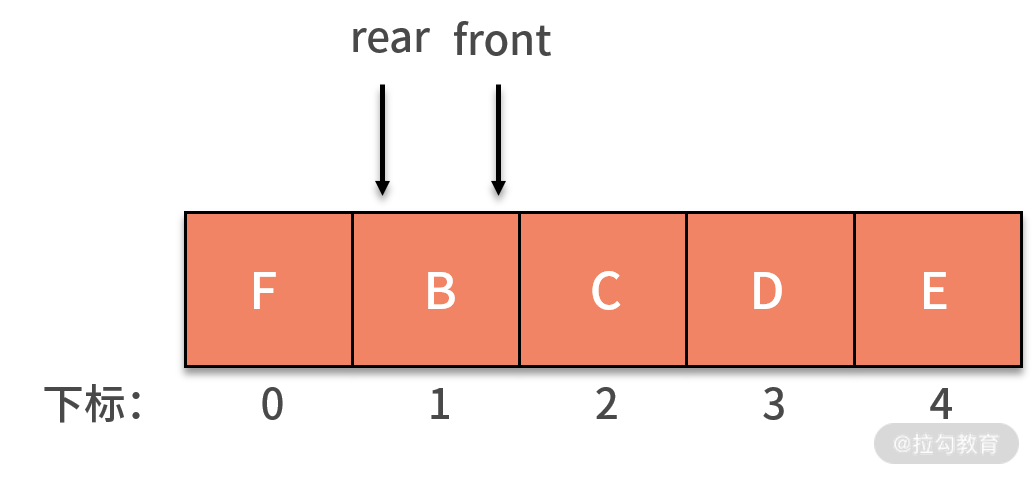這時的 rear 和 front 指針就會重合，指向下標為 1 的位置，如下圖所示：  此時，又會產生新的問題，即當隊列為空時，有 front 指針和 rear 指針相等。而現在的隊列是滿的，同樣有 front 指針和 rear 指針相等。那么怎樣判斷隊列到底是空還是滿呢？常用的方法是，設置一個標志變量 flag 來區別隊列是空還是滿。 * [ ] 鏈式隊列的數據操作 我們再看一下鏈式隊列的數據操作。鏈式隊列就是一個單鏈表，同時增加了 front 指針和 rear 指針。鏈式隊列和單鏈表一樣，通常會增加一個頭結點，并另 front 指針指向頭結點。頭結點不存儲數據，只是用來輔助標識。 鏈式隊列進行新增數據操作時，將擁有數值 X 的新結點 s 賦值給原隊尾結點的后繼，即 rear.next。然后把當前的 s 設置為隊尾結點，指針 rear 指向 s。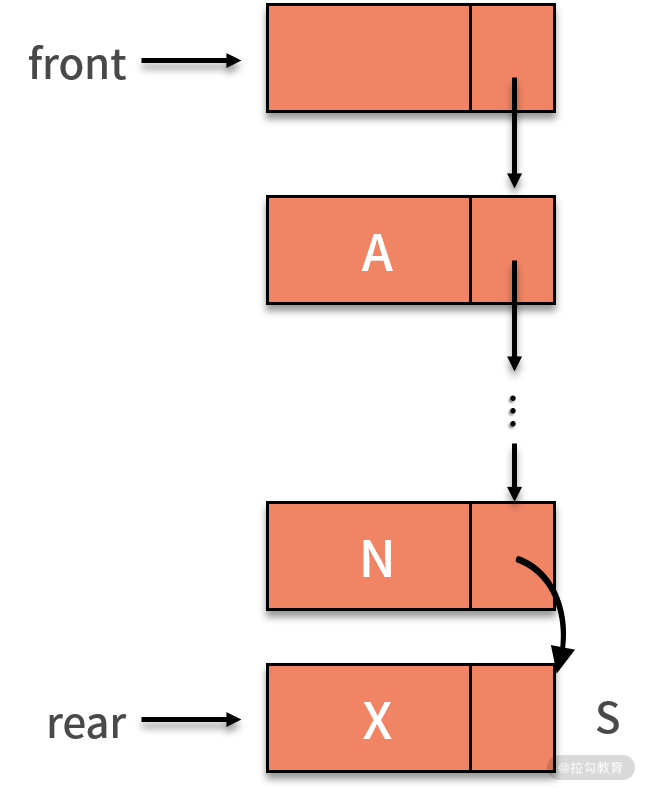如下圖所示：  當鏈式隊列進行刪除數據操作時，實際刪除的是頭結點的后繼結點。這是因為頭結點僅僅用來標識隊列，并不存儲數據。因此，出隊列的操作，就需要找到頭結點的后繼，這就是要刪除的結點。接著，讓頭結點指向要刪除結點的后繼。 特別值得一提的是，如果這個鏈表除去頭結點外只剩一個元素，那么刪除僅剩的一個元素后，rear 指針就變成野指針了。這時候，需要讓 rear 指針指向頭結點。也許你前面會對頭結點存在的意義產生懷疑，似乎沒有它也不影響增刪的操作。那么為何隊列還特被強調要有頭結點呢？ 這主要是為了防止刪除最后一個有效數據結點后， front 指針和 rear 指針變成野指針，導致隊列沒有意義了。有了頭結點后，哪怕隊列為空，頭結點依然存在，能讓 front 指針和 rear 指針依然有意義。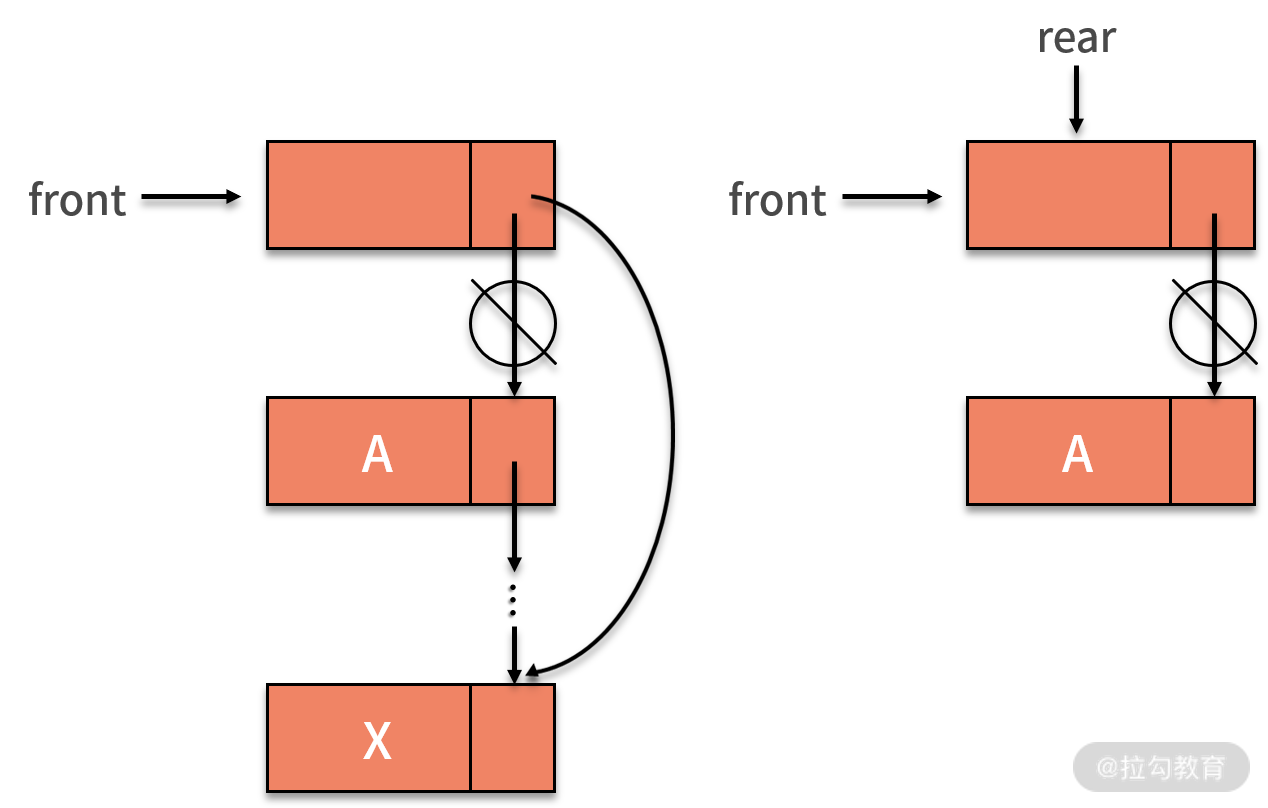  對于隊列的查找操作，不管是順序還是鏈式，隊列都沒有額外的改變。跟線性表一樣，它也需要遍歷整個隊列來完成基于某些條件的數值查找。因此時間復雜度也是 O(n)。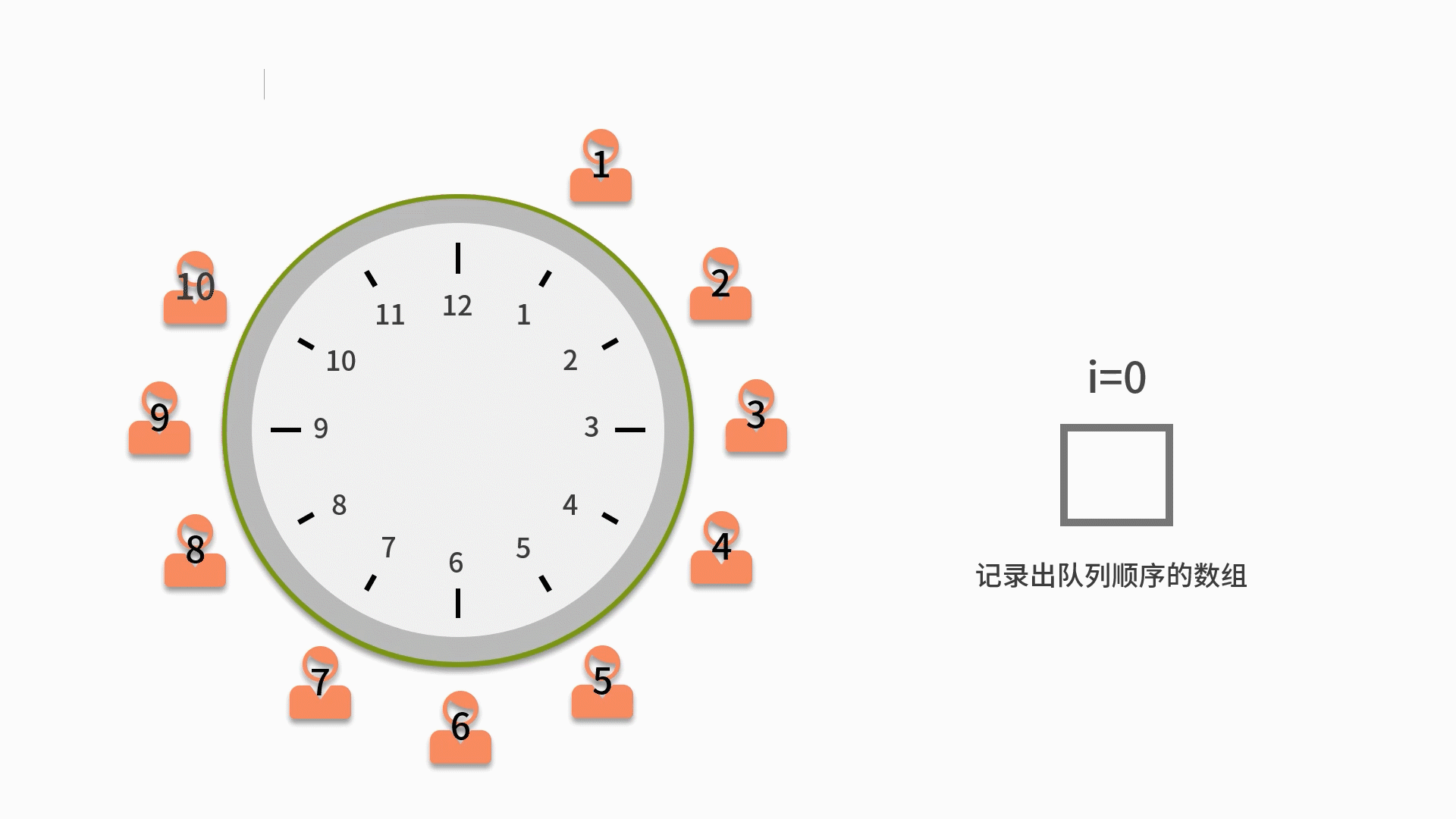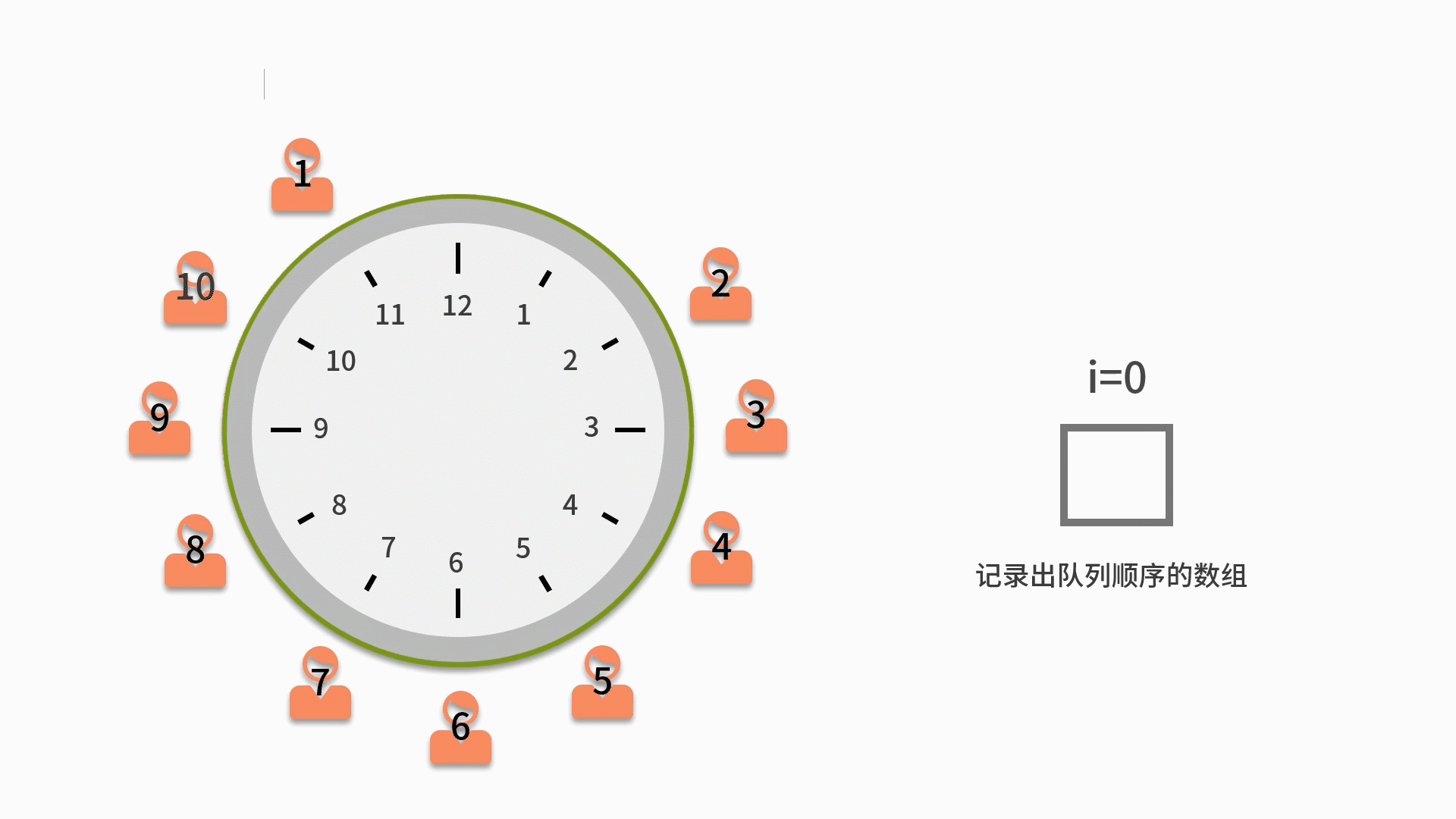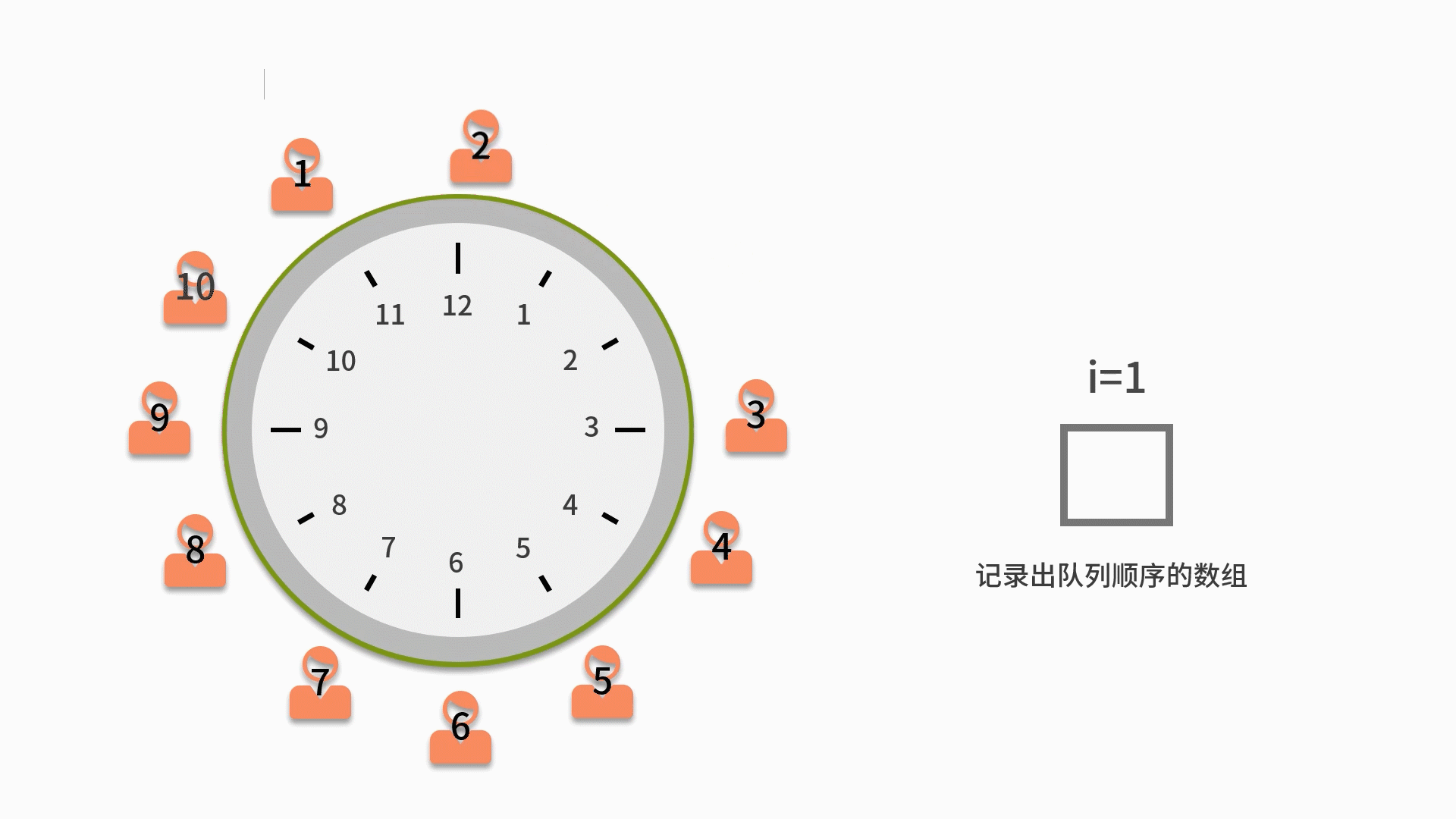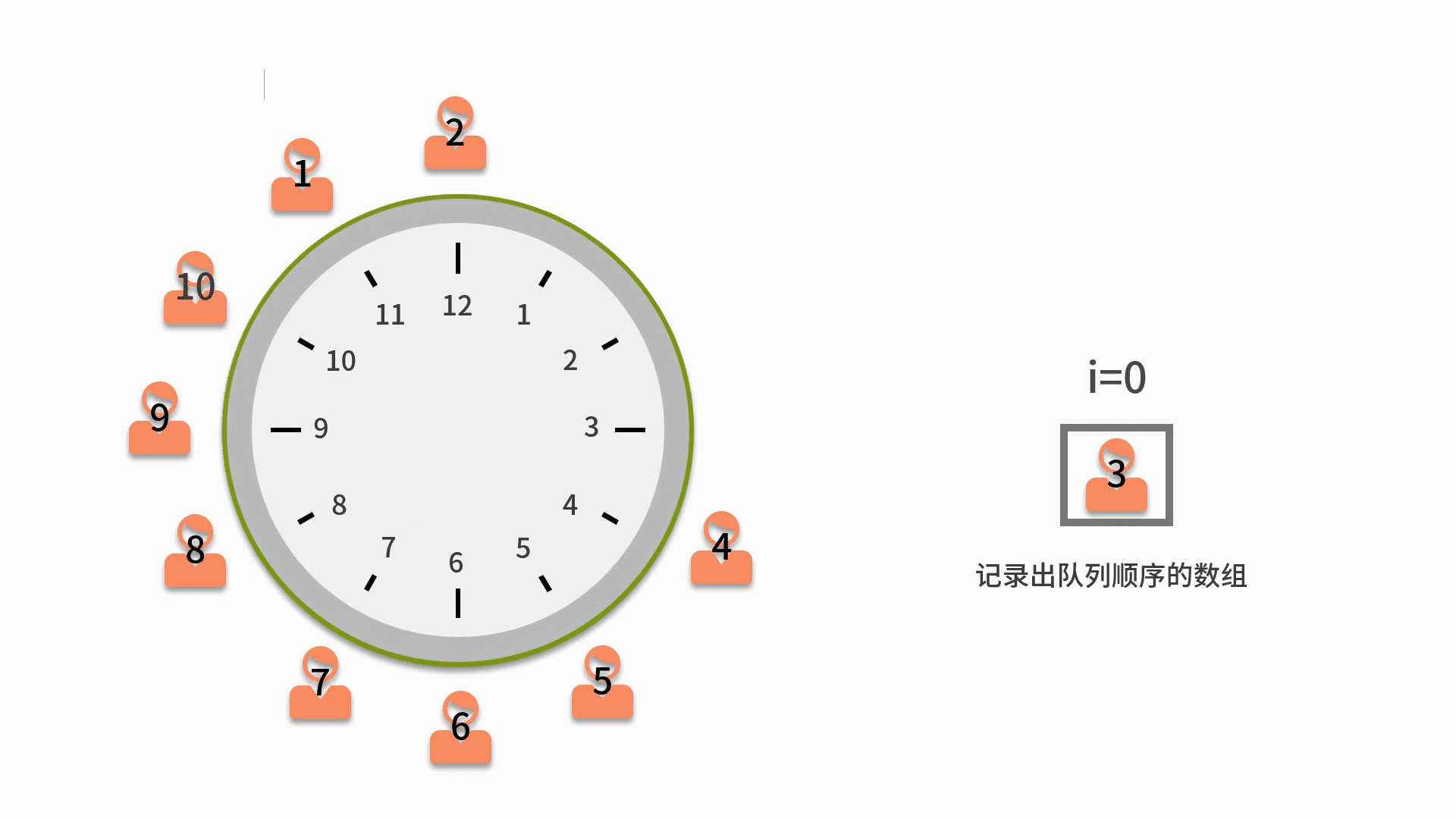 #### 隊列的案例 我們來看一個關于用隊列解決約瑟夫環問題。約瑟夫環是一個數學的應用問題，具體為，已知 n 個人（以編號 1，2，3...n 分別表示）圍坐在一張圓桌周圍。從編號為 k 的人開始報數，數到 m 的那個人出列；他的下一個人又從 1 開始報數，數到 m 的那個人又出列；依此規律重復下去，直到圓桌周圍的人全部出列。這個問題的輸入變量就是 n 和 m，即 n 個人和數到 m 的出列的人。輸出的結果，就是 n 個人出列的順序。 這個問題，用隊列的方法實現是個不錯的選擇。它的結果就是出列的順序，恰好滿足隊列對處理順序敏感的前提。因此，求解方式也是基于隊列的先進先出原則。解法如下： 1. 先把所有人都放入循環隊列中。注意這個循環隊列的長度要大于或者等于 n。 2. 從第一個人開始依次出隊列，出隊列一次則計數變量 i 自增。如果 i 比 m 小，則還需要再入隊列。 3. 直到i等于 m 的人出隊列時，就不用再讓這個人進隊列了。而是放入一個用來記錄出隊列順序的數組中。 4. 直到數完 n 個人為止。當隊列為空時，則表示隊列中的 n 個人都出隊列了，這時結束隊列循環，輸出數組內記錄的元素。 至此，我們就通過循環隊列解決了約瑟夫環問題。代碼如下：  ``` public static void main(String[] args) { ring(10, 5); } public static void ring(int n, int m) { LinkedList<Integer> q = new LinkedList<Integer>(); for (int i = 1; i <= n; i++) { q.add(i); } int k = 2; int element = 0; int i = 0; for (; i<k; i++) { element = q.poll(); q.add(element); } i = 1; while (q.size() > 0) { element = q.poll(); if (i < m) { q.add(element); i++; } else { i = 1; System.out.println(element); } } } ``` #### 總結 好的，這一節的內容就到這里了。本節課我們介紹了隊列的基本原理和隊列對于數據的增刪查的操作。可以發現，隊列與前一課時我們學習的棧的特性非常相似，隊列也繼承了線性表的優點與不足，是加了限制的線性表，隊列的增和刪的操作只能在這個線性表的頭和尾進行。 在時間復雜度上，循環隊列和鏈式隊列的新增、刪除操作都為 O(1)。而在查找操作中，隊列和線性表一樣只能通過全局遍歷的方式進行，也就是需要 O(n) 的時間復雜度。在空間性能方面，循環隊列必須有一個固定的長度，因此存在存儲元素數量和空間的浪費問題，而鏈式隊列不存在這種問題，所以在空間上，鏈式隊列更為靈活一些。 通常情況下，在可以確定隊列長度最大值時，建議使用循環隊列。無法確定隊列長度時，應考慮使用鏈式隊列。隊列具有先進先出的特點，很像現實中人們排隊買票的場景。在面對數據處理順序非常敏感的問題時，隊列一定是個不錯的技術選型。 如果你在隊列的使用方面遇到困難，歡迎在留言區和我交流。