在前面課時中，我們先后學習了線性表、數組、字符串和樹，并著重分析了它們對于數據的增刪查操作。 對于數據處理它們彼此之間各有千秋，例如： * 線性表中的棧和隊列對增刪有嚴格要求，它們會更關注數據的順序。 * 數組和字符串需要保持數據類型的統一，并且在基于索引的查找上會更有優勢。 * 樹的優勢則體現在數據的層次結構上。 但它們普遍都存在這樣的缺陷，那就是數據數值條件的查找，都需要對全部數據或者部分數據進行遍歷。那么，有沒有一種方法可以省去數據比較的過程，從而進一步提升數值條件查找的效率呢？答案當然是：有。這一課時我們就來介紹這樣一種高效率的查找神器，哈希表。 #### 什么是哈希表 哈希表名字源于 Hash，也可以叫作散列表。哈希表是一種特殊的數據結構，它與數組、鏈表以及樹等我們之前學過的數據結構相比，有很明顯的區別。 * [ ] 哈希表的核心思想 在我們之前學過的數據結構里，數據的存儲位置和數據的具體數值之間不存在任何關系。因此，在面對查找問題時，這些數據結構必須采取逐一比較的方法去實現。 而哈希表的設計采用了函數映射的思想，將記錄的存儲位置與記錄的關鍵字關聯起來。這樣的設計方式，能夠快速定位到想要查找的記錄，而且不需要與表中存在的記錄的關鍵字比較后再來進行查找。 我們回顧一下數組的查找操作。數組是通過數據的索引（index）來取出數值的，例如要找出 a 數組中，索引值為 1 的元素。在前面的課時中，我們講到索引值是數據存儲的位置，因此，直接通過 a[1] 就可以取出這個數據。通過這樣的方式，數組實現了“地址 = f (index)”的映射關系。 如果用哈希表的邏輯來理解的話，這里的 f () 就是一個哈希函數。它完成了索引值到實際地址的映射，這就讓數組可以快速完成基于索引值的查找。然而，數組的局限性在于，它只能基于數據的索引去查找，而不能基于數據的數值去查找。 如果有一種方法，可以實現“地址 = f (關鍵字)”的映射關系，那么就可以快速完成基于數據的數值的查找了。這就是哈希表的核心思想。 下面我們通過一個例子來體會一下。 假如，我們要對一個手機通訊錄進行存儲，并要根據姓名找出一個人的手機號碼，如下所示： ``` 張一：155555555 張二：166666666 張三：177777777 張四：188888888 ``` 一個可行的方法是，定義包含姓名、手機號碼的結構體，再通過鏈表把 4 個聯系人的信息存起來。當要判斷“張四”是否在鏈表中，或者想要查找到張四的手機號碼時，就需要從鏈表的頭結點開始遍歷。依次將每個結點中的姓名字段，同“張四”進行比較。直到查找成功或者全部遍歷一次為止。顯然，這種做法的時間復雜度為 O(n)。 如果要降低時間復雜度，就需要借助哈希表的思路，構建姓名到地址的映射函數“地址 = f (姓名)”。這樣，我們就可以通過這個函數直接計算出”張四“的存儲位置，在 O(1) 時間復雜度內就可以完成數據的查找。 通過這個例子，不難看出 Hash 函數設計的好壞會直接影響到對哈希表的操作效率。假如對上面的例子采用的 Hash 函數為，姓名的每個字的拼音開頭大寫字母的 ASCII 碼之和。即： ``` address (張一) = ASCII (Z) + ASCII (Y) = 90 + 89 = 179； address (張二) = ASCII (Z) + ASCII (E) = 90 + 69 = 159； address (張三) = ASCII (Z) + ASCII (S) = 90 + 83 = 173； address (張四) = ASCII (Z) + ASCII (S) = 90 + 83 = 173； ``` 我們發現這個哈希函數存在一個非常致命的問題，那就是 f ( 張三) 和 f (張四) 都是 173。這種現象稱作哈希沖突，是需要在設計哈希函數時進行規避的。 從本質上來看，哈希沖突只能盡可能減少，不能完全避免。這是因為，輸入數據的關鍵字是個開放集合。只要輸入的數據量夠多、分布夠廣，就完全有可能發生沖突的情況。因此，哈希表需要設計合理的哈希函數，并且對沖突有一套處理機制。 * [ ] 如何設計哈希函數 我們先看一些常用的設計哈希函數的方法： * 第一，直接定制法 哈希函數為關鍵字到地址的線性函數。如，H (key) = a*key + b。?這里，a 和 b 是設置好的常數。 * 第二，數字分析法 假設關鍵字集合中的每個關鍵字 key 都是由 s 位數字組成（k1,k2,…,Ks），并從中提取分布均勻的若干位組成哈希地址。上面張一、張二、張三、張四的手機號信息存儲，就是使用的這種方法。 * 第三，平方取中法 如果關鍵字的每一位都有某些數字重復出現，并且頻率很高，我們就可以先求關鍵字的平方值，通過平方擴大差異，然后取中間幾位作為最終存儲地址。 * 第四，折疊法 如果關鍵字的位數很多，可以將關鍵字分割為幾個等長的部分，取它們的疊加和的值（舍去進位）作為哈希地址。 * 第五，除留余數法 預先設置一個數 p，然后對關鍵字進行取余運算。即地址為 key mod p。 * [ ] 如何解決哈希沖突 上面這些常用方法都有可能會出現哈希沖突。那么一旦發生沖突，我們該如何解決呢？ 常用的方法，有以下兩種： * 第一，開放定址法 即當一個關鍵字和另一個關鍵字發生沖突時，使用某種探測技術在哈希表中形成一個探測序列，然后沿著這個探測序列依次查找下去。當碰到一個空的單元時，則插入其中。 常用的探測方法是線性探測法。 比如有一組關鍵字 {12，13，25，23}，采用的哈希函數為 key mod 11。當插入 12，13，25 時可以直接插入，地址分別為 1、2、3。而當插入 23 時，哈希地址為 23 mod 11 = 1。然而，地址 1 已經被占用，因此沿著地址 1 依次往下探測，直到探測到地址 4，發現為空，則將 23 插入其中。如下圖所示：  * 第二，鏈地址法 將哈希地址相同的記錄存儲在一張線性鏈表中。 例如，有一組關鍵字 {12,13,25,23,38,84,6,91,34}，采用的哈希函數為 key mod 11。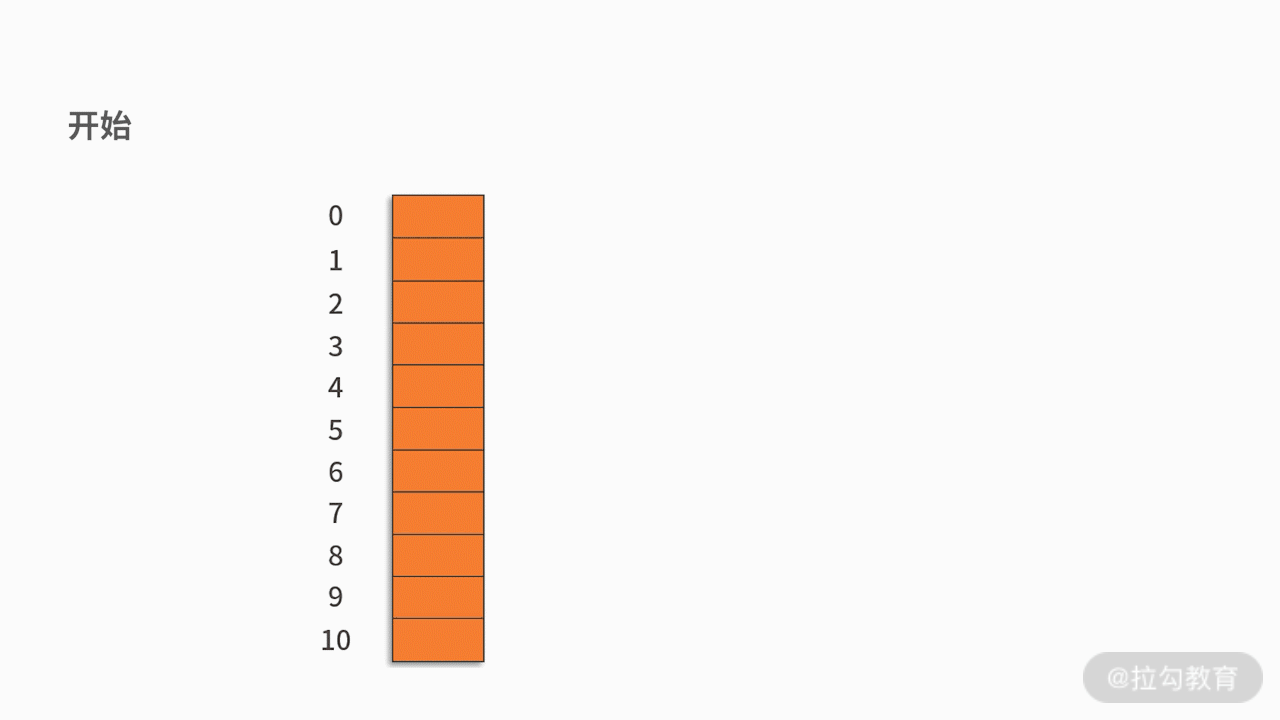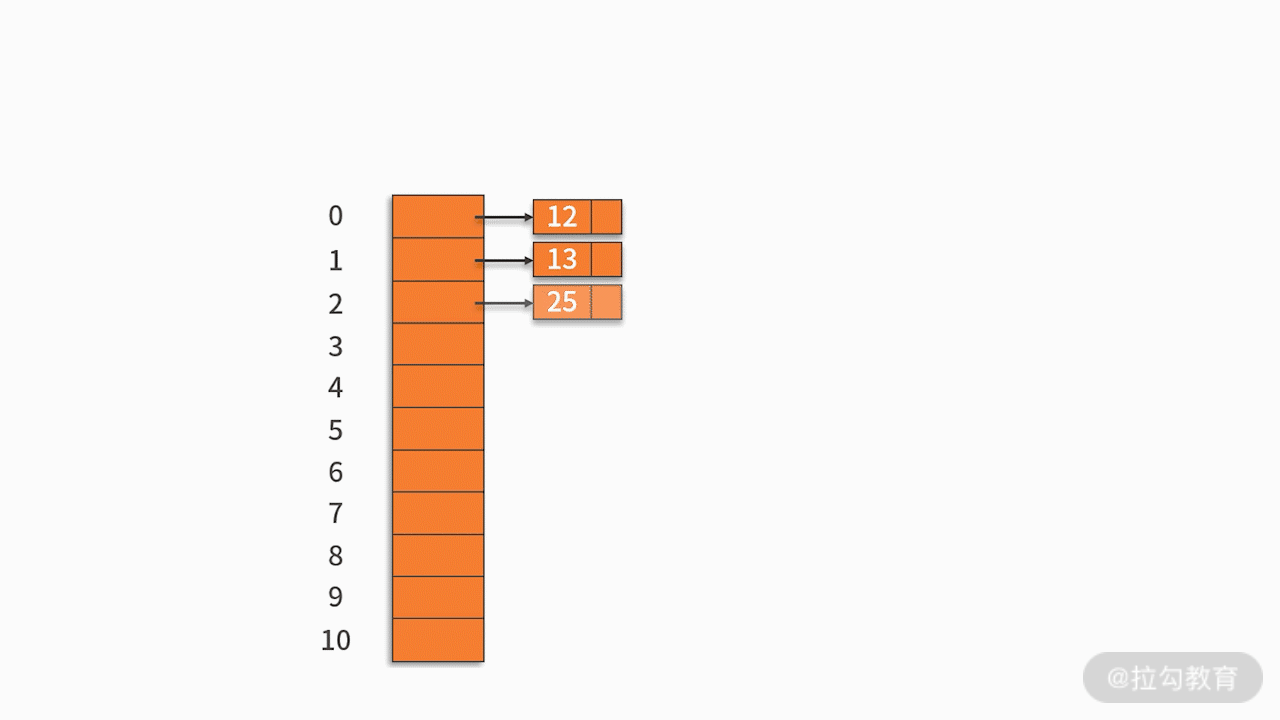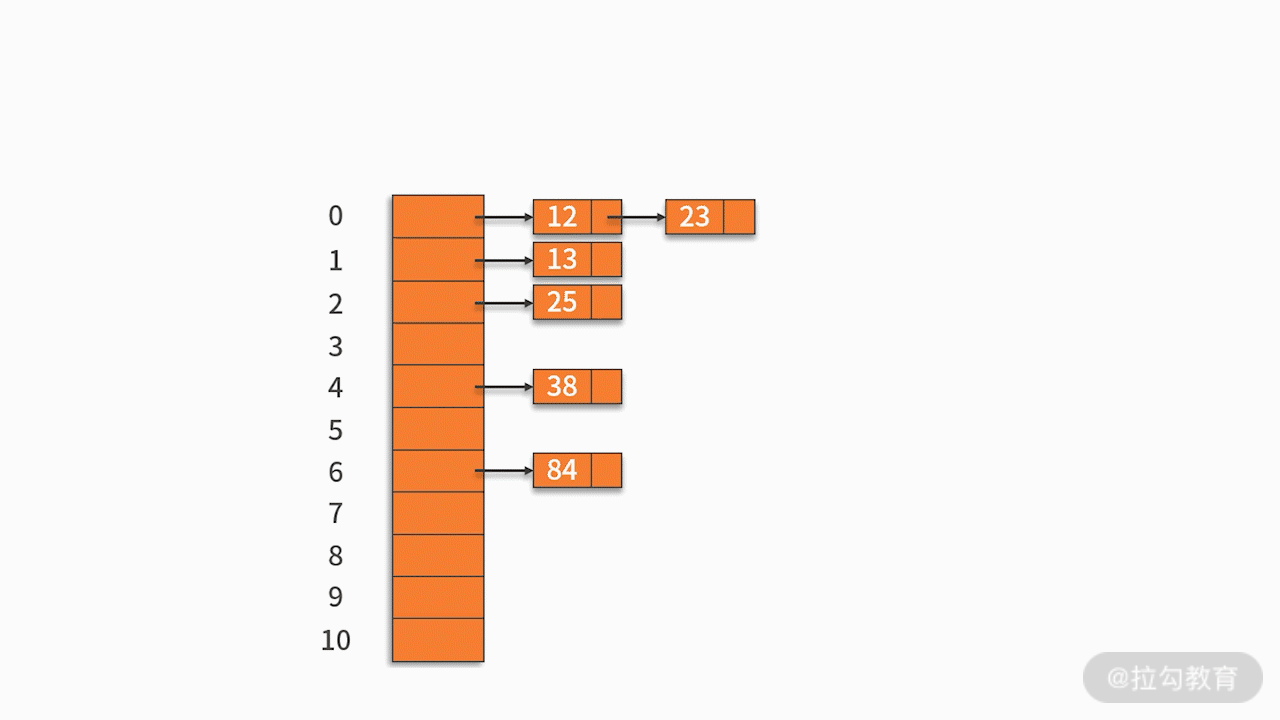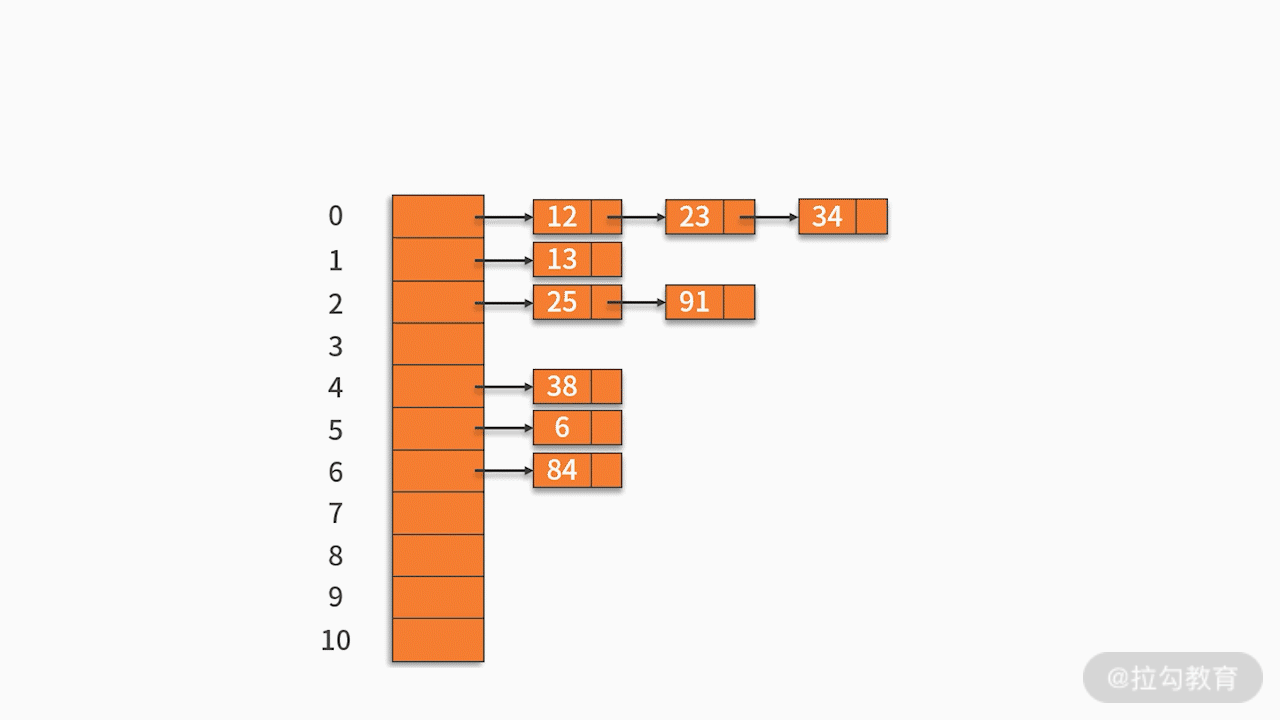如下圖所示：  哈希表相對于其他數據結構有很多的優勢。它可以提供非常快速的插入-刪除-查找操作，無論多少數據，插入和刪除值需要接近常量的時間。在查找方面，哈希表的速度比樹還要快，基本可以瞬間查找到想要的元素。 哈希表也有一些不足。哈希表中的數據是沒有順序概念的，所以不能以一種固定的方式（比如從小到大）來遍歷其中的元素。在數據處理順序敏感的問題時，選擇哈希表并不是個好的處理方法。同時，哈希表中的 key 是不允許重復的，在重復性非常高的數據中，哈希表也不是個好的選擇。 #### 哈希表的基本操作 在很多高級語言中，哈希函數、哈希沖突都已經在底層完成了黑盒化處理，是不需要開發者自己設計的。也就是說，哈希表完成了關鍵字到地址的映射，可以在常數級時間復雜度內通過關鍵字查找到數據。 至于實現細節，比如用了哪個哈希函數，用了什么沖突處理，甚至某個數據記錄的哈希地址是多少，都是不需要開發者關注的。接下來，我們從實際的開發角度，來看一下哈希表對數據的增刪查操作。 哈希表中的增加和刪除數據操作，不涉及增刪后對數據的挪移問題（數組需要考慮），因此處理就可以了。 哈希表查找的細節過程是：對于給定的 key，通過哈希函數計算哈希地址 H (key)。 * 如果哈希地址對應的值為空，則查找不成功。 * 反之，則查找成功。 雖然哈希表查找的細節過程還比較麻煩，但因為一些高級語言的黑盒化處理，開發者并不需要實際去開發底層代碼，只要調用相關的函數就可以了。 #### 哈希表的案例 下面我們來講解兩個案例，幫助你進一步理解哈希表的操作過程。 例 1，將關鍵字序列 {7, 8, 30, 11, 18, 9, 14} 存儲到哈希表中。哈希函數為： H (key) = (key * 3) % 7，處理沖突采用線性探測法。 接下來，我們分析一下建立哈希表和查找關鍵字的細節過程。 首先，我們嘗試建立哈希表，求出這個哈希地址： ``` H (7) = (7 * 3) % 7 = 0 H (8) = (8 * 3) % 7 = 3 H (30) = 6 H (11) = 5 H (18) = 5 H (9) = 6 H (14) = 0 ``` 按關鍵字序列順序依次向哈希表中填入，發生沖突后按照“線性探測”探測到第一個空位置填入。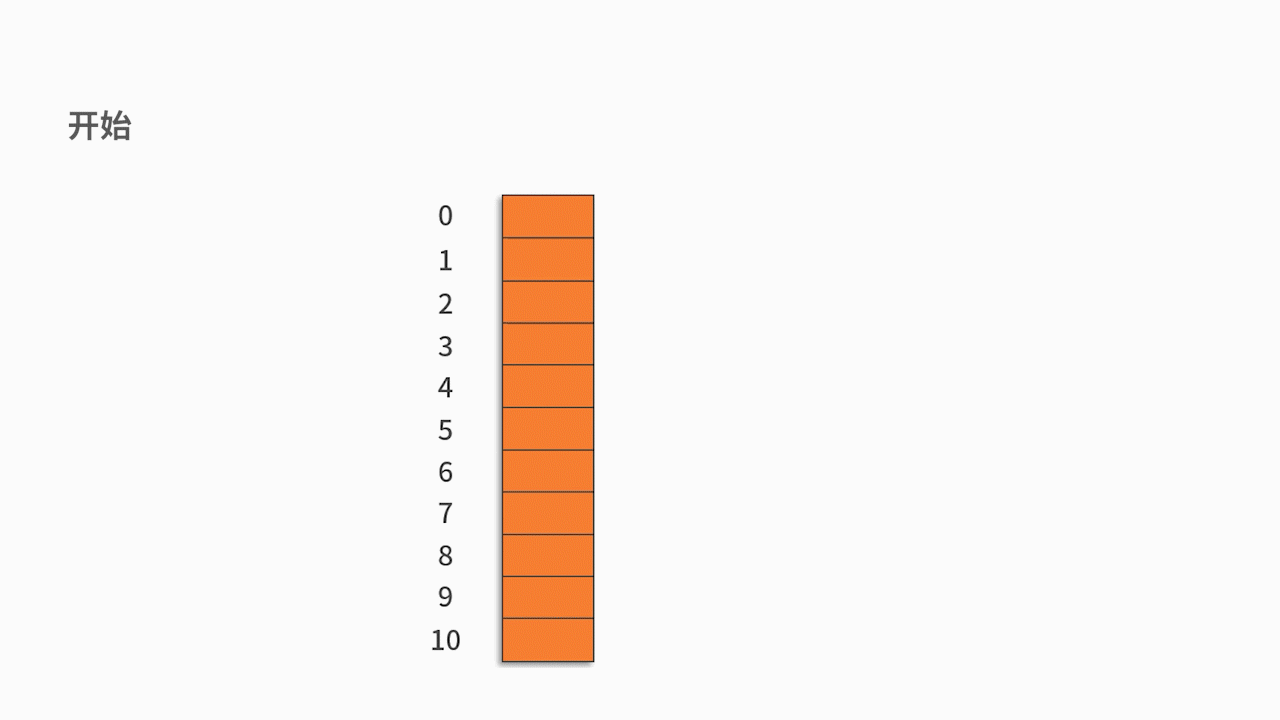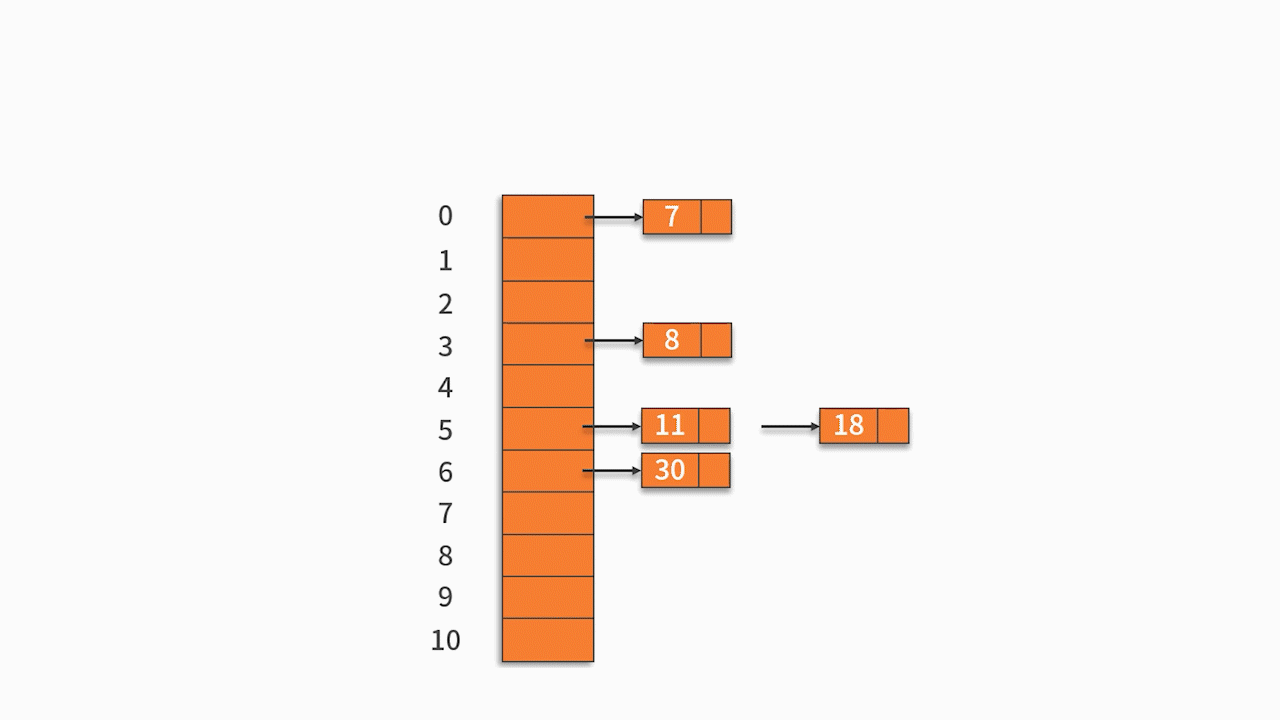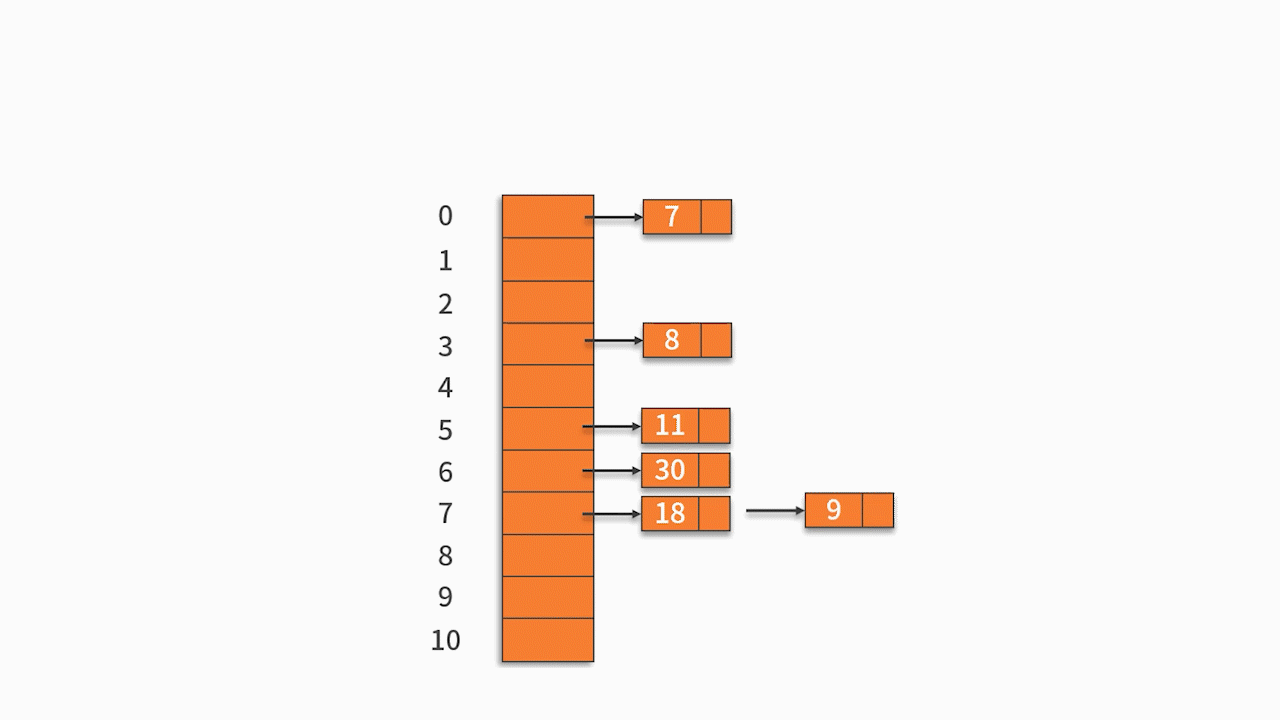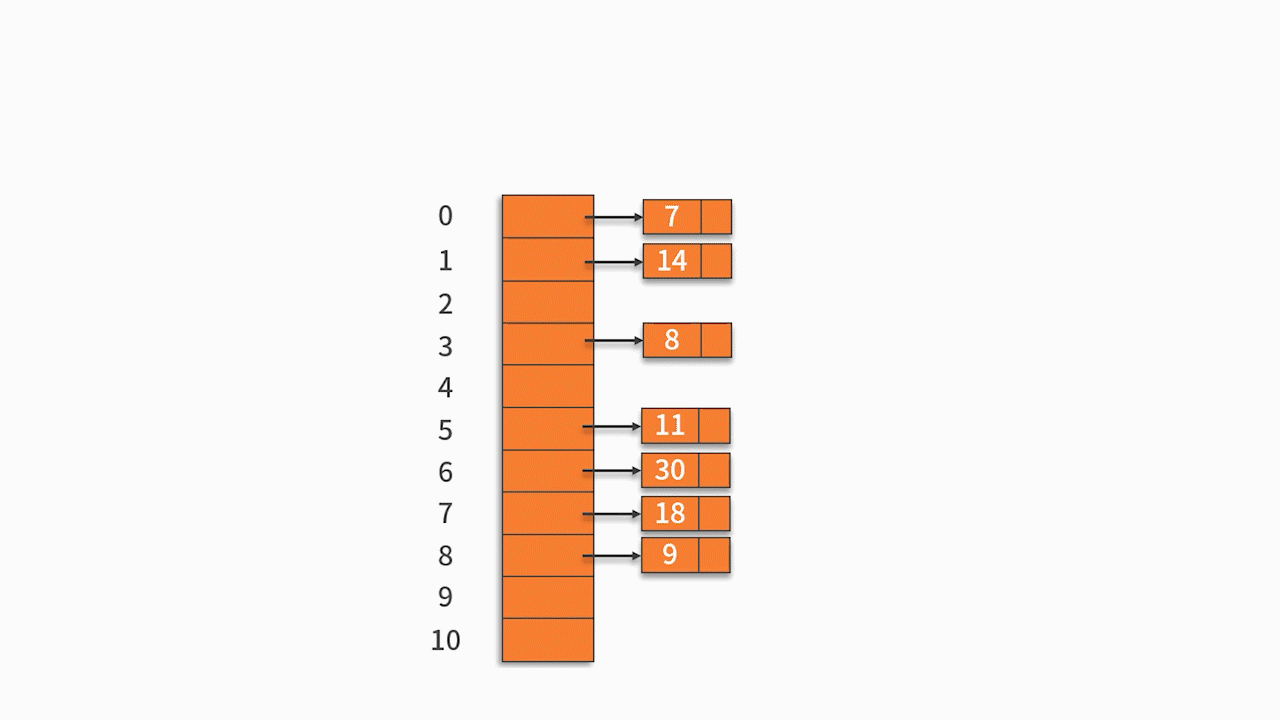  最終的插入結果如下表所示：  接著，有了這個表之后，我們再來看一下查找的流程： * 查找 7。輸入 7，計算得到 H (7) = 0，根據哈希表，在 0 的位置，得到結果為 7，跟待匹配的關鍵字一樣，則完成查找。 * 查找 18。輸入 18，計算得到 H (18) = 5，根據哈希表，在 5 的位置，得到結果為 11，跟待匹配的關鍵字不一樣（11 不等于 18）。因此，往后挪移一位，在 6 的位置，得到結果為 30，跟待匹配的關鍵字不一樣（11 不等于 30）。因此，繼續往后挪移一位，在 7 的位置，得到結果為 18，跟待匹配的關鍵字一樣，完成查找。 例 2，假設有一個在線系統，可以實時接收用戶提交的字符串型關鍵字，并實時返回給用戶累積至今這個關鍵字被提交的次數。 例如，用戶輸入"abc"，系統返回 1。用戶再輸入"jk"，系統返回 1。用戶再輸入"xyz"，系統返回 1。用戶再輸入"abc"，系統返回 2。用戶再輸入"abc"，系統返回 3。 一種解決方法是，用一個數組保存用戶提交過的所有關鍵字。當接收到一個新的關鍵字后，插入到數組中，并且統計這個關鍵字出現的次數。 根據數組的知識可以計算出，插入到最后的動作，時間復雜度是 O(1)。但統計出現次數必須要全部數據遍歷一遍，時間復雜度是 O(n)。隨著數據越來越多，這個在線系統的處理時間將會越來越長。顯然，這不是一個好的方法。 如果采用哈希表，則可以利用哈希表新增、查找的常數級時間復雜度，在 O(1) 時間復雜度內完成響應。預先定義好哈希表后（可以采用 Map < String, Integer > d = new HashMap <> (); ）對于關鍵字（用變量 key_str 保存），判斷 d 中是否存在 key_str 的記錄。 * 如果存在，則把它對應的value（用來記錄出現的頻次）加 1； * 如果不存在，則把它添加到 d 中，對應的 value 賦值為 1。最后，打印處 key_str 對應的 value，即累積出現的頻次。 代碼如下： ``` if (d.containsKey(key_str) { d.put(key_str, d.get(key_str) + 1); } else{ d.put(key_str, 1); } System.out.println(d.get(key_str)); ``` #### 總結 哈希表在我們平時的數據處理操作中有著很多獨特的優點，不論哈希表中有多少數據，查找、插入、刪除只需要接近常量的時間，即 O(1）的時間級。 實際上，這只需要幾條機器指令。哈希表運算得非常快，在計算機程序中，如果需要在一秒鐘內查找上千條記錄通常使用哈希表（例如拼寫檢查器)，哈希表的速度明顯比樹快，樹的操作通常需要 O(n) 的時間級。哈希表不僅速度快，編程實現也相對容易。如果不需要有序遍歷數據，并且可以提前預測數據量的大小。那么哈希表在速度和易用性方面是無與倫比的。 #### 練習題 下面，我們給出一道練習題。這個問題是力扣的經典問題，two sums。給定一個整數數組 arr 和一個目標值 target，請你在該數組中找出加和等于目標值的那兩個整數，并返回它們的在數組中下標。 你可以假設，原數組中沒有重復元素，而且有且只有一組答案。但是，數組中的元素只能使用一次。例如，arr = [1, 2, 3, 4, 5, 6]，target = 4。因為，arr[0] + arr[2] = 1 + 3 = 4 = target，則輸出 0，2。 這道題目你可以采用暴力解法來完成，也可以使用哈希表提高效率。我們會在后續實戰課程給出詳細解法。