這一節我們來講字符串和它的相關操作。 #### 字符串是什么 字符串（string） 是由 n 個字符組成的一個有序整體（ n >= 0 ）。例如，s = "BEIJING" ，s 代表這個串的串名，BEIJING 是串的值。這里的雙引號不是串的值，作用只是為了將串和其他結構區分開。字符串的邏輯結構和線性表很相似，不同之處在于字符串針對的是字符集，也就是字符串中的元素都是字符，線性表則沒有這些限制。 在實際操作中，我們經常會用到一些特殊的字符串： * 空串，指含有零個字符的串。例如，s = ""，書面中也可以直接用 ? 表示。 * 空格串，只包含空格的串。它和空串是不一樣的，空格串中是有內容的，只不過包含的是空格，且空格串中可以包含多個空格。例如，s = "?? "，就是包含了 3 個空格的字符串。 * 子串，串中任意連續字符組成的字符串叫作該串的子串。 * 原串通常也稱為主串。例如：a = "BEI"，b = "BEIJING"，c = "BJINGEI" 。 * 對于字符串 a 和 b 來說，由于 b 中含有字符串 a ，所以可以稱 a 是 b 的子串，b 是 a 的主串； * 而對于 c 和 a 而言，雖然 c 中也含有 a 的全部字符，但不是連續的 "BEI" ，所以串 c 和 a 沒有任何關系。 當要判斷兩個串是否相等的時候，就需要定義相等的標準了。只有兩個串的串值完全相同，這兩個串才相等。根據這個定義可見，即使兩個字符串包含的字符完全一致，它們也不一定是相等的。例如 b = "BEIJING"，c = "BJINGEI"，則 b 和 c 并不相等。 字符串的存儲結構與線性表相同，也有順序存儲和鏈式存儲兩種。 * 字符串的順序存儲結構，是用一組地址連續的存儲單元來存儲串中的字符序列，一般是用定長數組來實現。有些語言會在串值后面加一個不計入串長度的結束標記符，比如 \0 來表示串值的終結。 * 字符串的鏈式存儲結構，與線性表是相似的，但由于串結構的特殊性（結構中的每個元素數據都是一個字符），如果也簡單地將每個鏈結點存儲為一個字符，就會造成很大的空間浪費。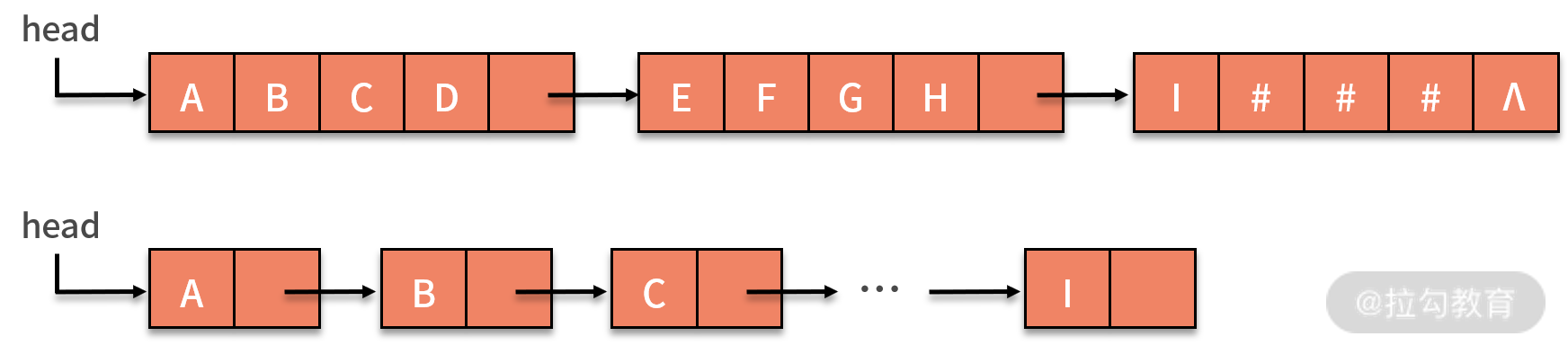因此，一個結點可以考慮存放多個字符，如果最后一個結點未被占滿時，可以使用 "#" 或其他非串值字符補全，如下圖所示：  在鏈式存儲中，每個結點設置字符數量的多少，與串的長度、可以占用的存儲空間以及程序實現的功能相關。 * 如果字符串中包含的數據量很大，但是可用的存儲空間有限，那么就需要提高空間利用率，相應地減少結點數量。 * 而如果程序中需要大量地插入或者刪除數據，如果每個節點包含的字符過多，操作字符就會變得很麻煩，為實現功能增加了障礙。 因此，串的鏈式存儲結構除了在連接串與串操作時有一定的方便之外，總的來說，不如順序存儲靈活，在性能方面也不如順序存儲結構好。 #### 字符串的基本操作 字符串和線性表的操作很相似，但由于字符串針對的是字符集，所有元素都是字符，因此字符串的基本操作與線性表有很大差別。線性表更關注的是單個元素的操作，比如增刪查一個元素，而字符串中更多關注的是查找子串的位置、替換等操作。接下來我們以順序存儲為例，詳細介紹一下字符串對于另一個字符串的增刪查操作。 * [ ] 字符串的新增操作 字符串的新增操作和數組非常相似，都牽涉對插入字符串之后字符的挪移操作，所以時間復雜度是 O(n)。 例如，在字符串 s1 = "123456" 的正中間插入 s2 = "abc"，則需要讓 s1 中的 "456" 向后挪移 3 個字符的位置，再讓 s2 的 "abc" 插入進來。很顯然，挪移的操作時間復雜度是 O(n)。不過，對于特殊的插入操作時間復雜度也可以降低為 O(1)。這就是在 s1 的最后插入 s2，也叫作字符串的連接，最終得到 "123456abc"。 * [ ] 字符串的刪除操作 字符串的刪除操作和數組同樣非常相似，也可能會牽涉刪除字符串后字符的挪移操作，所以時間復雜度是 O(n)。 例如，在字符串 s1 = "123456" 的正中間刪除兩個字符 "34"，則需要刪除 "34" 并讓 s1 中的 "56" 向前挪移 2 個字符的位置。很顯然，挪移的操作時間復雜度是 O(n)。不過，對于特殊的插入操作時間復雜度也可以降低為 O(1)。這就是在 s1 的最后刪除若干個字符，不牽涉任何字符的挪移。 * [ ] 字符串的查找操作 字符串的查找操作，是反映工程師對字符串理解深度的高頻考點，這里需要你格外注意。 例如，字符串 s = "goodgoogle"，判斷字符串 t = "google" 在 s 中是否存在。需要注意的是，如果字符串 t 的每個字符都在 s 中出現過，這并不能證明字符串 t 在 s 中出現了。當 t = "dog" 時，那么字符 "d"、"o"、"g" 都在 s 中出現過，但他們并不連在一起。 那么我們如何判斷一個子串是否在字符串中出現過呢？這個問題也被稱作子串查找或字符串匹配，接下來我們來重點分析。 * [ ] 子串查找（字符串匹配） 首先，我們來定義兩個概念，主串和模式串。我們在字符串 A 中查找字符串 B，則 A 就是主串，B 就是模式串。我們把主串的長度記為 n，模式串長度記為 m。由于是在主串中查找模式串，因此，主串的長度肯定比模式串長，n>m。因此，字符串匹配算法的時間復雜度就是 n 和 m 的函數。 假設要從主串 s = "goodgoogle" 中找到 t = "google" 子串。根據我們的思考邏輯，則有： * 首先，我們從主串 s 第 1 位開始，判斷 s 的第 1 個字符是否與 t 的第 1 個字符相等。 * 如果不相等，則繼續判斷主串的第 2 個字符是否與 t 的第1 個字符相等。直到在 s 中找到與 t 第一個字符相等的字符時，然后開始判斷它之后的字符是否仍然與 t 的后續字符相等。 * 如果持續相等直到 t 的最后一個字符，則匹配成功。 * 如果發現一個不等的字符，則重新回到前面的步驟中，查找 s 中是否有字符與 t 的第一個字符相等。 * 如下圖所示，s 的第1 個字符和 t 的第 1 個字符相等，則開始匹配后續。直到發現前三個字母都匹配成功，但 s 的第 4 個字母匹配失敗，則回到主串繼續尋找和 t 的第一個字符相等的字符。 * 如下圖所示，這時我們發現主串 s 第 5 位開始相等，并且隨后的 6 個字母全匹配成功，則找到結果。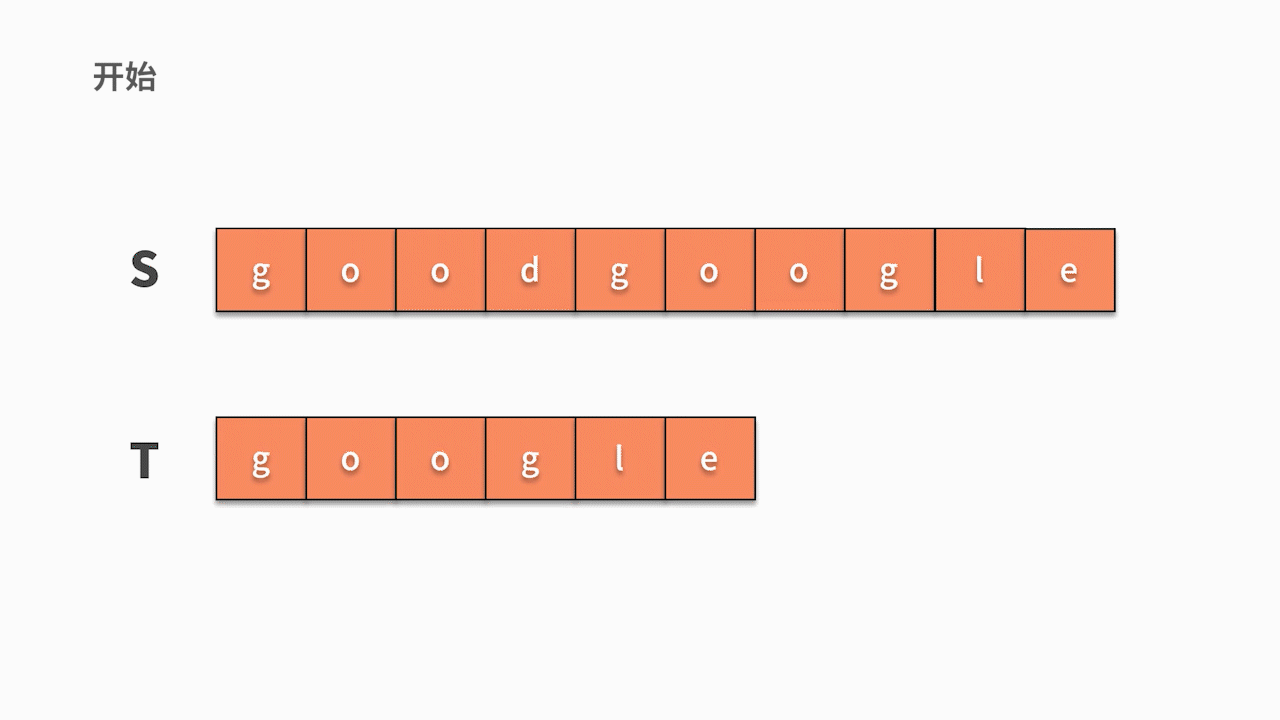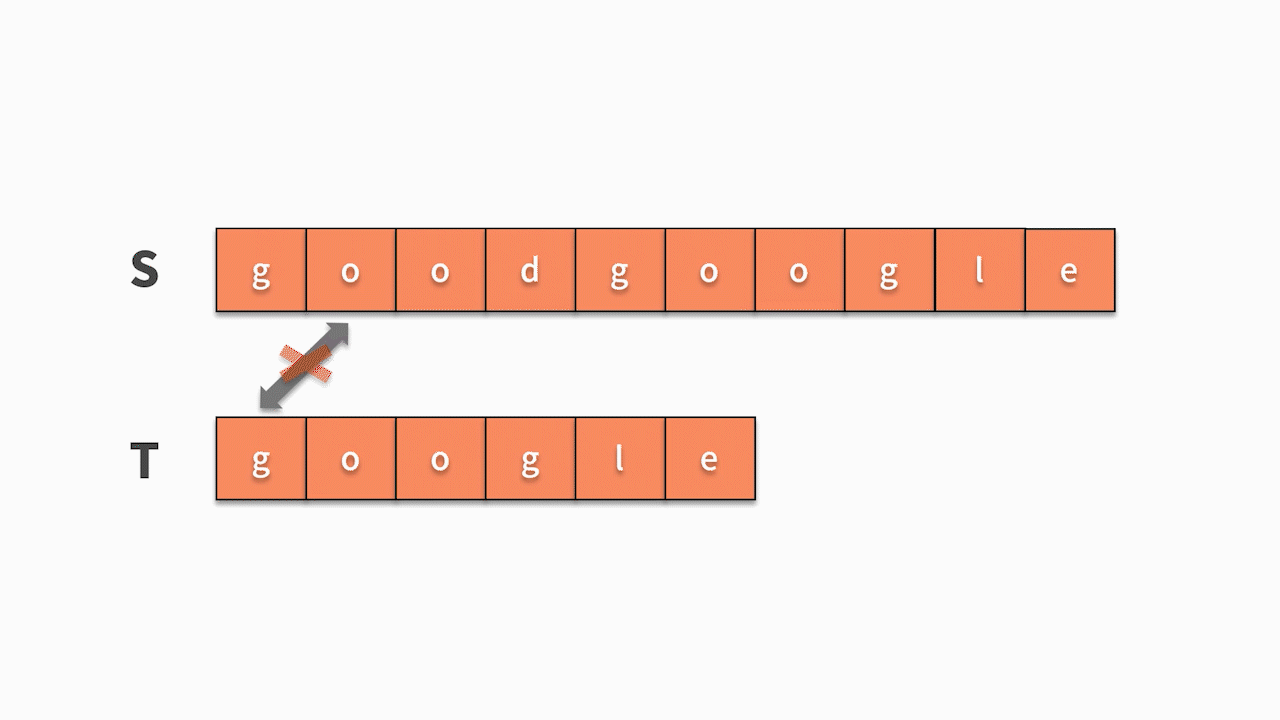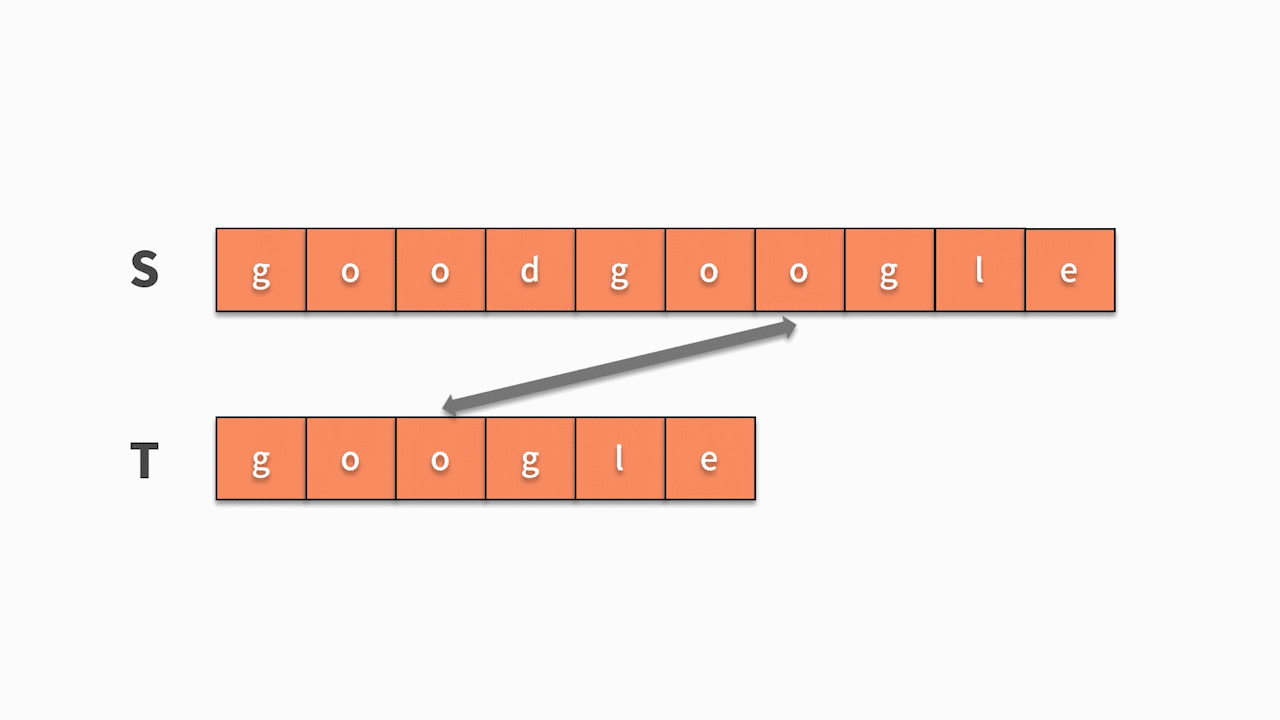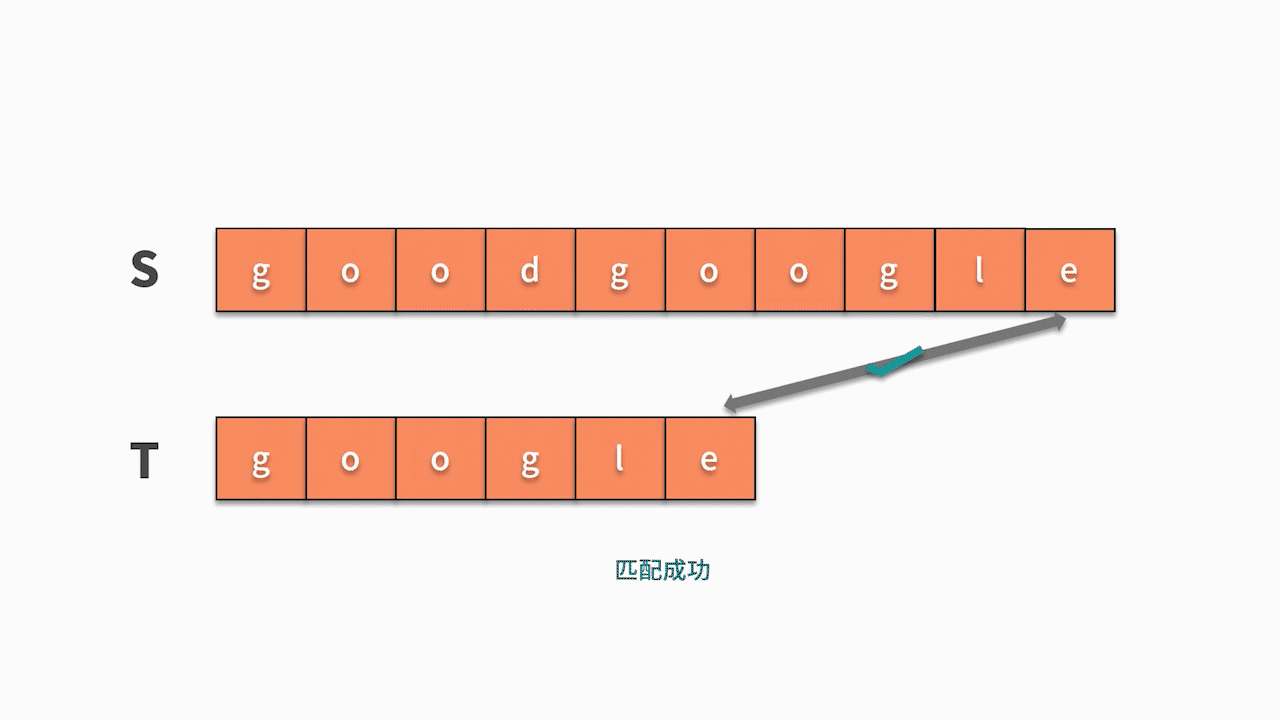  這種匹配算法需要從主串中找到跟模式串的第 1 個字符相等的位置，然后再去匹配后續字符是否與模式串相等。顯然，從實現的角度來看，需要兩層的循環。第一層循環，去查找第一個字符相等的位置，第二層循環基于此去匹配后續字符是否相等。因此，這種匹配算法的時間復雜度為 O(nm)。其代碼如下： ``` public void s1() { String s = "goodgoogle"; String t = "google"; int isfind = 0; for (int i = 0; i < s.length() - t.length() + 1; i++) { if (s.charAt(i) == t.charAt(0)) { int jc = 0; for (int j = 0; j < t.length(); j++) { if (s.charAt(i + j) != t.charAt(j)) { break; } jc = j; } if (jc == t.length() - 1) { isfind = 1; } } } System.out.println(isfind); } ``` #### 字符串匹配算法的案例 最后我們給出一道面試中常見的高頻題目，這也是對字符串匹配算法進行拓展，從而衍生出的問題，即查找出兩個字符串的最大公共字串。 假設有且僅有 1 個最大公共子串。比如，輸入 a = "13452439"， b = "123456"。由于字符串 "345" 同時在 a 和 b 中出現，且是同時出現在 a 和 b 中的最長子串。因此輸出 "345”。 對于這個問題其實可以用動態規劃的方法來解決，關于動態規劃，我們會在后續的課程會講到，所以在這里我們沿用前面的匹配算法。 假設字符串 a 的長度為 n，字符串 b 的長度為 m，可見時間復雜度是 n 和 m 的函數。 * 首先，你需要對于字符串 a 和 b 找到第一個共同出現的字符，這跟前面講到的匹配算法在主串中查找第一個模式串字符一樣。 * 然后，一旦找到了第一個匹配的字符之后，就可以同時在 a 和 b 中繼續匹配它后續的字符是否相等。這樣 a 和 b 中每個互相匹配的字串都會被訪問一遍。全局還要維護一個最長子串及其長度的變量，就可以完成了。 從代碼結構來看，第一步需要兩層的循環去查找共同出現的字符，這就是 O(nm)。一旦找到了共同出現的字符之后，還需要再繼續查找共同出現的字符串，這也就是又嵌套了一層循環。可見最終的時間復雜度是 O(nmm)，即 O(nm2)。代碼如下： ``` public void s2() { String a = "123456"; String b = "13452439"; String maxSubStr = ""; int max_len = 0; for (int i = 0; i < a.length(); i++) { for (int j = 0; j < b.length(); j++){ if (a.charAt(i) == b.charAt(j)){ for (int m=i, n=j; m<a.length()&&n<b.length(); m++,n++) { if (a.charAt(m) != b.charAt(n)){ break; } if (max_len < m-i+1){ max_len = m-i+1; ? ? ? ? ? ? ? ? maxSubStr = a.substring(i, m+1); } } } } } System.out.println(maxSubStr); } ``` #### 總結 這節課我們介紹了字符串匹配算法，它在平時代碼編寫中都比較常用。 字符串的邏輯結構和線性表極為相似，區別僅在于串的數據對象約束為字符集。但是，字符串的基本操作和線性表有很大差別： * 在線性表的基本操作中，大多以“單個元素”作為操作對象； * 在字符串的基本操作中，通常以“串的整體”作為操作對象； * 字符串的增刪操作和數組很像，復雜度也與之一樣。但字符串的查找操作就復雜多了，它是參加面試、筆試常常被考察的內容。 #### 練習題 最后我們給出一道練習題。給定一個字符串，逐個翻轉字符串中的每個單詞。例如，輸入: "the sky is blue"，輸出: "blue is sky the"。