你好，歡迎進入第 16 課時的學習。在前面課時中，我們已經學習了解決代碼問題的方法論。宏觀上，它可以分為以下 4 個步驟： 1. 復雜度分析。估算問題中復雜度的上限和下限。 2. 定位問題。根據問題類型，確定采用何種算法思維。 3. 數據操作分析。根據增、刪、查和數據順序關系去選擇合適的數據結構，利用空間換取時間。 4. 編碼實現。 這套方法論的框架，是解決絕大多數代碼問題的基本步驟。本課時，我們將在一些更開放的題目中進行演練，繼續訓練你的算法思維。 #### 算法思維訓練題 * [ ] 例題 1：斐波那契數列 斐波那契數列是：0，1，1，2，3，5，8，13，21，34，55，89，144……。你會發現，這個數列中元素的性質是，某個數等于它前面兩個數的和；也就是 a[n+2] = a[n+1] + a[n]。至于起始兩個元素，則分別為 0 和 1。在這個數列中的數字，就被稱為斐波那契數。 【題目】寫一個函數，輸入 x，輸出斐波那契數列中第 x 位的元素。例如，輸入 4，輸出 2；輸入 9，輸出 21。要求：需要用遞歸的方式來實現。 【解析】 在本課時開頭，我們復習了解決代碼問題的方法論，下面我們按照解題步驟進行詳細分析。 * 首先我們還是先做好復雜度的分析 題目中要求要用遞歸的方式來實現，而遞歸的次數與 x 的具體數值有非常強的關系。因此，此時的時間復雜度應該是關于輸入變量 x 的數值大小的函數。 * 至于問題定位 因為題目中已經明確了要采用遞歸去解決。所以也不用再去做額外的分析和判斷了。 那么，如何使用遞歸呢？我們需要依賴斐波那契數列的重要性質“某個數等于它前面兩個數的和”。也就是說，要求出某個位置 x 的數字，需要先求出 x-1 的位置是多少和 x-2 的位置是多少。遞歸同時還需要終止條件，對應于斐波那契數列的性質，就是起始兩個元素，分別為 0 和 1。 * 數據操作方面 斐波那契數列需要對數字進行求和。而且所有的計算，都是依賴最原始的 0 和 1 進行。因此，這道題是不需要設計什么復雜的數據結構的。 * 最后，實現代碼 我們圍繞遞歸的性質進行開發，去試著寫出遞歸體和終止條件。代碼如下： ``` public static void main(String[] args) { int x = 20; System.out.println(fun(x)); } private static int fun(int n) { if (n == 1) { return 0; } if (n == 2) { return 1; } return fun(n - 1) + fun(n - 2); } ``` 下面，我們來對代碼進行解讀。 主函數中，第 1 行到第 4 行，定義輸入變量 x，并調用 fun(x) 去計算第 x 位的斐波那契數列元素。 在 fun() 函數內部，采用了遞歸去完成計算。遞歸分為遞歸體和終止條件： * 遞歸體是第 13 行。即當輸入變量 n 比 2 大的時候，遞歸地調用 fun() 函數，并傳入 n-1 和 n-2，即 return fun(n - 1) + fun(n - 2)； * 終止條件則是在第 7 行到第 12 行，分別定義了當 n 為 1 或 2 的時候，直接返回 0 或 1。 * [ ] 例題2：判斷一個數組中是否存在某個數 【題目】給定一個經過任意位數的旋轉后的排序數組，判斷某個數是否在里面。 例如，對于一個給定數組 {4, 5, 6, 7, 0, 1, 2}，它是將一個有序數組的前三位旋轉地放在了數組末尾。假設輸入的 target 等于 0，則輸出答案是 4，即 0 所在的位置下標是 4。如果輸入 3，則返回 -1。 【解析】 這道題目依舊是按照解決代碼問題的方法論的步驟進行分析。 * 先做復雜度分析 這個問題就是判斷某個數字是否在數組中，因此，復雜度極限就是全部遍歷地去查找，也就是 O(n) 的復雜度。 * 接著，進入定位問題的環節中 * 這個問題有很多關鍵字，因此能夠讓你立馬鎖定問題。例如，判斷某個數是否在數組里面，這就是一個查找問題。 * 然后，我們來做數據操作分析 原數組是經過某些處理的排序數組，也就是說原數組是有序的。有序和查找，你就會很快地想到，這個問題極有可能用二分查找的方式去解決，時間復雜度是 O(logn)，相比上面 O(n) 的基線也是有顯著的提高。 在利用二分查找時，更多的是判斷，基本沒有數據的增刪操作，因此不需要太多地定義復雜的數據結構。 分析到這里，解決方案已經非常明朗了，就是采用二分查找的方法，在 O(logn) 的時間復雜度下去解決這個問題。二分查找可以通過遞歸來實現。而每次遞歸的關鍵點在于，根據切分的點（最中間的那個數字），確定是向左走還是向右走。這也是這個例題中唯一的難點了。 試想一下，在一個旋轉后的有序數組中，利用中間元素作為切分點得到的兩個子數組有什么樣的性質。經過枚舉不難發現，這兩個子數組中，一定存在一個數組是有序的。也可能出現一個極端情況，二者都是有序的。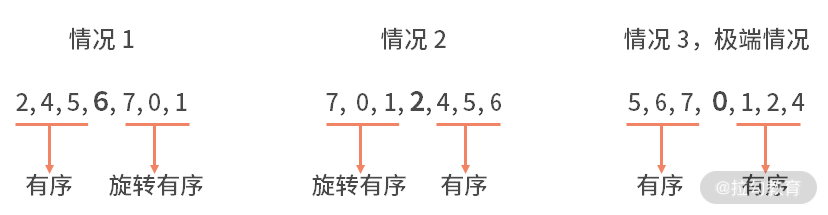如下圖所示：  對于有序的一邊，我們是很容易判斷目標值，是否在這個區間內的。如果在其中，也說明了目標值不在另一邊的旋轉有序組里；反之亦然。 當我們知道了目標值在左右哪邊之后，就可以遞歸地調用旋轉有序的二分查找了。之所以可以遞歸調用，是因為，對于旋轉有序組，這個問題和原始問題完全一致，可以調用。對于有序組，它是旋轉有序的特殊情況（即旋轉 0 位），也一定是可以通過遞歸的方法去實現查找的。直到不斷二分后，搜索空間只有 1 位數字，直接判斷是否找到即可。 * 最后，實現代碼 我們給出這個例子的實現代碼，如下： ``` public static void main(String[] args) { int[] arr = { 4, 5, 6, 7, 0, 1, 2 }; int target = 7; System.out.println(bs(arr, target, 0, arr.length-1)); } private static int bs(int[] arr, int target, int begin, int end) { if (begin == end) { if (target == arr[begin]){ return begin; } else{ return -1; } } int middle = (begin + end)/2; if (target == arr[middle]) { return middle; } if (arr[begin] <= arr[middle-1]){ if (arr[begin] <= target && target <= arr[middle-1]) { return bs(arr,target, begin,middle-1); } else { return bs(arr,target, middle+1,end); } } else { if (arr[middle+1] <= target && target <= arr[end]) { return bs(arr,target, middle+1,end); } else { return bs(arr,target, begin,middle-1); } } } ``` 我們對代碼進行解讀： 主函數中，第 2 到 4 行。定義數組和 target，并且執行二分查找。二分查找包括兩部分，其一是二分策略，其二是終止條件。 二分策略在代碼的 16～33 行： * 16 行計算分裂點的索引值。17 到 19 行，進行目標值與分裂點的判斷。 如果相等，則查找到結果并返回； 如果不等就要繼續二分。 * 在二分的過程中，第 20 行進行了左右子數組哪邊是有序的判斷。 如果左邊有序，則進入到 21 到 25 行； 如果右邊有序，則進入到 28 到 32 行。 * 假設左邊有序，則還需要判斷 target 是否在有序區間內，這是在第 21 行。 如果在，則繼續遞歸的調用 bs(arr,target, begin,middle-1)； 如果不在有序部分，則說明 target 在另一邊的旋轉有序中，則調用 bs(arr,target, middle+1,end)。 下面的邏輯與此類似，不再贅述。 經過了層層二分，最終 begin 和 end 變成了相等的兩個變量，則進入到終止條件，即 8 到 15 行。 在這里，需要判斷最后剩下的 1 個元素是否與 target 相等： * 如果相等則返回索引值； * 如果不等則返回 -1。 #### 例題3：求解最大公共子串 【題目】輸入兩個字符串，用動態規劃的方法，求解出最大公共子串。 例如，輸入 a = "13452439"， b = "123456"。由于字符串"345"同時在 a 和 b 中出現，且是同時出現在 a 和 b 中的最長的子串。因此輸出"345"。 【解析】這里已經定義了問題，就是尋找最大公共子串。同時也定義了方法，就是要用動態規劃的方法。那么我們也不需要做太多的分析，只要依賴動態規劃的步驟完成就可以了。 首先，我們回顧一下先前學過的最短路徑問題。在最短路徑問題中，我們是定義了起點和終點后，再去尋找二者之間的最短路徑。 而現在的最大公共子串問題是，所有相鄰的字符距離都是 1，在不確定起點和終點時，我們需要去尋找起點和終點之間最遠的距離。 如果要基于已有的知識來探索陌生問題，那就需要根據每個可能的公共子串起點，去尋找與之對應的最遠終點。這樣就能得到全部的子串。隨后再從中找到最大的那個子串。 別忘了，動態規劃的基本方法是：分階段、找狀態、做決策、狀態轉移方程、定目標、尋找終止條件。下面我們來具體分析一下動態規劃的步驟： * 對于一個可能的起點，它后面的每個字符都是一個階段。 * 狀態就是當前尋找到的相匹配的字符。 * 決策就是當前找到的字符是否相等（相等則進入到公共子串中）。 * 狀態轉移方程可以寫作 sk+1 = uk(sk)。可以理解為，如果 sk = "123"是公共子串，且在 a 字符串和 b 字符串中，"123"后面的字符相等，假設為"4"，則決策要進入到公共子串中，sk+1 = "1234"。 * 目標自然就是公共子串最長。 * 終止條件就是決策到了不相等的結果。 這段分析對于初學者來說會非常難懂，接下來我們給一個實現的流程來輔助你理解。 我們在最短路徑問題中，曾重點提到的一個難點是，對于輸入的圖，采用什么樣的數據結構予以保存。最終我們選擇了二維數組。 在這個例子中也可以采用二維數組。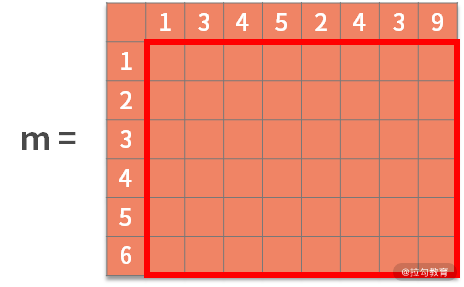每一行或每一列就對應了輸入字符串 a 和 b 的每個字符，即 6 x 8 的二維數組（矩陣）為：  接著，每個可能的起點字符，都應該同時出現在字符串 a 和 b 中，例如"1"就是一個可能的起點。如果以"1"作為起點，那么它后面的字符就是階段，顯然下個階段就是 a[1] = 3 和 b[1] = 2。而此時的狀態就是當前的公共子串，即 "1"。 決策的結果是，下一個階段是否進入到公共子串中。很顯然 a[1] 不等于 b[1]，因此決策的結果是不進入。這也同時命中了終止條件。如果以"3"起點，則因為它之后的 a[2] 等于 b[3]，則決策結果是進入到公共子串。 因此狀態轉移方程 sk+1 = uk(sk)，含義是在"3"的狀態下決策"4"進入子串，結果得到"34"。我們的目標是尋找最大的公共子串，因此可以用從 1 開始的數字定義距離（子串的長度）。具體步驟如下： 對于每個可能的起點，距離都是 1 （不可能的起點置為 0，圖中忽略未寫）。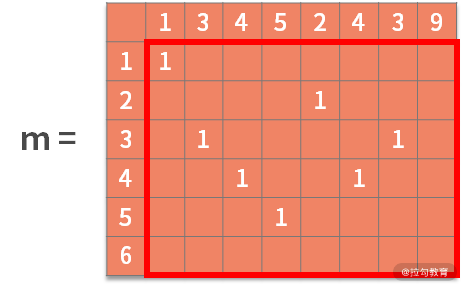則有：  接著利用狀態轉移方程，去尋找最優子結構。也就是，如果 b[i] = a[j]，則 m[i,j] = m[i-1,j-1] + 1。含義為，如果決策結果是相等，則狀態增加一個新的字符，進行更新。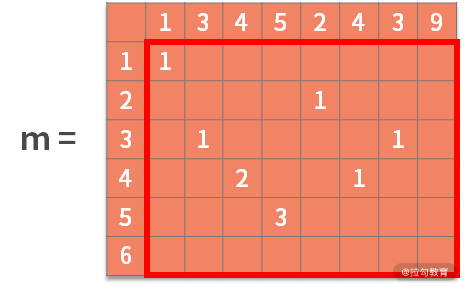可以得到：  最終，檢索這個矩陣，得到的最大數字就是最大公共子串的長度。根據其所在的位置，就能從 a 或 b 中找到最大公共子串。 代碼如下： ``` public static void main(String[] args) { String a = "13452439"; String b = "123456"; getCommenStr(a, b); } public static void getCommenStr(String a, String b) { char[] c1 = a.toCharArray(); char[] c2 = b.toCharArray(); int[][] m = new int[c2.length+1][c1.length+1]; for (int i = 1; i <= c2.length; i++) { for (int j = 1; j <= c1.length; j++) { if (c2[i - 1] == c1[j - 1]) m[i][j] = m[i - 1][j - 1] + 1; } } int max = 0; int index = 0; for (int i = 0; i <= c2.length; i++) { for (int j = 0; j <= c1.length; j++) { if (m[i][j] > max) { max = m[i][j]; index = i; } } } String s = ""; for (int i = index - max; i < index; i++) s += b.charAt(i); System.out.println(s); } ``` 下面我們對代碼進行解讀： 主函數中定義了字符串 a 和字符串 b，隨后調用動態規劃代碼。 進入 getCommenStr() 函數中之后，首先在第 10 行定義了二維數組。此時二維數組的維數是 7 x 9 的。這主要的原因是，后續會需要用到第一行和第一列的全零向量，作為起始條件。 接著，在第 11～16 行，利用雙重循環去完成狀態轉移的計算。此時就得到了最關鍵的矩陣，如下所示：  隨后的 17～26 行，我們從矩陣 m 中，找到了最大值為 3，在字符串 b 中的索引值為 4（此時 index 為 5，但別忘了我們之前額外定義了一行/一列的全零向量）。 最后，27～30 行，我們根據終點字符串索引值 4 和最大公共子串長度 3，就能找到最大公共子串在 b 中的 2～4 的位置。即 "345"。 #### 總結 這一課時中，我們對例題做了詳細的分析和講解，重點其實是訓練你的算法思維。為了檢驗你的學習成果，我們基于斐波那契數列的例題，再給出一個思考題，題目如下： 如果現在是個線上實時交互的系統。客戶端輸入 x，服務端返回斐波那契數列中的第 x 位。那么，這個問題使用上面的解法是否可行。 這里給你一個小提示，既然我這么問，答案顯然是不可行的。如果不可行，原因是什么呢？我們又該如何解決？注意，題目中給出的是一個實時系統。當用戶提交了 x，如果在幾秒內沒有得到系統響應，用戶就會卸載 App 啦。