在前面課時中，我們學習了分治法的思想，并以二分查找為例介紹了分治的實現邏輯。 我們提到過，分治法的使用必須滿足 4 個條件： 1. 問題的解決難度與數據規模有關； 2. 原問題可被分解； 3. 子問題的解可以合并為原問題的解； 4. 所有的子問題相互獨立。 然而在實際工作中還存在這樣一類問題，它們滿足前 3 個條件，唯獨不滿足第 4 個條件。那么這類問題我們該怎么解決呢？本課時，我們就來學習求解這類問題的動態規劃算法，它是最常用的算法之一。 #### 什么是動態規劃 從數學的視角來看，動態規劃是一種運籌學方法，是在多輪決策過程中的最優方法。 那么，什么是多輪決策呢？其實多輪決策的每一輪都可以看作是一個子問題。從分治法的視角來看，每個子問題必須相互獨立。但在多輪決策中，這個假設顯然不成立。這也是動態規劃方法產生的原因之一。 動態規劃是候選人參加面試的噩夢，也是面試過程中的難點。雖然動態規劃很難，但在實際的工作中，使用頻率并不高，不是所有的崗位都會用到動態規劃。 * [ ] 最短路徑問題 接下來。我們來看一個非常典型的例子，最短路徑問題。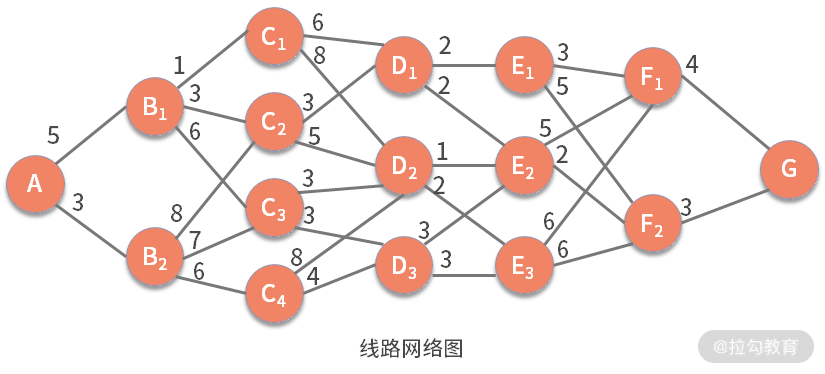如下圖所示：  每個結點是一個位置，每條邊是兩個位置之間的距離。現在需要求解出一條由 A 到 G 的最短距離是多少。 不難發現，我們需要求解的路線是由 A 到 G，這就意味著 A 要先到 B，再到 C，再到 D，再到 E，再到 F。每一輪都需要做不同的決策，而每次的決策又依賴上一輪決策的結果。 例如，做 D2 -> E 的決策時，D2 -> E2 的距離為 1，最短。但這輪的決策，基于的假設是從 D2 出發，這就意味著前面一輪的決策結果是 D2。由此可見，相鄰兩輪的決策結果并不是獨立的。 動態規劃還有一個重要概念叫作狀態。在這個例子中，狀態是個變量，而且受決策動作的影響。例如，第一輪決策的狀態是 S1，可選的值是 A，第二輪決策的狀態是 S2，可選的值就是 B1 和 B2。以此類推。 #### 動態規劃的基本方法 動態規劃問題之所以難，是因為動態規劃的解題方法并沒有那么標準化，它需要你因題而異，仔細分析問題并尋找解決方案。雖然動態規劃問題沒有標準化的解題方法，但它有一些宏觀層面通用的方法論： 下面的 k 表示多輪決策的第 k 輪 1. 分階段，將原問題劃分成幾個子問題。一個子問題就是多輪決策的一個階段，它們可以是不滿足獨立性的。 2. 找狀態，選擇合適的狀態變量 Sk。它需要具備描述多輪決策過程的演變，更像是決策可能的結果。 3. 做決策，確定決策變量 uk。每一輪的決策就是每一輪可能的決策動作，例如 D2 的可能的決策動作是 D2 -> E2 和 D2 -> E3。 4. 狀態轉移方程。這個步驟是動態規劃最重要的核心，即 sk+1= uk(sk)?。 5. 定目標。寫出代表多輪決策目標的指標函數 Vk,n。 6. 尋找終止條件。 了解了方法論、狀態、多輪決策之后，我們再補充一些動態規劃的基本概念。 * 策略，每輪的動作是決策，多輪決策合在一起常常被稱為策略。 * 策略集合，由于每輪的決策動作都是一個變量，這就導致合在一起的策略也是一個變量。我們通常會稱所有可能的策略為策略集合。因此，動態規劃的目標，也可以說是從策略集合中，找到最優的那個策略。 一般而言，具有如下幾個特征的問題，可以采用動態規劃求解： 1. 最優子結構。它的含義是，原問題的最優解所包括的子問題的解也是最優的。例如，某個策略使得 A 到 G 是最優的。假設它途徑了 Fi，那么它從 A 到 Fi 也一定是最優的。 2. 無后效性。某階段的決策，無法影響先前的狀態。可以理解為今天的動作改變不了歷史。 3. 有重疊子問題。也就是，子問題之間不獨立。這個性質是動態規劃區別于分治法的條件。如果原問題不滿足這個特征，也是可以用動態規劃求解的，無非就是殺雞用了宰牛刀。 #### 動態規劃的案例 到這里，動態規劃的概念和方法就講完了。接下來，我們以最短路徑問題再來看看動態規劃的求解方法。在這個問題中，你可以采用最暴力的方法，那就是把所有的可能路徑都遍歷一遍，去看哪個結果的路徑最短的。如果采用動態規劃方法，那么我們按照方法論來執行。 * [ ] 動態規劃的求解方法 具體的解題步驟如下： 1. 分階段 很顯然，從 A 到 G，可以拆分為 A -> B、B -> C、C -> D、D -> E、E -> F、F -> G，6 個階段。 2. 找狀態 第一輪的狀態 S1 = A，第二輪 S2 = {B1,B2}，第三輪 S3 = {C1,C2,C3,C4}，第四輪 S4 = {D1,D2,D3}，第五輪 S5 = {E1,E2,E3}，第六輪 S6 = {F1,F2}，第七輪 S7 = {G}。 3. 做決策 決策變量就是上面圖中的每條邊。我們以第四輪決策 D -> E 為例來看，可以得到 u4(D1)，u4(D2)，u4(D3)。其中 u4(D1) 的可能結果是 E1 和 E2。 4. 寫出狀態轉移方程 在這里，就是 sk+1 = uk(sk)。 5. 定目標 別忘了，我們的目標是總距離最短。我們定義 dk(sk,uk) 是在 sk 時，選擇 uk 動作的距離。例如，d5(E1,F1) = 3。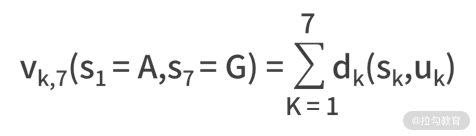那么此時 n = 7，則有，  就是最終要優化的目標。 6. 尋找終止條件 * 很顯然，這里的起止條件分別是，s1 = A 和 s7 = G。 * 接下來，我們把所有的已知條件，凝練為上面的符號之后，只需要借助最優子結構，就可以把問題解決了。最優子結構的含義是，原問題的最優解所包括的子問題的解也是最優的。 * 套用在這個例子的含義就是，如果 A -> ... -> F1 -> G 是全局 A 到 G 最優的路徑，那么此處 A -> ... -> F1 也是 A 到 F1 的最優路徑。 * 因此，此時的優化目標 min Vk,7(s1=A, s7=G)，等價于 min { Vk,6(s1=A, s6=F1)+4， Vk,6(s1=A, s6=F2)+3 }。 * 此時，優化目標的含義為，從 A 到 G 的最短路徑，是 A 到 F1 到 G 的路徑和 A 到 F2 到 G 的路徑中更短的那個。 * 同樣的，對于上面式子中，Vk,6(s1=A,s6=F1) 和 Vk,6(s1=A,s6=F2)，仍然可以遞歸地使用上面的分析方法。 * [ ] 計算過程詳解 好了，為了讓大家清晰地看到結果，我們給出詳細的計算過程。為了書寫簡單，我們把函數 Vk,7(s1=A, s7=G) 精簡為 V7(G)，含義為經過了 6 輪決策后，狀態到達 G 后所使用的距離。我們把圖片復制到這里一份，方便大家不用上下切換。  我們的優化目標為 min Vk,7(s1=A, s7=G)，因此精簡后原問題為，min V7(G)。       因此，最終輸出路徑為 A -> B1 -> C2 -> D1 -> E2 -> F2 -> G，最短距離為 18。 * [ ] 代碼實現過程 接下來，我們嘗試用代碼來實現上面的計算過程。對于輸入的圖，可以采用一個 m x m 的二維數組來保存。在這個二維數組里，m 等于全部的結點數，也就是結點與結點的關系圖。而數組每個元素的數值，定義為結點到結點需要的距離。  在本例中，可以定義輸入矩陣 m（空白處為0），如下圖所示：  代碼如下： ``` public class testpath { public static int minPath1(int[][] matrix) { return process1(matrix, matrix[0].length-1); } // 遞歸 public static int process1(int[][] matrix, int i) { // 到達A退出遞歸 if (i == 0) { return 0; } // 狀態轉移 else{ int distance = 999; for(int j=0; j<i; j++){ if(matrix[j][i]!=0){ int d_tmp = matrix[j][i] + process1(matrix, j); if (d_tmp < distance){ distance = d_tmp; } } } return distance; } } public static void main(String[] args) { int[][] m = {{0,5,3,0,0,0,0,0,0,0,0,0,0,0,0,0},{0,0,0,1,3,6,0,0,0,0,0,0,0,0,0,0},{0,0,0,0,8,7,6,0,0,0,0,0,0,0,0,0},{0,0,0,0,0,0,0,6,8,0,0,0,0,0,0,0},{0,0,0,0,0,0,0,3,5,0,0,0,0,0,0,0},{0,0,0,0,0,0,0,0,3,3,0,0,0,0,0,0},{0,0,0,0,0,0,0,0,8,4,0,0,0,0,0,0},{0,0,0,0,0,0,0,0,0,0,2,2,0,0,0,0},{0,0,0,0,0,0,0,0,0,0,0,1,2,0,0,0},{0,0,0,0,0,0,0,0,0,0,0,3,3,0,0,0},{0,0,0,0,0,0,0,0,0,0,0,0,0,3,5,0},{0,0,0,0,0,0,0,0,0,0,0,0,0,5,2,0},{0,0,0,0,0,0,0,0,0,0,0,0,0,6,6,0},{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,4},{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,3}}; System.out.println(minPath1(m)); } } ``` * [ ] 代碼解讀 下面我們對這段代碼進行解讀： 代碼的 27 行是主函數，在代碼中定義了二維數組 m，對應于輸入的距離圖。m 是 15 x 16 維的，我們忽略了最后一行的全 0（即使輸入也不會影響結果）。 然后調用函數 minPath1。在第 2 到第 4 行，它的內部又調用了 process1(matrix, matrix[0].length-1)。在這里，matrix[0].length-1 的值是 15，表示的含義是 matrix 數組的第 16 列（G）是目的地。 接著進入 process1 函數中。我們知道在動態規劃的過程中，是從后往前不斷地推進結果，這就是狀態轉移的過程。對應代碼中的 13-24 行： * 第 15 行開始循環，j 變量是縱向的循環變量。 * 第 16 行判斷 matrix[j][i] 與 0 的關系，含義為，只有值不為 0 才說明兩個結點之間存在通路。 * 一旦發現某個通路，就需要計算其距離。計算的方式是 17 行的，d_tmp = matrix[j][i] + process1(matrix, j)。 * 當得到了距離之后，還需要找到最短的那個距離，也就是 18 到 20 行的含義。這就是動態規劃最優子結構的體現。 * 一旦 i 減小到了 0，就說明已經到了起點 A。那么 A 到 A 的距離就是 0，直接第 10 行的 return 0 就可以了。 * 經過運行，這段代碼的輸出結果是 18，這與我們手動的推導結果一致。 #### 練習題 在 08 課時中，我們講述“字符串匹配算法的案例”時提到過，最大公共子串也可以使用動態規劃的方法來做。 案例題目如下： 假設有且僅有 1 個最大公共子串。比如，輸入 a =?"13452439"， b =?"123456"。由于字符串?"345"?同時在 a 和 b 中出現，且是同時出現在 a 和 b 中的最長子串。因此輸出?"345"。 我們就把這個問題當作本課時的練習題。答案會在后面的實戰章節中公布。 #### 總結 動態規劃領域有很多經典問題，本課時，我們講述了最短路徑的問題。需要明確的是，動態規劃并不簡單，動態規劃的適用范圍也沒有那么廣。如果你不是專門從事運籌優化領域的工作，對它不了解也很正常。如果在求職過程中，你求職的崗位與運籌優化關系不大，一般而言被考察到動態規劃的可能性也是極低的。