# 五、支持向量機
> 譯者:[@QiaoXie](https://github.com/QiaoXie)
>
> 校對者:[@飛龍](https://github.com/wizardforcel)、[@PeterHo](https://github.com/PeterHo)、[@yanmengk](https://github.com/yanmengk)、[@YuWang](https://github.com/bigeyex)
支持向量機(SVM)是個非常強大并且有多種功能的機器學習模型,能夠做線性或者非線性的分類,回歸,甚至異常值檢測。機器學習領域中最為流行的模型之一,是任何學習機器學習的人必備的工具。SVM 特別適合應用于復雜但中小規模數據集的分類問題。
本章節將闡述支持向量機的核心概念,怎么使用這個強大的模型,以及它是如何工作的。
## 線性支持向量機分類
SVM 的基本思想能夠用一些圖片來解釋得很好,圖 5-1 展示了我們在第4章結尾處介紹的鳶尾花數據集的一部分。這兩個種類能夠被非常清晰,非常容易的用一條直線分開(即線性可分的)。左邊的圖顯示了三種可能的線性分類器的判定邊界。其中用虛線表示的線性模型判定邊界很差,甚至不能正確地劃分類別。另外兩個線性模型在這個數據集表現的很好,但是它們的判定邊界很靠近樣本點,在新的數據上可能不會表現的很好。相比之下,右邊圖中 SVM 分類器的判定邊界實線,不僅分開了兩種類別,而且還盡可能地遠離了最靠近的訓練數據點。你可以認為 SVM 分類器在兩種類別之間保持了一條盡可能寬敞的街道(圖中平行的虛線),其被稱為最大間隔分類。
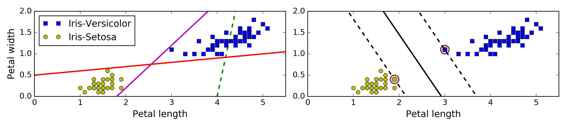
我們注意到添加更多的樣本點在“街道”外并不會影響到判定邊界,因為判定邊界是由位于“街道”邊緣的樣本點確定的,這些樣本點被稱為“支持向量”(圖 5-1 中被圓圈圈起來的點)
> 警告
>
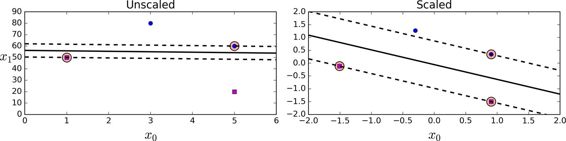
> SVM 對特征縮放比較敏感,可以看到圖 5-2:左邊的圖中,垂直的比例要更大于水平的比例,所以最寬的“街道”接近水平。但對特征縮放后(例如使用Scikit-Learn的StandardScaler),判定邊界看起來要好得多,如右圖。
### 軟間隔分類
如果我們嚴格地規定所有的數據都不在“街道”上,都在正確地兩邊,稱為硬間隔分類,硬間隔分類有兩個問題,第一,只對線性可分的數據起作用,第二,對異常點敏感。圖 5-3 顯示了只有一個異常點的鳶尾花數據集:左邊的圖中很難找到硬間隔,右邊的圖中判定邊界和我們之前在圖 5-1 中沒有異常點的判定邊界非常不一樣,它很難一般化。
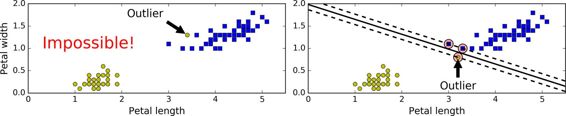
為了避免上述的問題,我們更傾向于使用更加軟性的模型。目的在保持“街道”盡可能大和避免間隔違規(例如:數據點出現在“街道”中央或者甚至在錯誤的一邊)之間找到一個良好的平衡。這就是軟間隔分類。
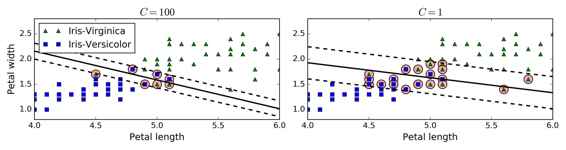
在 Scikit-Learn 庫的 SVM 類,你可以用`C`超參數(懲罰系數)來控制這種平衡:較小的`C`會導致更寬的“街道”,但更多的間隔違規。圖 5-4 顯示了在非線性可分隔的數據集上,兩個軟間隔SVM分類器的判定邊界。左邊圖中,使用了較大的`C`值,導致更少的間隔違規,但是間隔較小。右邊的圖,使用了較小的`C`值,間隔變大了,但是許多數據點出現在了“街道”上。然而,第二個分類器似乎泛化地更好:事實上,在這個訓練數據集上減少了預測錯誤,因為實際上大部分的間隔違規點出現在了判定邊界正確的一側。
> 提示
>
> 如果你的 SVM 模型過擬合,你可以嘗試通過減小超參數`C`去調整。
以下的 Scikit-Learn 代碼加載了內置的鳶尾花(Iris)數據集,縮放特征,并訓練一個線性 SVM 模型(使用`LinearSVC`類,超參數`C=1`,hinge 損失函數)來檢測 Virginica 鳶尾花,生成的模型在圖 5-4 的右圖。
```py
import numpy as np
from sklearn import datasets
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
iris = datasets.load_iris()
X = iris["data"][:, (2, 3)] # petal length, petal width
y = (iris["target"] == 2).astype(np.float64) # Iris-Virginica
svm_clf = Pipeline((
("scaler", StandardScaler()),
("linear_svc", LinearSVC(C=1, loss="hinge")),
))
svm_clf.fit(X, y)
Then, as usual, you can use the model to make predictions:
>>> svm_clf.predict([[5.5, 1.7]])
array([ 1.])
```
> 注
>
> 不同于 Logistic 回歸分類器,SVM 分類器不會輸出每個類別的概率。
作為一種選擇,你可以在 SVC 類,使用`SVC(kernel="linear", C=1)`,但是它比較慢,尤其在較大的訓練集上,所以一般不被推薦。另一個選擇是使用`SGDClassifier`類,即`SGDClassifier(loss="hinge", alpha=1/(m*C))`。它應用了隨機梯度下降(SGD 見第四章)來訓練一個線性 SVM 分類器。盡管它不會和`LinearSVC`一樣快速收斂,但是對于處理那些不適合放在內存的大數據集是非常有用的,或者處理在線分類任務同樣有用。
> 提示
>
> `LinearSVC`要使偏置項規范化,首先你應該集中訓練集減去它的平均數。如果你使用了`StandardScaler`,那么它會自動處理。此外,確保你設置`loss`參數為`hinge `,因為它不是默認值。最后,為了得到更好的效果,你需要將`dual`參數設置為`False`,除非特征數比樣本量多(我們將在本章后面討論二元性)
## 非線性支持向量機分類
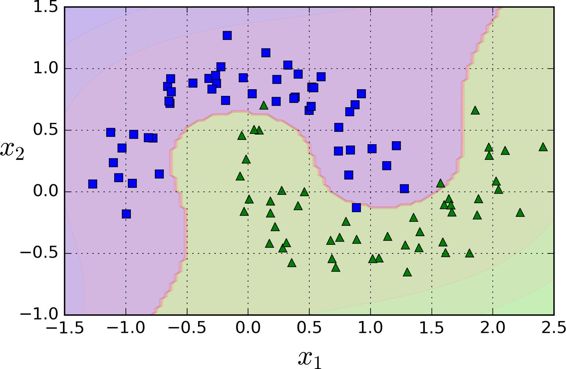
盡管線性 SVM 分類器在許多案例上表現得出乎意料的好,但是很多數據集并不是線性可分的。一種處理非線性數據集方法是增加更多的特征,例如多項式特征(正如你在第4章所做的那樣);在某些情況下可以變成線性可分的數據。在圖 5-5的左圖中,它只有一個特征`x1`的簡單的數據集,正如你看到的,該數據集不是線性可分的。但是如果你增加了第二個特征 `x2=(x1)^2`,產生的 2D 數據集就能很好的線性可分。
為了實施這個想法,通過 Scikit-Learn,你可以創建一個流水線(Pipeline)去包含多項式特征(PolynomialFeatures)變換(在 121 頁的“Polynomial Regression”中討論),然后一個`StandardScaler`和`LinearSVC`。讓我們在衛星數據集(moons datasets)測試一下效果。
```py
from sklearn.datasets import make_moons
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
polynomial_svm_clf = Pipeline((
("poly_features", PolynomialFeatures(degree=3)),
("scaler", StandardScaler()),
("svm_clf", LinearSVC(C=10, loss="hinge"))
))
polynomial_svm_clf.fit(X, y)
```
### 多項式核
添加多項式特征很容易實現,不僅僅在 SVM,在各種機器學習算法都有不錯的表現,但是低次數的多項式不能處理非常復雜的數據集,而高次數的多項式卻產生了大量的特征,會使模型變得慢。
幸運的是,當你使用 SVM 時,你可以運用一個被稱為“核技巧”(kernel trick)的神奇數學技巧。它可以取得就像你添加了許多多項式,甚至有高次數的多項式,一樣好的結果。所以不會大量特征導致的組合爆炸,因為你并沒有增加任何特征。這個技巧可以用 SVC 類來實現。讓我們在衛星數據集測試一下效果。
```py
from sklearn.svm import SVC
poly_kernel_svm_clf = Pipeline((
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="poly", degree=3, coef0=1, C=5))
))
poly_kernel_svm_clf.fit(X, y)
```
這段代碼用3階的多項式核訓練了一個 SVM 分類器,即圖 5-7 的左圖。右圖是使用了10階的多項式核 SVM 分類器。很明顯,如果你的模型過擬合,你可以減小多項式核的階數。相反的,如果是欠擬合,你可以嘗試增大它。超參數`coef0`控制了高階多項式與低階多項式對模型的影響。

通用的方法是用網格搜索(grid search 見第 2 章)去找到最優超參數。首先進行非常粗略的網格搜索一般會很快,然后在找到的最佳值進行更細的網格搜索。對每個超參數的作用有一個很好的理解可以幫助你在正確的超參數空間找到合適的值。
### 增加相似特征
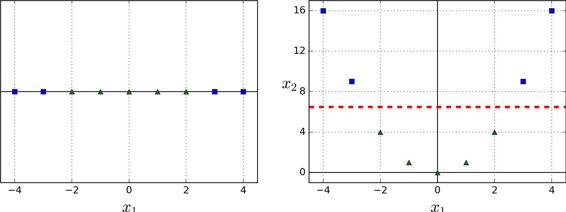
另一種解決非線性問題的方法是使用相似函數(similarity funtion)計算每個樣本與特定地標(landmark)的相似度。例如,讓我們來看看前面討論過的一維數據集,并在`x1=-2`和`x1=1`之間增加兩個地標(圖 5-8 左圖)。接下來,我們定義一個相似函數,即高斯徑向基函數(Gaussian Radial Basis Function,RBF),設置`γ = 0.3`(見公式 5-1)
公式 5-1 RBF

它是個從 0 到 1 的鐘型函數,值為 0 的離地標很遠,值為 1 的在地標上。現在我們準備計算新特征。例如,我們看一下樣本`x1=-1`:它距離第一個地標距離是 1,距離第二個地標是 2。因此它的新特征為`x2=exp(-0.3 × (1^2))≈0.74`和`x3=exp(-0.3 × (2^2))≈0.30`。圖 5-8 右邊的圖顯示了特征轉換后的數據集(刪除了原始特征),正如你看到的,它現在是線性可分了。
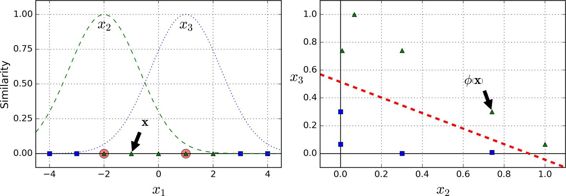
你可能想知道如何選擇地標。最簡單的方法是在數據集中的每一個樣本的位置創建地標。這將產生更多的維度從而增加了轉換后數據集是線性可分的可能性。但缺點是,`m`個樣本,`n`個特征的訓練集被轉換成了`m`個實例,`m`個特征的訓練集(假設你刪除了原始特征)。這樣一來,如果你的訓練集非常大,你最終會得到同樣大的特征。
### 高斯 RBF 核
就像多項式特征法一樣,相似特征法對各種機器學習算法同樣也有不錯的表現。但是在所有額外特征上的計算成本可能很高,特別是在大規模的訓練集上。然而,“核” 技巧再一次顯現了它在 SVM 上的神奇之處:高斯核讓你可以獲得同樣好的結果成為可能,就像你在相似特征法添加了許多相似特征一樣,但事實上,你并不需要在RBF添加它們。我們使用 SVC 類的高斯 RBF 核來檢驗一下。
```py
rbf_kernel_svm_clf = Pipeline((
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="rbf", gamma=5, C=0.001))
))
rbf_kernel_svm_clf.fit(X, y)
```
這個模型在圖 5-9 的左下角表示。其他的圖顯示了用不同的超參數`gamma (γ)`和`C`訓練的模型。增大`γ`使鐘型曲線更窄(圖 5-8 左圖),導致每個樣本的影響范圍變得更小:即判定邊界最終變得更不規則,在單個樣本周圍環繞。相反的,較小的`γ`值使鐘型曲線更寬,樣本有更大的影響范圍,判定邊界最終則更加平滑。所以γ是可調整的超參數:如果你的模型過擬合,你應該減小`γ`值,若欠擬合,則增大`γ`(與超參數`C`相似)。
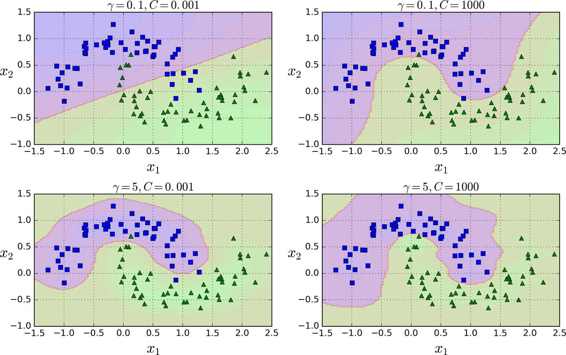
還有其他的核函數,但很少使用。例如,一些核函數是專門用于特定的數據結構。在對文本文檔或者 DNA 序列進行分類時,有時會使用字符串核(String kernels)(例如,使用 SSK 核(string subsequence kernel)或者基于編輯距離(Levenshtein distance)的核函數)。
> 提示
>
> 這么多可供選擇的核函數,你如何決定使用哪一個?一般來說,你應該先嘗試線性核函數(記住`LinearSVC`比`SVC(kernel="linear")`要快得多),尤其是當訓練集很大或者有大量的特征的情況下。如果訓練集不太大,你也可以嘗試高斯徑向基核(Gaussian RBF Kernel),它在大多數情況下都很有效。如果你有空閑的時間和計算能力,你還可以使用交叉驗證和網格搜索來試驗其他的核函數,特別是有專門用于你的訓練集數據結構的核函數。
### 計算復雜性
`LinearSVC`類基于`liblinear`庫,它實現了線性 SVM 的優化算法。它并不支持核技巧,但是它樣本和特征的數量幾乎是線性的:訓練時間復雜度大約為`O(m × n)`。
如果你要非常高的精度,這個算法需要花費更多時間。這是由容差值超參數`?`(在 Scikit-learn 稱為`tol`)控制的。大多數分類任務中,使用默認容差值的效果是已經可以滿足一般要求。
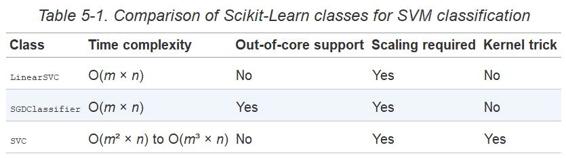
SVC 類基于`libsvm`庫,它實現了支持核技巧的算法。訓練時間復雜度通常介`于O(m^2 × n)`和`O(m^3 × n)`之間。不幸的是,這意味著當訓練樣本變大時,它將變得極其慢(例如,成千上萬個樣本)。這個算法對于復雜但小型或中等數量的數據集表現是完美的。然而,它能對特征數量很好的縮放,尤其對稀疏特征來說(sparse features)(即每個樣本都有一些非零特征)。在這個情況下,算法對每個樣本的非零特征的平均數量進行大概的縮放。表 5-1 對 Scikit-learn 的 SVM 分類模型進行比較。
## SVM 回歸
正如我們之前提到的,SVM 算法應用廣泛:不僅僅支持線性和非線性的分類任務,還支持線性和非線性的回歸任務。技巧在于逆轉我們的目標:限制間隔違規的情況下,不是試圖在兩個類別之間找到盡可能大的“街道”(即間隔)。SVM 回歸任務是限制間隔違規情況下,盡量放置更多的樣本在“街道”上。“街道”的寬度由超參數`?`控制。圖 5-10 顯示了在一些隨機生成的線性數據上,兩個線性 SVM 回歸模型的訓練情況。一個有較大的間隔(`?=1.5`),另一個間隔較小(`?=0.5`)。
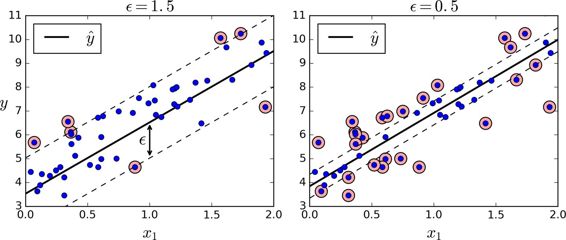
添加更多的數據樣本在間隔之內并不會影響模型的預測,因此,這個模型認為是不敏感的(?-insensitive)。
你可以使用 Scikit-Learn 的`LinearSVR`類去實現線性 SVM 回歸。下面的代碼產生的模型在圖 5-10 左圖(訓練數據需要被中心化和標準化)
```py
from sklearn.svm import LinearSVR
svm_reg = LinearSVR(epsilon=1.5)
svm_reg.fit(X, y)
```
處理非線性回歸任務,你可以使用核化的 SVM 模型。比如,圖 5-11 顯示了在隨機二次方的訓練集,使用二次方多項式核函數的 SVM 回歸。左圖是較小的正則化(即更大的`C`值),右圖則是更大的正則化(即小的`C`值)
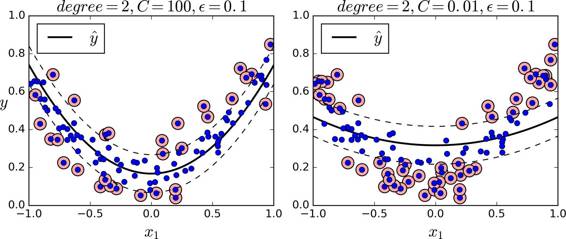
下面的代碼的模型在圖 5-11,其使用了 Scikit-Learn 的`SVR`類(支持核技巧)。在回歸任務上,`SVR`類和`SVC`類是一樣的,并且`LinearSVR`是和`LinearSVC`等價。`LinearSVR`類和訓練集的大小成線性(就像`LinearSVC`類),當訓練集變大,`SVR`會變的很慢(就像`SVC`類)
```py
from sklearn.svm import SVR
svm_poly_reg = SVR(kernel="poly", degree=2, C=100, epsilon=0.1)
svm_poly_reg.fit(X, y)
```
> 注
>
> SVM 也可以用來做異常值檢測,詳情見 Scikit-Learn 文檔
## 背后機制
這個章節從線性 SVM 分類器開始,將解釋 SVM 是如何做預測的并且算法是如何工作的。如果你是剛接觸機器學習,你可以跳過這個章節,直接進入本章末尾的練習。等到你想深入了解 SVM,再回頭研究這部分內容。
首先,關于符號的約定:在第 4 章,我們將所有模型參數放在一個矢量`θ`里,包括偏置項`θ0`,`θ1`到`θn`的輸入特征權重,和增加一個偏差輸入`x0 = 1`到所有樣本。在本章中,我們將使用一個不同的符號約定,在處理 SVM 上,這更方便,也更常見:偏置項被命名為`b`,特征權重向量被稱為`w`,在輸入特征向量中不再添加偏置特征。
### 決策函數和預測
線性 SVM 分類器通過簡單地計算決策函數  來預測新樣本的類別:如果結果是正的,預測類別`?`是正類,為 1,否則他就是負類,為 0。見公式 5-2

圖 5-12 顯示了和圖 5-4 右邊圖模型相對應的決策函數:因為這個數據集有兩個特征(花瓣的寬度和花瓣的長度),所以是個二維的平面。決策邊界是決策函數等于 0 的點的集合,圖中兩個平面的交叉處,即一條直線(圖中的實線)
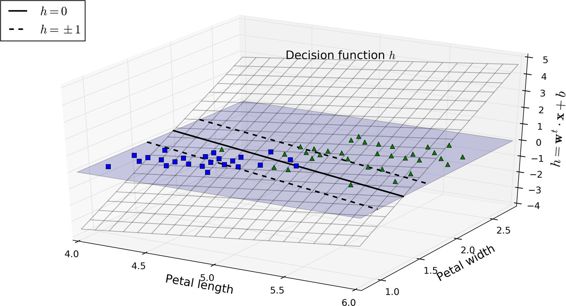
虛線表示的是那些決策函數等于 1 或 -1 的點:它們平行,且到決策邊界的距離相等,形成一個間隔。訓練線性 SVM 分類器意味著找到`w`值和`b`值使得這一個間隔盡可能大,同時避免間隔違規(硬間隔)或限制它們(軟間隔)
### 訓練目標
看下決策函數的斜率:它等于權重向量的范數 。如果我們把這個斜率除于 2,決策函數等于 ±1 的點將會離決策邊界原來的兩倍大。換句話,即斜率除于 2,那么間隔將增加兩倍。在圖 5-13 中,2D 形式比較容易可視化。權重向量`w`越小,間隔越大。
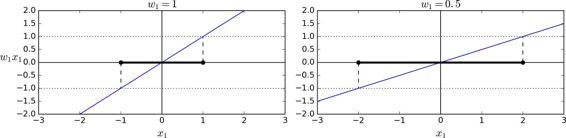
所以我們的目標是最小化 ,從而獲得大的間隔。然而,如果我們想要避免間隔違規(硬間隔),對于正的訓練樣本,我們需要決策函數大于 1,對于負訓練樣本,小于 -1。若我們對負樣本(即 )定義 ,對正樣本(即 )定義 ,那么我們可以對所有的樣本表示為 。
因此,我們可以將硬間隔線性 SVM 分類器表示為公式 5-3 中的約束優化問題

> 注
>
>  等于 ,我們最小化 ,而不是最小化 。這會給我們相同的結果(因為最小化`w`值和`b`值,也是最小化該值一半的平方),但是  有很好又簡單的導數(只有`w`), 在`w=0`處是不可微的。優化算法在可微函數表現得更好。
為了獲得軟間隔的目標,我們需要對每個樣本應用一個松弛變量(slack variable)。 表示了第`i`個樣本允許違規間隔的程度。我們現在有兩個不一致的目標:一個是使松弛變量盡可能的小,從而減小間隔違規,另一個是使`1/2 w·w`盡量小,從而增大間隔。這時`C`超參數發揮作用:它允許我們在兩個目標之間權衡。我們得到了公式 5-4 的約束優化問題。

### 二次規劃
硬間隔和軟間隔都是線性約束的凸二次規劃優化問題。這些問題被稱之為二次規劃(QP)問題。現在有許多解決方案可以使用各種技術來處理 QP 問題,但這超出了本書的范圍。一般問題的公式在公式 5-5 給出。

注意到表達式`Ap ≤ b`實際上定義了  約束: , 是個包含了`A`的第`i`行元素的向量,是`b`的第`i`個元素。
可以很容易地看到,如果你用以下的方式設置 QP 的參數,你將獲得硬間隔線性 SVM 分類器的目標:
+ ,`n`表示特征的數量(+1 是偏置項)
+ ,`m`表示訓練樣本數量
+ `H`是  單位矩陣,除了左上角為 0(忽略偏置項)
+ `f = 0`,一個全為 0 的  維向量
+ ,一個全為 1 的  維向量
+ , 等于  帶一個額外的偏置特征 !
所以訓練硬間隔線性 SVM 分類器的一種方式是使用現有的 QP 解決方案,即上述的參數。由此產生的向量`p`將包含偏置項  和特征權重 。同樣的,你可以使用 QP 解決方案來解決軟間隔問題(見本章最后的練習)
然而,使用核技巧我們將會看到一個不同的約束優化問題。
### 對偶問題
給出一個約束優化問題,即原始問題(primal problem),它可能表示不同但是和另一個問題緊密相連,稱為對偶問題(Dual Problem)。對偶問題的解通常是對原始問題的解給出一個下界約束,但在某些條件下,它們可以獲得相同解。幸運的是,SVM 問題恰好滿足這些條件,所以你可以選擇解決原始問題或者對偶問題,兩者將會有相同解。公式 5-6 表示了線性 SVM 的對偶形式(如果你對怎么從原始問題獲得對偶問題感興趣,可以看下附錄 C)

一旦你找到最小化公式的向量`α`(使用 QP 解決方案),你可以通過使用公式 5-7 的方法計算`w`和`b`,從而使原始問題最小化。

當訓練樣本的數量比特征數量小的時候,對偶問題比原始問題要快得多。更重要的是,它讓核技巧成為可能,而原始問題則不然。那么這個核技巧是怎么樣的呢?
### 核化支持向量機
假設你想把一個 2 次多項式變換應用到二維空間的訓練集(例如衛星數據集),然后在變換后的訓練集上訓練一個線性SVM分類器。公式 5-8 顯示了你想應用的 2 次多項式映射函數`?`。

注意到轉換后的向量是 3 維的而不是 2 維。如果我們應用這個 2 次多項式映射,然后計算轉換后向量的點積(見公式 5-9),讓我們看下兩個 2 維向量`a`和`b`會發生什么。

轉換后向量的點積等于原始向量點積的平方:
關鍵點是:如果你應用轉換`?`到所有訓練樣本,那么對偶問題(見公式 5-6)將會包含點積 。但如果`?`像在公式 5-8 定義的 2 次多項式轉換,那么你可以將這個轉換后的向量點積替換成 。所以實際上你根本不需要對訓練樣本進行轉換:僅僅需要在公式 5-6 中,將點積替換成它點積的平方。結果將會和你經過麻煩的訓練集轉換并擬合出線性 SVM 算法得出的結果一樣,但是這個技巧使得整個過程在計算上面更有效率。這就是核技巧的精髓。
函數  被稱為二次多項式核(polynomial kernel)。在機器學習,核函數是一個能計算點積的函數,并只基于原始向量`a`和`b`,不需要計算(甚至知道)轉換`?`。公式 5-10 列舉了一些最常用的核函數。

> Mercer 定理
>
> 根據 Mercer 定理,如果函數`K(a, b)`滿足一些 Mercer 條件的數學條件(`K`函數在參數內必須是連續,對稱,即`K(a, b)=K(b, a)`,等),那么存在函數`?`,將`a`和`b`映射到另一個空間(可能有更高的維度),有 。所以你可以用`K`作為核函數,即使你不知道`?`是什么。使用高斯核(Gaussian RBF kernel)情況下,它實際是將每個訓練樣本映射到無限維空間,所以你不需要知道是怎么執行映射的也是一件好事。
>
> 注意一些常用核函數(例如 Sigmoid 核函數)并不滿足所有的 Mercer 條件,然而在實踐中通常表現得很好。
我們還有一個問題要解決。公式 5-7 展示了線性 SVM 分類器如何從對偶解到原始解,如果你應用了核技巧那么得到的公式會包含 。事實上,`w`必須和  有同樣的維度,可能是巨大的維度或者無限的維度,所以你很難計算它。但怎么在不知道`w`的情況下做出預測?好消息是你可以將公式 5-7 的`w`代入到新的樣本  的決策函數中,你會得到一個在輸入向量之間只有點積的方程式。這時,核技巧將派上用場,見公式 5-11

注意到支持向量才滿足`α(i)≠0`,做出預測只涉及計算為支持向量部分的輸入樣本  的點積,而不是全部的訓練樣本。當然,你同樣也需要使用同樣的技巧來計算偏置項`b`,見公式 5-12

如果你開始感到頭痛,這很正常:因為這是核技巧一個不幸的副作用
### 在線支持向量機
在結束這一章之前,我們快速地了解一下在線 SVM 分類器(回想一下,在線學習意味著增量地學習,不斷有新實例)。對于線性SVM分類器,一種方式是使用梯度下降(例如使用`SGDClassifire`)最小化代價函數,如從原始問題推導出的公式 5-13。不幸的是,它比基于 QP 方式收斂慢得多。

代價函數第一個和會使模型有一個小的權重向量`w`,從而獲得一個更大的間隔。第二個和計算所有間隔違規的總數。如果樣本位于“街道”上和正確的一邊,或它與“街道”正確一邊的距離成比例,則間隔違規等于 0。最小化保證了模型的間隔違規盡可能小并且少。
> Hinge 損失
>
> 函數`max(0, 1–t)`被稱為 Hinge 損失函數(如下)。當`t≥1`時,Hinge 值為 0。如果`t<1`,它的導數(斜率)為 -1,若`t>1`,則等于0。在`t=1`處,它是不可微的,但就像套索回歸(Lasso Regression)(參見 130 頁套索回歸)一樣,你仍然可以在`t=0`時使用梯度下降法(即 -1 到 0 之間任何值)
>
> 
我們也可以實現在線核化的 SVM。例如使用“增量和遞減 SVM 學習”或者“在線和主動的快速核分類器”。但是,這些都是用 Matlab 和 C++ 實現的。對于大規模的非線性問題,你可能需要考慮使用神經網絡(見第二部分)
## 練習
1. 支持向量機背后的基本思想是什么
2. 什么是支持向量
3. 當使用 SVM 時,為什么標準化輸入很重要?
4. 分類一個樣本時,SVM 分類器能夠輸出一個置信值嗎?概率呢?
5. 在一個有數百萬訓練樣本和數百特征的訓練集上,你是否應該使用 SVM 原始形式或對偶形式來訓練一個模型?
6. 假設你用 RBF 核來訓練一個 SVM 分類器,如果對訓練集欠擬合:你應該增大或者減小`γ`嗎?調整參數`C`呢?
7. 使用現有的 QP 解決方案,你應該怎么樣設置 QP 參數(`H`,`f`,`A`,和`b`)去解決一個軟間隔線性 SVM 分類器問題?
8. 在一個線性可分的數據集訓練一個`LinearSVC`,并在同一個數據集上訓練一個`SVC`和`SGDClassifier`,看它們是否產生了大致相同效果的模型。
9. 在 MNIST 數據集上訓練一個 SVM 分類器。因為 SVM 分類器是二元的分類,你需要使用一對多(one-versus-all)來對 10 個數字進行分類。你可能需要使用小的驗證集來調整超參數,以加快進程。最后你能達到多少準確度?
0. 在加利福尼亞住宅(California housing)數據集上訓練一個 SVM 回歸模型
這些練習的答案在附錄 A。
