八、降維 · Sklearn 與 TensorFlow 機器學習實用指南

# 八、降維 > 譯者：[@loveSnowBest](https://github.com/zehuichen123) > > 校對者：[@飛龍](https://github.com/wizardforcel)、[@PeterHo](https://github.com/PeterHo)、[@yanmengk](https://github.com/yanmengk)、[@XinQiu](https://github.com/xinqiu)、[@Lisanaaa](https://github.com/Lisanaaa) 很多機器學習的問題都會涉及到有著幾千甚至數百萬維的特征的訓練實例。這不僅讓訓練過程變得非常緩慢，同時還很難找到一個很好的解，我們接下來就會遇到這種情況。這種問題通常被稱為維數災難（curse of dimentionality）。幸運的是，在現實生活中我們經常可以極大的降低特征維度，將一個十分棘手的問題轉變成一個可以較為容易解決的問題。例如，對于 MNIST 圖片集（第 3 章中提到）：圖片四周邊緣部分的像素幾乎總是白的，因此你完全可以將這些像素從你的訓練集中扔掉而不會丟失太多信息。圖 7-6 向我們證實了這些像素的確對我們的分類任務是完全不重要的。同時，兩個相鄰的像素往往是高度相關的：如果你想要將他們合并成一個像素（比如取這兩個像素點的平均值）你并不會丟失很多信息。 > 警告：降維肯定會丟失一些信息（這就好比將一個圖片壓縮成 JPEG 的格式會降低圖像的質量），因此即使這種方法可以加快訓練的速度，同時也會讓你的系統表現的稍微差一點。降維會讓你的工作流水線更復雜因而更難維護。所有你應該先嘗試使用原始的數據來訓練，如果訓練速度太慢的話再考慮使用降維。在某些情況下，降低訓練集數據的維度可能會篩選掉一些噪音和不必要的細節，這可能會讓你的結果比降維之前更好（這種情況通常不會發生；它只會加快你訓練的速度）。降維除了可以加快訓練速度外，在數據可視化方面（或者 DataViz）也十分有用。降低特征維度到 2（或者 3）維從而可以在圖中畫出一個高維度的訓練集，讓我們可以通過視覺直觀的發現一些非常重要的信息，比如聚類。在這一章里，我們將會討論維數災難問題并且了解在高維空間的數據。然后，我們將會展示兩種主要的降維方法：投影（projection）和流形學習（Manifold Learning），同時我們還會介紹三種流行的降維技術：主成分分析（PCA），核主成分分析（Kernel PCA）和局部線性嵌入（LLE）。 ## 維數災難我們已經習慣生活在一個三維的世界里，以至于當我們嘗試想象更高維的空間時，我們的直覺不管用了。即使是一個基本的 4D 超正方體也很難在我們的腦中想象出來（見圖 8-1），更不用說一個 200 維的橢球彎曲在一個 1000 維的空間里了。 ![](https://img.kancloud.cn/fc/12/fc12a78ebadf3023a377165066ac2db7_566x187.gif) 圖 8-1 點，線，方形，立方體和超正方體（0D 到 4D 超正方體）這表明很多物體在高維空間表現的十分不同。比如，如果你在一個正方形單元中隨機取一個點（一個`1×1`的正方形），那么隨機選的點離所有邊界大于 0.001（靠近中間位置）的概率為 0.4%（`1 - 0.998^2`）（換句話說，一個隨機產生的點不大可能嚴格落在某一個維度上。但是在一個 1,0000 維的單位超正方體（一個`1×1×...×1`的立方體，有 10,000 個 1），這種可能性超過了 99.999999%。在高維超正方體中，大多數點都分布在邊界處。還有一個更麻煩的區別：如果你在一個平方單位中隨機選取兩個點，那么這兩個點之間的距離平均約為 0.52。如果您在單位 3D 立方體中選取兩個隨機點，平均距離將大致為 0.66。但是，在一個 1,000,000 維超立方體中隨機抽取兩點呢？那么，平均距離，信不信由你，大概為 408.25（大致 ![\sqrt{1,000,000/6}](https://img.kancloud.cn/e9/ab/e9ab1ec0f818efa45f81a8f9e84b8463_113x23.gif)）！這非常違反直覺：當它們都位于同一單元超立方體內時，兩點是怎么距離這么遠的？這一事實意味著高維數據集有很大風險分布的非常稀疏：大多數訓練實例可能彼此遠離。當然，這也意味著一個新實例可能遠離任何訓練實例，這使得預測的可靠性遠低于我們處理較低維度數據的預測，因為它們將基于更大的推測（extrapolations）。簡而言之，訓練集的維度越高，過擬合的風險就越大。理論上來說，維數爆炸的一個解決方案是增加訓練集的大小從而達到擁有足夠密度的訓練集。不幸的是，在實踐中，達到給定密度所需的訓練實例的數量隨著維度的數量呈指數增長。如果只有 100 個特征（比 MNIST 問題要少得多）并且假設它們均勻分布在所有維度上，那么如果想要各個臨近的訓練實例之間的距離在 0.1 以內，您需要比宇宙中的原子還要多的訓練實例。 ## 降維的主要方法在我們深入研究具體的降維算法之前，我們來看看降低維度的兩種主要方法：投影和流形學習。 ### 投影（Projection）在大多數現實生活的問題中，訓練實例并不是在所有維度上均勻分布的。許多特征幾乎是常數，而其他特征則高度相關（如前面討論的 MNIST）。結果，所有訓練實例實際上位于（或接近）高維空間的低維子空間內。這聽起來有些抽象，所以我們不妨來看一個例子。在圖 8-2 中，您可以看到由圓圈表示的 3D 數據集。 ![](https://img.kancloud.cn/97/fb/97fb380bd0afae4efba190b2a16277f8_566x363.jpeg) 圖 8-2 一個分布接近于2D子空間的3D數據集注意到所有訓練實例的分布都貼近一個平面：這是高維（3D）空間的較低維（2D）子空間。現在，如果我們將每個訓練實例垂直投影到這個子空間上（就像將短線連接到平面的點所表示的那樣），我們就可以得到如圖8-3所示的新2D數據集。鐺鐺鐺！我們剛剛將數據集的維度從 3D 降低到了 2D。請注意，坐標軸對應于新的特征`z1`和`z2`（平面上投影的坐標）。 ![](https://img.kancloud.cn/ea/a2/eaa2ec881dcad3bf06ab6697283450ea_566x484.gif) 圖 8-3 一個經過投影后的新的 2D 數據集但是，投影并不總是降維的最佳方法。在很多情況下，子空間可能會扭曲和轉動，比如圖 8-4 所示的著名瑞士滾動玩具數據集。 ![](https://img.kancloud.cn/fa/b9/fab99d2b989381f12c1f1d45e35a8017_566x436.jpeg) 圖 8-4 瑞士滾動數玩具數據集簡單地將數據集投射到一個平面上（例如，直接丟棄`x3`）會將瑞士卷的不同層疊在一起，如圖 8-5 左側所示。但是，你真正想要的是展開瑞士卷所獲取到的類似圖 8-5 右側的 2D 數據集。 ![](https://img.kancloud.cn/f0/fb/f0fbf9672c67c09c0df5e352061461de_566x195.jpeg) 圖 8-5 投射到平面的壓縮（左）vs 展開瑞士卷（右） ### 流形學習瑞士卷一個是二維流形的例子。簡而言之，二維流形是一種二維形狀，它可以在更高維空間中彎曲或扭曲。更一般地，一個`d`維流形是類似于`d`維超平面的`n`維空間（其中`d < n`）的一部分。在我們瑞士卷這個例子中，`d = 2`，`n = 3`：它有些像 2D 平面，但是它實際上是在第三維中卷曲。許多降維算法通過對訓練實例所在的流形進行建模從而達到降維目的；這叫做流形學習。它依賴于流形猜想（manifold assumption），也被稱為流形假設（manifold hypothesis），它認為大多數現實世界的高維數據集大都靠近一個更低維的流形。這種假設經常在實踐中被證實。讓我們再回到 MNIST 數據集：所有手寫數字圖像都有一些相似之處。它們由連線組成，邊界是白色的，大多是在圖片中中間的，等等。如果你隨機生成圖像，只有一小部分看起來像手寫數字。換句話說，如果您嘗試創建數字圖像，那么您的自由度遠低于您生成任何隨便一個圖像時的自由度。這些約束往往會將數據集壓縮到較低維流形中。流形假設通常包含著另一個隱含的假設：你現在的手上的工作（例如分類或回歸）如果在流形的較低維空間中表示，那么它們會變得更簡單。例如，在圖 8-6 的第一行中，瑞士卷被分為兩類：在三維空間中（圖左上），分類邊界會相當復雜，但在二維展開的流形空間中（圖右上），分類邊界是一條簡單的直線。但是，這個假設并不總是成立。例如，在圖 8-6 的最下面一行，決策邊界位于`x1 = 5`（圖左下）。這個決策邊界在原始三維空間（一個垂直平面）看起來非常簡單，但在展開的流形中卻變得更復雜了（四個獨立線段的集合）（圖右下）。簡而言之，如果在訓練模型之前降低訓練集的維數，那訓練速度肯定會加快，但并不總是會得出更好的訓練效果；這一切都取決于數據集。希望你現在對于維數爆炸以及降維算法如何解決這個問題有了一定的理解，特別是對流形假設提出的內容。本章的其余部分將介紹一些最流行的降維算法。 ![](https://img.kancloud.cn/1f/22/1f22ebdbc497e8d1695eaede475200bc_566x454.jpeg) 圖 8-6 決策邊界并不總是會在低維空間中變的簡單 ## 主成分分析（PCA）主成分分析（Principal Component Analysis）是目前為止最流行的降維算法。首先它找到接近數據集分布的超平面，然后將所有的數據都投影到這個超平面上。 ### 保留（最大）方差在將訓練集投影到較低維超平面之前，您首先需要選擇正確的超平面。例如圖 8-7 左側是一個簡單的二維數據集，以及三個不同的軸（即一維超平面）。圖右邊是將數據集投影到每個軸上的結果。正如你所看到的，投影到實線上保留了最大方差，而在點線上的投影只保留了非常小的方差，投影到虛線上保留的方差則處于上述兩者之間。 ![](https://img.kancloud.cn/78/84/788480a8abe61e97562a5940e619a0a5_566x273.jpeg) 圖 8-7 選擇投射到哪一個子空間選擇保持最大方差的軸看起來是合理的，因為它很可能比其他投影損失更少的信息。證明這種選擇的另一種方法是，選擇這個軸使得將原始數據集投影到該軸上的均方距離最小。這是就 PCA 背后的思想，相當簡單。 ### 主成分（Principle Componets） PCA 尋找訓練集中可獲得最大方差的軸。在圖 8-7 中，它是一條實線。它還發現了一個與第一個軸正交的第二個軸，選擇它可以獲得最大的殘差。在這個 2D 例子中，沒有選擇：就只有這條點線。但如果在一個更高維的數據集中，PCA 也可以找到與前兩個軸正交的第三個軸，以及與數據集中維數相同的第四個軸，第五個軸等。定義第`i`個軸的單位矢量被稱為第`i`個主成分（PC）。在圖 8-7 中，第一個 PC 是`c1`，第二個 PC 是`c2`。在圖 8-2 中，前兩個 PC 用平面中的正交箭頭表示，第三個 PC 與上述 PC 形成的平面正交（指向上或下）。 > 概述：主成分的方向不穩定：如果您稍微打亂一下訓練集并再次運行 PCA，則某些新 PC 可能會指向與原始 PC 方向相反。但是，它們通常仍位于同一軸線上。在某些情況下，一對 PC 甚至可能會旋轉或交換，但它們定義的平面通常保持不變。那么如何找到訓練集的主成分呢？幸運的是，有一種稱為奇異值分解（SVD）的標準矩陣分解技術，可以將訓練集矩陣`X`分解為三個矩陣`U·Σ·V^T`的點積，其中`V^T`包含我們想要的所有主成分，如公式 8-1 所示。公式 8-1 主成分矩陣 ![](https://img.kancloud.cn/2b/a7/2ba7455133cd27b1d8bb667d280d0563_469x204.gif) 下面的 Python 代碼使用了 Numpy 提供的`svd()`函數獲得訓練集的所有主成分，然后提取前兩個 PC: ```Python X_centered=X-X.mean(axis=0) U,s,V=np.linalg.svd(X_centered) c1=V.T[:,0] c2=V.T[:,1] ``` > 警告：PCA 假定數據集以原點為中心。正如我們將看到的，Scikit-Learn 的`PCA`類負責為您的數據集中心化處理。但是，如果您自己實現 PCA（如前面的示例所示），或者如果您使用其他庫，不要忘記首先要先對數據做中心化處理。 ### 投影到`d`維空間一旦確定了所有的主成分，你就可以通過將數據集投影到由前`d`個主成分構成的超平面上，從而將數據集的維數降至`d`維。選擇這個超平面可以確保投影將保留盡可能多的方差。例如，在圖 8-2 中，3D 數據集被投影到由前兩個主成分定義的 2D 平面，保留了大部分數據集的方差。因此，2D 投影看起來非常像原始 3D 數據集。為了將訓練集投影到超平面上，可以簡單地通過計算訓練集矩陣`X`和`Wd`的點積，`Wd`定義為包含前`d`個主成分的矩陣（即由`V^T`的前`d`列組成的矩陣），如公式 8-2 所示。公式 8-2 將訓練集投影到`d`維空間 ![X_{d-proj} = X \cdot W_d](https://img.kancloud.cn/8e/78/8e78e2aa750d276fd8a25640f17e696c_135x18.gif) 下面的 Python 代碼將訓練集投影到由前兩個主成分定義的超平面上： ```Python W2=V.T[:,:2] X2D=X_centered.dot(W2) ``` 好了你已經知道這個東西了！你現在已經知道如何給任何一個數據集降維而又能盡可能的保留原數據集的方差了。 ### 使用 Scikit-Learn Scikit-Learn 的 PCA 類使用 SVD 分解來實現，就像我們之前做的那樣。以下代碼應用 PCA 將數據集的維度降至兩維（請注意，它會自動處理數據的中心化）： ```Python from sklearn.decomposition import PCA pca=PCA(n_components=2) X2D=pca.fit_transform(X) ``` 將 PCA 轉化器應用于數據集后，可以使用`components_`訪問每一個主成分（注意，它返回以 PC 作為水平向量的矩陣，因此，如果我們想要獲得第一個主成分則可以寫成`pca.components_.T[:,0]`）。 ### 方差解釋率（Explained Variance Ratio）另一個非常有用的信息是每個主成分的方差解釋率，可通過`explained_variance_ratio_`變量獲得。它表示位于每個主成分軸上的數據集方差的比例。例如，讓我們看一下圖 8-2 中表示的三維數據集前兩個分量的方差解釋率： ``` >>> print(pca.explained_variance_ratio_) array([0.84248607, 0.14631839]) ``` 這表明，84.2% 的數據集方差位于第一軸，14.6% 的方差位于第二軸。第三軸的這一比例不到1.2％，因此可以認為它可能沒有包含什么信息。 ### 選擇正確的維度通常我們傾向于選擇加起來到方差解釋率能夠達到足夠占比（例如 95%）的維度的數量，而不是任意選擇要降低到的維度數量。當然，除非您正在為數據可視化而降低維度 -- 在這種情況下，您通常希望將維度降低到 2 或 3。下面的代碼在不降維的情況下進行 PCA，然后計算出保留訓練集方差 95% 所需的最小維數： ```Python pca=PCA() pac.fit(X) cumsum=np.cumsum(pca.explained_variance_ratio_) d=np.argmax(cumsum>=0.95)+1 ``` 你可以設置`n_components = d`并再次運行 PCA。但是，有一個更好的選擇：不指定你想要保留的主成分個數，而是將`n_components`設置為 0.0 到 1.0 之間的浮點數，表明您希望保留的方差比率： ```Python pca=PCA(n_components=0.95) X_reduced=pca.fit_transform(X) ``` 另一種選擇是畫出方差解釋率關于維數的函數（簡單地繪制`cumsum`；參見圖 8-8）。曲線中通常會有一個肘部，方差解釋率停止快速增長。您可以將其視為數據集的真正的維度。在這種情況下，您可以看到將維度降低到大約100個維度不會失去太多的可解釋方差。 ![](https://img.kancloud.cn/42/1c/421ca62d8dc9d18147349091718d82ce_566x360.jpeg) 圖 8-8 可解釋方差關于維數的函數 ### PCA 壓縮顯然，在降維之后，訓練集占用的空間要少得多。例如，嘗試將 PCA 應用于 MNIST 數據集，同時保留 95% 的方差。你應該發現每個實例只有 150 多個特征，而不是原來的 784 個特征。因此，盡管大部分方差都保留下來，但數據集現在還不到其原始大小的 20%！這是一個合理的壓縮比率，您可以看到這可以如何極大地加快分類算法（如 SVM 分類器）的速度。通過應用 PCA 投影的逆變換，也可以將縮小的數據集解壓縮回 784 維。當然這并不會返回給你最原始的數據，因為投影丟失了一些信息（在5％的方差內），但它可能非常接近原始數據。原始數據和重構數據之間的均方距離（壓縮然后解壓縮）被稱為重構誤差（reconstruction error）。例如，下面的代碼將 MNIST 數據集壓縮到 154 維，然后使用`inverse_transform()`方法將其解壓縮回 784 維。圖 8-9 顯示了原始訓練集（左側）的幾位數字在壓縮并解壓縮后（右側）的對應數字。您可以看到有輕微的圖像質量降低，但數字仍然大部分完好無損。 ```Python pca=PCA(n_components=154) X_mnist_reduced=pca.fit_transform(X_mnist) X_mnist_recovered=pca.inverse_transform(X_mnist_reduced) ``` ![](https://img.kancloud.cn/78/1b/781b356099ed4b8d4928790128b35296_566x284.gif) 圖 8-9 MNIST 保留 95 方差的壓縮逆變換的公式如公式 8-3 所示公式 8-3 PCA逆變換，回退到原來的數據維度 ![X_{recovered} = X_{d-proj} \cdot W_d^T](https://img.kancloud.cn/fa/45/fa45c8cbb6af089646d2e4bbabb18cfe_195x22.gif) ### 增量 PCA（Incremental PCA）先前 PCA 實現的一個問題是它需要在內存中處理整個訓練集以便 SVD 算法運行。幸運的是，我們已經開發了增量 PCA（IPCA）算法：您可以將訓練集分批，并一次只對一個批量使用 IPCA 算法。這對大型訓練集非常有用，并且可以在線應用 PCA（即在新實例到達時即時運行）。下面的代碼將 MNIST 數據集分成 100 個小批量（使用 NumPy 的`array_split()`函數），并將它們提供給 Scikit-Learn 的`IncrementalPCA`類，以將 MNIST 數據集的維度降低到 154 維（就像以前一樣）。請注意，您必須對每個最小批次調用`partial_fit()`方法，而不是對整個訓練集使用`fit()`方法： ```Python from sklearn.decomposition import IncrementalPCA n_batches=100 inc_pca=IncrementalPCA(n_components=154) for X_batch in np.array_spplit(X_mnist,n_batches): inc_pca.partial_fit(X_batch) X_mnist_reduced=inc_pca.transform(X_mnist) ``` 或者，您可以使用 NumPy 的`memmap`類，它允許您操作存儲在磁盤上二進制文件中的大型數組，就好像它完全在內存中；該類僅在需要時加載內存中所需的數據。由于增量 PCA 類在任何時間內僅使用數組的一小部分，因此內存使用量仍受到控制。這可以調用通常的`fit()`方法，如下面的代碼所示： ```Python X_mm=np.memmap(filename,dtype='float32',mode='readonly',shape=(m,n)) batch_size=m//n_batches inc_pca=IncrementalPCA(n_components=154,batch_size=batch_size) inc_pca.fit(X_mm) ``` ### 隨機 PCA（Randomized PCA） Scikit-Learn 提供了另一種執行 PCA 的選擇，稱為隨機 PCA。這是一種隨機算法，可以快速找到前d個主成分的近似值。它的計算復雜度是`O(m × d^2) + O(d^3)`，而不是`O(m × n^2) + O(n^3)`，所以當`d`遠小于`n`時，它比之前的算法快得多。 ```Python rnd_pca=PCA(n_components=154,svd_solver='randomized') X_reduced=rnd_pca.fit_transform(X_mnist) ``` ## 核 PCA（Kernel PCA）在第 5 章中，我們討論了核技巧，一種將實例隱式映射到非常高維空間（稱為特征空間）的數學技術，讓支持向量機可以應用于非線性分類和回歸。回想一下，高維特征空間中的線性決策邊界對應于原始空間中的復雜非線性決策邊界。事實證明，同樣的技巧可以應用于 PCA，從而可以執行復雜的非線性投影來降低維度。這就是所謂的核 PCA（kPCA）。它通常能夠很好地保留投影后的簇，有時甚至可以展開分布近似于扭曲流形的數據集。例如，下面的代碼使用 Scikit-Learn 的`KernelPCA`類來執行帶有 RBF 核的 kPCA（有關 RBF 核和其他核的更多詳細信息，請參閱第 5 章）： ```Python from sklearn.decomposition import KernelPCA rbf_pca=KernelPCA(n_components=2,kernel='rbf',gamma=0.04) X_reduced=rbf_pca.fit_transform(X) ``` 圖 8-10 展示了使用線性核（等同于簡單的使用 PCA 類），RBF 核，sigmoid 核（Logistic）將瑞士卷降到 2 維。 ![](https://img.kancloud.cn/e5/22/e5227b851eb3948fc57d3dd623012052_566x194.jpeg) 圖 8-10 使用不同核的 kPCA 將瑞士卷降到 2 維 ### 選擇一種核并調整超參數由于 kPCA 是無監督學習算法，因此沒有明顯的性能指標可以幫助您選擇最佳的核方法和超參數值。但是，降維通常是監督學習任務（例如分類）的準備步驟，因此您可以簡單地使用網格搜索來選擇可以讓該任務達到最佳表現的核方法和超參數。例如，下面的代碼創建了一個兩步的流水線，首先使用 kPCA 將維度降至兩維，然后應用 Logistic 回歸進行分類。然后它使用`Grid SearchCV`為 kPCA 找到最佳的核和`gamma`值，以便在最后獲得最佳的分類準確性： ```Python from sklearn.model_selection import GridSearchCV from sklearn.linear_model import LogisticRegression from sklearn.pipeline import Pipeline clf = Pipeline([ ("kpca", KernelPCA(n_components=2)), ("log_reg", LogisticRegression()) ]) param_grid = [{ "kpca__gamma": np.linspace(0.03, 0.05, 10), "kpca__kernel": ["rbf", "sigmoid"] }] grid_search = GridSearchCV(clf, param_grid, cv=3) grid_search.fit(X, y) ``` 你可以通過調用`best_params_`變量來查看使模型效果最好的核和超參數： ```Python >>> print(grid_search.best_params_) {'kpca__gamma': 0.043333333333333335, 'kpca__kernel': 'rbf'} ``` 另一種完全為非監督的方法，是選擇產生最低重建誤差的核和超參數。但是，重建并不像線性 PCA 那樣容易。這里是原因：圖 8-11 顯示了原始瑞士卷 3D 數據集（左上角），并且使用 RBF 核應用 kPCA 后生成的二維數據集（右上角）。由于核技巧，這在數學上等同于使用特征映射`φ`將訓練集映射到無限維特征空間（右下），然后使用線性 PCA 將變換的訓練集投影到 2D。請注意，如果我們可以在縮減空間中對給定實例實現反向線性 PCA 步驟，則重構點將位于特征空間中，而不是位于原始空間中（例如，如圖中由`x`表示的那樣）。由于特征空間是無限維的，我們不能找出重建點，因此我們無法計算真實的重建誤差。幸運的是，可以在原始空間中找到一個貼近重建點的點。這被稱為重建前圖像（reconstruction pre-image）。一旦你有這個前圖像，你就可以測量其與原始實例的平方距離。然后，您可以選擇最小化重建前圖像錯誤的核和超參數。 ![](https://img.kancloud.cn/69/07/6907ce453bda0243509695f6434aba01_566x456.jpeg) 圖 8-11 核 PCA 和重建前圖像誤差您可能想知道如何進行這種重建。一種解決方案是訓練一個監督回歸模型，將預計實例作為訓練集，并將原始實例作為訓練目標。如果您設置了`fit_inverse_transform = True`，Scikit-Learn 將自動執行此操作，代碼如下所示： ```Python rbf_pca = KernelPCA(n_components = 2, kernel="rbf", gamma=0.0433,fit_inverse_transform=True) X_reduced = rbf_pca.fit_transform(X) X_preimage = rbf_pca.inverse_transform(X_reduced) ``` > 概述：默認條件下，`fit_inverse_transform = False`并且`KernelPCA`沒有`inverse_tranfrom()`方法。這種方法僅僅當`fit_inverse_transform = True`的情況下才會創建。你可以計算重建前圖像誤差： ```Python >>> from sklearn.metrics import mean_squared_error >>> mean_squared_error(X, X_preimage) 32.786308795766132 ``` 現在你可以使用交叉驗證的方格搜索來尋找可以最小化重建前圖像誤差的核方法和超參數。 ### LLE 局部線性嵌入（Locally Linear Embedding）是另一種非常有效的非線性降維（NLDR）方法。這是一種流形學習技術，不依賴于像以前算法那樣的投影。簡而言之，LLE 首先測量每個訓練實例與其最近鄰（c.n.）之間的線性關系，然后尋找能最好地保留這些局部關系的訓練集的低維表示（稍后會詳細介紹）。這使得它特別擅長展開扭曲的流形，尤其是在沒有太多噪音的情況下。例如，以下代碼使用 Scikit-Learn 的`LocallyLinearEmbedding`類來展開瑞士卷。得到的二維數據集如圖 8-12 所示。正如您所看到的，瑞士卷被完全展開，實例之間的距離保存得很好。但是，距離不能在較大范圍內保留的很好：展開的瑞士卷的左側被擠壓，而右側的部分被拉長。盡管如此，LLE 在對流形建模方面做得非常好。 ```Python from sklearn.manifold import LocallyLinearEmbedding lle=LocallyLinearEmbedding(n_components=2,n_neighbors=10) X_reduced=lle.fit_transform(X) ``` ![](https://img.kancloud.cn/48/7d/487da60a012e719c12071e4f2e5cc622_566x377.jpeg) 圖 8-12 使用 LLE 展開瑞士卷這是LLE的工作原理：首先，對于每個訓練實例 ![x^{(i)}](https://img.kancloud.cn/96/a5/96a50da5f7374d8d6617c053fb22558a_23x18.gif)，該算法識別其最近的`k`個鄰居（在前面的代碼中`k = 10`中），然后嘗試將 ![x^{(i)}](https://img.kancloud.cn/96/a5/96a50da5f7374d8d6617c053fb22558a_23x18.gif) 重構為這些鄰居的線性函數。更具體地，找到權重 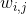![w_{i,j}](https://img.kancloud.cn/78/88/788821b30557ab3dadfc4f65ce202ff2_27x14.gif) 從而使 ![x^{(i)}](https://img.kancloud.cn/96/a5/96a50da5f7374d8d6617c053fb22558a_23x18.gif) 和 ![\sum_{j=1}^{m}w_{i,j} x^{(j)}](https://img.kancloud.cn/11/ae/11ae246daaa09d1e3609a5873f5d1413_81x53.gif) 之間的平方距離盡可能的小，假設如果 ![x^{(j)}](https://img.kancloud.cn/4e/2b/4e2b3dea12f381b3f5cb61078eade436_25x18.gif) 不是 ![x^{(i)}](https://img.kancloud.cn/96/a5/96a50da5f7374d8d6617c053fb22558a_23x18.gif) 的`k`個最近鄰時 ![w_{i,j}=0](https://img.kancloud.cn/d4/da/d4dad64138a0114ca1ede5d7355cfda8_61x18.gif)。因此，LLE 的第一步是方程 8-4 中描述的約束優化問題，其中`W`是包含所有權重 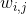![w_{i,j}](https://img.kancloud.cn/78/88/788821b30557ab3dadfc4f65ce202ff2_27x14.gif) 的權重矩陣。第二個約束簡單地對每個訓練實例 ![x^{(i)}](https://img.kancloud.cn/96/a5/96a50da5f7374d8d6617c053fb22558a_23x18.gif) 的權重進行歸一化。公式 8-2 LLE 第一步：對局部關系進行線性建模 ![](https://img.kancloud.cn/5e/f5/5ef53356c0a5551381e10c1f9317571b_299x71.gif) 在這步之后，權重矩陣 ![\widehat{W}](https://img.kancloud.cn/65/b7/65b7e1f5148a2a76cf37af1291004be1_20x20.gif)（包含權重 ![\hat{w_{i,j}}](https://img.kancloud.cn/8d/03/8d03602ee01080ba3df6f31e16d962ec_27x19.gif) 對訓練實例的線形關系進行編碼。現在第二步是將訓練實例投影到一個`d`維空間（`d < n`）中去，同時盡可能的保留這些局部關系。如果 ![z^{(i)}](https://img.kancloud.cn/b0/3a/b03a342ae421912725b82aeb31c73d02_22x18.gif) 是 ![x^{(i)}](https://img.kancloud.cn/96/a5/96a50da5f7374d8d6617c053fb22558a_23x18.gif) 在這個`d`維空間的圖像，那么我們想要 ![z^{(i)}](https://img.kancloud.cn/b0/3a/b03a342ae421912725b82aeb31c73d02_22x18.gif) 和 ![\sum_{j=1}^{m}\hat{w_{i,j}}\ z^{(j)}](https://img.kancloud.cn/1c/13/1c135d1c39be1e5d31e6936a33d74597_86x53.gif) 之間的平方距離盡可能的小。這個想法讓我們提出了公式8-5中的非限制性優化問題。它看起來與第一步非常相似，但我們要做的不是保持實例固定并找到最佳權重，而是恰相反：保持權重不變，并在低維空間中找到實例圖像的最佳位置。請注意，`Z`是包含所有 ![z^{(i)}](https://img.kancloud.cn/b0/3a/b03a342ae421912725b82aeb31c73d02_22x18.gif) 的矩陣。公式 8-3 LLE 第二步：保持關系的同時進行降維 ![](https://img.kancloud.cn/b6/bc/b6bc406934ccd60295fe29ebd125aebc_501x85.gif) Scikit-Learn 的 LLE 實現具有如下的計算復雜度：查找`k`個最近鄰為`O(m log(m) n log(k))`，優化權重為`O(m n k^3)`，建立低維表示為`O(d m^2)`。不幸的是，最后一項`m^2`使得這個算法在處理大數據集的時候表現較差。 ## 其他降維方法還有很多其他的降維方法，Scikit-Learn 支持其中的好幾種。這里是其中最流行的： - 多維縮放（MDS）在嘗試保持實例之間距離的同時降低了維度（參見圖 8-13） - Isomap 通過將每個實例連接到最近的鄰居來創建圖形，然后在嘗試保持實例之間的測地距離時降低維度。 - t-分布隨機鄰域嵌入（t-Distributed Stochastic Neighbor Embedding，t-SNE）可以用于降低維??度，同時試圖保持相似的實例臨近并將不相似的實例分開。它主要用于可視化，尤其是用于可視化高維空間中的實例（例如，可以將MNIST圖像降維到 2D 可視化）。 - 線性判別分析（Linear Discriminant Analysis，LDA）實際上是一種分類算法，但在訓練過程中，它會學習類之間最有區別的軸，然后使用這些軸來定義用于投影數據的超平面。LDA 的好處是投影會盡可能地保持各個類之間距離，所以在運行另一種分類算法（如 SVM 分類器）之前，LDA 是很好的降維技術。 ![](https://img.kancloud.cn/9e/ef/9eefd882978c6427e0d0ea317c2d9536_566x195.jpeg) 圖 8-13 使用不同的技術將瑞士卷降維至 2D ## 練習 1. 減少數據集維度的主要動機是什么？主要缺點是什么？ 2. 什么是維度爆炸？ 3. 一旦對某數據集降維，我們可能恢復它嗎？如果可以，怎樣做才能恢復？如果不可以，為什么？ 4. PCA 可以用于降低一個高度非線性對數據集嗎？ 5. 假設你對一個 1000 維的數據集應用 PCA，同時設置方差解釋率為 95%，你的最終數據集將會有多少維？ 6. 在什么情況下你會使用普通的 PCA，增量 PCA，隨機 PCA 和核 PCA？ 7. 你該如何評價你的降維算法在你數據集上的表現？ 8. 將兩個不同的降維算法串聯使用有意義嗎？ 9. 加載 MNIST 數據集（在第 3 章中介紹），并將其分成一個訓練集和一個測試集（將前 60,000 個實例用于訓練，其余 10,000 個用于測試）。在數據集上訓練一個隨機森林分類器，并記錄了花費多長時間，然后在測試集上評估模型。接下來，使用 PCA 降低數據集的維度，設置方差解釋率為 95%。在降維后的數據集上訓練一個新的隨機森林分類器，并查看需要多長時間。訓練速度更快？接下來評估測試集上的分類器：它與以前的分類器比較起來如何？ 10. 使用 t-SNE 將 MNIST 數據集縮減到二維，并使用 Matplotlib 繪制結果圖。您可以使用 10 種不同顏色的散點圖來表示每個圖像的目標類別。或者，您可以在每個實例的位置寫入彩色數字，甚至可以繪制數字圖像本身的降維版本（如果繪制所有數字，則可視化可能會過于混亂，因此您應該繪制隨機樣本或只在周圍沒有其他實例被繪制的情況下繪制）。你將會得到一個分隔良好的的可視化數字集群。嘗試使用其他降維算法，如 PCA，LLE 或 MDS，并比較可視化結果。練習答案請見附錄 A。