# 十六、強化學習 > 譯者：[@friedhelm739](https://github.com/friedhelm739) > > 校對者：[@飛龍](https://github.com/wizardforcel)、[@rickllyxu](https://github.com/rickllyxu) 強化學習（RL）如今是機器學習的一大令人激動的領域，當然之前也是。自從 1950 年被發明出來后，它在這些年產生了一些有趣的應用，尤其是在游戲（例如 TD-Gammon，一個西洋雙陸棋程序）和及其控制領域，但是從未弄出什么大新聞。直到 2013 年一個革命性的發展：來自英國的研究者發起了一項 Deepmind 項目，這個項目可以學習去玩任何從頭開始的 Atari 游戲，甚至多數比人類玩的還要好，它僅使用像素作為輸入而沒有使用游戲規則的任何先驗知識。這是一系列令人驚嘆的壯舉中的第一個，并在 2016 年 3 月以他們的系統阿爾法狗戰勝了世界圍棋冠軍李世石而告終。從未有程序能勉強打敗這個游戲的大師，更不用說世界冠軍了。今天，RL 的整個領域正在沸騰著新的想法，其都具有廣泛的應用范圍。DeepMind 在 2014 被谷歌以超過 5 億美元收購。 那么他們是怎么做到的呢？事后看來，原理似乎相當簡單：他們將深度學習運用到強化學習領域，結果卻超越了他們最瘋狂的設想。在本章中，我們將首先解釋強化學習是什么，以及它擅長于什么，然后我們將介紹兩個在深度強化學習領域最重要的技術：策略梯度和深度 Q 網絡（DQN），包括討論馬爾可夫決策過程（MDP）。我們將使用這些技術來訓練一個模型來平衡移動車上的桿子，另一個玩 Atari 游戲。同樣的技術可以用于各種各樣的任務，從步行機器人到自動駕駛汽車。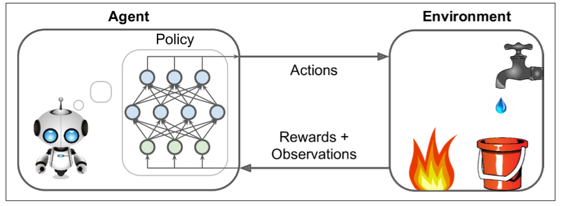 ## 學習優化獎勵 在強化學習中，智能體在環境（environment）中觀察（observation）并且做出決策（action），隨后它會得到獎勵（reward）。它的目標是去學習如何行動能最大化**期望獎勵**。如果你不在意去擬人化的話，你可以認為正獎勵是愉快，負獎勵是痛苦（這樣的話獎勵一詞就有點誤導了）。簡單來說，智能體在環境中行動，并且在實驗和錯誤中去學習最大化它的愉快，最小化它的痛苦。 這是一個相當廣泛的設置，可以適用于各種各樣的任務。以下是幾個例子（詳見圖 16-1）： 1. 智能體可以是控制一個機械狗的程序。在此例中，環境就是真實的世界，智能體通過許多的傳感器例如攝像機或者傳感器來觀察，它可以通過給電機發送信號來行動。它可以被編程設置為如果到達了目的地就得到正獎勵，如果浪費時間，或者走錯方向，或摔倒了就得到負獎勵。 2. 智能體可以是控制 MS.Pac-Man 的程序。在此例中，環境是 Atari 游戲的仿真，行為是 9 個操縱桿位（上下左右中間等等），觀察是屏幕，回報就是游戲點數。 3. 相似地，智能體也可以是棋盤游戲的程序例如：圍棋。 4. 智能體也可以不用去控制一個實體（或虛擬的）去移動。例如它可以是一個智能程序，當它調整到目標溫度以節能時會得到正獎勵，當人們需要自己去調節溫度時它會得到負獎勵，所以智能體必須學會預見人們的需要。 5. 智能體也可以去觀測股票市場價格以實時決定買賣。獎勵的依據顯然為掙錢或者賠錢。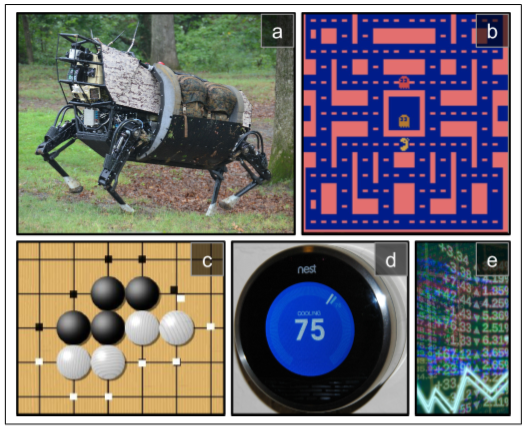  其實沒有正獎勵也是可以的，例如智能體在迷宮內移動，它每分每秒都得到一個負獎勵，所以它要盡可能快的找到出口！還有很多適合強化學習的領域，例如自動駕駛汽車，在網頁上放廣告，或者控制一個圖像分類系統讓它明白它應該關注于什么。 ## 策略搜索 被智能體使用去改變它行為的算法叫做策略。例如，策略可以是一個把觀測當輸入，行為當做輸出的神經網絡（見圖16-2）。  這個策略可以是你能想到的任何算法，它甚至可以不被確定。舉個例子，例如，考慮一個真空吸塵器，它的獎勵是在 30 分鐘內撿起的灰塵數量。它的策略可以是每秒以概率`P`向前移動，或者以概率`1-P`隨機地向左或向右旋轉。旋轉角度將是`-R`和`+R`之間的隨機角度，因為該策略涉及一些隨機性，所以稱為隨機策略。機器人將有一個不確定的軌跡，它保證它最終會到達任何可以到達的地方，并撿起所有的灰塵。問題是：30分鐘后它會撿起多少灰塵？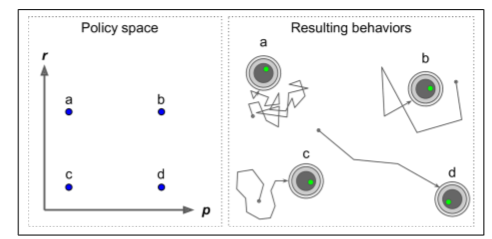 你怎么訓練這樣的機器人？你可以調整兩個策略參數：概率`P`和角度范圍`R`。一個想法是這些參數嘗試許多不同的值，并選擇執行最佳的組合（見圖 16-3）。這是一個策略搜索的例子，在這種情況下使用野蠻的方法。然而，當策略空間太大（通常情況下），以這樣的方式找到一組好的參數就像是大海撈針。  另一種搜尋策略空間的方法是遺傳算法。例如你可以隨機創造一個包含 100 個策略的第一代基因，隨后殺死 80 個糟糕的策略，隨后讓 20 個幸存策略繁衍 4 代。一個后代只是它父輩基因的復制品加上一些隨機變異。幸存的策略加上他們的后代共同構成了第二代。你可以繼續以這種方式迭代代，直到找到一個好的策略。 另一種方法是使用優化技術，通過評估獎勵關于策略參數的梯度，然后通過跟隨梯度向更高的獎勵（梯度上升）調整這些參數。這種方法被稱為策略梯度（policy gradient, PG），我們將在本章后面詳細討論。例如，回到真空吸塵器機器人，你可以稍微增加概率P并評估這是否增加了機器人在 30 分鐘內拾起的灰塵的量；如果確實增加了，就相對應增加`P`，否則減少`P`。我們將使用 Tensorflow 來實現 PG 算法，但是在這之前我們需要為智能體創造一個生存的環境，所以現在是介紹 OpenAI 的時候了。 ## OpenAI 的介紹 強化學習的一個挑戰是，為了訓練智能體，首先需要有一個工作環境。如果你想設計一個可以學習 Atari 游戲的程序，你需要一個 Atari 游戲模擬器。如果你想設計一個步行機器人，那么環境就是真實的世界，你可以直接在這個環境中訓練你的機器人，但是這有其局限性：如果機器人從懸崖上掉下來，你不能僅僅點擊“撤消”。你也不能加快時間；增加更多的計算能力不會讓機器人移動得更快。一般來說，同時訓練 1000 個機器人是非常昂貴的。簡而言之，訓練在現實世界中是困難和緩慢的，所以你通常需要一個模擬環境，至少需要引導訓練。 OpenAI gym 是一個工具包，它提供各種各樣的模擬環境（Atari 游戲，棋盤游戲，2D 和 3D 物理模擬等等），所以你可以訓練，比較，或開發新的 RL 算法。 讓我們安裝 OpenAI gym。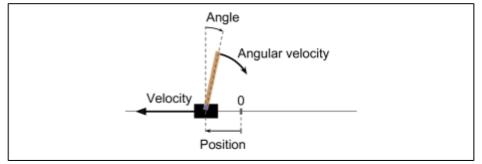可通過`pip`安裝： ```bash $ pip install --upgrade gym ``` 接下來打開 Python shell 或 Jupyter 筆記本創建您的第一個環境： ```python >>> import gym >>> env = gym.make("CartPole-v0") [2016-10-14 16:03:23,199] Making new env: MsPacman-v0 >>> obs = env.reset() >>> obs array([-0.03799846,-0.03288115,0.02337094,0.00720711]) >>> env.render() ``` 使用`make()`函數創建一個環境，在此例中是 CartPole 環境。這是一個 2D 模擬，其中推車可以被左右加速，以平衡放置在它上面的平衡桿（見圖 16-4）。在創建環境之后，我們需要使用`reset()`初始化。這會返回第一個觀察結果。觀察取決于環境的類型。對于 CartPole 環境，每個觀測是包含四個浮點的 1D Numpy 向量：這些浮點數代表推車的水平位置（0 為中心）、其速度、桿的角度（0 維垂直）及其角速度。最后，`render()`方法顯示如圖 16-4 所示的環境。  如果你想讓`render()`讓圖像以一個 NUMPY 數組格式返回，可以將`mode`參數設置為`rgb_array`（注意其他環境可能支持不同的模式）： ```python >>> img = env.render(mode="rgb_array") >>> img.shape # height, width, channels (3=RGB) (400, 600, 3) ``` 不幸的是，即使將`mode`參數設置為`rgb_array`，CartPole（和其他一些環境）還是會將將圖像呈現到屏幕上。避免這種情況的唯一方式是使用一個 fake X 服務器，如 XVFB 或 XDimMy。例如，可以使用以下命令安裝 XVFB 和啟動 Python：`xvfb-run -s "screen 0 1400x900x24" python`。或者使用`xvfbwrapper`包。 讓我們來詢問環境什么動作是可能的： ```python >>> env.action_space Discrete(2) ``` `Discrete(2)`表示可能的動作是整數 0 和 1，表示向左（0）或右（1）的加速。其他環境可能有更多的動作，或者其他類型的動作（例如，連續的）。因為桿子向右傾斜，讓我們向右加速推車： ```python >>> action = 1 # accelerate right >>> obs, reward, done, info = env.step(action) >>> obs array([-0.03865608, 0.16189797, 0.02351508, -0.27801135]) >>> reward 1.0 >>> done False >>> info {} ``` `step()`表示執行給定的動作并返回四個值： `obs`: 這是新的觀測，小車現在正在向右走（`obs[1]>0`，注：當前速度為正，向右為正）。平衡桿仍然向右傾斜（`obs[2]>0`），但是他的角速度現在為負（`obs[3]<0`），所以它在下一步后可能會向左傾斜。 `reward`： 在這個環境中，無論你做什么，每一步都會得到 1.0 獎勵，所以游戲的目標就是盡可能長的運行。 `done`： 當游戲結束時這個值會為`True`。當平衡桿傾斜太多時會發生這種情況。之后，必須重新設置環境才能重新使用。 `info`： 該字典可以在其他環境中提供額外的調試信息。這些數據不應該用于訓練（這是作弊）。 讓我們硬編碼一個簡單的策略，當桿向左傾斜時加速左邊，當桿向右傾斜時加速。我們使用這個策略來獲得超過 500 步的平均回報： ```python def basic_policy(obs): angle = obs[2] return 0 if angle < 0 else 1 totals = [] for episode in range(500): episode_rewards = 0 obs = env.reset() for step in range(1000): # 最多1000 步，我們不想讓它永遠運行下去 action = basic_policy(obs) obs, reward, done, info = env.step(action) episode_rewards += reward if done: break totals.append(episode_rewards) ``` 這個代碼希望能自我解釋。讓我們看看結果： ```python >>> import numpy as np >>> np.mean(totals), np.std(totals), np.min(totals), np.max(totals) (42.125999999999998, 9.1237121830974033, 24.0, 68.0) ``` 即使有 500 次嘗試，這一策略從未使平衡桿在超過 68 個連續的步驟里保持直立。這不太好。如果你看一下 Juyter Notebook 中的模擬，你會發現，推車越來越強烈地左右擺動，直到平衡桿傾斜太多。讓我們看看神經網絡是否能提出更好的策略。 ## 神經網絡策略 讓我們創建一個神經網絡策略。就像之前我們編碼的策略一樣，這個神經網絡將把觀察作為輸入，輸出要執行的動作。更確切地說，它將估計每個動作的概率，然后我們將根據估計的概率隨機地選擇一個動作（見圖 16-5）。在 CartPole 環境中，只有兩種可能的動作（左或右），所以我們只需要一個輸出神經元。它將輸出動作 0（左）的概率`p`，動作 1（右）的概率顯然將是`1 - p`。 例如，如果它輸出 0.7，那么我們將以 70% 的概率選擇動作 0，以 30% 的概率選擇動作 1。  你可能奇怪為什么我們根據神經網絡給出的概率來選擇隨機的動作，而不是選擇最高分數的動作。這種方法使智能體在**探索新的行為**和**利用那些已知可行的行動**之間找到正確的平衡。舉個例子：假設你第一次去餐館，所有的菜看起來同樣吸引人，所以你隨機挑選一個。如果菜好吃，你可以增加下一次點它的概率，但是你不應該把這個概率提高到 100%，否則你將永遠不會嘗試其他菜肴，其中一些甚至比你嘗試的更好。 還要注意，在這個特定的環境中，過去的動作和觀察可以被安全地忽略，因為每個觀察都包含環境的完整狀態。如果有一些隱藏狀態，那么你也需要考慮過去的行為和觀察。例如，如果環境僅僅揭示了推車的位置，而不是它的速度，那么你不僅要考慮當前的觀測，還要考慮先前的觀測，以便估計當前的速度。另一個例子是當觀測是有噪聲的的，在這種情況下，通常你想用過去的觀察來估計最可能的當前狀態。因此，CartPole 問題是簡單的；觀測是無噪聲的，而且它們包含環境的全狀態。 ```python import tensorflow as tf from tensorflow.contrib.layers import fully_connected # 1. 聲明神經網絡結構 n_inputs = 4 # == env.observation_space.shape[0] n_hidden = 4 # 這只是個簡單的測試，不需要過多的隱藏層 n_outputs = 1 # 只輸出向左加速的概率 initializer = tf.contrib.layers.variance_scaling_initializer() # 2. 建立神經網絡 X = tf.placeholder(tf.float32, shape=[None, n_inputs]) hidden = fully_connected(X, n_hidden, activation_fn=tf.nn.elu,weights_initializer=initializer) # 隱層激活函數使用指數線性函數 logits = fully_connected(hidden, n_outputs, activation_fn=None,weights_initializer=initializer) outputs = tf.nn.sigmoid(logits) # 3. 在概率基礎上隨機選擇動作 p_left_and_right = tf.concat(axis=1, values=[outputs, 1 - outputs]) action = tf.multinomial(tf.log(p_left_and_right), num_samples=1) init = tf.global_variables_initializer() ``` 讓我們通讀代碼： 1. 在導入之后，我們定義了神經網絡體系結構。輸入的數量是觀測空間的大小（在 CartPole 的情況下是 4 個），我們只有 4 個隱藏單元，并且不需要更多，并且我們只有 1 個輸出概率（向左的概率）。 2. 接下來我們構建了神經網絡。在這個例子中，它是一個 vanilla 多層感知器，只有一個輸出。注意，輸出層使用 Logistic（Sigmoid）激活函數，以便輸出從 0 到 1 的概率。如果有兩個以上的可能動作，每個動作都會有一個輸出神經元，相應的你將使用 Softmax 激活函數。 3. 最后，我們調用`multinomial()`函數來選擇一個隨機動作。該函數獨立地采樣一個（或多個）整數，給定每個整數的對數概率。例如，如果通過設置`num_samples=5`，令數組為`[np.log(0.5), np.log(0.2), np.log(0.3)]`來調用它，那么它將輸出五個整數，每個整數都有 50% 的概率是 0，20% 為 1，30% 為 2。在我們的情況下，我們只需要一個整數來表示要采取的行動。由于輸出張量（output）僅包含向左的概率，所以我們必須首先將 1 - output 連接它，以得到包含左和右動作的概率的張量。請注意，如果有兩個以上的可能動作，神經網絡將不得不輸出每個動作的概率，這時你就不需要連接步驟了。 好了，現在我們有一個可以觀察和輸出動作的神經網絡了，那我們怎么訓練它呢？ ## 評價行為：信用分配問題 如果我們知道每一步的最佳動作，我們可以像通常一樣訓練神經網絡，通過最小化估計概率和目標概率之間的交叉熵。這只是通常的監督學習。然而，在強化學習中，智能體獲得的指導的唯一途徑是通過獎勵，獎勵通常是稀疏的和延遲的。例如，如果智能體在 100 個步驟內設法平衡桿，它怎么知道它采取的 100 個行動中的哪一個是好的，哪些是壞的？它所知道的是，在最后一次行動之后，桿子墜落了，但最后一次行動肯定不是完全負責的。這被稱為信用分配問題：當智能體得到獎勵時，很難知道哪些行為應該被信任（或責備）。想想一只狗在行為良好后幾小時就會得到獎勵，它會明白它得到了什么回報嗎？ 為了解決這個問題，一個通常的策略是基于這個動作后得分的總和來評估這個個動作，通常在每個步驟中應用衰減率`r`。例如（見圖 16-6），如果一個智能體決定連續三次向右，在第一步之后得到 +10 獎勵，第二步后得到 0，最后在第三步之后得到 -50，然后假設我們使用衰減率`r=0.8`，那么第一個動作將得到`10 +r×0 + r2×(-50)=-22`的分述。如果衰減率接近 0，那么與即時獎勵相比，未來的獎勵不會有多大意義。相反，如果衰減率接近 1，那么對未來的獎勵幾乎等于即時回報。典型的衰減率通常為是 0.95 或 0.99。如果衰減率為 0.95，那么未來 13 步的獎勵大約是即時獎勵的一半（`0.9513×0.5`），而當衰減率為 0.99，未來 69 步的獎勵是即時獎勵的一半。在 CartPole 環境下，行為具有相當短期的影響，因此選擇 0.95 的折扣率是合理的。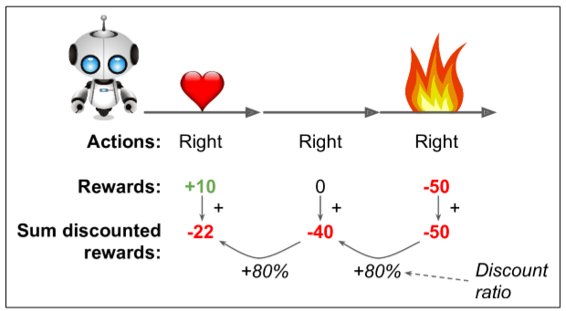  當然，一個好的動作可能會伴隨著一些壞的動作，這些動作會導致平衡桿迅速下降，從而導致一個好的動作得到一個低分數（類似的，一個好行動者有時會在一部爛片中扮演主角）。然而，如果我們花足夠多的時間來訓練游戲，平均下來好的行為會得到比壞的更好的分數。因此，為了獲得相當可靠的動作分數，我們必須運行很多次并將所有動作分數歸一化（通過減去平均值并除以標準偏差）。之后，我們可以合理地假設消極得分的行為是壞的，而積極得分的行為是好的。現在我們有一個方法來評估每一個動作，我們已經準備好使用策略梯度來訓練我們的第一個智能體。讓我們看看如何。 ## 策略梯度 正如前面所討論的，PG 算法通過遵循更高回報的梯度來優化策略參數。一種流行的 PG 算法，稱為增強算法，在 1929 由 Ronald Williams 提出。這是一個常見的變體： 1. 首先，讓神經網絡策略玩幾次游戲，并在每一步計算梯度，這使得智能體更可能選擇行為，但不應用這些梯度。 2. 運行幾次后，計算每個動作的得分（使用前面段落中描述的方法）。 3. 如果一個動作的分數是正的，這意味著動作是好的，可應用較早計算的梯度，以便將來有更大的的概率選擇這個動作。但是，如果分數是負的，這意味著動作是壞的，要應用負梯度來使得這個動作在將來采取的可能性更低。我們的方法就是簡單地將每個梯度向量乘以相應的動作得分。 4. 最后，計算所有得到的梯度向量的平均值，并使用它來執行梯度下降步驟。 讓我們使用 TensorFlow 實現這個算法。我們將訓練我們早先建立的神經網絡策略，讓它學會平衡車上的平衡桿。讓我們從完成之前編碼的構造階段開始，添加目標概率、代價函數和訓練操作。因為我們的意愿是選擇的動作是最好的動作，如果選擇的動作是動作 0（左），則目標概率必須為 1，如果選擇動作 1（右）則目標概率為 0： ```python y = 1. - tf.to_float(action) ``` 現在我們有一個目標概率，我們可以定義損失函數（交叉熵）并計算梯度： ```python learning_rate = 0.01 cross_entropy = tf.nn.sigmoid_cross_entropy_with_logits( labels=y, logits=logits) optimizer = tf.train.AdamOptimizer(learning_rate) grads_and_vars = optimizer.compute_gradients(cross_entropy) ``` 注意，我們正在調用優化器的`compute_gradients()`方法，而不是`minimize()`方法。這是因為我們想要在使用它們之前調整梯度。`compute_gradients()`方法返回梯度向量/變量對的列表（每個可訓練變量一對）。讓我們把所有的梯度放在一個列表中，以便方便地獲得它們的值： ```python gradients = [grad for grad, variable in grads_and_vars] ``` 好，現在是棘手的部分。在執行階段，算法將運行策略，并在每個步驟中評估這些梯度張量并存儲它們的值。在多次運行之后，它如先前所解釋的調整這些梯度（即，通過動作分數乘以它們并使它們歸一化），并計算調整后的梯度的平均值。接下來，需要將結果梯度反饋到優化器，以便它可以執行優化步驟。這意味著對于每一個梯度向量我們需要一個占位符。此外，我們必須創建操作去應用更新的梯度。為此，我們將調用優化器的`apply_gradients()`函數，該函數接受梯度向量/變量對的列表。我們不給它原始的梯度向量，而是給它一個包含更新梯度的列表（即，通過占位符遞送的梯度）： ```python gradient_placeholders = [] grads_and_vars_feed = [] for grad, variable in grads_and_vars: gradient_placeholder = tf.placeholder(tf.float32, shape=grad.get_shape()) gradient_placeholders.append(gradient_placeholder) grads_and_vars_feed.append((gradient_placeholder, variable)) training_op = optimizer.apply_gradients(grads_and_vars_feed) ``` 讓我們后退一步，看看整個運行過程： ```python n_inputs = 4 n_hidden = 4 n_outputs = 1 initializer = tf.contrib.layers.variance_scaling_initializer() learning_rate = 0.01 X = tf.placeholder(tf.float32, shape=[None, n_inputs]) hidden = fully_connected(X, n_hidden, activation_fn=tf.nn.elu,weights_initializer=initializer) logits = fully_connected(hidden, n_outputs, activation_fn=None, weights_initializer=initializer) outputs = tf.nn.sigmoid(logits) p_left_and_right = tf.concat(axis=1, values=[outputs, 1 - outputs]) action = tf.multinomial(tf.log(p_left_and_right), num_samples=1) y = 1. - tf.to_float(action) cross_entropy = tf.nn.sigmoid_cross_entropy_with_logits(labels=y, logits=logits) optimizer = tf.train.AdamOptimizer(learning_rate) grads_and_vars = optimizer.compute_gradients(cross_entropy) gradients = [grad for grad, variable in grads_and_vars] gradient_placeholders = [] grads_and_vars_feed = [] for grad, variable in grads_and_vars: gradient_placeholder = tf.placeholder(tf.float32, shape=grad.get_shape()) gradient_placeholders.append(gradient_placeholder) grads_and_vars_feed.append((gradient_placeholder, variable)) training_op = optimizer.apply_gradients(grads_and_vars_feed) init = tf.global_variables_initializer() saver = tf.train.Saver() ``` 到執行階段了！我們將需要兩個函數來計算總折扣獎勵，給予原始獎勵，以及歸一化多次循環的結果： ```python def discount_rewards(rewards, discount_rate): discounted_rewards = np.empty(len(rewards)) cumulative_rewards = 0 for step in reversed(range(len(rewards))): cumulative_rewards = rewards[step] + cumulative_rewards * discount_rate discounted_rewards[step] = cumulative_rewards return discounted_rewards def discount_and_normalize_rewards(all_rewards, discount_rate): all_discounted_rewards = [discount_rewards(rewards) for rewards in all_rewards] flat_rewards = np.concatenate(all_discounted_rewards) reward_mean = flat_rewards.mean() reward_std = flat_rewards.std() return [(discounted_rewards - reward_mean)/reward_std for discounted_rewards in all_discounted_rewards] ``` 讓我們檢查一下運行的如何： ```python >>> discount_rewards([10, 0, -50], discount_rate=0.8) array([-22., -40., -50.]) >>> discount_and_normalize_rewards([[10, 0, -50], [10, 20]], discount_rate=0.8) [array([-0.28435071, -0.86597718, -1.18910299]), array([ 1.26665318, 1.0727777 ])] ``` 對`discount_rewards()`的調用正好返回我們所期望的（見圖 16-6）。你也可以驗證函數`iscount_and_normalize_rewards()`確實返回了兩個步驟中每個動作的標準化分數。注意第一步比第二步差很多，所以它的歸一化分數都是負的；從第一步開始的所有動作都會被認為是壞的，反之，第二步的所有動作都會被認為是好的。 我們現在有了訓練策略所需的一切： ```python n_iterations = 250 # 訓練迭代次數 n_max_steps = 1000 # 每一次的最大步長 n_games_per_update = 10 # 每迭代十次訓練一次策略網絡 save_iterations = 10 # 每十次迭代保存模型 discount_rate = 0.95 with tf.Session() as sess: init.run() for iteration in range(n_iterations): all_rewards = [] #每一次的所有獎勵 all_gradients = [] #每一次的所有梯度 for game in range(n_games_per_update): current_rewards = [] #當前步的所有獎勵 current_gradients = [] #當前步的所有梯度 obs = env.reset() for step in range(n_max_steps): action_val, gradients_val = sess.run([action, gradients], feed_dict={X: obs.reshape(1, n_inputs)}) # 一個obs obs, reward, done, info = env.step(action_val[0][0]) current_rewards.append(reward) current_gradients.append(gradients_val) if done: break all_rewards.append(current_rewards) all_gradients.append(current_gradients) # 此時我們每10次運行一次策略，我們已經準備好使用之前描述的算法去更新策略，注：即使用迭代10次的結果來優化當前的策略。 all_rewards = discount_and_normalize_rewards(all_rewards) feed_dict = {} for var_index, grad_placeholder in enumerate(gradient_placeholders): # 將梯度與行為分數相乘，并計算平均值 mean_gradients = np.mean([reward * all_gradients[game_index][step][var_index] for game_index, rewards in enumerate(all_rewards) for step, reward in enumerate(rewards)],axis=0) feed_dict[grad_placeholder] = mean_gradients sess.run(training_op, feed_dict=feed_dict) if iteration % save_iterations == 0: saver.save(sess, "./my_policy_net_pg.ckpt") ``` 每一次訓練迭代都是通過運行10次的策略開始的（每次最多 1000 步，以避免永遠運行）。在每一步，我們也計算梯度，假設選擇的行動是最好的。在運行了這 10 次之后，我們使用`discount_and_normalize_rewards()`函數計算動作得分；我們遍歷每個可訓練變量，在所有次數和所有步驟中，通過其相應的動作分數來乘以每個梯度向量；并且我們計算結果的平均值。最后，我們運行訓練操作，給它提供平均梯度（對每個可訓練變量提供一個）。我們繼續每 10 個訓練次數保存一次模型。 我們做完了！這段代碼將訓練神經網絡策略，它將成功地學會平衡車上的平衡桿（你可以在 Juyter notebook 上試用）。注意，實際上有兩種方法可以讓玩家游戲結束：要么平衡可以傾斜太大，要么車完全脫離屏幕。在 250 次訓練迭代中，策略學會平衡極點，但在避免脫離屏幕方面還不夠好。額外數百次的訓練迭代可以解決這一問題。 研究人員試圖找到一種即使當智能體最初對環境一無所知時也能很好地工作的算法。然而，除非你正在寫論文，否則你應該盡可能多地將先前的知識注入到智能體中，因為它會極大地加速訓練。例如，你可以添加與屏幕中心距離和極點角度成正比的負獎勵。此外，如果你已經有一個相當好的策略，你可以訓練神經網絡模仿它，然后使用策略梯度來改進它。 盡管它相對簡單，但是該算法是非常強大的。你可以用它來解決更難的問題，而不僅僅是平衡一輛手推車上的平衡桿。事實上，AlgPaGo 是基于類似的 PG 算法（加上蒙特卡羅樹搜索，這超出了本書的范圍）。 現在我們來看看另一個流行的算法。與 PG 算法直接嘗試優化策略以增加獎勵相反，我們現在看的算法是間接的：智能體學習去估計每個狀態的未來衰減獎勵的期望總和，或者在每個狀態中的每個行為未來衰減獎勵的期望和。然后，使用這些知識來決定如何行動。為了理解這些算法，我們必須首先介紹馬爾可夫決策過程（MDP）。 ## 馬爾可夫決策過程 在二十世紀初，數學家 Andrey Markov 研究了沒有記憶的隨機過程，稱為馬爾可夫鏈。這樣的過程具有固定數量的狀態，并且在每個步驟中隨機地從一個狀態演化到另一個狀態。它從狀態`S`演變為狀態`S'`的概率是固定的，它只依賴于`(S, S')`對，而不是依賴于過去的狀態（系統沒有記憶）。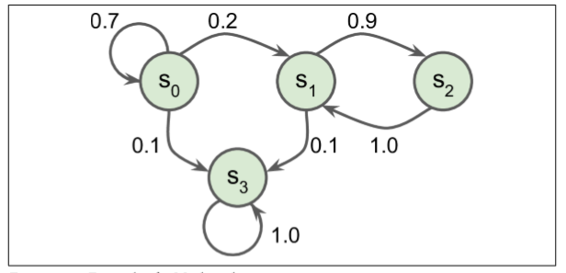 圖 16-7 展示了一個具有四個狀態的馬爾可夫鏈的例子。假設該過程從狀態`S0`開始，并且在下一步驟中有 70% 的概率保持在該狀態不變中。最終，它必然離開那個狀態，并且永遠不會回來，因為沒有其他狀態回到`S0`。如果它進入狀態`S1`，那么它很可能會進入狀態`S2`（90% 的概率），然后立即回到狀態`S1`（以 100% 的概率）。它可以在這兩個狀態之間交替多次，但最終它會落入狀態`S3`并永遠留在那里（這是一個終端狀態）。馬爾可夫鏈可以有非常不同的應用，它們在熱力學、化學、統計學等方面有著廣泛的應用。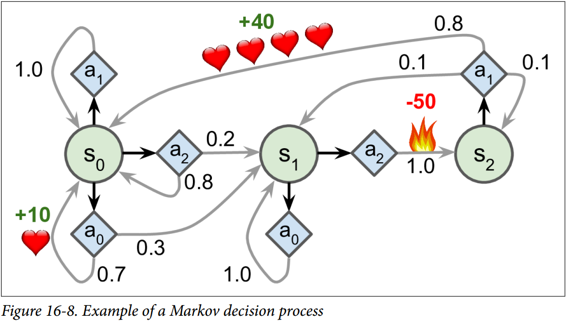  馬爾可夫決策過程最初是在 20 世紀 50 年代由 Richard Bellman 描述的。它們類似于馬爾可夫鏈，但有一個連結：**在狀態轉移的每一步中，一個智能體可以選擇幾種可能的動作中的一個，并且轉移概率取決于所選擇的動作。**此外，一些狀態轉移返回一些獎勵（正或負），智能體的目標是找到一個策略，隨著時間的推移將最大限度地提高獎勵。 例如，圖 16-8 中所示的 MDP 在每個步驟中具有三個狀態和三個可能的離散動作。如果從狀態`S0`開始，隨著時間的推移可以在動作`A0`、`A1`或`A2`之間進行選擇。如果它選擇動作`A1`，它就保持在狀態`S0`中，并且沒有任何獎勵。因此，如果愿意的話，它可以決定永遠呆在那里。但是，如果它選擇動作`A0`，它有 70% 的概率獲得 10 獎勵，并保持在狀態`S0`。然后，它可以一次又一次地嘗試獲得盡可能多的獎勵。但它將在狀態`S1`中結束這樣的行為。在狀態`S1`中，它只有兩種可能的動作：`A0`或`A1`。它可以通過反復選擇動作`A1`來選擇停留，或者它可以選擇動作`A2`移動到狀態`S2`并得到 -50 獎勵。在狀態`S3`中，除了采取行動`A1`之外，別無選擇，這將最有可能引導它回到狀態`S0`，在途中獲得 40 的獎勵。通過觀察這個 MDP，你能猜出哪一個策略會隨著時間的推移而獲得最大的回報嗎？在狀態`S0`中，清楚地知道`A0`是最好的選擇，在狀態`S3`中，智能體別無選擇，只能采取行動`A1`，但是在狀態`S1`中，智能體否應該保持不動（`A0`）或通過火（`A2`），這是不明確的。  Bellman 找到了一種估計任何狀態`S`的最佳狀態值的方法，他提出了`V(s)`，它是智能體在其采取最佳行為達到狀態`s`后所有衰減未來獎勵的總和的平均期望。他表明，如果智能體的行為最佳，那么貝爾曼最優性公式適用（見公式 16-1）。這個遞歸公式表示，如果智能體最優地運行，那么當前狀態的最優值等于在采取一個最優動作之后平均得到的獎勵，加上該動作可能導致的所有可能的下一個狀態的期望最優值。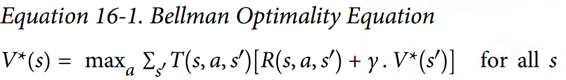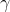  其中： + `T`為智能體選擇動作`a`時從狀態`s`到狀態`s'`的概率 + `R`為智能體選擇以動作`a`從狀態`s`到狀態`s'`的過程中得到的獎勵 + 為衰減率 這個等式直接引出了一種算法，該算法可以精確估計每個可能狀態的最優狀態值：首先將所有狀態值估計初始化為零，然后用數值迭代算法迭代更新它們（見公式 16-2）。一個顯著的結果是，給定足夠的時間，這些估計保證收斂到最優狀態值，對應于最優策略。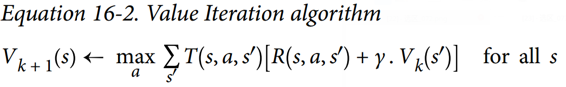  其中： + 是在`k`次算法迭代對狀態`s`的估計 該算法是動態規劃的一個例子，它將了一個復雜的問題（在這種情況下，估計潛在的未來衰減獎勵的總和）變為可處理的子問題，可以迭代地處理（在這種情況下，找到最大化平均報酬與下一個衰減狀態值的和的動作） 了解最佳狀態值可能是有用的，特別是評估策略，但它沒有明確地告訴智能體要做什么。幸運的是，Bellman 發現了一種非常類似的算法來估計最優狀態-動作值（*state-action values*），通常稱為 Q 值。狀態行動`(S, A)`對的最優 Q 值，記為`Q(s, a)`，是智能體在到達狀態`S`，然后選擇動作`A`之后平均衰減未來獎勵的期望的總和。但是在它看到這個動作的結果之前，假設它在該動作之后的動作是最優的。 下面是它的工作原理：再次，通過初始化所有的 Q 值估計為零，然后使用 Q 值迭代算法更新它們（參見公式 16-3）。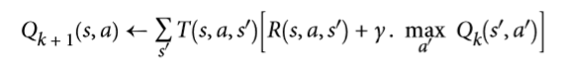  一旦你有了最佳的 Q 值，定義最優的策略`π*(s)`，它是平凡的：當智能體處于狀態`S`時，它應該選擇具有最高 Q 值的動作，用于該狀態：。 讓我們把這個算法應用到圖 16-8 所示的 MDP 中。首先，我們需要定義 MDP： ```python nan=np.nan # 代表不可能的動作 T = np.array([ # shape=[s, a, s'] [[0.7, 0.3, 0.0], [1.0, 0.0, 0.0], [0.8, 0.2, 0.0]], [[0.0, 1.0, 0.0], [nan, nan, nan], [0.0, 0.0, 1.0]], [[nan, nan, nan], [0.8, 0.1, 0.1], [nan, nan, nan]], ]) R = np.array([ # shape=[s, a, s'] [[10., 0.0, 0.0], [0.0, 0.0, 0.0], [0.0, 0.0, 0.0]], [[10., 0.0, 0.0], [nan, nan, nan], [0.0, 0.0, -50.]], [[nan, nan, nan], [40., 0.0, 0.0], [nan, nan, nan]], ]) possible_actions = [[0, 1, 2], [0, 2], [1]] ``` 讓我們運行 Q 值迭代算法 ```python Q = np.full((3, 3), -np.inf) # -inf 對應著不可能的動作 for state, actions in enumerate(possible_actions): Q[state, actions] = 0.0 # 對所有可能的動作初始化為0.0 learning_rate = 0.01 discount_rate = 0.95 n_iterations = 100 for iteration in range(n_iterations): Q_prev = Q.copy() for s in range(3): for a in possible_actions[s]: Q[s, a] = np.sum([T[s, a, sp] * (R[s, a, sp] + discount_rate * np.max(Q_prev[sp])) for sp in range(3)]) ``` 結果的 Q 值類似于如下： ```python >>> Q array([[ 21.89498982, 20.80024033, 16.86353093], [ 1.11669335, -inf, 1.17573546], [ -inf, 53.86946068, -inf]]) >>> np.argmax(Q, axis=1) # 每一狀態的最優動作 array([0, 2, 1]) ``` 這給我們這個 MDP 的最佳策略，當使用 0.95 的衰減率時：在狀態`S0`選擇動作`A0`，在狀態`S1`選擇動作`A2`（通過火焰！）在狀態`S2`中選擇動作`A1`（唯一可能的動作）。有趣的是，如果你把衰減率降低到 0.9，最優的策略改變：在狀態`S1`中，最好的動作變成`A0`（保持不變；不通過火）。這是有道理的，因為如果你認為現在比未來更重要，那么未來獎勵的前景是不值得立刻經歷痛苦的。 ## 時間差分學習與 Q 學習 具有離散動作的強化學習問題通常可以被建模為馬爾可夫決策過程，但是智能體最初不知道轉移概率是什么（它不知道`T`），并且它不知道獎勵會是什么（它不知道`R`）。它必須經歷每一個狀態和每一次轉變并且至少知道一次獎勵，并且如果要對轉移概率進行合理的估計，就必須經歷多次。 時間差分學習（TD 學習）算法與數值迭代算法非常類似，但考慮到智能體僅具有 MDP 的部分知識。一般來說，我們假設智能體最初只知道可能的狀態和動作，沒有更多了。智能體使用探索策略，例如，純粹的隨機策略來探索 MDP，并且隨著它的發展，TD 學習算法基于實際觀察到的轉換和獎勵來更新狀態值的估計（見公式 16-4）。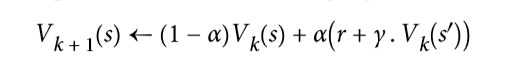  其中： `a`是學習率（例如 0.01） TD 學習與隨機梯度下降有許多相似之處，特別是它一次處理一個樣本的行為。就像 SGD 一樣，只有當你逐漸降低學習速率時，它才能真正收斂（否則它將在極值點震蕩）。 對于每個狀態`S`，該算法只跟蹤智能體離開該狀態時立即獲得的獎勵的平均值，再加上它期望稍后得到的獎勵（假設它的行為最佳）。 類似地，此時的Q 學習算法是 Q 值迭代算法的改編版本，其適應轉移概率和回報在初始未知的情況（見公式16-5）。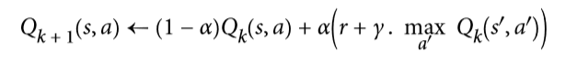  對于每一個狀態動作對`(s,a)`，該算法跟蹤智能體在以動作`A`離開狀態`S`時獲得的即時獎勵平均值`R`，加上它期望稍后得到的獎勵。由于目標策略將最優地運行，所以我們取下一狀態的 Q 值估計的最大值。 以下是如何實現 Q 學習： ```python import numpy.random as rnd learning_rate0 = 0.05 learning_rate_decay = 0.1 n_iterations = 20000 s = 0 # 在狀態 0開始 Q = np.full((3, 3), -np.inf) # -inf 對應著不可能的動作 for state, actions in enumerate(possible_actions): Q[state, actions] = 0.0 # 對于所有可能的動作初始化為 0.0 for iteration in range(n_iterations): a = rnd.choice(possible_actions[s]) # 隨機選擇動作 sp = rnd.choice(range(3), p=T[s, a]) # 使用 T[s, a] 挑選下一狀態 reward = R[s, a, sp] learning_rate = learning_rate0 / (1 + iteration * learning_rate_decay) Q[s, a] = learning_rate * Q[s, a] + (1 - learning_rate) * (reward + discount_rate * np.max(Q[sp])) s = sp # 移動至下一狀態 ``` 給定足夠的迭代，該算法將收斂到最優 Q 值。這被稱為離線策略算法，因為正在訓練的策略不是正在執行的策略。令人驚訝的是，該算法能夠通過觀察智能體行為隨機學習（例如學習當你的老師是一個醉猴子時打高爾夫球）最佳策略。我們能做得更好嗎？ ## 探索策略 當然，只有在探索策略充分探索 MDP 的情況下，Q 學習才能起作用。盡管一個純粹的隨機策略保證最終訪問每一個狀態和每個轉換多次，但可能需要很長的時間這樣做。因此，一個更好的選擇是使用 ε 貪婪策略：在每個步驟中，它以概率`ε`隨機地或以概率為`1-ε`貪婪地（選擇具有最高 Q 值的動作）。ε 貪婪策略的優點（與完全隨機策略相比）是，它將花費越來越多的時間來探索環境中有趣的部分，因為 Q 值估計越來越好，同時仍花費一些時間訪問 MDP 的未知區域。以`ε`為很高的值（例如，1）開始，然后逐漸減小它（例如，下降到 0.05）是很常見的。 可選擇的，相比于依賴于探索的可能性，另一種方法是鼓勵探索策略來嘗試它以前沒有嘗試過的行動。這可以被實現為附加于 Q 值估計的獎金，如公式 16-6 所示。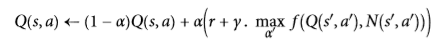  其中： + `N`計算了在狀態`s`時選擇動作`a`的次數 + `f`是一個探索函數，例如`f=q+K/(1+n)`，其中`K`是一個好奇超參數，它測量智能體被吸引到未知狀態的程度。 ## 近似 Q 學習 Q 學習的主要問題是，它不能很好地擴展到具有許多狀態和動作的大（甚至中等）的 MDP。試著用 Q 學習來訓練一個智能體去玩 Ms. Pac-Man。Ms. Pac-Man 可以吃超過 250 粒粒子，每一粒都可以存在或不存在（即已經吃過）。因此，可能狀態的數目大于 2 的 250 次冪，約等于 10 的 75 次冪（并且這是考慮顆粒的可能狀態）。這比在可觀測的宇宙中的原子要多得多，所以你絕對無法追蹤每一個 Q 值的估計值。 解決方案是找到一個函數，使用可管理數量的參數來近似 Q 值。這被稱為近似 Q 學習。多年來，人們都是手工在狀態中提取并線性組合特征（例如，最近的鬼的距離，它們的方向等）來估計 Q 值，但是 DeepMind 表明使用深度神經網絡可以工作得更好，特別是對于復雜的問題。它不需要任何特征工程。用于估計 Q 值的 DNN 被稱為深度 Q 網絡（DQN），并且使用近似 Q 學習的 DQN 被稱為深度 Q 學習。 在本章的剩余部分，我們將使用深度 Q 學習來訓練一個智能體去玩 Ms. Pac-Man，就像 DeepMind 在 2013 所做的那樣。代碼可以很容易地調整，調整后學習去玩大多數 Atari 游戲的效果都相當好。在大多數動作游戲中，它可以達到超人的技能，但它在長時運行的游戲中卻不太好。 ## 學習去使用深度 Q 學習來玩 Ms.Pac-Man 由于我們將使用 Atari 環境，我們必須首先安裝 OpenAI gym 的 Atari 環境依賴項。當需要玩其他的時候，我們也會為你想玩的其他 OpenAI gym 環境安裝依賴項。在 macOS 上，假設你已經安裝了 Homebrew 程序，你需要運行： ``` $ brew install cmake boost boost-python sdl2 swig wget ``` 在 Ubuntu 上，輸入以下命令（如果使用 Python 2，用 Python 替換 Python 3）： ``` $ apt-get install -y python3-numpy python3-dev cmake zlib1g-dev libjpeg-dev\ xvfb libav-tools xorg-dev python3-opengl libboost-all-dev libsdl2-dev swig ``` 隨后安裝額外的 python 包： ``` $ pip3 install --upgrade 'gym[all]' ``` 如果一切順利，你應該能夠創造一個 Ms.Pac-Man 環境： ```python >>> env = gym.make("MsPacman-v0") >>> obs = env.reset() >>> obs.shape # [長，寬，通道] (210, 160, 3) >>> env.action_space Discrete(9) ``` 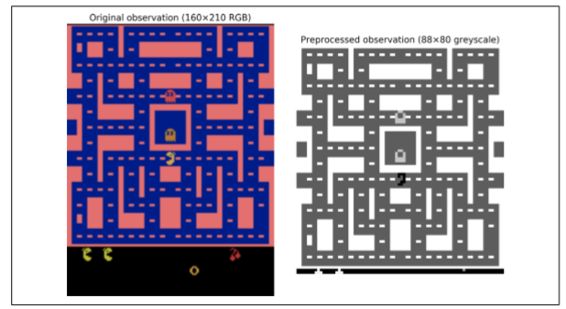正如你所看到的，有九個離散動作可用，它對應于操縱桿的九個可能位置（左、右、上、下、中、左上等），觀察結果是 Atari 屏幕的截圖（見圖 16-9，左），表示為 3D Numpy 矩陣。這些圖像有點大，所以我們將創建一個小的預處理函數，將圖像裁剪并縮小到`88×80`像素，將其轉換成灰度，并提高 Ms.Pac-Man 的對比度。這將減少 DQN 所需的計算量，并加快培訓練。 ```python mspacman_color = np.array([210, 164, 74]).mean() def preprocess_observation(obs): img = obs[1:176:2, ::2] # 裁剪 img = img.mean(axis=2) # 灰度化 img[img==mspacman_color] = 0 # 提升對比度 img = (img - 128) / 128 - 1 # 正則化為-1到1. return img.reshape(88, 80, 1) ``` 過程的結果如圖 16-9 所示（右）。  接下來，讓我們創建 DQN。它可以只取一個狀態動作對`(S,A)`作為輸入，并輸出相應的 Q 值`Q(s,a)`的估計值，但是由于動作是離散的，所以使用只使用狀態`S`作為輸入并輸出每個動作的一個 Q 值估計的神經網絡是更方便的。DQN 將由三個卷積層組成，接著是兩個全連接層，其中包括輸出層（如圖 16-10）。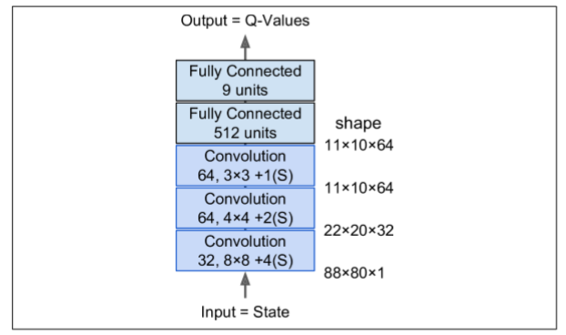  正如我們將看到的，我們將使用的訓練算法需要兩個具有相同架構（但不同參數）的 DQN：一個將在訓練期間用于驅動 Ms.Pac-Man（the *actor*，行動者），另一個將觀看行動者并從其試驗和錯誤中學習（the *critic*，評判者）。每隔一定時間，我們把評判者網絡復制給行動者網絡。因為我們需要兩個相同的 DQN，所以我們將創建一個`q_network()`函數來構建它們： ```python from tensorflow.contrib.layers import convolution2d, fully_connected input_height = 88 input_width = 80 input_channels = 1 conv_n_maps = [32, 64, 64] conv_kernel_sizes = [(8,8), (4,4), (3,3)] conv_strides = [4, 2, 1] conv_paddings = ["SAME"]*3 conv_activation = [tf.nn.relu]*3 n_hidden_in = 64 * 11 * 10 # conv3 有 64 個 11x10 映射 each n_hidden = 512 hidden_activation = tf.nn.relu n_outputs = env.action_space.n # 9個離散動作 initializer = tf.contrib.layers.variance_scaling_initializer() def q_network(X_state, scope): prev_layer = X_state conv_layers = [] with tf.variable_scope(scope) as scope: for n_maps, kernel_size, stride, padding, activation in zip(conv_n_maps, conv_kernel_sizes, conv_strides, conv_paddings, conv_activation): prev_layer = convolution2d(prev_layer, num_outputs=n_maps, kernel_size=kernel_size, stride=stride, padding=padding, activation_fn=activation, weights_initializer=initializer) conv_layers.append(prev_layer) last_conv_layer_flat = tf.reshape(prev_layer, shape=[-1, n_hidden_in]) hidden = fully_connected(last_conv_layer_flat, n_hidden, activation_fn=hidden_activation, weights_initializer=initializer) outputs = fully_connected(hidden, n_outputs, activation_fn=None, weights_initializer=initializer) trainable_vars = tf.get_collection(tf.GraphKeys.TRAINABLE_VARIABLES, scope=scope.name) trainable_vars_by_name = {var.name[len(scope.name):]: var for var in trainable_vars} return outputs, trainable_vars_by_name ``` 該代碼的第一部分定義了DQN體系結構的超參數。然后`q_network()`函數創建 DQN，將環境的狀態`X_state`作為輸入，以及變量范圍的名稱。請注意，我們將只使用一個觀察來表示環境的狀態，因為幾乎沒有隱藏的狀態（除了閃爍的物體和鬼魂的方向）。 `trainable_vars_by_name`字典收集了所有 DQN 的可訓練變量。當我們創建操作以將評論家 DQN 復制到行動者 DQN 時，這將是有用的。字典的鍵是變量的名稱，去掉與范圍名稱相對應的前綴的一部分。看起來像這樣： ```python >>> trainable_vars_by_name {'/Conv/biases:0': <tensorflow.python.ops.variables.Variable at 0x121cf7b50>, '/Conv/weights:0': <tensorflow.python.ops.variables.Variable...>, '/Conv_1/biases:0': <tensorflow.python.ops.variables.Variable...>, '/Conv_1/weights:0': <tensorflow.python.ops.variables.Variable...>, '/Conv_2/biases:0': <tensorflow.python.ops.variables.Variable...>, '/Conv_2/weights:0': <tensorflow.python.ops.variables.Variable...>, '/fully_connected/biases:0': <tensorflow.python.ops.variables.Variable...>, '/fully_connected/weights:0': <tensorflow.python.ops.variables.Variable...>, '/fully_connected_1/biases:0': <tensorflow.python.ops.variables.Variable...>, '/fully_connected_1/weights:0': <tensorflow.python.ops.variables.Variable...>} ``` 現在讓我們為兩個 DQN 創建輸入占位符，以及復制評論家 DQN 給行動者 DQN 的操作： ```python X_state = tf.placeholder(tf.float32, shape=[None, input_height, input_width,input_channels]) actor_q_values, actor_vars = q_network(X_state, scope="q_networks/actor") critic_q_values, critic_vars = q_network(X_state, scope="q_networks/critic") copy_ops = [actor_var.assign(critic_vars[var_name]) for var_name, actor_var in actor_vars.items()] copy_critic_to_actor = tf.group(*copy_ops) ``` 讓我們后退一步：我們現在有兩個 DQN，它們都能夠將環境狀態（即預處理觀察）作為輸入，并輸出在該狀態下的每一個可能的動作的估計 Q 值。另外，我們有一個名為`copy_critic_to_actor`的操作，將評論家 DQN 的所有可訓練變量復制到行動者 DQN。我們使用 TensorFlow 的`tf.group()`函數將所有賦值操作分組到一個方便的操作中。 行動者 DQN 可以用來扮演 Ms.Pac-Man（最初非常糟糕）。正如前面所討論的，你希望它足夠深入地探究游戲，所以通常情況下你想將它用 ε 貪婪策略或另一種探索策略相結合。 但是評論家 DQN 呢？它如何去學習玩游戲？簡而言之，它將試圖使其預測的 Q 值去匹配行動者通過其經驗的游戲估計的 Q 值。具體來說，我們將讓行動者玩一段時間，把所有的經驗保存在回放記憶存儲器中。每個記憶將是一個 5 元組（狀態、動作、下一狀態、獎勵、繼續），其中“繼續”項在游戲結束時等于 0，否則為 1。接下來，我們定期地從回放存儲器中采樣一批記憶，并且我們將估計這些存儲器中的 Q 值。最后，我們將使用監督學習技術訓練評論家 DQN 去預測這些 Q 值。每隔幾個訓練周期，我們會把評論家 DQN 復制到行動者 DQN。就這樣！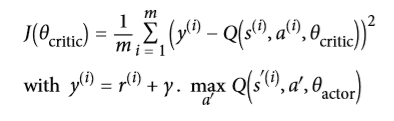公式 16-7 示出了用于訓練評論家 DQN 的損失函數：  其中： + 和分別為狀態，行為，回報，和下一狀態，均從存儲器中第`i`次采樣得到 + `m`是記憶批處理的長度 + θ critic和` θactor `為評論者和行動者的參數 + 是評論家 DQN 對第`i`記憶狀態行為 Q 值的預測 + 是演員 DQN 在選擇動作`A'`時的下一狀態`S'`的期望 Q 值的預測 + `y`是第`i`記憶的目標 Q 值，注意，它等同于行動者實際觀察到的獎勵，再加上行動者對如果它能發揮最佳效果（據它所知），未來的回報應該是什么的預測。 + `J`為訓練評論家 DQN 的損失函數。正如你所看到的，這只是由行動者 DQN 估計的目標 Q 值`y`和評論家 DQN 對這些 Q 值的預測之間的均方誤差。 回放記憶是可選的，但強烈推薦使它存在。沒有它，你會訓練評論家 DQN 使用連續的經驗，這可能是相關的。這將引入大量的偏差并且減慢訓練算法的收斂性。通過使用回放記憶，我們確保饋送到訓練算法的存儲器可以是不相關的。 讓我們添加評論家 DQN 的訓練操作。首先，我們需要能夠計算其在存儲器批處理中的每個狀態動作的預測 Q 值。由于 DQN 為每一個可能的動作輸出一個 Q 值，所以我們只需要保持與在該存儲器中實際選擇的動作相對應的 Q 值。為此，我們將把動作轉換成一個熱向量（記住這是一個滿是 0 的向量，除了第`i`個索引中的1），并乘以 Q 值：這將刪除所有與記憶動作對應的 Q 值外的 Q 值。然后只對第一軸求和，以獲得每個存儲器所需的 Q 值預測。 ```python X_action = tf.placeholder(tf.int32, shape=[None]) q_value = tf.reduce_sum(critic_q_values * tf.one_hot(X_action, n_outputs), axis=1, keep_dims=True) ``` 接下來，讓我們添加訓練操作，假設目標Q值將通過占位符饋入。我們還創建了一個不可訓練的變量`global_step`。優化器的`minimize()`操作將負責增加它。另外，我們創建了`init`操作和`Saver`。 ```python y = tf.placeholder(tf.float32, shape=[None, 1]) cost = tf.reduce_mean(tf.square(y - q_value)) global_step = tf.Variable(0, trainable=False, name='global_step') optimizer = tf.train.AdamOptimizer(learning_rate) training_op = optimizer.minimize(cost, global_step=global_step) init = tf.global_variables_initializer() saver = tf.train.Saver() ``` 這就是訓練階段的情況。在我們查看執行階段之前，我們需要一些工具。首先，讓我們從回放記憶開始。我們將使用一個`deque`列表，因為在將數據推送到隊列中并在達到最大內存大小時從列表的末尾彈出它們使是非常有效的。我們還將編寫一個小函數來隨機地從回放記憶中采樣一批處理： ```python from collections import deque replay_memory_size = 10000 replay_memory = deque([], maxlen=replay_memory_size) def sample_memories(batch_size): indices = rnd.permutation(len(replay_memory))[:batch_size] cols = [[], [], [], [], []] # state, action, reward, next_state, continue for idx in indices: memory = replay_memory[idx] for col, value in zip(cols, memory): col.append(value) cols = [np.array(col) for col in cols] return (cols[0], cols[1], cols[2].reshape(-1, 1), cols[3],cols[4].reshape(-1, 1)) ``` 接下來，我們需要行動者來探索游戲。我們使用 ε 貪婪策略，并在 50000 個訓練步驟中逐步將`ε`從 1 降低到 0.05。 ```python eps_min = 0.05 eps_max = 1.0 eps_decay_steps = 50000 def epsilon_greedy(q_values, step): epsilon = max(eps_min, eps_max - (eps_max-eps_min) * step/eps_decay_steps) if rnd.rand() < epsilon: return rnd.randint(n_outputs) # 隨機動作 else: return np.argmax(q_values) # 最優動作 ``` 就是這樣！我們準備好開始訓練了。執行階段不包含太復雜的東西，但它有點長，所以深呼吸。準備好了嗎？來次夠！首先，讓我們初始化幾個變量： ```python n_steps = 100000 # 總的訓練步長 training_start = 1000 # 在游戲1000次迭代后開始訓練 training_interval = 3 # 每3次迭代訓練一次 save_steps = 50 # 每50訓練步長保存模型 copy_steps = 25 # 每25訓練步長后復制評論家Q值到行動者 discount_rate = 0.95 skip_start = 90 # 跳過游戲開始(只是等待時間) batch_size = 50 iteration = 0 # 游戲迭代 checkpoint_path = "./my_dqn.ckpt" done = True # env 需要被重置 ``` 接下來，讓我們打開會話并開始訓練： ```python with tf.Session() as sess: if os.path.isfile(checkpoint_path): saver.restore(sess, checkpoint_path) else: init.run() while True: step = global_step.eval() if step >= n_steps: break iteration += 1 if done: # 游戲結束，重來 obs = env.reset() for skip in range(skip_start): # 跳過游戲開頭 obs, reward, done, info = env.step(0) state = preprocess_observation(obs) # 行動者評估要干什么 q_values = actor_q_values.eval(feed_dict={X_state: [state]}) action = epsilon_greedy(q_values, step) # 行動者開始玩游戲 obs, reward, done, info = env.step(action) next_state = preprocess_observation(obs) # 讓我們記下來剛才發生了啥 replay_memory.append((state, action, reward, next_state, 1.0 - done)) state = next_state if iteration < training_start or iteration % training_interval != 0: continue # 評論家學習 X_state_val, X_action_val, rewards, X_next_state_val, continues = ( sample_memories(batch_size)) next_q_values = actor_q_values.eval( feed_dict={X_state: X_next_state_val}) max_next_q_values = np.max(next_q_values, axis=1, keepdims=True) y_val = rewards + continues * discount_rate * max_next_q_values training_op.run(feed_dict={X_state: X_state_val,X_action: X_action_val, y: y_val}) # 復制評論家Q值到行動者 if step % copy_steps == 0: copy_critic_to_actor.run() # 保存模型 if step % save_steps == 0: saver.save(sess, checkpoint_path) ``` 如果檢查點文件存在，我們就開始恢復模型，否則我們只需初始化變量。然后，主循環開始，其中`iteration`計算從程序開始以來游戲步驟的總數，同時`step`計算從訓練開始的訓練步驟的總數（如果恢復了檢查點，也恢復全局步驟）。然后代碼重置游戲（跳過第一個無聊的等待游戲的步驟，這步驟啥都沒有）。接下來，行動者評估該做什么，并且玩游戲，并且它的經驗被存儲在回放記憶中。然后，每隔一段時間（熱身期后），評論家開始一個訓練步驟。它采樣一批回放記憶，并要求行動者估計下一狀態的所有動作的Q值，并應用公式 16-7 來計算目標 Q 值`y_val`.這里唯一棘手的部分是，我們必須將下一個狀態的 Q 值乘以`continues`向量，以將對應于游戲結束的記憶 Q 值清零。接下來，我們進行訓練操作，以提高評論家預測 Q 值的能力。最后，我們定期將評論家的 Q 值復制給行動者，然后保存模型。 不幸的是，訓練過程是非常緩慢的：如果你使用你的破筆記本電腦進行訓練的話，想讓 Ms. Pac-Man 變好一點點你得花好幾天，如果你看看學習曲線，計算一下每次的平均獎勵，你會發現到它是非常嘈雜的。在某些情況下，很長一段時間內可能沒有明顯的進展，直到智能體學會在合理的時間內生存。如前所述，一種解決方案是將盡可能多的先驗知識注入到模型中（例如，通過預處理、獎勵等），也可以嘗試通過首先訓練它來模仿基本策略來引導模型。在任何情況下，RL仍然需要相當多的耐心和調整，但最終結果是非常令人興奮的。 ## 練習 1. 你怎樣去定義強化學習？它與傳統的監督以及非監督學習有什么不同？ 2. 你能想到什么本章沒有提到過的強化學習應用？智能體是什么？什么是可能的動作，什么是獎勵？ 3. 什么是衰減率？如果你修改了衰減率那最優策略會變化嗎？ 4. 你怎么去定義強化學習智能體的表現？ 5. 什么是信用評估問題？它怎么出現的？你怎么解決？ 6. 使用回放記憶的目的是什么？ 7. 什么是閉策略 RL 算法？ 8. 使用深度 Q 學習來處理 OpenAI gym 的“BypedalWalker-v2” 。QNET 不需要對這個任務使用非常深的網絡。 9. 使用策略梯度訓練智能體扮演 Pong，一個著名的 Atari 游戲（PANV0 在 OpenAI gym 的 Pong-v0）。注意：個人的觀察不足以說明球的方向和速度。一種解決方案是一次將兩次觀測傳遞給神經網絡策略。為了減少維度和加速訓練，你必須預先處理這些圖像（裁剪，調整大小，并將它們轉換成黑白），并可能將它們合并成單個圖像（例如去疊加它們）。 10. 如果你有大約 100 美元備用，你可以購買 Raspberry Pi 3 再加上一些便宜的機器人組件，在 PI 上安裝 TensorFlow，然后讓我們嗨起來~！舉個例子，看看 Lukas Biewald 的這個有趣的帖子，或者看看 GoPiGo 或 BrickPi。為什么不嘗試通過使用策略梯度訓練機器人來構建真實的 cartpole ？或者造一個機器人蜘蛛，讓它學會走路；當它接近某個目標時，給予獎勵（你需要傳感器來測量目標的距離）。唯一的限制就是你的想象力。 練習答案均在附錄 A。 ## 感謝 在我們結束這本書的最后一章之前，我想感謝你們讀到最后一段。我真心希望你能像我寫這本書一樣愉快地閱讀這本書，這對你的項目，或多或少都是有用的。 如果發現錯誤，請發送反饋。更一般地說，我很想知道你的想法，所以請不要猶豫，通過 O'Reilly 來與我聯系，或者通過 ageron/handson-ml GITHUB 項目來練習。 對你來說，我最好的建議是練習和練習：如果你還沒有做過這些練習，試著使用 Juyter notebook 參加所有的練習，加入 kaggle 網站或其他 ML 社區，看 ML 課程，閱讀論文，參加會議，會見專家。您可能還想研究我們在本書中沒有涉及的一些主題，包括推薦系統、聚類算法、異常檢測算法和遺傳算法。 我最大的希望是，這本書將激勵你建立一個美妙的 ML 應用程序，這將有利于我們所有人！那會是什么呢？ > 2016 年 11 月 26 日，奧列倫·格倫 > 你的支持，是我們每個開源工作者的驕傲～