# 附錄 D、自動微分
> 譯者:[@rickllyxu](https://github.com/rickllyxu)
這個附錄解釋了 TensorFlow 的自動微分功能是如何工作的,以及它與其他解決方案的對比。
假定你定義了函數 ,需要得到它的偏導數  和 ,以用于梯度下降或者其他優化算法。你的可選方案有手動微分法,符號微分法,數值微分法,前向自動微分,和反向自動微分。TensorFlow 實現的反向自動微分法。我們來看看每種方案。
## 手動微分法
第一個方法是拿起一直筆和一張紙,使用你的代數知識去手動的求偏導數。對于已定義的函數,求它的偏導并不太困難。你需要使用如下 5 條規則:
- 常數的導數為 0。
-  的導數為 , 為常數。
-  的導數是 
- 函數的和的導數,等于函數的導數的和
-  乘以函數,再求導,等于  乘以函數的導數
從上述這些規則,可得到公式 D-1。
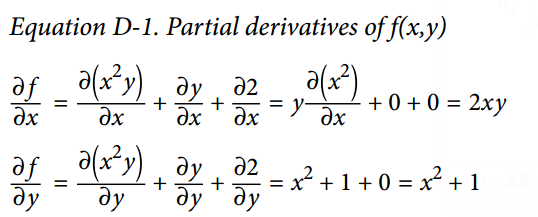
這個種方法應用于更復雜函數時將變得非常羅嗦,并且有可能出錯。好消息是,像剛才我們做的求數學式子的偏導數可以被自動化,通過一個稱為符號微分的過程。
## 符號微分
圖 D-1 展示了符號微分是如何運行在相當簡單的函數上的,。該函數的計算圖如圖的左邊所示。通過符號微分,我們可得到圖的右部分,它代表了 ,相似地也可得到關于`y`的導數。
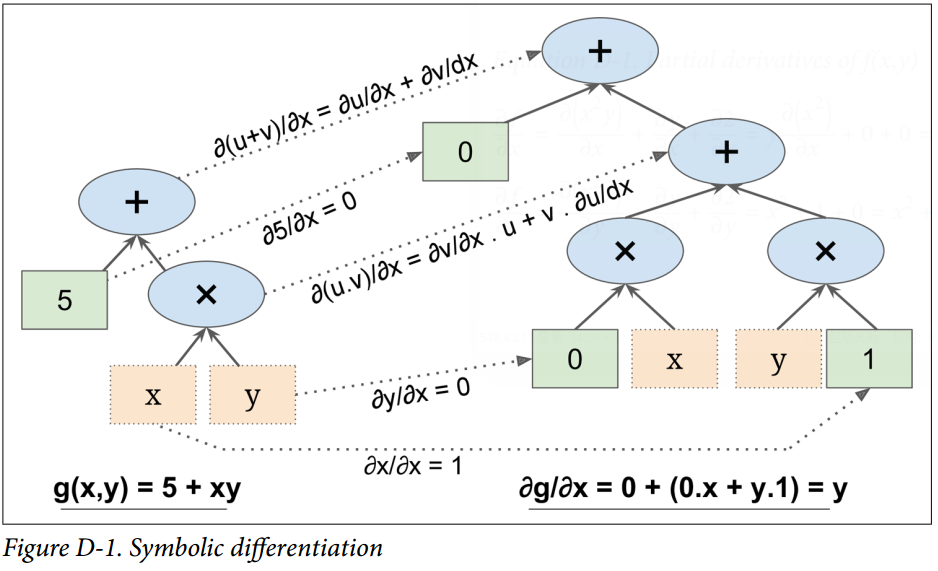
概算法先獲得葉子節點的偏導數。常數 5 返回常數 0,因為常數的導數總是 0。變量`x`返回常數 1,變量`y`返回常數 0,因為 (如果我們找關于`y`的偏導數,那它將反過來)。
現在我們移動到計算圖的相乘節點處,代數告訴我們,`u`和`v`相乘后的導數為 。因此我們可以構造有圖中大的部分,代表`0 × x + y × 1`。
最后我們往上走到計算圖的相加節點處,正如 5 條規則里提到的,和的導數等于導數的和。所以我們只需要創建一個相加節點,連接我們已經計算出來的部分。我們可以得到正確的偏導數,即:。
然而,這個過程可簡化。對該圖應用一些微不足道的剪枝步驟,可以去掉所有不必要的操作,然后我們可以得到一個小得多的只有一個節點的偏導計算圖:。
在這個例子里,簡化操作是相當簡單的,但對更復雜的函數來說,符號微分會產生一個巨大的計算圖,該圖可能很難去簡化,以導致次優的性能。更重要的是,符號微分不能處理由任意代碼定義的函數,例如,如下已在第 9 章討論過的函數:
```python
def my_func(a, b):
z = 0
for i in range(100):
z = a * np.cos(z + i) + z * np.sin(b - i)
return z
```
## 數值微分
從數值上說,最簡單的方案是去計算導數的近似值。回憶`h(x)`在  的導數 ,是該函數在該點處的斜率,或者更準確如公式 D-2 所示。

因此如果我們想要計算  關于`x`,在  處的導數,我們可以簡單計算  的值,將這個結果除以 ,且  去很小的值。這個過程正是如下的代碼所要干的。
```python
def f(x, y):
return x**2*y + y + 2
def derivative(f, x, y, x_eps, y_eps):
return (f(x + x_eps, y + y_eps) - f(x, y)) / (x_eps + y_eps)
df_dx = derivative(f, 3, 4, 0.00001, 0)
df_dy = derivative(f, 3, 4, 0, 0.00001)
```
不幸的是,偏導的結果并不準確(并且可能在求解復雜函數時更糟糕)。上述正確答案分別是 24 和 10 ,但我們得到的是:
```python
>>> print(df_dx)
24.000039999805264
>>> print(df_dy)
10.000000000331966
```
注意到為了計算兩個偏導數, 我們不得不調用`f()`至少三次(在上述代碼里我們調用了四次,但可以優化)。如果存在 1000 個參數,我們將會調用`f()`至少 1001 次。當處理大的神經網絡時,這樣的操作很沒有效率。
然而,數值微分實現起來如此簡單,以至于它是檢查其他方法正確性的優秀工具。例如,如果它的結果與您手動計算的導數不同,那么你的導數可能包含錯誤。
## 前向自動微分
前向自動微分既不是數值微分,也不是符號微分,但在某些方面,它是他們的愛情結晶。它依賴對偶數。對偶數是奇怪但迷人的,是  形式的數,這里`a`和`b`是實數, 是無窮小的數,滿足 ,但 。你可以認為對偶數  類似于有著無窮個 0 的 42.0000?000024(但當然這是簡化后的,僅僅給你對偶數什么的想法)。一個對偶數在內存中表示為一個浮點數對,例如, 表示為`(42.0, 24.0)`。
對偶數可相加、相乘、等等操作,正如公式 D-3 所示。
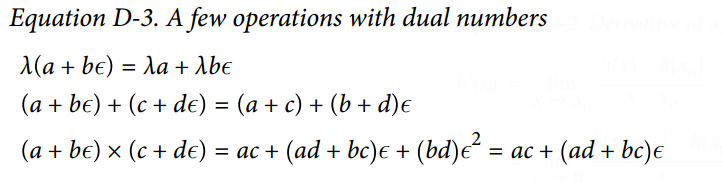
最重要的,可證明`h(a + b?) = h(a) + b × h'(a)?`,所以計算一次`h(a + ?)`就得到了兩個值`h(a)`和`h'(a)`。圖 D-2 展示了前向自動微分如何計算  關于`x`,在  處的導數。我們所要做的一切只是計算 ;它將輸出一個對偶數,其第一部分等于 ,第二部分等于 。
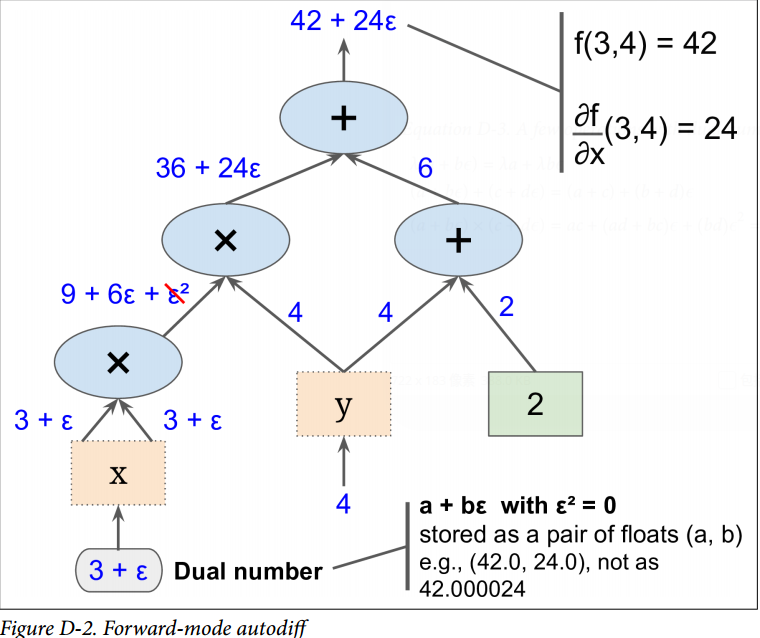
為了計算  我們不得不再遍歷一遍計算圖,但這次前饋的值為 。
所以前向自動微分比數值微分準確得多,但它遭受同樣的缺陷:如果有 1000 個參數,那為了計算所有的偏導數,得歷經計算圖 1000 次。這正是反向自動微分耀眼的地方:計算所有的偏導數,它只需要遍歷計算圖 2 次。
## 反向自動微分
反向自動微分是 TensorFlow 采取的方案。它首先前饋遍歷計算圖(即,從輸入到輸出),計算出每個節點的值。然后進行第二次遍歷,這次是反向遍歷(即,從輸出到輸入),計算出所有的偏導數。圖 D-3 展示了第二次遍歷的過程。在第一次遍歷過程中,所有節點值已被計算,輸入是 。你可以在每個節點底部右方看到這些值(例如,)。節點已被標號,從 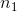 到 。輸出節點是 。
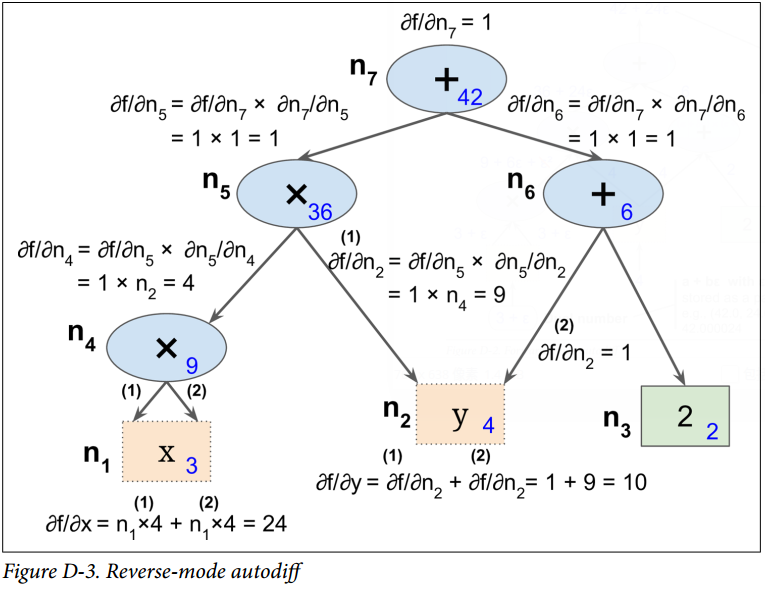
這個計算關于每個連續節點的偏導數的思想逐漸地從上到下遍歷圖,直到到達變量節點。為實現這個,反向自動微分強烈依賴于鏈式法則,如公式 D-4 所示。
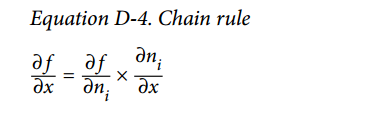
由于  是輸出節點,即 ,所以 。
接著到了圖的  節點:當  變化時, 會變化多少?答案是 。我們已經知道 ,因此我們只需要知道  就行。因為  是  的和,因此可得到 ,因此 。
現在前進到 :當  變化時, 會變化多少?答案是 。由于 ,我們可得到 ,所以 。
這個遍歷過程一直持續,此時我們達到圖的底部。這時我們已經得到了所有偏導數在點  處的值。在這個例子里,我們得到 。聽起來很美妙!
反向自動微分是非常強大且準確的技術,尤其是當有很多輸入參數和極少輸出時,因為它只要求一次前饋傳遞加上一次反向傳遞,就可計算所有輸出關于所有輸入的偏導數。最重要的是,它可以處理任意代碼定義的函數。它也可以處理那些不完全可微的函數,只要 你要求他計算的偏導數在該點處是可微的。
如果你在 TensorFlow 中實現了新算子,你想使它與現有的自動微分相兼容,那你需要提供函數,該函數用于構建一個子圖,來計算關于新算子輸入的偏導數。例如,假設你實現了一個計算其輸入的平方的函數,平方算子 ,在這個例子中你需要提供相應的導函數 。注意這個導函數不計算一個數值結果,而是用于構建子圖,該子圖后續將計算偏導結果。這是非常有用的,因為這意味著你可以計算梯度的梯度(為了計算二階導數,或者甚至更高階的導數)。
