# 二、圖 > 原文：[Chapter 2 Graphs](http://greenteapress.com/complexity2/html/thinkcomplexity2003.html) > 譯者：[飛龍](https://github.com/wizardforcel) > 協議：[CC BY-NC-SA 4.0](http://creativecommons.org/licenses/by-nc-sa/4.0/) > 自豪地采用[谷歌翻譯](https://translate.google.cn/) 本書的前三章有關一些模型，它們描述了由組件和組件之間的連接組成的系統。例如，在生態食物網中，組件是物種，連接代表捕食者和獵物的關系。 在本章中，我介紹了 NetworkX，一個用于構建和研究這些模型的 Python 包。我們從 Erd?s-Rényi 模型開始，它具有一些有趣的數學屬性。在下一章中，我們將介紹更有用的，解釋現實系統的模型。 本章的代碼在本書倉庫中的`chap02.ipynb`中。使用代碼的更多信息請參見第（？）章。 ## 2.1 圖是什么？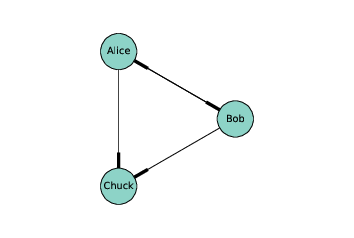  > 圖 2.1：表示社交網絡的有向圖 對于大多數人來說，圖是數據集的視覺表示，如條形圖或股票價格對于時間的繪圖。這不是本章的內容。 在本章中，圖是一個系統的表示，它包含離散的互連元素。元素由節點表示，互連由邊表示。 例如，你可以表示一個路線圖，每個城市都是一個節點，每個城市之間的路線是一條邊。或者你可以表示一個社交網絡，每個人是節點，如果他們是朋友，兩個人之間有邊，否則沒有。 在某些圖中，邊具有長度，成本或權重等屬性。例如，在路線圖中，邊的長度可能代表兩個城市之間的距離，或旅行時間。在社交網絡中，可能會有不同的邊來表示不同種類的關系：朋友，商業伙伴等。 邊可以是有向或無向的，這取決于它們表示的關系是不對稱的還是對稱的。在路線圖中，你可能會使用有向邊表示單向街道，使用無向邊表示雙向街道。在某些社交網絡，如 Facebook，好友是對稱的：如果 A 是 B 的朋友，那么 B 也是 A 的朋友。但在 Twitter 上，“關注”關系并不對稱；如果 A 關注了 B，這并不意味著 B 關注 A。因此，你可以使用無向邊來表示 Facebook 網絡，并將有向邊用于 Twitter。 圖具有有趣的數學屬性，并且有一個稱為圖論的數學分支，用于研究它們。 圖也很有用，因為有許多現實世界的問題可以使用圖的算法來解決。例如，Dijkstra 的最短路徑算法，是從圖中找到某個節點到所有其他節點的最短路徑的有效方式。路徑是兩個節點之間的，帶有邊的節點序列。 圖的節點通常以圓形或方形繪制，邊通常以直線繪制。例如，上面的有向圖中，節點可能代表在 Twitter 上彼此“關注”的三個人。線的較厚部分表示邊的方向。在這個例子中，愛麗絲和鮑勃相互關注，都關注查克，但查克沒有關注任何人。 下面的無向圖展示了美國東北部的四個城市；邊上的標簽表示駕駛時間，以小時為單位。在這個例子中，節點的位置大致對應于城市的地理位置，但是通常圖的布局是任意的。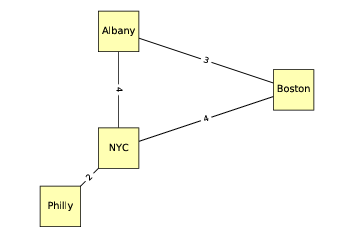 ## 2.2 NetworkX  > 圖 2.2：表示城市和高速公路的無向圖 為了表示圖，我們將使用一個名為 NetworkX 的包，它是 Python 中最常用的網絡庫。你可以在 <https://networkx.github.io/> 上閱讀更多信息，但是我們之后會解釋。 我們可以通過導入 NetworkX 和實例化`nx.DiGraph`來創建有向圖： ```py import networkx as nx G = nx.DiGraph() ``` 通常將 NetworkX 導入為`nx`。此時，`G`是一個`DiGraph`對象，不包含節點和邊。我們可以使用`add_node`方法添加節點： ```py G.add_node('Alice') G.add_node('Bob') G.add_node('Chuck') ``` 現在我們可以使用`nodes`方法獲取節點列表： ```py >>> G.nodes() ['Alice', 'Bob', 'Chuck'] ``` 添加邊的方式幾乎相同： ```py G.add_edge('Alice', 'Bob') G.add_edge('Alice', 'Chuck') G.add_edge('Bob', 'Alice') G.add_edge('Bob', 'Chuck') ``` 我們可以使用`edges`來獲取邊的列表： ```py >>> G.edges() [('Alice', 'Bob'), ('Alice', 'Chuck'), ('Bob', 'Alice'), ('Bob', 'Chuck')] ``` NetworkX 提供了幾個繪圖的功能；`draw_circular`將節點排列成一個圓，并使用邊將它們連接： ```py nx.draw_circular(G, node_color=COLORS[0], node_size=2000, with_labels=True) ``` 這就是我用來生成圖（？）的代碼。`with_labels`選項標注了節點；在下一個例子中，我們將看到如何標注邊。 為了產生圖（？），我們以一個字典開始，它將每個城市的名稱，映射為對應的經緯度： ```py pos = dict(Albany=(-74, 43), Boston=(-71, 42), NYC=(-74, 41), Philly=(-75, 40)) ``` 因為這是個無向圖，我實例化了`nx.Graph`： ```py G = nx.Graph() ``` 之后我可以使用`add_nodes_from`來迭代`pos`的鍵，并將它們添加為節點。 ```py G.add_nodes_from(pos) ``` 下面我會創建一個字典，將每條邊映射為對應的駕駛時間。 ```py drive_times = {('Albany', 'Boston'): 3, ('Albany', 'NYC'): 4, ('Boston', 'NYC'): 4, ('NYC', 'Philly'): 2} ``` 現在我可以使用`add_edges_from`，它迭代了`drive_times`的鍵，并將它們添加為邊： ```py G.add_edges_from(drive_times) ``` 現在我不使用`draw_circular`，它將節點排列成一個圓圈，而是使用`draw`，它接受`pos`作為第二個參數： ```py nx.draw(G, pos, node_color=COLORS[1], node_shape='s', node_size=2500, with_labels=True) ``` `pos`是一個字典，將每個城市映射為其坐標；`draw`使用它來確定節點的位置。 要添加邊的標簽，我們使用`draw_networkx_edge_labels`： ```py nx.draw_networkx_edge_labels(G, pos, edge_labels=drive_times) ``` `drive_times`是一個字典，將每條邊映射為它們之間的駕駛距離，每條邊表示為城市名稱的偶對。這就是我生成圖（？）的方式。 在這兩個例子中，這些節點是字符串，但是通常它們可以是任何可哈希的類型。 ## 2.3 隨機圖 隨機圖就像它的名字一樣：一個隨機生成的節點和邊的圖。當然，有許多隨機過程可以生成圖，所以有許多種類的隨機圖。 其中一個更有趣的是 Erd?s-Rényi 模型，PaulErd?s 和 AlfrédRényi 在 20 世紀 60 年代研究過它。 Erd?s-Rényi 圖（ER 圖）的特征在于兩個參數：`n`是節點的數量，`p`是任何兩個節點之間存在邊的概率。見 <http://en.wikipedia.org/wiki/Erdos-Renyi_model>。 Erd?s 和 Rényi 研究了這些隨機圖的屬性；其令人驚奇的結果之一就是，隨著隨機的邊被添加，隨機圖的屬性會突然變化。 展示這類轉變的一個屬性是連通性。如果每個節點到每個其他節點都存在路徑，那么無向圖是連通的。 在 ER 圖中，當`p`較小時，圖是連通圖的概率非常低，而`p`較大時接近`1`。在這兩種狀態之間，在`p`的特定值處存在快速轉變，表示為`p*`。 Erd?s 和 Rényi 表明，這個臨界值是`p* = lnn / n`，其中`n`是節點數。如果`p < p*`，隨機圖`G(n, p)`不太可能連通，并且如果`p > p*`，則很可能連通。 為了測試這個說法，我們將開發算法來生成隨機圖，并檢查它們是否連通。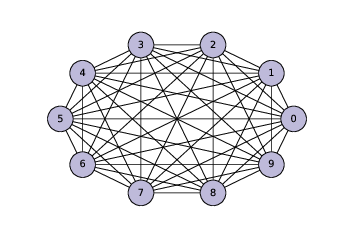 ## 2.4 生成圖  我將首先生成一個完全圖，這是一個圖，其中每個節點都彼此連接。 這是一個生成器函數，它接收節點列表并枚舉所有不同的偶對。如果你不熟悉生成器函數，你可能需要閱讀附錄？，然后回來。 ```py def all_pairs(nodes): for i, u in enumerate(nodes): for j, v in enumerate(nodes): if i>j: yield u, v ``` 你可以使用`all_pairs`來構造一個完全圖。 ```py def make_complete_graph(n): G = nx.Graph() nodes = range(n) G.add_nodes_from(nodes) G.add_edges_from(all_pairs(nodes)) return G ``` `make_complete_graph`接受節點數`n`，并返回一個新的`Graph`，擁有`n`個節點，所有節點之間都有邊。 以下代碼生成了一個包含 10 個節點的完全圖，并繪制出來。 ```py complete = make_complete_graph(10) nx.draw_circular(complete, node_color=COLORS[2], node_size=1000, with_labels=True) ``` 圖（？）顯示了結果。不久之后，我們將修改此代碼來生成 ER 圖，但首先我們將開發函數來檢查圖是否是連通的。 ## 2.5 連通圖 如果每個節點到每個其他節點都存在路徑，這個圖就是連通圖。請見<http://en.wikipedia.org/wiki/Connectivity_(graph_theory)>。 對于許多涉及圖的應用，檢查圖是否連通是很有用的。幸運的是，有一個簡單的算法。 你可以從任何節點起步，并檢查是否可以到達所有其他節點。如果你可以到達一個節點`v`，你可以到達`v`的任何一個鄰居，他們是`v`通過邊連接的任何節點。 `Graph`類提供了一個稱為`neighbors`的方法，返回給定節點的鄰居列表。例如，在上一節中我們生成的完全圖中： ```py >>> complete.neighbors(0) [1, 2, 3, 4, 5, 6, 7, 8, 9] ``` 假設我們從節點`s`起步。我們可以將`s`標記為“已訪問”，然后我們可以標記它的鄰居。然后我們標記鄰居的鄰居，依此類推，直到你無法再到達任何節點。如果訪問了所有節點，則圖是連通圖。 以下是 Python 中的樣子： ```py def reachable_nodes(G, start): seen = set() stack = [start] while stack: node = stack.pop() if node not in seen: seen.add(node) stack.extend(G.neighbors(node)) return seen ``` `reachable_nodes`接受`Graph`和起始節點`start`，并返回可以從`start`到達的節點集合，他們。 最初，已訪問的集合是空的，我們創建一個名為`stack`的列表，跟蹤我們發現但尚未處理的節點。最開始，棧包含單個節點`start`。 現在，每次在循環中，我們： + 從棧中刪除一個節點。 + 如果節點已在`seen`中，我們返回到步驟 1。 + 否則，我們將節點添加到`seen`，并將其鄰居添加到棧。 當棧為空時，我們無法再到達任何節點，所以我們終止了循環并返回。 例如，我們可以找到從節點`0`可到達的，完全圖中的所有節點： ```py >>> reachable_nodes(complete, 0) {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} ``` 最初，棧包含節點`0`，`seen`是空的。第一次循環中，節點`0`添加到了`seen`，所有其他節點添加到了棧中（因為它們都是節點`0`的鄰居）。 下一次循環中，`pop`返回棧中的最后一個元素，即節點`9.`因此，節點`9`被添加到`seen`，并且其鄰居被添加到棧。 請注意，同一個節點在棧中可能會出現多次；實際上，具有`k`個鄰居的節點將添加到棧`k`次。稍后我們將尋找方法，來使此算法更有效率。 我們可以使用`reachable_nodes`來編寫`is_connected`： ```py def is_connected(G): start = next(G.nodes_iter()) reachable = reachable_nodes(G, start) return len(reachable) == len(G) ``` `is_connected`通過調用`nodes_iter`來選擇一個起始節點，`node_iter`返回一個迭代器對象，并將結果傳遞給`next`，返回第一個節點。 `reachable`獲取了一組節點，它們可以從`start`到達。如果這個集合的大小與圖的大小相同，那意味著我們可以訪問所有節點，也就是這個圖是連通的。 一個完全圖是連通的，毫不奇怪： ```py >>> is_connected(complete) True ``` 下一節中，我們會生成 ER 圖，并檢查它們是否是連通的。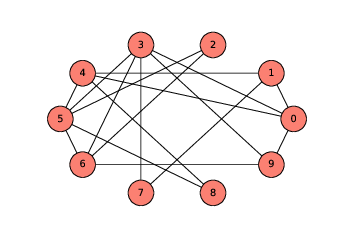 ## 2.6 生成 ER圖  > 圖 2.4：ER 圖，`n=10`，`p=0.3` ER 圖`G(n, p) `包含`n`個節點，每對節點以概率為`p`的邊連接。生成 ER 圖類似于生成完全圖。 以下生成器函數枚舉所有可能的邊，并使用輔助函數`flip`，來選擇哪些應添加到圖中： ```py def random_pairs(nodes, p): for i, u in enumerate(nodes): for j, v in enumerate(nodes): if i>j and flip(p): yield u, v ``` `flip`以給定概率`p`返回`True`，以互補的概率`1-p`返回`False`。 ```py from numpy.random import random def flip(p): return random() < p ``` 最后，`make_random_graph`生成并返回 ER 圖`G(n, p)`。 ```py def make_random_graph(n, p): G = nx.Graph() nodes = range(n) G.add_nodes_from(nodes) G.add_edges_from(random_pairs(nodes, p)) return G ``` `make_random_graph`幾乎和`make_complete_graph`，唯一的不同是它使用`random_pairs`而不是`all_pairs`。 這里是`p=0.3`的例子： ```py random_graph = make_random_graph(10, 0.3) ``` 圖（？）展示了結果。這個圖是連通圖；事實上，大多數`p=10`并且`p=3`的 ER 圖都是連通圖。在下一節中，我們將看看有多少。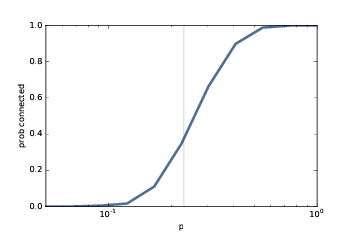 ## 2.7 連通性的概率  > 圖 2.5：連通性的概率，`n=10`，`p`是一個范圍。豎直的線展示了預測的臨界值。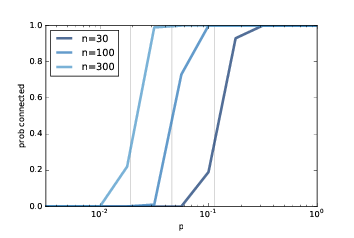  >圖 2.6：連通性的概率，`n`是多個值，`p`是一個范圍。 對于`n`和`p`的給定值，我們想知道`G(n, p)`連通的概率。我們可以通過生成大量隨機圖，來計算有多少個來估計它。就是這樣： ```py def prob_connected(n, p, iters=100): count = 0 for i in range(iters): random_graph = make_random_graph(n, p) if is_connected(random_graph): count += 1 return count/iters ``` `iters`是我們生成的隨機圖的數量。隨著我們增加`iter`，估計的概率就會更加準確。 ```py >>> prob_connected(10, 0.3, iters=10000) 0.6454 ``` 在具有這些參數的 10000 個 ER 圖中，6498 個是連通的，因此我們估計其中65％是連通的。所以 0.3 接近臨界值，在這里連通概率從接近 0 變為接近 1。根據 Erd?s 和 Rényi，`p* = lnn / n = 0.23`。 我們可以通過估計一系列`p`值的連通概率，來更清楚地了解轉變： ```py import numpy as np n = 10 ps = np.logspace(-2.5, 0, 11) ys = [prob_connected(n, p) for p in ps] ``` 這是我們看到的使用 NumPy 的第一個例子。按照慣例，我將 NumPy 導入為`np`。函數`logspace`返回從`10 ** -2.5`到`10 ** 0 = 1`的 11 個元素的數組，在對數刻度上等間隔。 為了計算`y`，我使用列表推導來迭代`ps`的元素，并計算出每個值為`p`的隨機圖的連通概率。 圖（？）展示了結果，豎直的線為`p*`。從 0 到 1 的轉變發生在預測的臨界值附近。在對數刻度上，這個轉變大致對稱。 對于較大的`n`值，圖（？）展示了類似的結果。隨著`n`的增加，臨界值越來越小，轉變越來越突然。 這些實驗與 Erd?s 和 Rényi 在其論文中證明的結果一致。 ## 2.8 圖的算法分析 這一章中，我提出了一個檢查圖是否連通的算法；在接下來的幾章中，我們將再次看到更多的圖的算法。并且我們要分析這些算法的性能，了解它們的運行時間如何隨著圖大小的增加而增長。 如果你還不熟悉算法分析，在你繼續之前，你應該閱讀附錄一。 圖算法的增長級別通常表示為頂點數量`n`，以及邊數量`m`的函數。 作為一個例子，我們分析從前面的`reachable_nodes`： ```py def reachable_nodes(G, start): seen = set() stack = [start] while stack: node = stack.pop() if node not in seen: seen.add(node) stack.extend(G.neighbors(node)) return seen ``` 每次循環，我們從棧中彈出一個節點；默認情況下，`pop`刪除并返回列表的最后一個元素，這是一個常數時間的操作。 接下來我們檢查節點是否被已訪問，這是一個集合，所以檢查成員是常數時間。 如果節點還沒有訪問，我們添加它是常量時間，然后將鄰居添加到棧中，這相對于鄰居數量是線性的。 為了使用`n`和`m`表達運行時間，我們可以將每個節點添加到`seen`和`stack`的總次數加起來。 每個節點只添加一次，所以添加的總數為`n`。 但是節點可能多次被添加到棧，具體取決于它們有多少鄰居。如果節點具有`k`個鄰居，則它會被添加到棧`k`次。當然，如果它有`k`個鄰居，那意味著它擁有`k`個邊。 所以添加到棧的總數是邊的數量`m`的兩倍，由于我們考慮每個邊兩次。 因此，這個函數的增長級別為`O(n + m)`，我們可以說，即運行時間與`n`或`m`成正比，以較大者為準。 如果我們知道`n`和`m`之間的關系，我們可以簡化這個表達式。例如，在完全圖中，邊數是`n(n-1)/ 2`，它屬于`O(n^2)`。所以對于一個完全圖，`reachable_nodes`是二次于`n`的。 ## 2.9 練習 本章的代碼在`chap02.ipynb`中，它是本書的倉庫中的 Jupyter 筆記本。使用此代碼的更多信息，請參閱第（？）節。 練習 1：啟動`chap02.ipynb`并運行代碼。筆記本中嵌入了一些簡單的練習，你可能想嘗試一下。 練習 2：我們分析了`reachable_nodes`的性能，并將其分類為`O(n + m)`，其中`n`是節點數，`m`是邊數。繼續分析，`is_connected`的增長級別是什么？ ```py def is_connected(G): start = next(G.nodes_iter()) reachable = reachable_nodes(G, start) return len(reachable) == len(G) ``` 練習 3 ：在我實現`reachable_nodes`時，你可能很困惑，因為向棧中添加所有鄰居而不檢查它們是否已訪問，明顯是低效的。編寫一個該函數的版本，在將鄰居添加到棧之前檢查它們。這個“優化”是否改變了增長級別？它是否使函數更快？ > 譯者注：在彈出節點時將其添加到`seen`，在遍歷鄰居時檢查它們是否已訪問。 練習 4： 實際上有兩種 ER 圖。我們在本章中生成的一種，`G(n，p)`的特征是兩個參數，節點數量和節點之間的邊的概率。 一種替代定義表示為`G(n，m)`，也以兩個參數為特征：節點數`n`和邊數`m`。在這個定義中，邊數是固定的，但它們的位置是隨機的。 使用這個替代定義，重復這一章的實驗。這里是幾個如何處理它的建議： 1. 編寫一個名為`m_pairs`的函數，該函數接受節點列表和邊數`m`，并返回隨機選擇的`m`個邊。一個簡單的方法是，生成所有可能的邊的列表，并使用`random.sample`。 2. 編寫一個名為`make_m_graph`的函數，接受`n`和`m`，并返回`n`個節點和`m`個邊的隨機圖。 3. 創建一個`prob_connected`的版本，使用`make_m_graph`而不是`make_random_graph`。 4. 計算一系列`m`值的連通概率。 與第一類 ER 圖的結果相比，該實驗的結果如何？