# 八、自組織臨界 > 原文：[Chapter 8 Self-organized criticality](http://greenteapress.com/complexity2/html/thinkcomplexity2009.html) > 譯者：[飛龍](https://github.com/wizardforcel) > 協議：[CC BY-NC-SA 4.0](http://creativecommons.org/licenses/by-nc-sa/4.0/) > 自豪地采用[谷歌翻譯](https://translate.google.cn/) 在前一章中，我們看到了一個具有臨界點的系統的例子，并且我們探索了臨界系統 - 分形幾何的一個共同特性。 在本章中，我們將探討臨界系統的另外兩個性質：重尾分布，我們在第五章中見過，和粉紅噪聲，我將在本章中解釋。 這些性質是部分有趣的，因為它們在自然界中經常出現；也就是說，許多自然系統會產生分形幾何，重尾分布和粉紅噪聲。 這個觀察提出了一個自然的問題：為什么許多自然系統具有臨界系統的特性？一個可能的答案是自組織臨界性（SOC），這是一些系統向臨界狀態演化并保持它的趨勢。 在本章中，我將介紹沙堆模型，這是第一個展示 SOC 的系統。 本章的代碼位于本書倉庫的`chap08.ipynb`中。使用代碼的更多信息，請參見第？章。 ## 8.1 臨界系統 許多臨界系統表現出常見的行為： + 分形幾何：例如，冷凍的水傾向于形成分形圖案，包括雪花和其他晶體結構。分形的特點是自相似性；也就是說，圖案的一部分與整體的縮放副本相似。 + 一些物理量的重尾分布：例如，在冷凍的水中，晶體尺寸的分布是冪律的。 + 呈現粉紅噪聲的時間變化。復合信號可以分解為它們的頻率分量。在粉紅噪聲中，低頻分量比高頻分量功率更大。具體而言，頻率`f`處的功率與`1 / f`成正比。 臨界系統通常不穩定。例如，為了使水保持部分冷凍狀態，需要主動控制溫度。如果系統接近臨界溫度，則小型偏差傾向于將系統從一個相位移到另一個相位。 許多自然系統表現出典型的臨界性行為，但如果臨界點不穩定，它們本質上不應該是常見的。這是 Bak，Tang 和 Wiesenfeld 的解決的困惑。他們的解決方案稱為自組織臨界（SOC），其中“自組織”意味著從任何初始狀態開始，系統都會轉向臨界狀態，并停留在那里，無需外部控制。 ## 8.2 沙堆 沙堆模型由 Bak，Tang 和 Wiesenfeld 于 1987 年提出。它不是一個現實的沙堆模型，而是一個抽象，它用（1）大量（2）與鄰居互動的元素來模擬物理系統。 沙堆模型是一個二維細胞自動機，每個細胞的狀態代表沙堆的部分斜率。在每個時間步驟中，檢查每個細胞來查看它是否超過臨界值`K`，通常是 3。如果是，則它會“倒塌”并將沙子轉移到四個相鄰細胞；也就是說，細胞的斜率減少 4，并且每個鄰居增加 1。在網格的周邊，所有細胞保持為斜率 0，所以多余的會溢出邊緣。 Bak，Tang 和 Wiesenfeld 首先將所有細胞初始化為大于`K`的水平，然后運行模型直至穩定。然后他們觀察微小擾動的影響；他們隨機選擇一個細胞，將其值增加 1，然后再次運行模型，直至穩定。 對于每個擾動，他們測量`T`，這是沙堆穩定所需的時間步數，`S`是倒塌的細胞總數 [1]。 > [1] 原始論文使用了`S`的不同定義，但是后來的工作使用了這個定義。 大多數情況下，放置一粒沙子不會導致細胞倒塌，因此`T = 1`和`S = 0`。 但偶爾一粒沙子會引起雪崩，影響很大一部分網格。 結果表明，`T`和`S`的分布是重尾的，這支持了系統處于臨界狀態的斷言。 他們得出結論：沙堆模型表現出“自組織臨界性”，這意味著從最初的狀態開始，它不需要外部控制，或者稱之為“微調”任何參數，就可以向臨界狀態發展。 隨著更多沙粒的添加，模型仍處于臨界狀態。 在接下來的幾節中，我復制他們的實驗并解釋結果。 ## 8.3 實現沙堆 為了實現沙堆模型，我定義了一個名為`SandPile`的類，該類繼承自`Cell2D.py`中定義的`Cell2D`。 ```py class SandPile(Cell2D): def __init__(self, n, m, level=9): self.array = np.ones((n, m)) * level ``` 數組中的所有值都初始化為`level`，這通常大于倒塌閾值`K`。 以下是`step `方法，它找到大于`K`的所有細胞并將它們推翻： ```py kernel = np.array([[0, 1, 0], [1,-4, 1], [0, 1, 0]], dtype=np.int32) def step(self, K=3): toppling = self.array > K num_toppled = np.sum(toppling) c = correlate2d(toppling, self.kernel, mode='same') self.array += c return num_toppled ``` 為了解釋這是如何工作的，我將從一小堆開始，只有兩個準備推翻的細胞： ```py pile = SandPile(n=3, m=5, level=0) pile.array[1, 1] = 4 pile.array[1, 3] = 4 ``` 最初，`pile.array`是這樣： ```py [[0 0 0 0 0] [0 4 0 4 0] [0 0 0 0 0]] ``` 現在我們可以選擇高于倒塌閾值的細胞： ```py toppling = pile.array > K ``` 結果是一個布爾數組，但是我們可以像整數數組一樣使用它： ```py [[0 0 0 0 0] [0 1 0 1 0] [0 0 0 0 0]] ``` 如果我們關聯這個數組和核起來，它會在每個`toppling`是 1 的地方復制這個核。 ```py c = correlate2d(toppling, kernel, mode='same') ``` 這就是結果： ```py [[ 0 1 0 1 0] [ 1 -4 2 -4 1] [ 0 1 0 1 0]] ``` 注意，在核的副本重疊的地方，它們會相加。 這個數組包含每個細胞的改變量，我們用它來更新原始數組： ```py pile.array += c ``` 這就是結果： ```py [[0 1 0 1 0] [1 0 2 0 1] [0 1 0 1 0]] ``` 這就是`step`的工作原理。 默認情況下，`correlate2d`認為數組的邊界固定為零，所以任何超出邊界的沙粒都會消失。 `SandPile`還提供了`run`，它會調用`step`，直到沒有更多的細胞倒塌： ```py def run(self): total = 0 for i in itertools.count(1): num_toppled = self.step() total += num_toppled if num_toppled == 0: return i, total ``` 返回值是一個元組，其中包含時間步數和倒塌的細胞總數。 如果你不熟悉`itertools.count`，它是一個無限生成器，它從給定的初始值開始計數，所以`for`循環運行，直到`step`返回 0。 最后，`drop`方法隨機選擇一個細胞并添加一粒沙子： ```py def drop(self): a = self.array n, m = a.shape index = np.random.randint(n), np.random.randint(m) a[index] += 1 ``` 讓我們看一個更大的例子，其中` n=20`： ```py pile = SandPile(n=20, level=10) pile.run() ```  圖 8.1：沙堆模型的初始狀態（左），和經過 200 步（中）和 400 步（右）之后的狀態 初始級別為 10 時，這個沙堆需要 332 個時間步才能達到平衡，共有 53,336 次倒塌。 圖？（左）展示了初始運行后的狀態。 注意它具有重復元素，這是分形特征。 我們會很快回來的。 圖？（中）展示了在將 200 粒沙子隨機放入細胞之后的沙堆構造，每次都運行直至達到平衡。 初始狀態的對稱性已被打破；狀態看起來是隨機的。 最后圖？（右）展示了 400 次放置后的狀態。 它看起來類似于 200 次之后的狀態。 事實上，這個沙堆現在處于穩定狀態，其統計屬性不會隨著時間而改變。 我將在下一節中解釋一些統計屬性。 ## 8.4 重尾分布 如果沙堆模型處于臨界狀態，我們希望為一些數量找到重尾分布，例如雪崩的持續時間和大小。 所以讓我們來看看。 我會生成一個更大的沙堆，`n = 50`，初始水平為 30，然后運行直到平衡狀態： ```py pile2 = SandPile(n=50, level=30) pile2.run() ``` 下面我們會運行 100,000 個隨機放置。 ```py iters = 100000 res = [pile2.drop_and_run() for _ in range(iters)] ``` 顧名思義，`drop_and_run`調用`drop`和`run`，并返回雪崩的持續時間和倒塌的細胞總數。 所以`res`是`(T, S)`元組的列表，其中`T`是持續時間，以時間步長為單位，并且`S`是倒塌的細胞。 我們可以使用`np.transpose`將`res`解構為兩個 NumPy 數組： ```py T, S = np.transpose(res) ``` 大部分放置的持續時間為 1，沒有倒塌的細胞，所以我們會將這些過濾掉。 ```py T = T[T>1] S = S[S>0] ``` `T`和`S`的分布有許多小值和一些非常大的值。 我將使用`thinkstats2`中的`Hist`類創建值的直方圖; 即每個值到其出現次數的映射。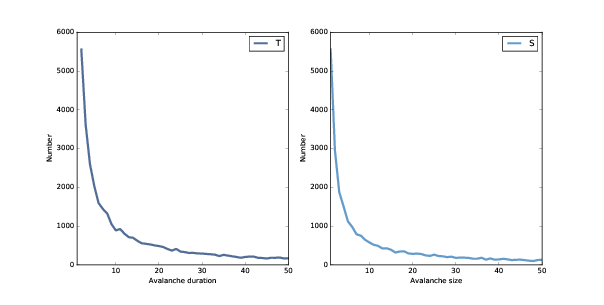 ```py from thinkstats2 import Hist histT = Hist(T) histS = Hist(S) ```  圖 8.2：雪崩持續時間（左）和大小（右）的分布，線性刻度。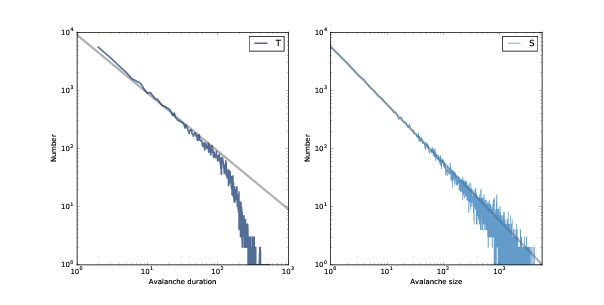  圖 8.3：雪崩持續時間（左）和大小（右）的分布，雙對數刻度。 圖？顯示了值小于 50 的結果。但正如我們在第？節中看到的那樣，我們可以通過將它們繪制在雙對數坐標上，更清楚地了解這些分布，如圖？所示。 對于 1 到 100 之間的值，分布在雙對數刻度上幾乎是直的，這表示了重尾。 圖中的灰線斜率為 -1，這表明這些分布遵循參數為`α=1`的冪律。 對于大于 100 的值，分布比冪律模型下降更快，這意味著較大值比模型的預測更少。 一種解釋是，這種效應是由于沙堆的有限尺寸造成的，因此我們可能預計，更大的沙堆能更好地擬合冪律。 另一種可能性是，這些分布并不嚴格遵守冪律，你可以在本章結尾的一個練習中探索。 但即使它們不是冪律分布，它們仍然是重尾的，因為我們預計系統處于臨界狀態。 ## 8.5 分形 臨界系統的另一個屬性是分形幾何。 圖中的初始狀態 （左）類似于分形，但是你不能總是通過觀察來分辨。 識別分形的更可靠的方法是估計其分形維度，正如第？節那樣。 我首先制作一個更大的沙堆，`n = 131`，初始水平為 22。 ```py pile3 = SandPile(n=131, level=22) pile3.run() ``` 順便說一下，這個沙堆達到平衡需要 28,379 步，超過 2 億個細胞倒塌。 為了更清楚地看到生成的團，我選擇水平為 0, 1, 2 和 3 的細胞，并分別繪制它們： ```py def draw_four(viewer, vals=range(4)): thinkplot.preplot(rows=2, cols=2) a = viewer.viewee.array for i, val in enumerate(vals): thinkplot.subplot(i+1) viewer.draw_array(a==vals[i], vmax=1) ``` `draw_four`需要`SandPileViewer`對象，它在`Sand.py`中定義。 參數`vals`是我們想要繪制的值的列表; 默認值是 0, 1, 2 和 3。 以下是它的使用方式： ```py viewer3 = SandPileViewer(pile3) draw_four(viewer3) ```  圖 8.4：沙堆模型的初始狀態，從上到下，從左到右選擇水平為 0, 1, 2 和 3 的細胞。 圖？展示了結果。 現在對于這些圖案中的每一個，我們都可以使用方框計數算法來估計分形維數：我們將計算沙堆中心的小方框中的細胞數量，然后看看細胞數量隨著方框變大而如何增加。 這是我的實現： ```py def count_cells(a): n, m = a.shape end = min(n, m) res = [] for i in range(1, end, 2): top = (n-i) // 2 left = (m-i) // 2 box = a[top:top+i, left:left+i] total = np.sum(box) res.append((i, i**2, total)) return np.transpose(res) ``` 參數`a`是 NumPy 布爾數組，值為 0 和 1。 方框的大小最初為 1，每次循環中，它會增加 2，直到到達終點，它是`n`和`m`中較小的一個。 每次循環中，`box`都是一組寬度和高度為`i`的細胞，位于數組中心。 `total`是方框中“開”細胞的數量。 結果是一個元組列表，其中每個元組包含`i`和`i ** 2`，用于比較，以及方框中的細胞數量。 最后，我們使用`np.transpose`生成一個 NumPy 數組，其中包含`i`，`i ** 2`和`total`。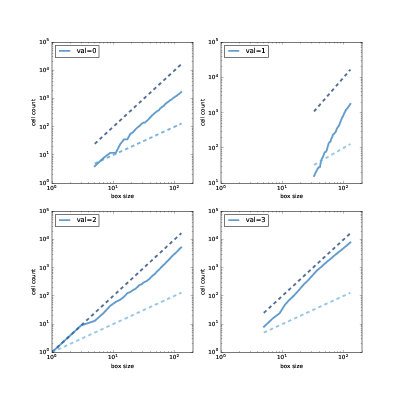 為了估計分形維度，我們提取行： ```py steps, steps2, cells = res ``` 之后繪制結果： ```py thinkplot.plot(steps, steps2, linestyle='dashed') thinkplot.plot(steps, cells) thinkplot.plot(steps, steps, linestyle='dashed') ``` 然后使用`linregress `在雙對數刻度上擬合直線： ```py from scipy.stats import linregress params = linregress(np.log(steps), np.log(cells)) slope = params[0] ```  圖 8.5：與斜率位 1 和 2 的虛線相比，水平為 0, 1, 2 和 3 的細胞的方框計數。 圖？展示了結果。 請注意，只有`val = 2`（左下）從方框大小 1 開始，因為中心細胞的值為 2；其他直線從包含非零細胞數的第一個方框大小開始。 在雙對數刻度上，細胞計數幾乎形成直線，這表明我們正在測量方框大小的有效范圍內的分形維度。 估計的分形維度是： ```py 0 1.871 1 3.502 2 1.781 3 2.084 ``` 值為 0, 1 和 2 的分形維度似乎明顯不是整數，這表明圖像是分形的。 嚴格來說，值為 3 的分形維度與 2 不可區分，但考慮到其他值的結果，線的表觀曲率和圖案的外觀，似乎它也是分形的。 本章結尾的練習之一，要求你使用不同的`n`和`level`值，再次運行此分析，來查看估計的維度是否一致。 ## 8.6 頻譜密度 提出沙堆模型的原始論文的標題是《自組織臨界：1/f 噪聲的解釋》（Self-Organized Criticality: An Explanation of 1/f Noise）。 正如小標題所述的那樣，Bak，Tang 和 Wiesenfeld 正試圖解釋為什么許多自然和工程系統表現出 1/f 噪聲，這也被稱為“閃爍噪聲”和“粉紅噪聲”。 為了了解粉紅噪聲，我們必須繞路來了解信號，頻譜分析和噪聲。 信號： 信號是隨時間變化的任何數量。 一個例子是聲音，即空氣密度的變化。 在本節中，我們將探討雪崩持續時間和大小在不同時間段內的變化。 頻譜分析： 任何信號都可以分解為一組具有不同音量或功率的頻率分量。 例如，演奏中央 C 上方的 A 的小提琴的聲音，包含頻率為 440 Hz 的主要分量，但它也包含較低功率分量，例如 880 Hz，1320 Hz 和其他整數倍的基頻。 頻譜分析是尋找構成信號的成分和它們的功率的過程，稱為其頻譜。 噪聲： 在通常的用法中，“噪聲”通常是一種不需要的聲音，但在信號處理的情況下，它是一個包含許多頻率成分的信號。 噪聲有很多種。 例如，“白噪聲”是一個信號，它在很寬的頻率范圍內擁有相同功率的成分。 其他種類的噪聲在頻率和功率之間有不同的關系。 在“紅噪聲”中，頻率為`f`的功率為`1 / f ** 2`，我們可以這樣寫： ``` P(f) = 1 / f ** 2 ``` 我們可以把指數 2 換成`β`來擴展它： ``` P(f) = 1 / f ** β ``` 當`β= 0`時，該等式描述白噪聲; 當`β= 2`時，它描述紅噪聲。 當參數接近 1 時，我們將結果稱為`1 / f`噪聲。 更一般來說，任何介于 0 和 2 之間的噪聲稱為“粉紅”，因為它介于白色和紅色之間。 那么這如何適用于沙堆模型呢？ 假設每次細胞倒塌時，它會發出聲音。 如果我們在運行中記錄了沙堆模型，它會是什么樣子？ 在我的`SandPile`實現運行時，它會記錄在每個時間步驟中，倒塌的細胞數量，并將結果記錄在名為`toppled_seq`的列表中。 例如，在第？節中運行模型之后，我們可以提取產生的信號： ```py signal = pile2.toppled_seq ``` 為了計算信號的頻譜（同樣，這是它包含的頻率和它們的功率），我們可以使用快速傅立葉變換（FFT）。 唯一的問題是噪聲信號的頻譜往往是嘈雜的。 但是，我們可以通過將一個長信號分成多個段，計算每個段的 FFT，然后計算每個頻率的平均功率來使其平滑。 該算法的一個版本被稱為“韋爾奇方法”，SciPy 提供了一個實現。 我們可以像這樣使用它： ```py from scipy.signal import welch nperseg = 2048 freqs, spectrum = welch(signal, nperseg=nperseg, fs=nperseg) ``` `nperseg`是信號分解成的片段長度。 對于較長的片段，我們可以獲得更多的頻率成分，但由于平均的片段數較少，結果更加嘈雜。 `fs`是“采樣頻率”，即每單位時間的信號中的數據點數。 通過設置`fs = nperseg`，我們可以得到從 0 到`nperseg / 2`的頻率范圍，但模型中的時間單位是任意的，所以頻率并不意味著什么。 返回值，`freqs`和`powers`是 NumPy 數組，包含成分的頻率及其相應的功率。 如果信號是粉紅噪聲，我們預計： ``` P(f) = 1 / f ** β ``` 對兩邊取對數會得到： ``` logP(f) = ?β logf ``` 所以如果我們在雙對數刻度上繪制功率與頻率的關系，我們預計有一條斜率為`β`的直線。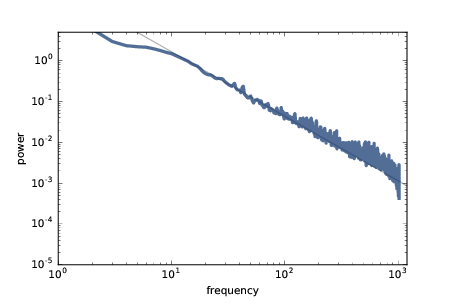  圖 8.6：隨著時間推移的倒塌細胞的功率頻譜，雙對數刻度 圖？顯示結果。 對于 10 到 1000 之間的頻率（以任意單位），頻譜落在一條直線上。 灰線斜率為 -1.58，這對應于由 Bak，Tang 和 Wiesenfeld 報告的參數`β= 1.58`。 這個結果證實了沙堆模型產生粉紅噪聲。 ## 8.7 還原論與整體論 Bak，Tang 和 Wiesenfeld 的原始論文是過去幾十年中被引用次數最多的論文之一。 其他系統已被證明是自組織臨界，特別是沙堆模型已被詳細研究。 事實證明，沙堆模型并不是一個很好的沙堆模型。 沙子密集且不太粘，所以動量對雪崩的行為有著不可忽視的影響。 因此，與模型預測的相比，非常大和非常小的雪崩數量更少，并且分布可能不是重尾。 Bak 建議，這個觀察沒有考慮到這一點。 沙堆模型并是現實的沙堆模型；它旨在成為一大類系統的簡單模型。 為了理解這個要點，考慮兩種模式，還原論和整體論，會有幫助。 還原論模型通過描述系統的各個部分及其相互作用來描述系統。 當還原論模型用于解釋時，它取決于模型和系統組成部分之間的類比。 例如，為了解釋為什么理想氣體定律成立，我們可以用點質量模擬組成氣體的分子，并將它們的相互作用建模為彈性碰撞。 如果你模擬或分析這個模型，你會發現它服從理想的氣體定律。 一定程度上，該模型滿足了，氣體中的分子表現為模型中分子。 類比位于系統的各個部分和模型的各個部分之間。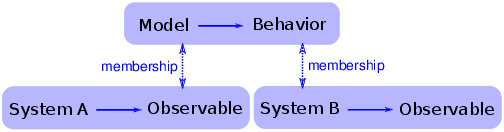  圖 8.7：還原論模型的邏輯結構 整體論模型更關注系統之間的相似性，而對類比部分不太感興趣。 整體論建模方法通常由兩個步驟組成，不一定按以下順序： + 識別出現在各種系統中的一種行為。 + 尋找證明這種行為的簡單模型。 例如，在《自私的基因》（The Selfish Gene）中，理查德道金斯（Richard Dawkins）認為，遺傳進化只是進化系統的一個例子。 他確定了這些類別的基本元素 - 離散復制器（discrete replicator），可變性和差異生殖（differential reproduction） - 并提出任何包含這些元素的系統都會顯示類似的行為，包括不帶設計的復雜性。 作為演化系統的另一個例子，他提出了“模因”（memes），即通過人與人之間的傳播而復制的思想或行為 [2]。 由于模因爭奪人類的注意力的資源，它們的演變方式與遺傳進化相似。 > [2] “模因”的用法源自 Dawkins，并且早于 20 年前這個詞在互聯網上的衍生用法。 模因模型的批評者指出，模因是基因的一個很差的類比。 模因在許多方面與基因不同。 但道金斯認為，這些差異并不重要，因為模因不可能與基因類似。 相反，模因和基因是同一類別的例子：進化系統。 它們之間的差異強調了真正的觀點，即進化是一個適用于許多看似不同的系統的通用模型。 圖？顯示了這個論述的邏輯結構。 Bak 也提出了類似的觀點，即自組織臨界性是一大類系統的通用模型： > 由于這些現象無處不在，它們不能依賴于任何具體的細節......如果一大類問題的物理結果是相同的，這為【理論家】提供了選項，選擇屬于該類的最簡單的可能的【模型】，來進行詳細的研究 [3]。 > [3] Bak, How Nature Works, Springer-Verlag 1996, page 43. 許多自然系統表現出臨界系統的行為特征。 Bak 對這種普遍性的解釋是，這些系統是自組織臨界性的示例。 有兩種方式可以支持這個論點。 一個是建立一個特定系統的現實模型，并顯示該模型表現出 SOC。 其次是證明 SOC 是許多不同模型的一個特征，并確定這些模型共同的基本特征。 第一種方法我稱之為還原論，可以解釋特定系統的行為。 第二種是整體論的方法，解釋了自然系統中臨界性的普遍性。 他們是不同目的的不同模型。 對于還原論模型，現實主義是主要優點，簡單性是次要的。 對于整體模型，這是相反的。 ## 8.8 SOC，因果和預測 如果股市指數在一天內下跌一個百分點，則不需要解釋。 但如果它下降 10%，人們想知道為什么。 電視上的專家愿意提供解釋，但真正的答案可能是沒有解釋。 股票市場的日常變化展示了臨界性的證據：數值變化的分布是重尾的，時間序列表現出粉紅噪音。 如果股票市場是一個臨界系統，我們應該預計，偶爾的巨大變化是市場普通行為的一部分。 地震強度的分布也是重尾的，并且存在可能解釋這種行為的，地質斷層動力學的簡單模型。 如果這些模型是正確的，那就意味著大地震是普遍的； 也就是說，與小地震相比，他們不需要更多解釋。 同樣，查爾斯·佩羅（Charles Perrow）認為，像核電廠這樣的大型工程系統的故障，就像沙堆模型中的雪崩一樣。 大多數故障是小的，孤立的和無害的，但偶爾壞運氣的巧合會產生災難。 當發生重大事故時，調查人員會去尋找原因，但如果佩羅的“正常事故理論”是正確的，那么可能沒有特殊原因導致嚴重故障。 這些結論并不令人欣慰。 除其他事情外，它們意味著大地震和某些事故從根本上是不可預測的。不可能觀察臨界系統的狀態，并說大雪崩是否“來臨”。 如果系統處于臨界狀態，則總是可能發生大型雪崩。 它只取決于下一粒沙子。 在沙堆模型中，大雪崩的原因是什么？哲學家有時會將直接（proximate）原因與根本（ultimate）原因區分開來，前者是最直接的原因，無論出于何種原因，后者被視為真正的原因。 在沙堆模型中，雪崩的直接原因是一粒沙子，但引起大雪崩的沙粒與其他沙粒相同，所以它沒有提供特別的解釋。大雪崩的根本原因是整個系統的結構和動態：大雪崩的發生是因為它們是系統的一個屬性。 許多社會現象，包括戰爭，革命，流行病，發明和恐怖襲擊，其特點是重尾分布。如果這些分布的原因是社會系統是臨界的，那么這表明主要的歷史事件可能從根本上是不可預測的，并且無法解釋。 ## 8.9 練習 練習 1 本章的代碼位于本書倉庫中的 Jupyter 筆記本`chap08.ipynb`中。打開這個筆記本，閱讀代碼，然后運行單元格。你可以使用這個筆記本來練習本章的練習。我的解決方案在`chap08soln.ipynb`中。 練習 2 為了檢驗`T`和`S`的分布是否是重尾的，我們將它們的直方圖繪制在雙對數刻度上，這就是 Bak，Tang 和 Wiesenfeld 在他們的論文中所展示。但我們在第？節中看到，這種可視化可能掩蓋分布的形狀。使用相同的數據，繪制一個圖表，顯示`S`和`T`的累積分布（CDF）。對于他們的形狀你可以說什么？他們是否遵循冪律？他們是重尾的嘛？ 你可能會發現將 CDF 繪制在對數和雙對數刻度上會有所幫助。 練習 3 在第？章，我們發現沙堆模型的初始狀態會產生分形圖案。但是在我們隨機放置了大量的沙粒之后，圖案看起來更隨機。 從第？章中的示例開始，運行沙堆模型一段時間，然后計算 4 個水平中的每個的分形維度。沙堆模型是否處于穩定狀態？ 練習 4 另一種沙堆模型，稱為“單一來源”模型，從不同的初始條件開始：中心細胞設為較大值，除了中心細胞，所有細胞設為 0，而不是所有細胞都是同一水平的。編寫一個創建`SandPile`對象的函數，設置單一來源的初始條件，并運行，直到達到平衡。結果出現了分形嗎？ 你可以在 <http://math.cmu.edu/~wes/sandgallery.html> 上了解這個版本的沙堆模型。 練習 5 在 1989 年的一篇論文中，Bak，Chen 和 Creutz 認為生命游戲是一個 SOC 系統 [5]。 > [5] “Self-organized criticality in the Game of Life”，可以在這里獲取：<http://www.nature.com/nature/journal/v342/n6251/abs/342780a0.html>。 為了復制他們的測試，運行 GoL CA 直到穩定，然后隨機選擇一個細胞并翻轉它。運行 CA 直到它再次穩定下來，跟蹤`T`，這個是它需要的時間步數，以及`S`，受影響的細胞數。重復進行大量試驗并繪制`T`和`S`的分布。同時，記錄在每個時間步驟中改變狀態的細胞數量，并查看得到的時間序列是否與粉紅噪聲相似。 練習 6 在《自然界的分形幾何》（The Fractal Geometry of Nature）中，Benoit Mandelbrot 提出了自然系統中重尾分布的普遍性的解釋，他稱之為“異端”。 正如 Bak 所言，許多系統可以獨立產生這種行為。 相反，它們可能只是少數，但系統之間可能會有交互，它們導致行為的傳播。 為了支持這個論點，Mandelbrot 指出： + 觀測數據的分布通常是“一個固定的底層真實分布，和一個高度可變的過濾器的聯合效應”。 + 重尾分布對于過濾器是健壯的；也就是說，“各種過濾器使其漸近行為保持不變”。 你怎么看待這個觀點？ 你會把它描述為還原論還是整體論？ 練習 7 在 <http://en.wikipedia.org/wiki/Great_man_theory> 上閱讀“偉人”的歷史理論。 自組織臨界對這個理論有什么暗示？