# 五、細胞自動機 > 原文：[Chapter 5 Cellular Automatons](http://greenteapress.com/complexity2/html/thinkcomplexity2006.html) > 譯者：[飛龍](https://github.com/wizardforcel) > 協議：[CC BY-NC-SA 4.0](http://creativecommons.org/licenses/by-nc-sa/4.0/) > 自豪地采用[谷歌翻譯](https://translate.google.cn/) 細胞自動機（CA）是一個世界的模型，帶有非常簡單的物理。 “細胞”的意思是世界被分成一個大口袋，稱為細胞。 “自動機”是一臺執行計算的機器 - 它可能是一臺真機。 ，但更多時候，“機器”是數學抽象或計算機的模擬。 本章介紹了史蒂文沃爾夫勒姆（Steven Wolfram）在 20 世紀 80 年代進行的實驗，表明一些細胞自動機展示出令人驚訝的復雜行為，包括執行任意計算的能力。 我討論了這些結果的含義，在本章的最后，我提出了在 Python 中高效實現 CA 的方法。 本章的代碼位于本書倉庫的`chap05.ipynb`中。 使用代碼的更多信息，請參見第？章。 ## 5.1 簡單的 CA 細胞自動機 [1] 由規則來管理，它決定系統如何即時演化。 時間分為離散的步驟，規則規定了，如何根據當前狀態計算下一個時間步驟中的世界狀態。 > automaton（自動機）的復數為 automatons 或 automata。 作為一個微不足道的例子，考慮帶有單個細胞的細胞自動機（CA）。 細胞狀態是用變量`xi`表示的整數，其中下標`i`表示`xi`是時間步驟`i`期間的系統狀態。 作為初始條件，`x0 = 0`。 現在我們需要一個規則。 我會任意選擇`xi = x[i-1] + 1`，它表示在每個時間步驟之后，CA 的狀態會增加 1。到目前為止，我們有一個簡單的 CA ，執行簡單的計算：它用于計數。 但是這個 CA 是不合規則的；可能的狀態數通常是有限的。 為了使其成立，我將選擇最小的感興趣的狀態數 2，和另一個簡單的規則`xi = (x[i-1] + 1) % 2`，其中`%`是余數（或模）運算符。 這個 CA 的行為很簡單：閃爍。 也就是說，在每個時間步之后，細胞的狀態在 0 和 1 之間切換。 大多數 CA 是確定性的，這意味著規則沒有任何隨機元素；給定相同的初始狀態，它們總是產生相同的結果。 也有不確定性的 CA，但我不會在這里涉及它們。 ## 5.2 Wolfram 的實驗 前一節中的 CA 只有一個細胞，所以我們可以將其視為零維，并且它不是很有趣。 在本章的其余部分中，我們將探索一維（1-D）CA，后者會變得非常有趣。 說 CA 有維度就是說細胞被安排在一個連續的空間中，這樣它們中的一些可以看作“鄰居”。 在一維中，有三種自然形式： 有限序列： 數量有限的細胞排成一排。 除第一個和最后一個之外的所有細胞都有兩個鄰居。 環： 數量有限的細胞排列成一個環。 所有細胞都有兩個鄰居。 無限序列： 數量無限的細胞排列成一排。 確定系統如何即時演化的規則，基于“鄰域”的概念，即“鄰域”，即決定給定細胞的下一個狀態的一組細胞。 在二十世紀八十年代初，斯蒂芬沃爾夫勒姆發表了一系列論文，對一維 CA 進行了系統的研究。 他確定了四大類行為，每一類都比上一個更有趣。 Wolfram 的實驗使用了三個細胞的鄰域：細胞本身及其左右鄰居。 在這些實驗中，這些細胞有兩個狀態，分別表示為 0 和 1，所以規則可以通過一個表格進行匯總，它將鄰域狀態（狀態的三元組）映射為中心細胞的下一個狀態。 下表展示了一個示例： | prev | 111 | 110 | 101 | 100 | 011 | 010 | 001 | 000 | | --- | --- | --- | --- | --- | --- | --- | --- | --- | | next | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 第一行顯示鄰居可能擁有的八個狀態。第二行顯示下一個時間步驟中的中心細胞的狀態。 作為該表的簡明編碼，Wolfram 建議將第二行讀作二進制數。 因為二進制 00110010 是十進制的 50，所以 Wolfram 稱這個 CA 為“規則 50”。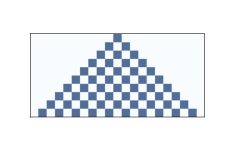  圖 5.1：十個時間步驟之后的規則 50 上圖展示了規則 50 在 10 個時間步驟之后的效果。 第一行展示第一個時間步驟內的系統狀態; 它起始于一個“開”細胞，其余都是“關”。 第二行展示下一個時間步驟中的系統狀態，以此類推。 圖中的三角形是這些 CA 的典型；這是領域形狀的結果嗎？ 在一個時間步驟中，每個細胞都會影響任一方向上的鄰居的狀態。 在下一個時間步驟中，該影響可以在每個方向上向一個細胞傳播。 因此，過去的每個細胞都有一個“影響三角形”，包括所有可能受其影響的細胞。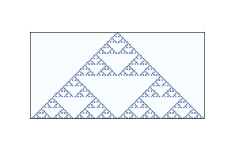 ## 5.3 CA 的分類  圖 5.2：64 個步驟之后的規則 18 有多少種不同的 CA？ 由于每個細胞都處于開或關的狀態，我們可以用一位來指定細胞的狀態。在三個細胞的鄰域中，有 8 種可能的情況，因此規則表中有 8 個條目。由于每個條目都占一個位，我們可以使用 8 位指定一個表。使用 8 位，我們可以指定 256 個不同的規則。 Wolfram 的第一個 CA 實驗就是測試所有 256 種可能性并嘗試對它們進行分類。 在視覺上檢查結果時，他提出 CA 的行為可以分為四類。第一類包含最簡單（也是最不感興趣）的 CA，即從幾乎任何起始條件演變為相同統一圖案的 CA。作為一個簡單的例子，規則 0 總是在一個時間步后產生一個空的圖案。 規則 50 是第二類的一個例子。它生成一個帶有嵌套結構的簡單圖案；也就是說，該圖案包含許多自身的較小版本。規則 18 使嵌套結構更加清晰；圖？顯示了 64 步后的樣子。 這種模式類似于謝爾賓斯基三角形，你可以在 <http://en.wikipedia.org/wiki/Sierpinski_triangle> 上閱讀。 某些二類 CA 生成的圖案復雜而美觀，但與第三和第四類相比，它們相對簡單。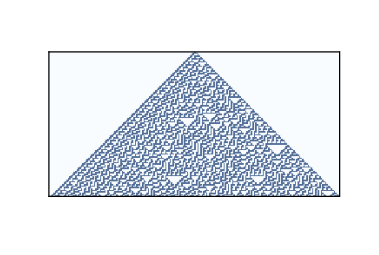 ## 5.4 隨機性  圖 5.3：100 個步驟之后的規則 30 第三類包含產生隨機性的 CA。規則 30 是一個例子；圖？顯示 100 個時間步后的樣子。 左側有一個明顯的圖案，右側有各種大小的三角形，但中心看起來很隨意。 事實上，如果你把中間列看做一個比特序列，就很難將其區分于真正的隨機序列。 它通過了許多統計測試，人們用來測試比特序列是否隨機。 產生看起來隨機的數字的程序，稱為偽隨機數字生成器（PRNG）。 他們不被認為是真正的隨機，因為： + 它們中的許多產生規律性序列，可以通過統計來檢測。 例如，C 標準庫中的`rand`的原始實現，使用了線性同余生成器，生成器生成的序列具有易于檢測的序列相關性。 + 任何使用有限狀態（即存儲）的 PRNG 最終都會重復。 生成器的特點之一就是這種重復周期。 + 底層過程基本上是確定性的，不同于一些物理過程，如放射性衰減和熱噪聲，被認為是基本隨機的。 現代 PRNG 產生的序列，在統計上與隨機值無法區分，并且它們以很長的周期實現，以至于在重復之前宇宙將崩潰。 這些發生器的存在，提出了一個問題，即質量好的偽隨機序列與由“真正的”隨機過程產生的序列之間，是否存在真正差異。 在“A New Kind of Science”中，沃爾夫勒姆認為沒有（第 315-326 頁）。 ## 5.5 確定性 第三類 CA 的存在令人驚訝。 為了解釋多么令人驚訝，讓我從哲學確定性（決定論）開始（參見<http://en.wikipedia.org/wiki/Determinism>）。 許多哲學立場很難準確定義，因為它們有不同的風味。 我經常發現，使用從弱到強排列的陳述列表，來定義它們是有用的： D1： 確定性模型可以對某些物理系統做出準確的預測。 D2： 許多物理系統可以用確定性過程建模，但有些系統本質上是隨機的。 D3： 所有事件都是由先驗事件造成的，但許多物理系統基本上是不可預測的。 D4： 所有事件都是由先驗事件造成的，并且可以（至少原則上）預測。 我構建這個范圍的目標是，讓 D1 如此弱以至于幾乎每個人都會接受它，D4 如此強以至于幾乎沒有人會接受它，并且有些人會接受中間的陳述。 作為對歷史發展和科學發現的回應，世界輿論的質心沿著這個范圍擺動。 在科學革命之前，許多人認為宇宙的運作基本上是不可預測的，或由超自然力量所控制。 在牛頓力學的勝利之后，一些樂觀主義者開始相信像 D4 這樣的東西；例如，皮埃爾-西蒙拉普拉斯（Pierre-Simon Laplace）在 1814 年寫道： > 我們可以把宇宙的現狀看作過去的果和未來的因。 一個智能在某個特定的時刻，知道所有使自然運動的力量，以及構成自然的所有物品的所有位置，如果它也足夠大，來提交這些數據用于分析，它會將宇宙最大的天體和最小的原子的運動匯總成一個公式； 對于這樣的智能來說，沒有什么是不確定的，未來就像過去一樣會存在于它的眼前。 這種“智能”被稱為“拉普拉斯的惡魔”。見 <http://en.wikipedia.org/wiki/Laplace's_demon>。 在這種情況下，“惡魔”這個詞具有“精神”的意義，沒有邪惡的含義。 19 世紀和 20 世紀的發現逐漸打破了拉普拉斯的希望。 熱力學，放射性和量子力學對強式的決定論構成了連續的挑戰。 在 20 世紀 60 年代，混沌理論表明，在某些確定性系統中，預測只能在短時間尺度上進行，并受初始條件測量精度的限制。 大多數這些系統，是空間連續（不是時間）和非線性的，所以它們行為的復雜性并不令人驚訝。 沃爾夫勒姆在簡單的細胞自動機中展示的復雜行為更令人驚訝，并且令人不安，至少對于確定性的世界觀來說。 到目前為止，我一直關注對確定性的科學挑戰，但是最持久的反對意見是確定性與人類自由意志之間的沖突。 復雜性科學為這種明顯的沖突提供了可能的解決方案; 我將在第？章中回到這個話題。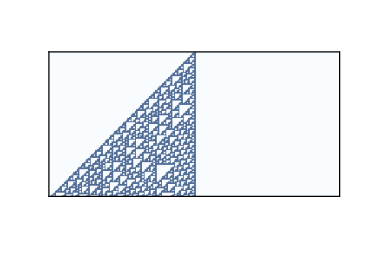 ## 5.6 飛船  圖 5.4：100 步之后的規則 110 第四類 CA 的行為更令人驚訝。 幾個一維 CA，最著名的是規則 110，是圖靈完備的，這意味著他們可以計算任何可計算的函數。 這個屬性也稱為普遍性，由 Matthew Cook 在 1998 年證明。請參閱 <http://en.wikipedia.org/wiki/Rule_110>。 圖？展示了初始條件為單個細胞和 100 個時間步驟的規則 110 的樣子。 在這個時間尺度上，沒有發生什么特別的事情。 有一些有規律的模式，但也有一些難以表述的特征。 圖？展示了更大的圖像，它起始于一個隨機的初始條件和 600 個時間步驟：  圖 5.5：初始條件隨機和 600 個時間步驟的規則 110 經過大約 100 個步驟后，背景變成了簡單的重復模式，但背景中有一些持久性結構表現為干擾。 其中一些結構是穩定的，所以它們表現為垂直線條。 其他的在空間中平移，表現為不同斜率的對角線，取決于它們移動一列所需的時間步數。 這些結構被稱為飛船。 飛船之間的碰撞產生不同的結果，取決于飛船的類型和它們碰撞時的階段。 一些碰撞殲滅兩艘船，其他船只保持不變；還有一些產生不同類型的一艘或多艘船只。 這些碰撞是 CA 規則 110 中的計算基礎。 如果你將飛船視為通過電線傳播的信號，并將碰撞視為計算 AND 和 OR 等邏輯運算的門，那么你可以看到 CA 執行計算的意義。 ## 5.7 通用性 為了理解通用性，我們必須理解可計算性理論，它關于計算模型和計算的東西。 最通用的計算模型之一是圖靈機，它是由艾倫圖靈在 1936 年提出的一種抽象計算機。圖靈機是一個一維 CA，兩個方向上都是無限的，并增加了一個讀寫頭。在任何時候，頭部都位于一個細胞上。它可以讀取該細胞的狀態（通常只有兩種狀態），并可以將新值寫入細胞中。 此外，該機器還有一個寄存器，用于記錄機器的狀態（有限數量的狀態之一）和一張規則表。對于每個機器狀態和細胞狀態，表格規定一個操作。操作包括修改頭部所在的細胞，并向左或向右移動一個細胞。 圖靈機并不是計算機的實際設計，但它模擬了常見的計算機體系結構。對于在真實計算機上運行的給定程序，（至少原則上）可以構造一個執行等效計算的圖靈機。 圖靈機很有用，因為它可以刻畫一組圖靈機可以計算的函數，這就是圖靈所做的事情。 這個集合中的函數被稱為圖靈可計算的。 說圖靈機可以計算任何圖靈可計算函數，是一個贅述：根據定義它是真的。 但圖靈可計算性比這更有趣。 事實證明，任何人提出的每個合理的計算模型都是圖靈完備的；也就是說，它可以計算與圖靈機完全相同的一組函數。 其中一些模型，如 lamdba 演算，與圖靈機非常不同，所以它們的等價性令人驚訝。 這種觀察產生了丘奇-圖靈理論，它基本上定義了可計算的含義。 這個“理論”是，圖靈可計算性是可計算性的正確，或至少是自然定義，因為它描述了這種計算模型的多樣化集合的威力。 CA 規則 110是另一種計算模型，其簡單性非常出色。 它也是通用的，為丘奇-圖靈理論提供了支持。 在“A New Kind of Science”中，沃爾夫勒姆闡述了這個理論的一個變種，他稱之為“計算等價性原理”： 幾乎所有不明顯的簡單過程，都可以看作是具有復雜性相同的計算。 更具體來說，計算等價性原理表明，在自然界中發現的系統可以執行達到最高（“通用”）級別的計算能力的計算，并且大多數系統實際上實現了這種最高級別的計算能力。 因此，大多數系統在計算上是等效的（參見 <http://mathworld.wolfram.com/PrincipleofComputationalEquivalence.html>）。 將這些定義應用于 CA，第一類和第二類“顯然很簡單”。 第三類可能不那么明顯，但在某種程度上，完美的隨機性就像完美的順序一樣簡單；復雜性存在于中間。 所以 Wolfram 聲稱第四類行為在自然界中很常見，并且幾乎所有表現它的系統在計算上都是等價的。 ## 5.8 可證偽性 沃爾夫勒姆認為，他的原則比丘奇圖靈理論更強大，因為它是關于自然界的，而不是抽象的計算模型。但是說自然過程“可以看作計算”，使我覺得像理論選擇的陳述。而不僅僅是自然世界的假設。 此外，對于像“幾乎”和“明顯簡單”這樣的未定義術語的資格，他的假設可能是不可證偽的。可證偽性是科學哲學的一個觀點，由卡爾波普爾（Karl Popper）提出，作為科學假說與偽科學之間的界限。如果一個假設是假的，并且有一個實驗，至少在實用性領域，它能反駁這個假設，那么這個假設是可證偽的。 例如，地球上的所有生命都來自共同祖先的說法是可證偽的，因為它對現代物種（在其他東西中）的基因相似性做出了特定的預測。如果我們發現了一種新物種，它的 DNA 與我們的 DNA 幾乎完全不同，那么這就反駁了共同血統理論（或者至少引起質疑）。 另一方面，所謂“神創論”，即所有物種都是由超自然力量創造出來的，是不可證實的，因為沒有任何我們可以觀察到的，與自然世界相矛盾的東西。任何實驗的結果都可以歸因于創作者的意志。 不可證偽的假設可能有吸引力，因為不可能反駁它們。如果你的目標是永遠不會被證明是錯誤的，你應該盡可能選擇不可證偽的假設。 但是，如果你的目標是對世界做出可靠的預測 - 而這至少是科學的目標之一 - 那么不可證偽的假設是無用的。問題是他們沒有結果（如果他們有結果，他們將是可證偽的）。 例如，如果神創論是真實的，那我知道它有什么好處呢？它不會告訴我任何造物主的事情，除了他有一種“對甲蟲的非常喜愛”（歸因于 J. B. S. Haldane）。不同于共同血統理論，它通告許多科學和生物工程領域，理解這個世界或者為之行動是沒有用的。 ## 5.9 這是什么模型？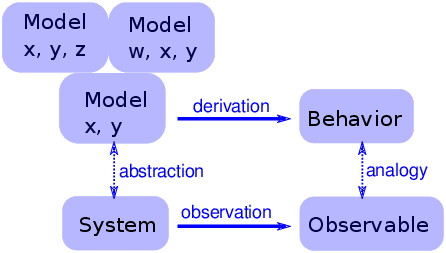  圖 5.6：一個簡單物理模型的邏輯結構 一些細胞自動機主要是數學工藝品。 它們很有趣，因為它們令人驚訝，或者有用，或者漂亮，或者因為它們提供了創建新式數學的工具（比如丘奇圖靈定理）。 但是，它們是不是物理系統的模型還并不清楚。 如果他們是，他們是高度抽象的，也就是說他們并不很詳細或現實。 例如，某些錐螺物種在它們的殼上產生圖案，類似于由細胞自動機產生的圖案（參見`en.wikipedia.org/wiki/Cone_snail`）。 所以假設 CA 是隨著殼長大而在殼上產生圖案的機制的模型，這是很自然的。 但是，至少在最初階段，模型元素（所謂的細胞，鄰居之間的通信，規則）如何對應成長的蝸牛（真實細胞，化學信號，蛋白質交互網絡）的元素，還并不清楚。 對于傳統的物理模型，現實是一種優點。如果模型的元素對應物理系統的元素，則模型和系統之間有明顯的類比。總的來說，我們期望更現實的模型能夠做出更好的預測，并提供更可信的解釋。 當然，這只是一個事實。更詳細的模型更難以處理，并且通常不太適合分析。在某些時候，模型變得如此復雜，以至于直接對系統進行實驗更容易。 在另一個極端，簡單的模型可以完全引人注目，因為它們很簡單。 簡單模型提供了與詳細模型不同的解釋。使用詳細的模型，論述就像這樣：“我們對物理系統`S`感興趣，所以我們構造了一個詳細模型`M`，并且通過分析和模擬表明`M`表現出一種行為`B`，它與實際系統的觀察`O`（定性或定量地）相似。那么為什么`O`會發生？因為`S`類似于`M`，而`B`類似于`O`，我們可以證明`M`導致`B`。” 使用簡單的模型，我們不能說`S`與`M`相似，因為它不是。 相反，論述是這樣的：“有一組模型共享一組共同的特征。 任何具有這些特征的模型都表現出行為`B`。如果我們進行類似于`B`的觀察`O`，解釋它的一種方式是，這表明系統`S`具有足以產生`1`的一組特征。” 對于這種說法，增加更多的特征并沒有幫助。 使模型更真實不會使模型更可靠；它只掩蓋了導致`O`的基本特征，和`S`特有的附帶特征之間的差異。 圖？顯示了這種模型的邏輯結構。 特征`x`和`y`足以產生行為。 增加更多細節，如特征`w`和`z`，可能會使模型更加逼真，但是這種現實并沒有增加解釋力。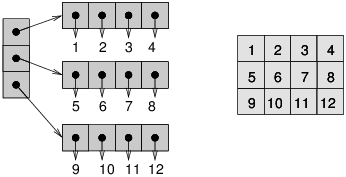 ## 5.10 CA 的實現  圖 5.7：列表的列表（左）和 NumPy 數組（右） 為了生成本章中的圖形，我編寫了一個名為 CA 的 Python 類，它代表細胞自動機，以及用于繪制結果的類。在接下來的幾節中，我會解釋他們如何工作。 為了存儲 CA 的狀態，我使用了 NumPy 數組，這是一個多維數據結構，其元素類型都相同。它與嵌套列表類似，但通常更小更快。圖？說明了原因。左側的圖展示了整數列表的列表；每個點表示一個引用，它占用 4-8 個字節。要訪問其中的一個整數，你必須跟隨兩個引用。 右圖顯示了相同整數的數組。因為這些元素大小都相同，所以它們可以連續存儲在內存中。這種安排節省了空間，因為它不使用引用，并且節省了時間，因為可以直接從下標計算元素的位置；沒有必要跟隨一系列的引用。 為了解釋我的代碼如何工作，我將以一個 CA 開始，它計算每個鄰域中細胞的“奇偶性”。如果數字是偶數，則數字的奇偶性為 0；如果數字為奇數，則奇偶性為 1。 首先，我在第一行的中間，創建帶有單個 1 的零數組。 ```py >>> rows = 5 >>> cols = 11 >>> ca = np.zeros((rows, cols)) >>> ca[0, 5] = 1 print(ca) [[ 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]] ``` `plot_ca`用圖形展示了結果。 ```py mport matplotlib.pyplot as plt def plot_ca(ca, rows, cols): cmap = plt.get_cmap('Blues') plt.imshow(array, interpolation='none', cmap=cmap) ``` 按照約定，我使用縮寫名稱`plt`引入了`pyplot`。 `imshow`將數組視為“圖像”并顯示它。 使用顏色表`'Blues'`，將“開”細胞繪制為深藍色，“關”細胞繪制為淡藍色。 現在，為了計算下一個時間步中的 CA 狀態，我們可以使用`step`： ```py def step(array, i): rows, cols = array.shape for j in range(1, cols): array[i, j] = sum(array[i-1, j-1:j+2]) % 2 ``` 參數`ca`是表示 CA 狀態的 NumPy 數組。 `rows`和`col`是數組的維數，而`i`是我們應該計算的時間步驟的索引。 我用`i`來表示數組的行，它們對應于時間，`j`表示對應于空間的列。 在`step`內部，我們遍歷第`i`行的元素。 每個元素是來自上一行的三個元素的總和，并對 2 取余。 ## 5.11 互相關 上一節中的`step`函數很簡單，但速度并不是很快。 一般來說，如果我們用 NumPy 操作替換循環，我們可以加速這樣的操作，因為 Python 解釋器中的`for`循環會產生大量開銷。 在本節中，我將展示如何使用NumPy函數相關來加快步驟。 首先，我們可以使用數組乘法來代替切片運算符來選擇鄰域。 具體來說，我們將數組乘以一個窗口，其中我們想要選擇的細胞為一，其余為零。 例如，以下窗口選擇前三個元素： ```py >>> window = np.zeros(cols, dtype=np.int8) >>> window[:3] = 1 >>> print(window) [1 1 1 0 0 0 0 0 0 0 0] ``` 如果我們乘以數組的最后一行，我們會得到前三個元素： ```py >>> print(array[4]) >>> print(window * array[4]) [0 1 0 0 0 1 0 0 0 1 0] [0 1 0 0 0 0 0 0 0 0 0] ``` 現在我們可以使用`sum`和模運算符來計算下一行的第一個元素： ```py >>> sum(window * array[4]) % 2 1 ``` 如果我們將窗口向右移動，它會選擇接下來的三個元素，以此類推。所以我們可以像這樣重寫`step`： ```py def step2(array, i): rows, cols = array.shape window = np.zeros(cols) window[:3] = 1 for j in range(1, cols): array[i, j] = sum(window * array[i-1]) % 2 window = np.roll(window, 1) ``` `roll`將窗口向右移動（它也把末尾的補在開頭，但不影響這個函數）。 `step2`產生`step`的相同結果。 它仍然不是非常快，但是它朝著正確的方向邁出了一步，因為我們剛剛執行的操作（乘以窗口，將結果相加，移動窗口并重復）用于各種應用。 它被稱為互相關，而 NumPy 提供了一個稱為`correlate`的函數來計算它。 我們可以用它來編寫更快，更簡單的步驟： ```py def step3(array, i): window = np.array([1, 1, 1]) array[i] = np.correlate(array[i-1], window, mode='same') % 2 ``` 當我們使用`np.correlate`時，窗口不必與數組大小相同，因此使窗口更簡單一些。 `mode `參數決定結果的大小。 你可以閱讀 NumPy 文檔中的詳細信息，但是當模式為`'same'`時，結果與輸入大小相同。 ## 5.12 CA 表 現在還差一步。 如果 CA 規則僅取決于鄰居的總和，那么我們迄今為止的函數仍然有效，但大多數規則還取決于哪些鄰居是開或者關的。 例如，100 和 001 可能會產生不同的結果。 我們可以使用一個包含元素`[4,2,1]`的窗口，使`step`更加通用，它將鄰域解釋為一個二進制數。 例如，鄰域 100 產生 4；010 產生 2，001 產生 1。然后我們可以在規則表中查找這些結果。 以下是更一般的步驟： ```py def step4(array, i): window = np.array([4, 2, 1]) corr = np.correlate(array[i-1], window, mode='same') array[i] = table[corr] ``` 前兩行幾乎相同。 最后一行在`table`中查找`corr`的每個元素，并將結果賦給`array[i]`。 最后，這是計算表的函數： ```py def make_table(rule): rule = np.array([rule], dtype=np.uint8) table = np.unpackbits(rule)[::-1] return table ``` 參數`rule`是一個 0 到 255 的整數。第一行將規則放入單個元素的數組中，以便我們可以使用`unpackbits`，將規則編號轉換為其二進制表示形式。 例如，以下是規則 150 的表： ```py >>> table = make_table(150) >>> print(table) [0 1 1 0 1 0 0 1] ``` 在`thinkcomplexity.py`中，你將找到CA的定義，它封裝了本節中的代碼，以及兩個繪制 CA 的類，`PyplotDrawer`和`EPSDrawer`。 ## 5.13 練習 練習 1 本章的代碼位于本書倉庫的 Jupyter 筆記本`chap05.ipynb`中。打開這個筆記本，閱讀代碼，然后運行單元格。你可以使用這個筆記本來做本章的練習。我的解決方案在`chap05soln.ipynb`中。 練習 2 這個練習要求你試驗規則 110 以及它的一些飛船。 1. 閱讀規則 110 的維基百科頁面，其中描述了其背景圖案和飛船：<https://en.wikipedia.org/wiki/Rule_110>。 1. 使用產生穩定背景圖案的初始條件創建 CA 規則 110。 請注意，CA 類提供了`start_string`，它允許你使用 1 和 0 的字符串初始化數組的狀態。 1. 通過在行的中心添加不同的圖案來修改初始條件，并查看哪些產生了飛船。對于一些`n`的合理的值，你可能想列舉所有可能的`n`位圖案。對于每個飛船，你能找到平移的時間和速度嗎？你能找到的最大的飛船是什么？ 1. 當宇宙飛船相撞時會發生什么？ 練習 3 這個練習的目標是實現一個圖靈機。 1. 閱讀 <http://en.wikipedia.org/wiki/Turing_machine> 來了解圖靈機。 1. 編寫一個名為`Turing`的類來實現圖靈機。對于動作表，使用三個狀態的 Busy Beaver 的規則。 1. 寫一個名為`TuringDrawer`的類，該類生成一個圖像，表示磁帶狀態以及磁頭位置和狀態。可能的外觀的一個示例，請參閱 <http://mathworld.wolfram.com/TuringMachine.html>。 練習 4 1. 本練習要求你執行并測試幾個 PRNG。為了進行測試，你需要安裝 DieHarder，你可以從 <https://www.phy.duke.edu/~rgb/General/dieharder.php> 下載 DieHarder，也可能為你的操作系統作為軟件包提供。 1. 編寫一個程序，實現 <http://en.wikipedia.org/wiki/Linear_congruential_generator> 中描述的線性同余生成器之一。使用 DieHarder 進行測試。 1. 閱讀 Python`random`模塊的文檔。它使用了什么 PRNG？測試它。 1. 使用幾百個細胞實現 CA 規則 30，在合理的時間內以盡可能多的時間步驟運行它，然后將中心列輸出為位序列。測試它。 練習 5 可證偽性是一個吸引人的和有用的想法，但在科學哲學家中，它并不普遍視為界限的解決方案，正如波普爾所聲稱的那樣。 閱讀 <http://en.wikipedia.org/wiki/Fififiability> 并回答以下問題。 1. 界限問題是什么？ 1. 根據波普爾的說法，可證偽性是否解決了界限問題？ 1. 給出兩個理論示例，一個被認為是科學，另一個被認為是非科學，它們由可證偽性的標準成功地區分開。 1. 你能總結出科學哲學家和歷史學家對波普爾的主張提出的，一個或多個反對意見嗎？ 1. 你是否有這樣的感覺，即實踐哲學家對波普爾的工作給予高度評價？