## 十二、合作進化 > 原文：[Chapter 12 Evolution of cooperation](http://greenteapress.com/complexity2/html/thinkcomplexity2012.html) > 譯者：[飛龍](https://github.com/wizardforcel) > 協議：[CC BY-NC-SA 4.0](http://creativecommons.org/licenses/by-nc-sa/4.0/) > 自豪地采用[谷歌翻譯](https://translate.google.cn/) 在最后一章中，我們提出兩個問題，一個來自生物學，一個來自哲學： + 在生物學中，“利他主義問題”是自然選擇與利他主義之間的明顯沖突，自然選擇表明動物生存在不斷競爭的狀態中來生存和繁殖，利他主義是許多動物幫助其他動物的傾向，甚至是顯然對他們不利。見 <https://en.wikipedia.org/wiki/Altruism_(biology)>。 + 在道德哲學中，人性問題是，人類是否從根本上是善良的，或者邪惡的，或者是由環境塑造的空白狀態。見 <https://en.wikipedia.org/wiki/Human_nature>。 我們將用來解決這些問題的工具，（同樣）是基于智能體的模擬和博弈論，博弈論是一組抽象模型，旨在描述智能體交互的各種方式。具體來說，我們會考慮囚徒困境。 本章的代碼位于`chap12.ipynb`中，該書是本書倉庫中的`Jupyter`筆記本。使用此代碼的更多信息，請參見第？節。 ## 12.1 囚徒困境 囚徒困境是博弈論中的一個話題，但它不是一種有趣的博弈。相反，這種博弈揭示了人類的動機和行為。以下是來自維基百科的它的介紹（<http://en.wikipedia.org/wiki/Prisoner's_dilemma>）： 兩名犯罪團伙成員被逮捕并囚禁。每個囚犯都被單獨監禁，無法與另一方交流。檢察官缺乏足夠的證據，來證明這兩個人的主要指控。他們希望以較輕的指控被判處兩年徒刑。同時，檢察官為每個囚犯提供商量的余地。每個囚犯都有機會：（1）通過證明對方犯罪出賣對方，或（2）通過保持沉默與另一方合作。出價是： + 如果 A 和 B 各自背叛對方，每個人都服刑 2 年。 + 如果 A 背叛 B 但 B 保持沉默，A 將被釋放，B 將被監禁 3 年（反之亦然）。 + 如果 A 和 B 都保持沉默，他們兩人只會服刑 1 年（較輕的質控）。 很顯然，這種情況是假想的，但它用于代表各種不同的互動，其中智能體必須選擇是相互“合作”還是“背叛”，以及每個智能體的獎勵（或懲罰）取決于他人的選擇。 有了這套獎懲，我們很有可能說智能體應該合作，也就是說，雙方都應該保持沉默。 但兩個智能體不知道對方會做什么，所以每個人都必須考慮兩種可能的結果。 首先，從 A 的角度來看它： + 如果 B 保持沉默，A 最好是背叛；他會無罪而不是服刑 1 年。 + 如果 B 背叛，A 最好也是背叛；他只會服刑 2 年而不是 3 年。 不管 B 做什么，A 最好都是背叛。 而且因為博弈是對稱的，所以從 B 的角度來看這個分析是一樣的：不管 A 做什么，B 最好也是背叛。 在這個博弈的最簡單版本中，我們假設 A 和 B 沒有考慮其他因素。 他們不能互相溝通，所以他們不能協商，作出承諾或相互威脅。 他們只考慮直接目標，最小化他們的判決；他們不考慮任何其他因素。 在這些假設下，兩個智能體的理性選擇都是背叛。 這可能是一件好事，至少在刑事司法方面是這樣。 但對囚犯來說，這令人沮喪，因為顯然，他們無法獲得他們雙方都想要的結果。 而且這種模式適用于現實生活中的其他場合，其中合作有更大的好處以及對于玩家來說都會更好。 研究這些場景以及擺脫困境的方法，博弈論研究者關注的焦點，但這不是本章的重點。 我們正朝著不同的方向前進。 ## 12.2 善良的問題 自 20 世紀 50 年代，囚徒困境被首次討論以來，它一直是社會心理學研究的熱門話題。根據前一節的分析，我們可以說一個理想的智能體應該做什么; 很難預測真正的人究竟做了些什么。 幸運的是，實驗已經完成了 [1]。 > [1] 這里有一個最近的報告，提到以前的實驗：Barreda-Tarrazona, Jaramillo-Gutiérrez, Pavan, and Sabater-Grande, “Individual Characteristics vs. Experience: An Experimental Study on Cooperation in Prisoner’s Dilemma", Frontiers in Psychology, 2017; 8: 596. <https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5397528/>。 如果我們假設人們足夠聰明地進行分析（或者在解釋時理解它），并且他們通常為了自己的利益而行事，那么我們預計他們幾乎總是背叛。 但他們沒有。 在大多數實驗中，受試者的合作遠遠超過理性的智能體模型的預測 [2]。 > [2] 有個不錯的視頻歸納了我們目前討論的內容：<https://www.youtube.com/watch?v=t9Lo2fgxWHw>。 這個結果最明顯的解釋是，人們不是理性的智能體，這對任何人都不應該感到驚訝。 但為什么不是呢？ 是因為他們不夠聰明，無法理解這種情況，還是因為他們故意違背自己的利益行事？ 根據實驗結果，似乎至少有一部分解釋是純粹的利他主義：許多人愿意為了讓別人受益而承擔成本。現在，在你提出《Journal of Obvious Results》上發表的結論之前，讓我們繼續問為什么： + 為什么人們會幫助別人，即使自己會付出代價？至少部分原因是他們想這樣；這讓他們對自己和世界感覺良好。 + 為什么善良讓人感覺良好？誘人的說法是，有人跟他們提出這是正確的，或者更普遍來說，他們被社會訓練為想要做好事。但毫無疑問 [3]，至少有一大部分利他主義是天生的；在不同程度上，利他主義的傾向是正常大腦發育的結果。 + 那么，為什么呢？大腦發育的內在部分，以及隨后的個體特征，是基因的結果。當然，基因與利他主義的關系是復雜的，可能有許多基因與環境因素相互作用，導致人們在不同情況下或多或少是無私的。盡管如此，幾乎可以肯定的是基因導致人們變得無私。 + 最后，為什么呢？如果在自然選擇下，動物為了生存和繁殖而彼此不斷競爭，似乎顯然利他主義會適得其反。在一個種群中，有些人幫助別人，甚至是為別人傷害自己，其他人純粹是自私的，似乎自私者會受益，利他者會受到影響，并且利他主義的基因將被驅逐而滅絕。 > [3] 我希望你能原諒我在這里用“毫無疑問”代替實驗的參考資料，我想在本章中介紹一些理由，而不會陷入太深。 這個明顯的矛盾是“利他主義問題”：為什么利他主義的基因沒有消失？ 在生物學家中，有很多可能的解釋，包括互惠利他主義，性選擇，親屬選擇和群體選擇。而在非科學家中，還有更多的解釋。我把它交給你去探索別的假說；現在我想專注于一種解釋，可以說是最簡單的一種解釋：也許利他主義是適應性的。換句話說，利他主義的基因可能使人們更容易生存和繁殖。 事實證明，引發利他主義問題的囚徒困境，也可能有助于解決問題。 ## 12.3 囚徒困境比賽 在 20 世紀 70 年代后期，密歇根大學的政治學家羅伯特阿克塞爾羅德（Robert Axelrod）組織了一場比賽來比較囚徒困境（PD）的策略。 他邀請參與者以計算機程序的形式提交策略，然后相互對抗并保持得分。具體來說，他們玩的是 PD 的迭代版本，其中智能體針對同一對手進行多輪比賽，因此他們的決定可以基于歷史。 在 Axelrod 的比賽中，一個簡單的策略出人意料地好，稱為“針鋒相對”，即 TFT，TFT 在第一輪迭代比賽中總是合作；之后，它會復制上一輪對手所做的任何事情。對手繼續合作，TFT 保持合作，如果對手任何時候都背叛，下一輪 TFT 背叛，但如果對手變回合作，TFT 也會合作。 這些比賽的更多信息，以及 TFT 為何如此出色的解釋，請參閱以下視頻：<https://www.youtube.com/watch?v=BOvAbjfJ0x0>。 看看這些比賽中表現出色的策略，Alexrod 發現了他們傾向于分享的特點： + 善良：表現好的策略在第一輪比賽中合作，并且通常會在隨后的幾輪中合作。 + 報復：始終合作的策略，并不如如果對手背叛就報復的策略好。 + 寬恕：但是過于斗氣的策略往往會懲罰自己以及對手。 + 不嫉妒：一些最成功的策略很少超過對手；他們成功了，因為他們對各種各樣的對手都做得足夠好。 TFT 具有所有這些屬性。 Axelrod 的比賽為利他主義問題提供了部分可能的答案：也許利他主義的基因是普遍存在的，因為它們是適應性的。 許多社會互動可以建模為囚徒困境的變種，就這種程度而言，如果將一個大腦設定為善良，平衡報復和寬恕，就會在各種各樣的情況下表現良好。 但是 Axelrod 比賽中的策略是由人們設計的；他們并不進化。 我們需要考慮，善良、報復和寬恕的基因是否可以通過突變出現，成功侵入其他策略的種群，并抵制后續突變的侵入。 ## 12.4 合作進化的模擬 合作進化是第一本書的標題，Axelrod 展示了來自囚徒困境比賽的結果，并討論了利他主義問題的影響。 從那以后，他和其他研究人員已經探索了 PD 比賽的進化動態性，也就是說，PD 選手的總體中，策略的分布隨時間如何變化。 在本章的其余部分中，我運行這些實驗的一個版本并展示結果。 首先，我們需要一種將 PD 策略編碼為基因型的方法。 在這個實驗中，我考慮了一些策略，其中智能體每一輪的選擇僅取決于前兩輪中對手的選擇。 我用字典來表示策略，它將對手的前兩個選擇映射為智能體的下一個選擇。 以下是這些智能體的類定義： ```py class Agent: keys = [(None, None), (None, 'C'), (None, 'D'), ('C', 'C'), ('C', 'D'), ('D', 'C'), ('D', 'D')] def __init__(self, values, fitness=np.nan): self.values = values self.responses = dict(zip(self.keys, values)) self.fitness = fitness ``` `keys`是每個智能體的詞典中的鍵序列，其中元組`('C', 'C')`表示對手在前兩輪合作；`(None, 'C')`意味著只有一輪比賽并且對手合作；`(None, None)`表示還沒有回合。 在`__init__`方法中，`values `是對應于鍵的一系列選項，`'C'`或`'D'`。 所以如果值的第一個元素是`'C'`，那就意味著這個智能體將在第一輪合作。 如果值的最后一個元素是`'D'`，那么如果對手在前兩輪中背叛，該智能體將會背叛。 在這個實現中，總是背叛的智能體的基因型是`'DDDDDDD'`; 總是合作的智能體的基因型是`'CCCCCCC'`，而 TFT 的基因型是`'CCDCDCD'`。 `Agent`類提供`copy`，它使其它智能體具有相同的基因型，但具有一定的變異概率： ```py prob_mutate = 0.05 def copy(self): if np.random.random() > self.prob_mutate: values = self.values else: values = self.mutate() return Agent(values, self.fitness) ``` 突變的原理是，在基因型中選擇一個隨機值并從`'C'`翻轉到`'D'`，或者相反： ```py def mutate(self): values = list(self.values) index = np.random.choice(len(values)) values[index] = 'C' if values[index] == 'D' else 'D' return values ``` 既然我們有了智能體，我們還需要比賽。 ## 12.5 `Tournament` `Tournament`類封裝了 PD 比賽的細節： ```py payoffs = {('C', 'C'): (3, 3), ('C', 'D'): (0, 5), ('D', 'C'): (5, 0), ('D', 'D'): (1, 1)} num_rounds = 6 def play(self, agent1, agent2): agent1.reset() agent2.reset() for i in range(self.num_rounds): resp1 = agent1.respond(agent2) resp2 = agent2.respond(agent1) pay1, pay2 = self.payoffs[resp1, resp2] agent1.append(resp1, pay1) agent2.append(resp2, pay2) return agent1.score, agent2.score ``` `payoffs`是一個字典，將從智能體的選擇映射為獎勵。例如，如果兩個智能體合作，他們每個得到 3 分。如果一個背叛而另一個合作，背叛者得到 5 分，而合作者得到 0 分。如果他們都背叛，每個都會得到 1 分。這些是 Axelrod 在他的比賽中使用的收益。 `play `運行幾輪 PD 游戲。它使用`Agent`類中的以下方法： + `reset`：在第一輪之前初始化智能體，重置他們的分數和他們的回應的歷史記錄。 + `respond`：考慮到對手之前的回應，向每個智能體詢問回應。 + `append`：通過存儲選項，并將連續輪次的分數相加，來更新每個智能體。 在給定的回合數之后，`play`將返回每個智能體的總分數。我選擇了`num_rounds = 6`，以便每個基因型的元素都以大致相同的頻率訪問。第一個元素僅在第一輪訪問，或在六分之一的時間內訪問。接下來的兩個元素只能在第二輪中訪問，或者每個十二分之一。最后四個元素在六分之一時間內訪問，平均每次訪問六次，或者平均每個六分之一。 `Tournament`提供了第二種方法，即`melee`，確定哪些智能體互相競爭： ```py def melee(self, agents, randomize=True): if randomize: agents = np.random.permutation(agents) n = len(agents) i_row = np.arange(n) j_row = (i_row + 1) % n totals = np.zeros(n) for i, j in zip(i_row, j_row): agent1, agent2 = agents[i], agents[j] score1, score2 = self.play(agent1, agent2) totals[i] += score1 totals[j] += score2 for i in i_row: agents[i].fitness = totals[i] / self.num_rounds / 2 ``` `melee`接受一個智能體列表和一個布爾值`randomize`，它決定了每個智能體每次是否與同一鄰居競爭，或者匹配是否隨機化。 `i_row`和`j_row`包含匹配的索引。 `totals`包含每個智能體的總分數。 在循環內部，我們選擇兩個智能體，調用`play`和更新`totals`。 最后，我們計算每個智能體獲得的，每輪和每個對手的平均點數，并將結果存儲在每個智能體的`fitness `屬性中。 ## 12.6 `Simulation` 本章的`Simulation`類基于第？章的中的那個；唯一的區別是`__init__`和`step`。 這是`__init__`方法： ```py class PDSimulation(Simulation): def __init__(self, tournament, agents): self.tournament = tournament self.agents = np.asarray(agents) self.instruments = [] ``` `Simulation`對象包含一個`Tournament`對象，一系列的智能體和一系列的`Instrument`對象（就像第？章中一樣）。 以下是`step`方法： ```py def step(self): self.tournament.melee(self.agents) Simulation.step(self) ``` 此版本的`step`使用`Tournament.melee`，它為每個智能體設置`fitness`屬性；然后它調用父類的`step`方法，父類來自第？章： ```py # class Simulation def step(self): n = len(self.agents) fits = self.get_fitnesses() # see who dies index_dead = self.choose_dead(fits) num_dead = len(index_dead) # replace the dead with copies of the living replacements = self.choose_replacements(num_dead, fits) self.agents[index_dead] = replacements # update any instruments self.update_instruments() ``` `Simulation.step`將智能體的適應性收集到一個數組中; 然后它會調用`choose_dead`來決定哪些智能體死掉，并用`choose_replacements`來決定哪些智能體繁殖。 我的模擬包含生存差異，就像第？章那樣，但不包括繁殖差異。 你可以在本章的筆記本上看到細節。 作為練習之一，你將有機會探索繁殖差異的效果。 ## 12.7 結果 假設我們從三個智能體開始：一個總是合作，一個總是背叛，另一個執行 TFT 策略。 如果我們在這個種群中運行`Tournament.melee`，合作者每輪獲得 1.5 分，TFT 智能體獲得 1.9 分，而背叛者獲得 3.33 分。 這個結果表明，“總是背叛”應該很快成為主導策略。 但是“總是缺陷”包含著自我破壞的種子，如果更好的策略被驅使而滅絕，那么背叛者就沒有人可以利用，他們的適應性下降，并且容易受到合作者的入侵。 根據這一分析，預測系統的行為不容易：它會找到一個穩定的平衡點，還是在基因型景觀的各個位置之間振蕩？ 讓我們運行模擬來發現它！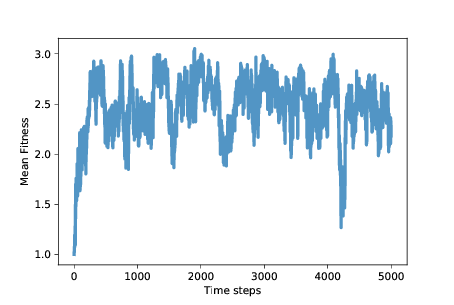 我以 100 個始終背叛的相同智能體開始，并運行 5000 個步驟的模擬： ```py tour = Tournament() agents = make_identical_agents(100, list('DDDDDDD')) sim = PDSimulation(tour, agents) ```  圖 12.1：平均適應性（囚徒困境的每個回合的所得點數） 圖？展示了隨時間變化的平均適應性（使用第？章的`MeanFitness`儀器）。最初平均適應性是 1，因為當背叛者面對對方時，他們每輪只能得到 1 分。 經過大約 500 個時間步，平均適應性增加到近 3，這是合作者面對彼此時得到的。但是，正如我們所懷疑的那樣，這種情況不穩定。在接下來的 500 個步驟中，平均適應性下降到 2 以下，回到 3，并繼續振蕩。 模擬的其余部分變化很大，但除了一次大的下降之外，平均適應性通常在 2 到 3 之間，長期平均值接近 2.5。 而且這還不錯！它不是一個合作的烏托邦，每輪平均得 3 分，但距離始終背叛的烏托邦還很遠。這比我們所期待的，自利智能體的自然選擇要好得多。 為了深入了解這種適應性水平，我們來看看更多的儀器。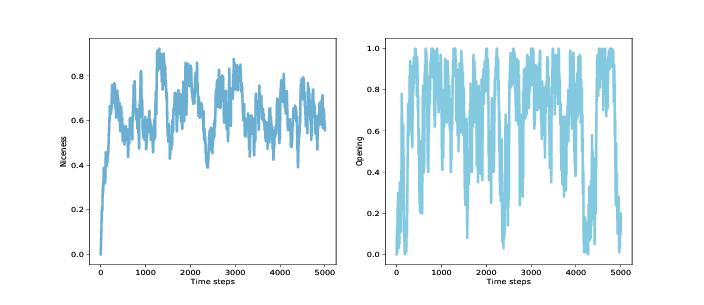`Niceness`在每個時間步驟之后測量智能體的基因型的合作比例： ```py class Niceness(Instrument): def update(self, sim): responses = np.array([agent.values for agent in sim.agents]) metric = np.mean(responses == 'C') self.metrics.append(metric) ```  圖 12.2：種群中所有基因組的平均友善度（左）和第一輪合作的種群比例（右） 圖？（左圖）展示結果：平均友善度從 0 迅速上升到 0.75，然后在 0.4 到 0.85 之間波動，長期平均值接近 0.65。 同樣，這相當好！ 具體看開始的移動，我們可以追蹤第一輪合作的智能體的比例。 這是這個儀器： ```py class Retaliating(Instrument): def update(self, sim): after_d = np.array([agent.values[2::2] for agent in sim.agents]) after_c = np.array([agent.values[1::2] for agent in sim.agents]) metric = np.mean(after_d=='D') - np.mean(after_c=='D') self.metrics.append(metric) ``` 報復行為將所有基因組中的元素數量，其中對手背叛后智能體也背叛（元素 2, 4 和 6），與其中的元素數量，其中對手合作后智能體背叛相比較。正如你現在的預期，結果差異很大（你可以在筆記本中看到圖形）。平均而言，這些分數之間的差異小于 0.1，所以如果智能體在對手合作后，30% 的時間中背叛，他們可能會在背叛后的 40% 時間中背叛。 這個結果為這個斷言提供了較弱的支持，即成功的策略會報復。也許所有智能體甚至很多智能體都沒有必要進行報復；如果整個種群中至少存在一定的報復傾向，那么這可能足以阻止高度報復策略的普及。 為了衡量寬恕，我再次定義了一個工具，來查看在前兩輪之后，智能體是否更有可能在 D-C 之后進行合作，與 C-D 相比。在我的模擬中，沒有證據表明這種特殊的寬恕。另一方面，這些模擬中的策略在某種意義上是必然的寬容，因為它們只考慮前兩輪的歷史。 ## 12.8 總結 Axelrod 的比賽提出了解決利他主義問題的一個可能的解決辦法：或許善良，但不是太善良，是適應性的。但是原始比如中的策略是由人們，而不是進化論設計的，并且策略的分布在比賽過程中沒有改變。 所以這就提出了一個問題：像 TFT 這樣的策略可能會在固定的人為設計策略中表現良好，但它們是否會進化？換句話說，他們是否可以通過變異出現在種群中，與祖先競爭成功，并抵抗他們的后代的入侵？ 本章中的模擬表明： + 背叛者種群容易受到更善良的策略的入侵。 + 過于善良的種群容易受到背叛者的入侵。 + 所以，善良的平均程度有所波動，但善良的平均數量普遍較高，而平均適應程度一般更接近合作烏托邦而不是偏差異議程度。 + 在 Alexrod 的比賽中，TFT 是一項成功的戰略，但對于不斷發展的種群來說，這似乎不是一個最佳策略。事實上，可能沒有穩定的最佳策略。 + 某種程度的報復可能是適應性的，但對所有智能體來說，可能沒有必要進行報復。 如果在整個種群中有足夠的報復行為，這可能足以防止背叛者入侵 [4]。 > [4] 這就引入了博弈論中一個全新的話題 - 搭便車問題（見 <https://en.wikipedia.org/wiki/Free-rider_problem>）。 很明顯，這些模擬中的智能體很簡單，而囚徒困境是一種有限范圍的社交互動的高度抽象模型。 盡管如此，本章的結果對人性提供了一些見解。 也許我們對合作，報復和寬恕的傾向是天生的，至少部分是。 這些特征是我們的大腦的工作機制的結果，至少部分是由我們的基因控制的。 也許我們的基因這樣來構建我們的大腦，因為在人類進化史上，自私的大腦的基因不太可能傳播。 所以也許這就是為什么自私基因會建立無私的大腦。 ## 12.9 練習 本章的代碼位于本書倉庫的 Jupyter 筆記本`chap12.ipynb`中。打開筆記本，閱讀代碼并運行單元個。你可以使用這個筆記本來練習本章的練習。我的解決方案在`chap12soln.ipynb`中。 練習 1 本章中的模擬取決于我任意選擇的條件和參數。作為練習，我鼓勵你去探索其他條件，看看他們對結果有什么影響。這里有一些建議： 1. 改變初始條件：不要從所有背叛者開始，看看如果從所有合作者，所有 TFT 或隨機智能體開始會發生什么。 1. 在`Tournament.melee`中，我在每個時間步驟開始時洗牌，所以每個玩家對抗兩個隨機選擇的玩家。如果你不洗牌會怎么樣？在這種情況下，每個智能體都會反復與相同的鄰居進行比賽。這可能會讓少數人的戰略，更容易通過利用局部性入侵大多數。 1. 由于每個智能體只與另外兩個智能體進行比賽，因此每輪比賽的結果都是非常不同的：在任何一輪比賽中，勝過大部??分智能體的智能體可能會運氣不好，或者相反。如果增加每個智能體在每輪中的對手數量會發生什么？或者如果在每一步結束時，智能體的適應性是上一輪結束時其當前得分和適應性的平均值，會怎么樣？ 1. 我為`prob_survival`函數選擇的值從 0.7 到 0.9 不等，所以適應性最差的智能體`p = 0.7`，生存了 3.33 個時間步驟，適應性最強的智能體生存了 10 個。如果你使`prob_survival`更加或更加不“激進”，會發生什么情況。 1. 我選擇了`num_rounds = 6`，以便基因組的每個元素對比賽的結果具有大致相同的影響。 但這比 Alexrod 在他的比賽中使用的值要小得多。 如果增加`num_rounds`會發生什么？ 注意：如果你研究這個參數的效果，你可能想修改`Niceness`來衡量基因組中最后4個元素的友善度，隨著`num_rounds`的增加，它會受到更多的選擇性壓力。 1. 我的實現擁有生存差異和隨機繁殖。 如果添加繁殖差異會發生什么？ 練習 2 在我的模擬中，種群從未收斂到一個狀態，其中多數人共享相同的，據推測是最佳的基因型。對于這個結果有兩種可能的解釋：一是沒有最佳策略，因為無論何時種群被大多數基因型控制，這種狀況為少數人入侵提供了機會；另一種可能性是，突變率高到足以維持多種基因型，即使多數是非最佳的。為了辨別這些解釋，請嘗試降低突變率來查看發生了什么。或者，從隨機種群開始，并且不帶突變來運行，直到只有一個基因型存活。或者帶突變來運行，直到系統達到穩定狀態；然后關閉突變并運行，直到只有一個幸存的基因型。這些情況下基因型的特征是什么？ 練習 3 我的實驗中的智能體是“反應型”的，因為他們在每輪中的選擇只取決于對手在前幾輪中的做法。考慮探索一些策略，它們也考慮到智能體過去的選擇。這樣的策略將能夠區分報復性對手，和沒有挑釁而背叛的對手。