附錄 A、算法分析 · 復雜性思維中文第二版

# 附錄 A、算法分析 > 原文：[Appendix A Analysis of algorithms](http://greenteapress.com/complexity2/html/thinkcomplexity2014.html) > 譯者：[飛龍](https://github.com/wizardforcel) > 協議：[CC BY-NC-SA 4.0](http://creativecommons.org/licenses/by-nc-sa/4.0/) > 自豪地采用[谷歌翻譯](https://translate.google.cn/) > 部分參考了[《Think Python 2e 中譯本第二十一章：算法分析》](http://codingpy.com/books/thinkpython2/21-analysis-of-algorithms.html) _算法分析_ (**Analysis of algorithms**) 是計算機科學的一個分支，著重研究算法的性能，特別是它們的運行時間和資源開銷。見 [http://en.wikipedia.org/wiki/Analysis_ofalgorithms](http://en.wikipedia.org/wiki/Analysis_ofalgorithms) 。算法分析的實際目的是預測不同算法的性能，用于指導設計決策。 2008年美國總統大選期間，當候選人奧巴馬(Barack Obama)訪問Google時，他被要求進行即時分析。首席執行官 Eric Schmidt 開玩笑地問他“對一百萬個32位整數排序的最有效的方法”。顯然有人暗中通知了奧巴馬，因為他很快回答，“我認為不應該采用冒泡排序法”。詳見 [http://www.youtube.com/watch?v=k4RRi_ntQc8](http://www.youtube.com/watch?v=k4RRi_ntQc8) 。是真的：冒泡排序概念上很簡單，但是對于大數據集來說速度非常慢。Schmidt所提問題的答案可能是 “基數排序 ([http://en.wikipedia.org/wiki/Radix_sort](http://en.wikipedia.org/wiki/Radix_sort))” [1]。 > [1] 但是，如果你面試中被問到這個問題，我認為更好的答案是，“對上百萬個整數進行最快排序的方法就是用你所使用的語言的內建排序函數。它的性能對于大多數應用而言已優化的足夠好。但如果最終我的應用運行太慢，我會用性能分析器找出大量的運算時間被用在了哪兒。如果采用一個更快的算法會對性能產生顯著的提升，我會試著找一個基數排序的優質實現。” 算法分析的目的是在不同算法間進行有意義的比較，但是有一些問題： * 算法的相對性能依賴于硬件的特性，因此一個算法可能在機器A上比較快，另一個算法則在機器B上比較快。對此問題一般的解決辦法是指定一個 _機器模型_ (machine model) 并且分析一個算法在一個給定模型下所需的步驟或運算的數目。 * 相對性能可能依賴于數據集的細節。例如，如果數據已經部分排好序，一些排序算法可能更快；此時其它算法運行的比較慢。避免該問題的一般方法是分析 _最壞情況_。有時分析平均情況性能也可，但那通常更難，而且可能不容易弄清該對哪些數據集合進行平均。 * 相對性能也依賴于問題的規模。一個對于小列表很快的排序算法可能對于長列表很慢。此問題通常的解決方法是將運行時間（或者運算的次數）表示成問題規模的函數，并且根據各自隨著問題規模的增長而增加的速度，將函數分成不同的類別。此類比較的好處是有助于對算法進行簡單的分類。例如，如果我知道算法A的運行時間與輸入的規模 `n` 成正比，算法 B 與 `n^2` 成正比，那么我可以認為 A 比 B 快，至少對于很大的 `n` 值來說。這類分析也有一些問題，我們后面會提到。 ## A.1 增長級別假設你已經分析了兩個算法，并能用輸入計算量的規模表示它們的運行時間：若算法 A 用 `100n+1` 步解決一個規模為 `n` 的問題；而算法 B 用 `n^2 + n + 1` 步。下表列出了這些算法對于不同問題規模的運行時間： | 輸入大小 | 算法 A 的運行時間 | 算法 B 的運行時 | | --- | --- | --- | | 10 | 1,001 | 111 | | 100 | 10,001 | 10,101 | | 1,000 | 100,001 | 1,001,001 | | 10,000 | 1,000,001 | `> 10^10` | 當 `n=10` 時，算法 A 看上去很糟糕，它用了 10 倍于算法 B 所需的時間。但當 `n=100` 時，它們性能幾乎相同，而 `n` 取更大值時，算法 A 要好得多。根本原因是對于較大的 `n` 值，任何包含 `n^2` 項的函數都比首項為 `n` 的函數增長要快。 _首項_ (leading term) 是指具有最高指數的項。對于算法A，首項有一個較大的系數 100，這是為什么對于小 `n` ，B比A好。但是不考慮該系數，總有一些 `n` 值使得 `a n^2 > b n`，`a` 和 `b` 可取任意值。同樣推論也適用于非首項。即使算法 A 的運行時間為 `n+1000000` ，對于足夠大的 `n` ，它仍然比算法 B 好。一般來講，我們認為具備較小首項的算法對于規模大的問題是一個好算法，但是對于規模小的問題，可能存在有一個 _交叉點_ (crossover point)，在此規模以下，另一個算法更好。交叉點的位置取決于算法的細節、輸入以及硬件，因此在進行算法分析時它通常被忽略。但是這不意味著你可以忘記它。如果兩個算法有相同的首項，很難說哪個更好；答案還是取決于細節。所以對于算法分析來說，具有相同首項的函數被認為是相當的，即使它們具有不同的系數。 _增長級別_(order of growth)是一個函數集合，集合中函數的增長行為被認為是相當的。例如`2n`、`100n`和`n+1`屬于相同的增長級別，可用 _大O符號_(Big-Oh notation) 寫成`O(n)`，而且常被稱作 _線性級_ (linear)，因為集合中的每個函數隨著`n`線性增長。首項為 `n^2` 的函數屬于 `O(n^2)`；它們被稱為 _二次方級_ (quadratic)。下表列出了算法分析中最通常的一些增長級別，按照運行效率從高到低排列。 | 增長級別 | 名稱 | | --- | --- | | `O(1)` | 常數 | | `O(logn)` | 對數 | | `O(n)` | 線性 | | `O(n logn)` | 線性對數 | | `O(n^2)` | 二次 | | `O(n^3)` | 三次 | | `O(c^n)` | 指數 | 對于對數級，對數的基數并不影響增長級別。改變基數等價于乘以一個常數，其不改變增長級別。相應的，所有的指數級數都屬于相同的增長級別，而無需考慮指數的基數大小。指數函數增長級別增長的非常快，因此指數級算法只用于小規模問題。練習 1 訪問 [http://en.wikipedia.org/wiki/Big_O_notation](http://en.wikipedia.org/wiki/Big_O_notation) ，閱讀維基百科關于大O符號的介紹，并回答以下問題： 1. `n^3 + n^2`的增長級別是多少？`1000000 n^3 + n^2` 和 `n^3 + 1000000 n^2` 的增長級別又是多少？ 2. `(n^2 + n) * (n + 1)`的增長級別是多少？在開始計算之前，記住你只需要考慮首項即可。 3. 如果 `f` 的增長級別為 `O(g)` ，那么對于未指定的函數 `g` ，我們可以如何描述 `af+b` ？ 4. 如果 `f1` 和 `f2` 的增長級別為 `O(g)`，那么 `f1 + f2` 的增長級別又是多少？ 5. 如果 `f1` 的增長級別為 `O(g)` ，`f2` 的增長級別為 `O(h)`，那么 `f1 + f2` 的增長級別是多少？ 6. 如果 `f1` 的增長級別為 `O(g)` ，`f2` 的增長級別為 `O(h)`，那么 `f1 * f2` 的增長級別是多少？關注性能的程序員經常發現這種分析很難忍受。他們的觀點有一定道理：有時系數和非首項會產生巨大的影響。有時，硬件的細節、編程語言以及輸入的特性會造成很大的影響。對于小問題，漸近的行為沒有什么影響。但是，如果你牢記這些注意事項，算法分析就是一個有用的工具。至少對于大問題，“更好的” 算法通常更好，并且有時要好的多。相同增長級別的兩個算法之間的不同通常是一個常數因子，但是一個好算法和一個壞算法之間的不同是無限的！ ## A.2 Python基本運算操作分析在 Python 中，大部分算術運算的開銷是常數級的；乘法會比加減法用更長的時間，除法更長，但是這些運算時間不依賴被運算數的數量級。非常大的整數卻是個例外；在這種情況下，運行時間隨著位數的增加而增加。索引操作 — 在序列或字典中讀寫元素 — 的增長級別也是常數級的，和數據結構的大小無關。一個遍歷序列或字典的 for 循環通常是線性的，只要循環體內的運算是常數時間。例如，累加一個列表的元素是線性的： ```py total = 0 for x in t: total += x ``` 內建函數 `sum` 也是線性的，因為它做的是相同的事情，但是它要更快一些，因為它是一個更有效的實現；從算法分析角度講，它具有更小的首項系數。根據經驗，如果循環體內的增長級別是 `O(n^a)`，則整個循環的增長級別是`O(n^(a+1))`。如果這個循環在執行一定數目循環后退出則是例外。無論 `n` 取值多少，如果循環僅執行 `k` 次，整個循環的增長級別是`O(n^a)`，即便 `k` 值比較大。乘上 `k` 并不會改變增長級別，除法也是。因此，如果循環體的增長級別是 `O(n^a)`，而且循環執行 `n/k` 次，那么整個循環的增長級別就是 `O(n^(a+1))` , 即使 `k` 值很大。大部分字符串和元組運算是線性的，除了索引和 `len` ，它們是常數時間。內建函數 `min` 和 `max` 是線性的。切片運算與輸出的長度成正比，但是和輸入的大小無關。字符串拼接是線性的；它的運算時間取決于運算對象的總長度。所有字符串方法都是線性的，但是如果字符串的長度受限于一個常數 — 例如，在單個字符上的運算 — 它們被認為是常數時間。字符串方法 `join` 也是線性的；它的運算時間取決于字符串的總長度。大部分的列表方法是線性的，但是有一些例外： * 平均來講，在列表結尾增加一個元素是常數時間。當它超出了所占用空間時，它偶爾被拷貝到一個更大的地方，但是對于 `n` 個運算的整體時間仍為 `O(n)` ，所以我每個運算的平均時間是 `O(1)` 。 * 從一個列表結尾刪除一個元素是常數時間。 * 排序是 `O(n logn)` 。大部分的字典運算和方法是常數時間，但有些例外： * `update` 的運行時間與作為形參被傳遞的字典（不是被更新的字典）的大小成正比。 * `keys`、`values` 和 `items` 是常數時間，因為它們返回迭代器。但是如果你對迭代器進行循環，循環將是線性的。字典的性能是計算機科學的一個小奇跡之一。在[哈希表](#hashtable)一節中，我們將介紹它們是如何工作的。練習 2 訪問 [http://en.wikipedia.org/wiki/Sorting_algorithm](http://en.wikipedia.org/wiki/Sorting_algorithm) ，閱讀維基百科上對排序算法的介紹，并回答下面的問題： 1. 什么是“比較排序”？比較排序在最差情況下的最好增長級別是多少？別的排序算法在最差情況下的最優增長級別又是多少？ 2. 冒泡排序法的增長級別是多少？為什么奧巴馬認為是“不應采用的方法” 3. 基數排序(radix sort)的增長級別是多少？我們使用它之前需要具備的前提條件有哪些？ 4. 排序算法的穩定性是指什么？為什么它在實際操作中很重要？ 5. 最差的排序算法是哪一個（有名稱的）？ 6. C 語言使用哪種排序算法？Python使用哪種排序算法？這些算法穩定嗎？你可能需要谷歌一下，才能找到這些答案。 7. 大多數非比較算法是線性的，因此為什 Python 使用一個增長級別為 `O(n logn)` 的比較排序？ ## A.3 搜索算法分析 _搜索_ (search)算法，接受一個集合以及一個目標項，并判斷該目標項是否在集合中，通常返回目標的索引值。最簡單的搜素算法是“線性搜索”，其按順序遍歷集合中的項，如果找到目標則停止。最壞的情況下，它不得不遍歷全部集合，所以運行時間是線性的。序列的 in 操作符使用線性搜索；字符串方法 `find` 和 `count` 也使用線性搜索。如果元素在序列中是排序好的，你可以用 _二分搜素_ (bisection search) ，它的增長級別是 `O(logn)` 。二分搜索和你在字典中查找一個單詞的算法類似（這里是指真正的字典，不是數據結構）。你不會從頭開始并按順序檢查每個項，而是從中間的項開始并檢查你要查找的單詞在前面還是后面。如果它出現在前面，那么你搜索序列的前半部分。否則你搜索后一半。如論如何，你將剩余的項數分為一半。練習 3 編寫一個叫做`bisection`的函數，它接受有序列表和目標值，并返回列表中值的索引（如果存在的話）；如果不存在則返回`None`。或者你可以閱讀對分模塊的文檔并使用它！如果序列有 1,000,000 項，它將花 20 步找到該單詞或判斷出其不在序列中。因此它比線性搜索快大概 50,000 倍。二分搜索比線性搜索快很多，但是它要求已排序的序列，因此使用時需要做額外的工作。另一個檢索速度更快的數據結構被稱為 _哈希表_ (hashtable) — 它可以在常數時間內檢索出結果 — 并且不依賴于序列是否已排序。 Python 中的字典就通過哈希表技術實現的，因此大多數的字典操作，包括 in 操作符，只花費常數時間就可完成。 ## A.4 哈希表為了解釋哈希表是如何工作以及為什么它的性能如此優秀，我們從實現一個簡單的映射(map)開始并逐步改進它，直到其成為一個哈希表。我們使用 Python 來演示這些實現，但在現實生活中，你用不著用 Python 寫這樣的代碼；你只需用內建的字典對象就可以了！因此在接下來的內容中，你就當字典對象并不存在，你希望自己實現一個將鍵映射到值的數據結構。你必須實現的操作包括： `add(k, v)`： > 增加一個新的項，其從鍵 k 映射到值 v 。如果使用 Python 的字典d，該運算被寫作 `d[k] = v`。 `get(k)`： > 查找并返回相應鍵的值。如果使用 Python 的字典d，該運算被寫作 `d[k]` 或 `d.get(k)` 。現在，假設每個鍵只出現一次。該接口最簡單的實現是使用一個元組列表，其中每個元組是一個鍵-值對。 ```py class LinearMap: def __init__(self): self.items = [] def add(self, k, v): self.items.append((k, v)) def get(self, k): for key, val in self.items: if key == k: return val raise KeyError ``` `add` 向項列表追加一個鍵—值元組，其增長級別為常數時間。 `get` 使用 `for` 循環搜索該列表：如果它找到目標鍵，則返回相應的值；否則觸發一個 `KeyError`。因此 `get` 是線性的。另一個方案是保持列表按鍵排序。那么，`get` 可以使用二分搜索，其增長級別為 `O(logn)` 。但是在列表中間插入一個新的項是線性的，因此這可能不是最好的選擇。有其它的數據結構能在對數級時間內實現 `add` 和 `get` ，但是這仍然不如常數時間好，那么我們繼續。另一種改良 `LinearMap` 的方法是將鍵-值對列表分成小列表。下面是一個被稱作 `BetterMap` 的實現，它是 100 個 `LinearMap` 組成的列表。正如一會兒我們將看到的，`get` 的增長級別仍然是線性的，但是 `BetterMap` 是邁向哈希表的一步。 ```py class BetterMap: def __init__(self, n=100): self.maps = [] for i in range(n): self.maps.append(LinearMap()) def find_map(self, k): index = hash(k) % len(self.maps) return self.maps[index] def add(self, k, v): m = self.find_map(k) m.add(k, v) def get(self, k): m = self.find_map(k) return m.get(k) ``` `__init__`會生成一個由 n 個 `LinearMap` 組成的列表。 `add`和 `get` 使用 `find_map` 查找往哪一個列表中添加新項，或者對哪個列表進行檢索。 `find_map` 使用了內建函數 `hash`，其接受幾乎任何 Python 對象并返回一個整數。這一實現的一個限制是它僅適用于可哈希的鍵。像列表和字典等可變類型是不能哈希的。被認為是相等的可哈希對象返回相同的哈希值，但是反之不是必然成立：兩個具備不同值的對象能夠返回相同的哈希值。 `find_map`使用求余運算符將哈希值包在 0 到 `len(self.maps)` 之間，因此結果是該列表的合法索引值。當然，這意味著許多不同的哈希值將被包成相同的索引值。但是如果哈希函數散布相當均勻（這是哈希函數被設計的初衷），那么我們預計每個 `LinearMap` 會有 `n/100` 項。由于 `LinearMap.get` 的運行時間與項數成正比，那么我們預計 `BetterMap` 比 `LinearMap` 快100倍。增長級別仍然是線性的，但是首項系數變小了。這樣很好，但是仍然不如哈希表好。下面是使哈希表變快的關鍵：如果你能保證 `LinearMap` 的最大長度是有上限的，則 `LinearMap.get` 的增長級別是常數時間。你只需要跟蹤項數并且當每個 `LinearMap` 的項數超過閾值時，通過增加更多的 `LinearMap` 調整哈希表的大小。以下是哈希表的一個實現： ```py class HashMap: def __init__(self): self.maps = BetterMap(2) self.num = 0 def get(self, k): return self.maps.get(k) def add(self, k, v): if self.num == len(self.maps.maps): self.resize() self.maps.add(k, v) self.num += 1 def resize(self): new_maps = BetterMap(self.num * 2) for m in self.maps.maps: for k, v in m.items: new_maps.add(k, v) self.maps = new_maps ``` 每個 `HashMap` 包含一個 `BetterMap`。`__init__` 開始僅有兩個 `LinearMap` ，并且初始化 `num`，用于跟蹤項的數量。 `get`僅僅用來調度 `BetterMap`。真正的操作發生于 `add` 內，其檢查項的數量以及 `BetterMap` 的大小：如果它們相同，每個 `LinearMap` 的平均項數為 1，因此它調用 `resize`。 `resize` 生成一個新的 `BetterMap`，是之前那個的兩倍大，然后將像從舊表“重新哈希”至到新的表。重新哈希是必要的，因為改變 `LinearMap` 的數目也改變了 `find_map` 中求余運算的分母。這意味著一些被包進相同的 `LinearMap` 的對象將被分離（這正是我們希望的，對吧？）。重新哈希是線性的，因此 `resize` 是線性的，這可能看起來很糟糕，因為我保證 `add` 會是常數時間。但是記住，我們不必每次都調整，因此 `add` 通常是常數時間，只是偶爾是線性的。運行 `add` `n` 次的整體操作量與 `n` 成正比，因此 `add` 的平均運行時間是常數時間！為了弄清這是如何工作的，考慮以一個空的 `HashTable` 開始并增加一系列項。我們以兩個 `LinearMap` 開始，因此前兩個 `add` 操作很快（不需要調整大小）。我們假設它們每個操作花費一個工作單元。下一個 `add` 需要進行一次大小調整，因此我們必須重新哈希前兩項（我們將其算成兩個額外的工作單元），然后增加第3項（又一個工作單元）。增加下一項的花費一個單元，所以目前為止添加四個項共需要 6 個單元。下一個 `add` 花費 5 個單元，但是之后的3個操作每個只花費 1 個單元，所以前八個 `add` 總共需要 14 個單元。下一個 `add` 花費 9 個單元，但是之后在下一次調整大小之前，可以再增加七個，所以前 16 個 `add` 總共需要 30 個單元。進行 32 次 `add` 之后，總共花費了 62 個單元，我希望你開始看到規律。 `n`次 `add` 后，其中 `n` 是 2 的倍數，總花費是 `2n-2` 個單元，所以平均每個 `add` 操作只花費了少于 2 個單元。當 `n` 是 2 的倍數時，那是最好的情況。對于其它的 `n` 值，平均花費稍高一點，但是那并不重要。重要的是其增長級別為 `O(1)` 。下圖形象地說明了其工作原理。每個區塊代表一個工作單元。每列顯示每個 `add` 所需的單元，按從左到右的順序排列：前兩個 `add` 花費 1 個單元，第三個花費 3 個單元，等等。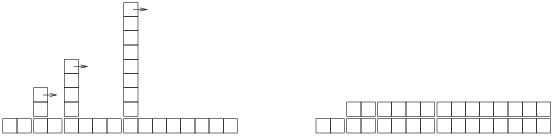 ![](https://img.kancloud.cn/12/5e/125e89808c4a97b539a29fd32bff2c89_553x136.png) 圖 A.1：哈希表中 `add` 操作的成本重新哈希的額外工作，表現為一系列不斷增高的高塔，各自之間的距離越來越大。現在，如果你打翻這些塔，將大小調整的代價均攤到所有的 `add` 上，你會從圖上看到 `n` 次 `add` 的整個花費是 `2n - 2` 。該算法一個重要的特征是，當我們調整 `HashTable` 的大小時，它呈幾何級增長；也就是說，我們用常數乘以表的大小。如果你按算術級增加大小 —— 每次增加固定的數目 —— 每個 `add` 的平均時間是線性的。你可以從 [http://thinkpython2.com/code/Map.py](http://thinkpython2.com/code/Map.py) 下載到 `HashMap` 的實現代碼，你不必使用它；如果你想要一個映射數據結構，只要使用 Python 中的字典即可。練習 4 我的`HashMap`實現直接訪問`BetterMap`的屬性，這表現了糟糕的面向對象設計。 + 特殊方法`__len__`由內置函數`len`調用。為`BetterMap`編寫一個`__len__`方法并在`add`中使用它。 + 使用生成器來編寫`BetterMap.iteritems`，并在`resize`中使用它。練習 5 散列表的一個缺點是元素必須是可散列的，這通常意味著它們必須是不可變的。這就是為什么在 Python 中，可以將元組而不是列表用作字典中的鍵。另一種方法是使用基于樹的映射。編寫一個名為`TreeMap`的映射接口的實現，它使用紅黑樹，以對數時間執行`add `和`log`。 ## A.5 列表的求和假設你有一堆列表，并且你想把它們合并成一個列表。有三種方法可以在 Python 中執行此操作：你可以使用`+=`運算符： ```py total = [] for x in t: total += x ``` 或者`extend `方法： ```py total = [] for x in t: total.extend(x) ``` 或者內建的`sum`函數： ```py total = sum(t, []) ``` `sum`的第二個參數是總數的初始值。在不知道如何實現`+=`和`extend `和`sum`的情況下，很難分析它們的性能。例如，如果`total += x`每次創建一個新列表，則循環是二次的；但如果它修改了總數，它是線性的。為了找到答案，我們可以閱讀源代碼，但作為練習，讓我們看看我們是否可以通過測量運行時間來弄清楚它。測量程序運行時間的簡單方法，是使用`os`模塊中的`time`函數，該函數返回浮點數的元組，表示進程已經過的時間（詳細信息請參閱文檔）。我使用了函數`etime`，它返回“用戶時間”和“系統時間”的總和，這通常是我們關心的性能度量： ```py import os def etime(): """See how much user and system time this process has used so far and return the sum.""" user, sys, chuser, chsys, real = os.times() return user+sys ``` 為了衡量一個函數的運行時間，你可以調用`etime`兩次并計算差異： ```py start = etime() # put the code you want to measure here end = etime() elapsed = end - start ``` 或者，如果你使用 IPython，則可以使用`timeit`命令。請參閱`ipython.scipy.org`。如果算法是二次的，我們期望運行時間`t`與輸入大小`n`的函數，是這樣的： ``` t = a * n^2 + b * n + c ``` 其中`a`，`b`和`c`是未知系數。如果你對兩邊取對數，你會得到： ``` logt ~ loga + 2logn ``` 對于`n`的較大值，非主要項是微不足道的，并且這個近似值非常好。所以如果我們在雙對數刻度上繪制`t`對`n`，我們期待斜率為 2 的直線。類似地，如果算法是線性的，我們期望斜率為 1 的直線。我寫了三個連接列表的函數：`sum_plus`使用`+=`；`sum_extend`使用`list.extend`；`sum_sum`使用`sum`。我在`n`的范圍內對它們計時，并將結果繪制在雙對數刻度上。下圖展示了結果。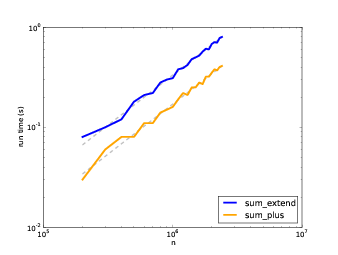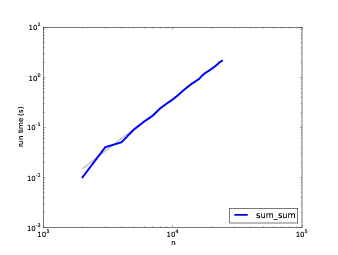 ![](https://img.kancloud.cn/23/e3/23e3ba9af16ad322585b339cab91d3a1_338x255.png) 圖 a.2：運行時間和`n`，虛線斜率為 1 ![](https://img.kancloud.cn/b8/e7/b8e7f4c0cf7163294287b6c7ef6ddf23_338x255.png) 圖 a.3：運行時間和`n`，虛線斜率為 2 在圖 a.2 中，我用斜率為 1 的直線擬合了曲線。這條線很好地擬合了數據，所以我們得出結論，這些實現是線性的。 `+=`實現的速度比較快，因為每次循環中，查找`extend`方法需要一些時間。在圖 a.3 中，斜率 2 的線擬合了數據，所以`sum`實現是二次的。 ## A.6 `pyplot` 為了制作本節中的圖片，我使用了`pyplot`，它是`matplotlib`的一部分。如果你的 Python 安裝沒有帶著`matplotlib`，你可能需要安裝它，或者你可以使用另一個庫進行繪圖。下面是一個簡單的例子： ```py import matplotlib.pyplot as pyplot pyplot.plot(xs, ys) scale = 'log' pyplot.xscale(scale) pyplot.yscale(scale) pyplot.title('') pyplot.xlabel('n') pyplot.ylabel('run time (s)') pyplot.show() ``` 導入語句使`matplotlib.pyplot`可以使用較短的名稱`pyplot`訪問。 `plot `接受`x`值列表和一個`y`值列表并繪制它們。列表的長度必須相同。 `xscale`和`yscale`設置線性或對數軸。 `title`，`xlabel`和`ylabel`是不言自明的。最后，`show`在屏幕上顯示該圖。你也可以使用`savefig`將繪圖保存在文件中。 `pyplot`的文檔位于 <http://matplotlib.sourceforge.net/>。練習 6 測試`LinearMap`，`BetterMap`和`HashMap`的性能；看看你能否描述它們的增長級別。你可以從`thinkcomplex.com/Map.py`下載我的映射實現，以及從`thinkcomplex.com/listsum.py`下載我在本節中使用的代碼。你必須找到一個`n`的范圍，它大到足以顯示漸近行為，但小到足以快速運行。