# 九、基于智能體的模型 > 原文：[Chapter 9 Agent-based models](http://greenteapress.com/complexity2/html/thinkcomplexity2010.html) > 譯者：[飛龍](https://github.com/wizardforcel) > 協議：[CC BY-NC-SA 4.0](http://creativecommons.org/licenses/by-nc-sa/4.0/) > 自豪地采用[谷歌翻譯](https://translate.google.cn/) 我們迄今為止看到的模型可能具有“基于規則”的特征，因為它們涉及受簡單規則支配的系統。 在本章和以后的章節中，我們將探索基于智能體（agent）的模型。 基于智能體的模型包含智能體，它旨在模擬人和其他實體，它們收集世界的信息，制定決策并采取行動。 智能體通常位于空間或網絡中，并在本地彼此交互。 他們通常有不完整的，不全面的世界信息。 智能體之間經常存在差異，而不像以前的所有模型，它們的所有成分都相同。 基于智能體的模型通常包含智能體之間，或世界中的隨機性。 自 20 世紀 70 年代以來，基于智能體的模型已成為經濟學和其他社會科學，以及一些自然科學中的重要工具。 基于智能體的模型對非均衡系統的動態建模（盡管它們也用于研究均衡系統）非常有用。 它們對于理解個人決策和系統行為之間的關系特別有用。 本章的代碼位于`chap09.ipynb`中，它是本書倉庫中的 Jupyter 筆記本。 使用此代碼的更多信息，請參見第？節。 ## 9.1 謝林模型 1971 年，托馬斯謝（Thomas Schelling）發表了《隔離的動態模型》（Dynamic Models of Segregation），該模型提出了種族隔離的簡單模型。 謝林模型的世界是一個網格；每個細胞代表一棟房子。 房屋被兩種智能體占用，標記為紅色和藍色，數量大致相同。 大約 10% 的房屋是空的。 在任何時候，智能體可能會高興或不高興，這取決于領域中的其他智能體，每個房屋的“鄰居”是八個相鄰細胞的集合。在一個版本的模型中，如果智能體至少有兩個像他們一樣的鄰居，智能體會高興，但如果是一個或零，他們就會不高興。 模擬的過程是，隨機選擇一個智能體并檢查他們是否高興。 如果是這樣，沒有任何事情發生。如果不是，智能體隨機選擇其中一個未占用的細胞并移動。 聽到這種模型導致一些隔離，你可能不會感到驚訝，但是你可能會對這個程度感到驚訝。 很快，會出現相似智能體的群落。 隨著時間的推移，這些群落會不斷聚合，直到有少量的大型群落，并且大多數智能體生活在同質社區中。 如果你不知道這個過程，只看到結果，你可能會認為智能體是種族主義者，但實際上他們都會在一個混合的社區感到非常高興。 由于他們不愿意數量過大，所以在最壞的情況下，他們可能被認為是排外的。 當然，這些智能體是真實人物的過度簡化，所以這些描述可能根本不恰當。 種族主義是一個復雜的人類問題; 很難想象這樣簡單的模型可以揭示它。 但實際上，它提供了一個強有力論據，有關系統及其各部分之間關系的：如果你觀察真實城市的隔離，你不能總結為，個人的種族主義是直接原因，或者，城市居民是種族主義者。 當然，我們必須牢記這個論述的局限性：謝林模型證明了隔離的一個可能原因，但沒有提到實際原因。 ## 9.2 謝林模型的實現 為了實現謝林模型，我編寫了另一個繼承`Cell2D`的類： ```py class Schelling(Cell2D): def __init__(self, n, m=None, p=0.5): self.p = p m = n if m is None else m choices = [0, 1, 2] probs = [0.1, 0.45, 0.45] self.array = np.random.choice(choices, (n, m), p=probs) ``` 參數`n`和`m`是網格的維度，`p`是相似鄰居比例的閾值。 例如，如果`p = 0.5`，也就是其鄰居中少于 50% 為相同顏色，則智能體將不高興。 `array`是 NumPy 數組，其中每個細胞如果為空，則為 0；如果由紅色智能體占用，則為1；如果由藍色智能體占用，則為 2。 最初，10% 的細胞是空的，45% 為紅色和 45% 為藍色。 謝林模型的`step`函數比以前的`step`函數復雜得多。 如果你對細節不感興趣，你可以跳到下一節。 但是如果你堅持要看，你可能需要一些 NumPy 的提示。 首先，我將生成邏輯數組，表明哪些細胞是紅色，藍色和占用的： ```py a = self.array red = a==1 blue = a==2 occupied = a!=0 ``` 我將使用`np.correlate2d`來計算，對于每個細胞，紅色相鄰細胞的數量和被占用的細胞數量。 ```py options = dict(mode='same', boundary='wrap') kernel = np.array([[1, 1, 1], [1, 0, 1], [1, 1, 1]], dtype=np.int8) num_red = correlate2d(red, kernel, **options) num_neighbors = correlate2d(occupied, kernel, **options) ``` 現在對于每個細胞，我們可以計算出紅色的鄰居比例和相同顏色的比例： ```py frac_red = num_red / num_neighbors frac_blue = 1 - frac_red frac_same = np.where(red, frac_red, frac_blue) ``` `frac_red`只是`num_red`和`num_neighbors`的比率，而`frac_blue`是`frac_red`的補。 `frac_same`有點復雜。 函數`np.where`就像逐元素的`if`表達式一樣。 第一個參數是從第二個或第三個參數中選擇元素的條件。 在這種情況下，如果`red`為`True`，`frac_same`獲取`frac_red`的相應元素。 在紅色為`False`的情況下，`frac_same`獲取`frac_blue`的相應元素。 現在我們可以確定不滿意的智能體的位置： ```py unhappy_locs = locs_where(occupied & (frac_same < self.p)) ``` 結果`unhappy_locs`是一個 NumPy 數組，其中每行都是占用的細胞的坐標，其中`frac_same`低于閾值`p`。 `locs_where `是`np.nonzero`的包裝函數： ```py def locs_where(condition): return np.transpose(np.nonzero(condition)) ``` `np.nonzero`接受一個數組并返回所有非零元素的坐標，但結果是兩個元組的形式。 `np.transpose`將結果轉換為更有用的形式，即每行都是坐標對的數組。 同樣，`empty_locs`是一個數組，包含空細胞的坐標： ```py empty_locs = locs_where(a==0) ``` 現在我們到達了模擬的核心。 我們遍歷不高興的智能體并移動它們： ```py for source in unhappy_locs: i = np.random.randint(len(empty_locs)) dest = tuple(empty_locs[i]) a[dest] = a[tuple(source)] a[tuple(source)] = 0 empty_locs[i] = source ``` `i`是一個用來隨機選擇空細胞的索引。 `dest`是一個包含空細胞的坐標的元組。 為了移動智能體，我們將值從`source`復制到`dest`，然后將`source`的值設置為 0（因為它現在是空的）。 最后，我們用`source`替換`empty_locs`中的條目，以便剛剛變為空的細胞可以由下一個智能體選擇。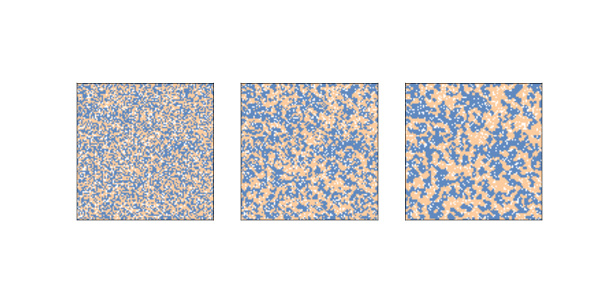 ## 9.3 隔離  圖 9.1：謝林的隔離模型，`n = 100`，初始條件（左），2 步后（中）和 10 步后（右） 現在讓我們看看我們運行模型時會發生什么。 我將以`n = 100`和`p = 0.3`開始，并運行 10 個步驟。 ```py grid = Schelling(n=100, p=0.3) for i in range(10): grid.step() ``` 圖？展示了初始狀態（左），2 步（中）后和 10 步（右）后的模擬。 群落迅速形成，紅色和藍色的智能體移動到隔離集群中，它們由空細胞的邊界分隔。 對于每種狀態，我們可以計算隔離度，它是相同顏色的鄰居的比例。在所有細胞中的平均值： ```py np.sum(frac_same) / np.sum(occupied) ``` 在圖？中，相似鄰居的比例均值在初始狀態中為 55%，兩步后為 71%，10 步后為 80%！ 請記住，當`p = 0.3`時，如果 8 個鄰居中的 3 個是他們自己的顏色，那么智能體會很高興，但他們最終居住在一個社區中，其中 6 或 7 個鄰居是自己的顏色。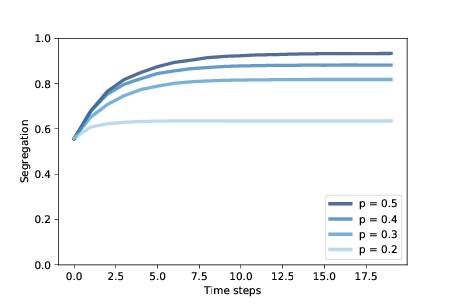  圖 9.2：隨著時間的推移，謝林模型中的隔離程度，范圍為`p` 圖？顯示了隔離程度如何增加，以及它在幾個`p`值下的平穩位置。 當`p = 0.4`時，穩定狀態下的隔離程度約為 88%，且大多數智能體沒有不同顏色的鄰居。 這些結果令許多人感到驚訝，它們成為了個人決策與系統行為之間的，復雜且不可預測的關系的鮮明示例。 ## 9.4 糖域 1996年，約書亞愛潑斯坦（Joshua Epstein）和羅伯特阿克斯特爾（Robert Axtell）提出了糖域（Sugarscape），這是一個“人造社會”的智能體模型，旨在支持經濟學和其他社會科學的相關實驗。 糖域是一款多功能的模型，適用于各種主題。 作為例子，我將復制 Epstein 和 Axtell 的書《Growing Artificial Societies》的前幾個實驗。 糖域最簡單的形式是一個簡單的經濟模型，智能體在二維網格上移動，收集和累積代表經濟財富的“糖”。 網格的一些部分比其他部分產生更多的糖，并且一些智能體比其他人更容易找到它。 這個糖域的版本常用于探索和解釋財富的分布，特別是不平等的趨勢。 在糖域的網格中，每個細胞都有一個容量，這是它可容納的最大糖量。 在原始狀態中，有兩個高糖區域，容量為 4，周圍是同心環，容量分別為 3, 2 和 1。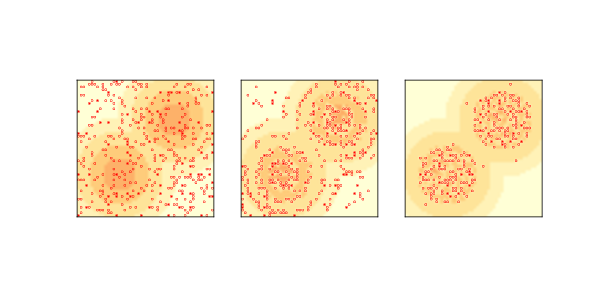  圖 9.3：原始糖域模型的復制品：初始狀態（左），2 步后（中）和 100 步后（右）。 圖？（左）展示了初始狀態，最黑暗的區域表示容量最高的細胞，小圓圈表示智能體。 最初有隨機放置的 400 個智能體。 每個智能體有三個隨機選擇的屬性： 糖： 每個智能體最開始都有先天的糖分，從 5 到 25 之間均勻選擇。 代謝： 在每個時間步驟中，每個智能體都必須消耗一定數量的糖，從 1 到 4 之間均勻選擇。 視力： 每個智能體可以“看到”附近細胞中糖量，并移動到最多的細胞，但是與其它智能體相比，一些智能體可以看到更遠的細胞。 智能體看到的距離從 1 和 6 之間均勻選擇。 在每個時間步驟中，智能體以隨機順序一次移動一格。 每個智能體都遵循以下規則： + 智能體在 4 個羅盤方向的每一個方向上調查`k`個細胞，其中`k`是智能體的視野范圍。 + 它選擇糖分最多的未占用的細胞。 在相等的情況下，選擇較近的細胞；在距離相同的細胞中，它隨機選擇。 + 智能體移動到選定的細胞并收獲糖分，將收獲增加到其積累的財富并將細胞清空。 + 智能體根據代謝消耗其財富的一部分。 如果結果總量為負數，智能體“餓死”并被刪除。 在所有智能體完成這些步驟之后，細胞恢復一些糖，通常為 1 單位，但每個細胞中的總糖分受其容量限制。 圖？（中）顯示兩步后模型的狀態。 大多數智能體正在移到糖最多的地區。 視力高的智能體移動速度最快；視力低的智能體往往會卡在高原上，隨機游走，直到它們足夠接近來看到下一個水平。 出生在糖分最少的地區的智能體可能會餓死，除非他們的視力很好，先天條件也很高。 在高糖地區，隨著糖分的出現，智能體相互競爭，尋找和收獲糖分。 消耗高或視力低的智能體最有可能挨餓。 當糖在每個時間步驟增加 1 個單位時，就沒有足夠的糖來維持我們開始的 400 個智能體。 人口起初迅速下降，然后緩慢下降，在大約 250 左右停下。 圖？（右）顯示了 100 個時間步后的模型狀態，大約有 250 個智能體。 存活的智能體往往是幸運者，出生時視力高和/或代消耗低。 存活到這里的話，它們可能會永遠存活，積累無限量的糖。 ## 9.5 財富的不平等 在目前的形式下，糖域建立了一個簡單的生態學模型，可用于探索模型參數之間的關系，如增長率和智能體的屬性，以及系統的承載能力（在穩定狀態下生存的智能體數量）。 它模擬了一種形式的自然選擇的，“適應度”較高的智能體更有可能生存下來。 該模型還表現出一種財富不平等，一些智能體積累糖的速度比其他智能體快。 但是對于財富分布，很難說具體的事情，因為它不是“靜止的”。 也就是說，分布隨著時間的推移而變化并且不會達到穩定狀態。 然而，如果我們給智能體有限的壽命，這個模型會產生固定的財富分布。 然后我們可以運行實驗，來查看參數和規則對此分布的影響。 在這個版本的模型中，智能體的年齡在每個時間步增加，并且從 60 到 100 之間的均勻分布中，隨機選擇一個壽命。如果智能體的年齡超過其壽命，它就會死亡。 當智能體因饑餓或年老而死亡時，它由屬性隨機的新智能體所取代，所以總人口是不變的。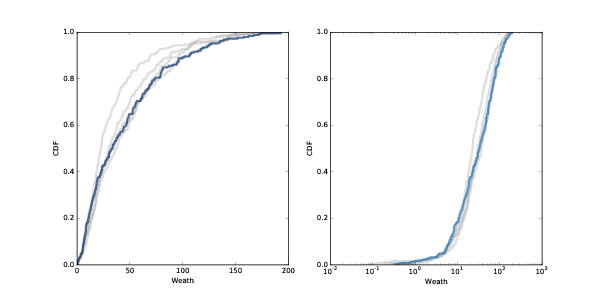  圖 9.4：100, 200, 300 和 400 步（灰線）和 500 步（黑線）之后的糖（財富）的分布。 線性刻度（左）和對數刻度（右）。 從接近承載能力的 250 個智能體開始，我運行了 500 個步驟的模型。 在每 100 步之后，我繪制了智能體積累的糖的分布。 圖？在線性刻度（左）和對數刻度（右）中展示結果。 經過大約 200 步（這是最長壽命的兩倍）后，分布變化不大。 并且它向右傾斜。 大多數智能體積累的財富很少：第 25 百分位數大約是 10，中位數大約是 20。但是少數智能體積累了更多：第 75 百分位數是大約 40，最大值大于 150。 在對數刻度上，分布的形狀類似于高斯或正態分布，但右尾被截斷。 如果它在對數刻度上實際上是正態的，則分布是對數正態分布，這是一種重尾分布。 實際上，幾乎每個國家和全世界的財富分布都是重尾分布。 如果說糖域解釋了為什么財富分布是重尾的，但是糖域變化中的不平等的普遍性表明，不平等是許多經濟體的特征，甚至是非常簡單的經濟體。 一些實驗表明避免或減輕并不容易，它們帶有一些規則，對納稅和其他收入轉移進行建模。 ## 9.6 實現糖域 糖域比以前的模型更復雜，所以我不會在這里介紹整個實現。 我將概述代碼的結構，你可以在 Jupyter 筆記本`chap09.ipynb`中查看本章的細節，它位于本書的倉庫中。 如果你對細節不感興趣，你可以跳到下一節。 以下是帶有`step`方法的`Agent`類： ```py class Agent: def step(self, env): self.loc = env.look_around(self.loc, self.vision) self.sugar += env.harvest(self.loc) - self.metabolism self.age += 1 ``` 在每個步驟中，智能體移動，收獲糖，并增加年齡。 參數`env`是環境的引用，它是一個`Sugarscape`對象。 它提供了方法`look_around`和收獲： + `look_around`獲取智能體的位置，這是一個坐標元組，以及智能體的視野，它是一個整數。 它返回智能體的新位置，這是糖分最多的可見細胞。 + `harvest `需要智能體的（新）位置，并在移除并返回該位置的糖分。 這里是`Sugarscape`類和它的`step`方法（不需要替換）： ```py class Sugarscape(Cell2D): def step(self): # loop through the agents in random order random_order = np.random.permutation(self.agents) for agent in random_order: # mark the current cell unoccupied self.occupied.remove(agent.loc) # execute one step agent.step(self) # if the agent is dead, remove from the list if agent.is_starving(): self.agents.remove(agent) else: # otherwise mark its cell occupied self.occupied.add(agent.loc) # grow back some sugar self.grow() return len(self.agents) ``` `Sugarscape`繼承自`Cell2D`，因此它與我們所見過的其他基于網格的模型相似。 這些屬性包括`agents`，它是`Agent`對象的列表，以及`occupied`，它是一組元組，其中每個元組包含智能體占用的細胞的坐標。 在每個步驟中，`Sugarscape`以隨機順序遍歷智能體。 它調用每個智能體的`step`，然后檢查它是否已經死亡。 所有智能體都移動后，一些糖會恢復。 如果你有興趣深入了解 NumPy ，你可能需要仔細看看`make_visible_locs`，它構建一個數組，其中每行包含智能體可見的細胞坐標，按距離排序，但距離相同的細胞 是隨機順序。 你可能想看看`Sugarscape.make_capacity`，它初始化細胞的容量。 它演示了`np.meshgrid`的使用，這通常很有用，但需要一些時間才能理解。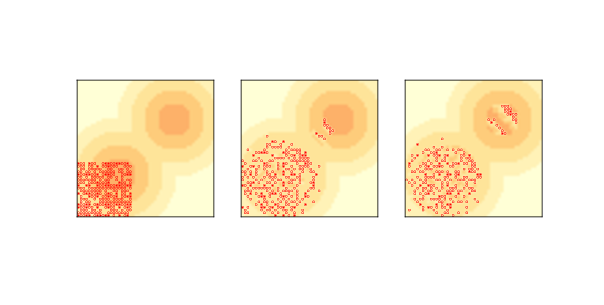 ## 9.7 遷移和波動行為  圖 9.5：`Sugarscape`中的波動行為：初始狀態（左），6 步后（中）和 12 步后（右） 雖然`Sugarscape`的主要目的不是探索空間中的智能體的移動，但 Epstein 和 Axtell 在智能體遷移時，觀察到一些有趣的模式。 如果我們開始把所有智能體放在左下角，他們會迅速走向最近的高容量細胞的“山峰”。 但是如果有更多的智能體，單個山峰不足以支持它們的話，他們很快就會耗盡糖分，智能體被迫進入低容量地區。 視野最長的那些，首先穿過山峰之間的山谷，并且像波一樣向東北方向傳播。 因為他們在身后留下一些空細胞，所以其他智能體不會追隨，直到糖分恢復。 結果是一系列離散的遷移波，每個波都像一個連貫的物體，就像我們在規則 110 CA 和生命游戲中看到的飛船（參見第？節）。 圖？顯示了初始條件下（左），6 個步驟（中）和 12 個步驟（右）之后的模型狀態。 你可以看到，前兩個波到達并穿過第二個山峰，留下了一串空細胞。 你還可以看到這個模型的動畫版本，其中波形更清晰可見。 雖然這些波動由智能體組成，但我們可以將他們視為自己的實體，就像我們在“生命游戲”中想到的滑翔機一樣。 這些波動的一個有趣的屬性是，它們沿對角線移動，這可能是令人驚訝的，因為這些智能體本身只是向北或向東移動，從不向東北方移動。 像這樣的結果 - 團隊或“集合”擁有智能體沒有的屬性和行為 - 在基于智能體的模型中很常見。 我們將在下一章看到更多的例子。 ## 9.8 涌現 本章中的例子展示了復雜性科學中最重要的想法之一：涌現。 涌現性是系統的一個特征，由它的成分相互作用而產生，而不是它們的屬性。 為了澄清什么是涌現，考慮它不是什么會有幫助。 例如，磚墻很硬，因為磚和砂漿很硬，所以這不是涌現。 再舉一個例子，一些剛性結構是由柔性部件構成的，所以這看起來像是一種涌現。 但它至多是一種弱例，因為結構特性遵循已知的力學定律。 相反，我們在謝林模型中看到的隔離是一種涌現，因為它不是由種族主義智能體造成的。 即使智能體只是輕微排外，系統的結果與智能體的決策意圖有很大不同。 糖域中的財富分配可能是涌現，但它是一個弱例，因為我們可以根據視力，代謝和壽命的分布合理預測它。 我們在最后一個例子中看到的波動行為可能是一個更強的例子，因為波動顯示出智能體顯然沒有的能力 - 對角線運動。 涌現性令人驚訝：即使我們知道所有規則，也很難預測系統的行為。難度不是偶然的；事實上，它可能是涌現的決定性特征。 正如沃爾夫勒姆在“新科學”中所討論的那樣，傳統科學是基于這樣的公理：如果你知道管理系統的規則，那么你可以預測它的行為。 我們所謂的“法律”通常是計算的捷徑，它使我們能夠預測系統的結果而不用建立或觀察它。 但是許多細胞自動機在計算上是不可減少的，這意味著沒有捷徑。 獲得結果的唯一方法是實現該系統。 一般而言，復雜系統可能也是如此。 對于具有多個成分的物理系統，通常沒有產生解析解的模型。 數值方法提供了一種計算捷徑，但仍存在質的差異。 解析解通常提供用于預測的恒定時間算法；也就是說，計算的運行時間不取決于預測的時間尺度`t`。 但數值方法，模擬，模擬計算和類似方法需要的時間與`t`成正比。 對于許多系統來說，我們無法計算出可靠的預測。 這些觀察表明，涌現性基本上是不可預測的，對于復雜系統我們不應該期望，通過計算捷徑來找到自然規律。 對某些人來說，“涌現”是無知的另一個名字; 根據這種思維，如果我們針對它沒有還原論的解釋，那么這個屬性就是涌現的，但如果我們在將來更好地理解它，它就不再是涌現的。 涌現性的狀況是有爭議的話題，所以對此持懷疑態度是恰當的。 當我們看到明顯的涌現性時，我們不應該假設永遠不會有還原論解釋。但我們也不應該假設必須有。 本書中的例子和計算等價原理提供了很好的理由，認為至少有些涌現性永遠不會被古典還原論模型“解釋”。 你可以在這里深入了解涌現：<http://en.wikipedia.org/wiki/Emergence>。 ## 9.9 練習 練習 1 本章的代碼位于本書倉庫的 Jupyter 筆記本`chap09.ipynb`中。打開這個筆記本，閱讀代碼，然后運行單元格。你可以使用這個筆記本來練習本章的練習。我的解決方案在`chap09soln.ipynb`中。 練習 2 《The Big Sort》的作者 Bill Bishop 認為，美國社會越來越由政見所隔離，因為人們選擇生活在志趣相投的鄰居之中。 Bishop 所假設的機制并不是像謝林模型中的智能體那樣，如果他們是孤立的，他們更有可能移動，但是當他們出于任何原因移動時，他們可能會選擇一個社區，其中的人與他們自己一樣。 修改謝林模型的實現來模擬這種行為，看看它是否會產生類似程度的隔離。 有幾種方法可以模擬 Bishop 的假設。在我的實現中，隨機選擇的智能體會在每個步驟中移動。每個智能體考慮`k`個隨機選擇的空位置，并選擇相似鄰居的比例最高的位置。隔離程度和`k`有什么關系？ 練習 3 在糖域的第一個版本中，我們從不添加智能體，所以一旦人口下降，它就不會恢復。 在第二個版本中，我們只是在智能體死亡時才取代，所以人口是不變的。 現在讓我們看看如果我們增加一些“人口壓力”會發生什么。 編寫糖域的一個版本，在每一步結束時添加一個新的智能體。 添加代碼來計算每個步驟結束時，智能體的平均視力和平均消耗。 運行模型幾百步，繪制人口，平均視力和平均消耗隨時間的變化。 你應該能夠通過繼承`SugarScape`并覆蓋`__init__`和`step`來實現這個模型。 練習 4 在心靈哲學中，強人工智能是這樣的理論，即受到適當編程的計算機可以擁有思想，與人類擁有的思想相同。 約翰·塞爾（John Searle）提出了一個名為“中文房間”的思想實驗，旨在表明強 AI 是虛假的。 你可以在 <http://en.wikipedia.org/wiki/Chinese_room> 上閱讀。 對中文房間的論述的系統回復是什么？ 你對涌現的認識如何影響你對系統回復的反應？