# 四、無標度網絡 > 原文：[Chapter 4 Scale-free networks](http://greenteapress.com/complexity2/html/thinkcomplexity2005.html) > 譯者：[飛龍](https://github.com/wizardforcel) > 協議：[CC BY-NC-SA 4.0](http://creativecommons.org/licenses/by-nc-sa/4.0/) > 自豪地采用[谷歌翻譯](https://translate.google.cn/) 在本章中，我們將處理來自在線社交網絡的數據，并使用 WS 圖對其進行建模。WS 模型像數據一樣，具有小世界網絡的特點，但是與數據不同，它的節點到節點的鄰居數目變化很小。 這種差異是 Barabási 和 Albert 開發的網絡模型的動機。BA 模型捕捉到鄰居數量的觀察到的變化，它具有小的世界屬性之一，短路徑長度，但它沒有一個小世界網絡的高聚類。 本章最后討論了 WS 和 BA 圖，作為小世界網絡的解釋模型。 本章的代碼位于本書的倉庫中的`chap04.ipynb`中。使用代碼的更多信息，請參見第（？）章。 ## 4.1 社交網絡數據 WS 圖的目的是，模擬自然科學和社會科學中的網絡。Watts 和 Strogatz 在他們最初的論文中，查看了電影演員的網絡（如果他們出現在同一部電影中，就是連接的）。美國西部的電網；和 C. elegans 線蟲腦中的神經元網絡 。他們發現，所有這些網絡都具有小世界圖的高群聚性和短路徑長度特征。 在本節中，我們將使用不同的數據集，Facebook 用戶及其朋友的數據集，來進行相同的分析。如果你對 Facebook 不熟悉，那么彼此連接的用戶被稱為“朋友”，而不管他們在現實世界中的關系的性質如何。 我將使用來自斯坦福網絡分析項目（SNAP）的數據，該項目分享了來自在線社交網絡和其他來源的大型數據集。具體來說，我將使用他們的 Facebook 數據集 [1]，其中包括 4039 個用戶和 88,234 個朋友關系。該數據集位于本書的倉庫中，但也可以從 [SNAP 網站](https://snap.stanford.edu/data/egonets-Facebook.html)上獲取。 > [1] J. McAuley and J. Leskovec. Learning to Discover Social Circles in Ego Networks. NIPS, 2012. 數據文件為每條邊包含一行，用戶由 0 到 4038 之間的整數標識。下面是讀取文件的代碼： ```py def read_graph(filename): G = nx.Graph() array = np.loadtxt(filename, dtype=int) G.add_edges_from(array) return G ``` NumPy 提供了函數`loadtext`，它讀取給定的文件，并以 NumPy 數組的形式返回內容。參數`dtype`指定數組元素的類型。 然后我們可以使用`add_edges_from`迭代數組的行，并創建邊。結果如下： ```py >>> fb = read_graph('facebook_combined.txt.gz') >>> n = len(fb) >>> m = len(fb.edges()) >>> n, m (4039, 88234) ``` 節點和邊的數量與數據集的文檔一致。 現在我們可以檢查這個數據集是否具有小世界圖的特征：高群聚性和短路徑長度。 第（？）節中，我們編寫了一個函數，來計算網絡平均群聚系數。NetworkX 提供了一個叫做的函數`average_clustering`，它可以更快地完成相同的工作。 但是對于更大的圖，它們都太慢，需要與`nk^2`成正比的時間，其中`n`是節點數，`k`是每個節點的鄰居數。 幸運的是，`NetworkX`提供了一個通過隨機抽樣來估計群聚系數的函數。你可以像這樣調用它： ```py from networkx.algorithms.approximation import average_clustering average_clustering(G, trials=1000) ``` 下面函數對路徑長度做了類似的事情： ```py def random_path_lengths(G, nodes=None, trials=1000): if nodes is None: nodes = G.nodes() else: nodes = list(nodes) pairs = np.random.choice(nodes, (trials, 2)) lengths = [nx.shortest_path_length(G, *pair) for pair in pairs] return lengths ``` `G`是一個圖，`nodes`是節點列表，我們應該從中抽樣，`trials`是要抽樣的隨機路徑的數量。如果`nodes`是`None`，我們從整個圖表中進行抽樣。 `pairs`是隨機選擇的節點的 NumPy 數組，對于每個采樣有一行兩列。 列表推導式枚舉數組中的行，并計算每對節點之間的最短距離。結果是路徑長度的列表。 `estimate_path_length`生成一個隨機路徑長度列表，并返回它們的平均值： ```py def estimate_path_length(G, nodes=None, trials=1000): return np.mean(random_path_lengths(G, nodes, trials)) ``` 我會使用`average_clustering `來計算`C`： ```py C = average_clustering(fb) ``` 并使用`estimate_path_lengths`來計算`L`： ```py L = estimate_path_lengths(fb) ``` 群聚系數約為`0.61`，這是較高的，正如我們所期望的那樣，如果這個網絡具有小世界特性。 平均路徑為`3.7`，在 4000 多個用戶的網絡中相當短。畢竟這是一個小世界。 現在讓我們看看是否可以構建一個 WS 圖，與此網絡具有相同特征。 ## 4.2 WS 模型 在 Facebook 數據集中，每個節點的平均邊數約為 22。由于每條邊都連接到兩個節點，度的均值是每個節點邊數的兩倍： ```py >>> k = int(round(2*m/n)) >>> k 44 ``` 我們可以用`n=4039`和`k=44`創建一個 WS 圖。`p=0`時，我們會得到一個環格。 ```py lattice = nx.watts_strogatz_graph(n, k, 0) ``` 在這個圖中，群聚較高：`C`是 0.73，而在數據集中是 0.61。但是`L`為 46，遠遠高于數據集！ 使用`p=1`我們得到一個隨機圖： ```py random_graph = nx.watts_strogatz_graph(n, k, 1) ``` 在隨機圖中，`L`是 2.6，甚至比數據集（3.7）短，但`C`只有 0.011，所以這是不好的。 通過反復試驗，我們發現，當`p=0.05`時，我們得到一個高群聚和短路徑長度的 WS 圖： ```py ws = nx.watts_strogatz_graph(n, k, 0.05, seed=15) ``` 在這個圖中`C`是`0.63`，比數據集高一點，`L`是 3.2，比數據集低一點。所以這個圖很好地模擬了數據集的小世界特征。 到現在為止還不錯。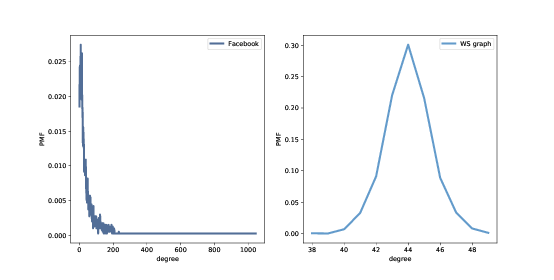 ## 4.3 度  > 圖 4.1：Facebook 數據集和 WS 模型中的度的 PMF。 回想一下，節點的度是它連接到的鄰居的數量。如果 WS 圖是 Facebook 網絡的一個很好的模型，它應該具有相同的總（或平均）度，理想情況下不同節點的度數相同。 這個函數返回圖中的度的列表，每個節點對應一項： ```py def degrees(G): return [G.degree(u) for u in G] ``` 數據集中的度的均值是 43.7；WS 模型中的度的均值是 44。到目前為止還不錯。 但是，WS 模型中的度的標準差為 1.5；數據中的標準差是 52.4。有點糟。 這里發生了什么？為了更好地查看，我們必須看看度的 分布，而不僅僅是均值和標準差。 我將用一個 Pmf 對象來表示度的分布，它在`thinkstats2`模塊中定義。Pmf 代表“概率質量函數”；如果你不熟悉這個概念，你可以閱讀 Think Stats 第二版的第三章，網址是 <http://greenteapress.com/thinkstats2/html/thinkstats2004.html>。 簡而言之，Pmf 是值到概率的映射。Pmf 是每個可能的度`d`，到度為`d`的節點比例的映射。 作為一個例子，我將構建一個圖，擁有節點`1, 2, 3`，連接到中心節點`0`： ```py G = nx.Graph() G.add_edge(1, 0) G.add_edge(2, 0) G.add_edge(3, 0) nx.draw(G) ``` 這里是圖中的度的列表： ```py >>> degrees(G) [3, 1, 1, 1] ``` 節點`0`度為 3，其它度為 1。現在我可以生成一個 Pmf，它表示這個度的分布： ```py >>> from thinkstats2 import Pmf >>> Pmf(degrees(G)) Pmf({1: 0.75, 3: 0.25}) ``` 產生的`Pmf`是一個對象，將每個度映射到一個比例或概率。在這個例子中，75％的節點度為 1，25％度為 3。 現在我們生成一個`Pmf`，包含來自數據集的節點的度，并計算均值和標準差： ```py >>> pmf_ws = Pmf(degrees(ws)) >>> pmf_ws.mean(), pmf_ws.std() (44.000, 1.465) ``` 我們可以使用`thinkplot`模塊來繪制結果： ```py thinkplot.Pdf(pmf_fb, label='Facebook') thinkplot.Pdf(pmf_ws, label='WS graph') ``` 圖（？）顯示了這兩個分布。他們是非常不同的。 在 WS 模型中，大多數用戶有大約 44 個朋友；最小值是 38，最大值是 50。這個變化不大。在數據集中，有很多用戶只有 1 或 2 個朋友，但有一個人有 1000 多個！ 像這樣的分布，有許多小的值和一些非常大的值，被稱為重尾。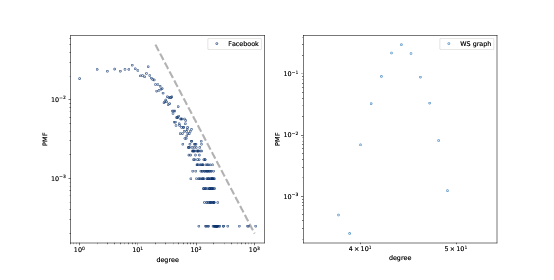 ## 4.4 重尾分布  > 圖 4.2：Facebook 數據集和 WS 模型中的度的 PMF，在雙對數刻度下。 在復雜性科學的許多領域中，重尾分布是一個常見特征，它們將成為本書的一個反復出現的主題。 我們可以在雙對數軸繪制它，來獲得重尾分布的更清晰的圖像，就像上面那副圖那樣。這種轉換突顯了分布的尾巴；也就是較大值的概率。 在這種轉換下，數據大致在一條直線上，這表明分布的最大值與概率之間存在“冪律”關系。在數學上， ``` PMF(k) ~ k^(?α) ``` 其中`PMF(k)`是度為`k`的節點的比例，`α`是一個參數，符號`~`表示當`k`增加時，PMF 漸近于`k^(?α)`。 如果我們把對兩邊取對數，我們得到： ``` logPMF(k) ~ ?α logk ``` 因此，如果一個分布遵循冪律，并且我們在雙對數刻度上繪制`PMF(k)`與`k`的關系，那么我們預計至少對于`k`的較大值，將有一條斜率為`-α`的直線。 所有的冪律分布都是重尾的，但是還有其他重尾分布不符合冪律。我們將很快看到更多的例子。 但首先，我們有一個問題：WS 模型擁有高群聚性和短路徑長度，我們在數據中也看到了，但度的分布根本不像數據。這種差異就啟發了我們下一個主題，Barabási-Albert 模型。 ## 4.5 Barabási-Albert 模型 1999 年，Barabási 和 Albert 發表了一篇論文“隨機網絡中的標度的出現”（Emergence of Scaling in Random Networks），描述了幾個現實世界的網絡的結構特征，包含一些圖，它們展示了電影演員，萬維網（WWW）頁面和美國西部電網設施的互聯性。你可以從 <http://www.sciencemag.org/content/286/5439/509> 下載該論文。 他們測量每個節點的度并計算`PMF(k)`，即節點度為`k`的比例。然后他們在雙對數標度上繪制`PMF(k)`與`k`的關系。這些曲線可用一條直線擬合，至少對于`k`的較大數值；所以他們得出結論，這些分布是重尾的。 他們還提出了一個模型，生成了屬性相同的圖。模型的基本特征與 WS 模型不同，它們是： 增長： BA 模型不是從固定數量的頂點開始，而是從一個較小圖開始，每次添加一個頂點。 優先連接： 當創建一個新的邊時，它更可能連接到一個已經有很多邊的節點。這種“富者更富”的效應是一些現實世界網絡增長模式的特征。 最后，他們表明，由 Barabási-Albert（BA）模型模型生成的圖，度的分布遵循冪律。 具有這個屬性的圖有時被稱為無標度網絡，原因我不會解釋；如果你好奇，可以在 <http://en.wikipedia.org/wiki/Scale-free_network> 上閱讀更多內容。 NetworkX 提供了一個生成 BA 圖的函數。我們將首先使用它；然后我會告訴你它的工作原理。 ```py ba = nx.barabasi_albert_graph(n=4039, k=22) ``` 參數是`n`要生成的節點數量，`k`是每個節點添加到圖形時的起始邊數。我選擇`k=22`，是因為這是數據集中每個節點的平均邊數。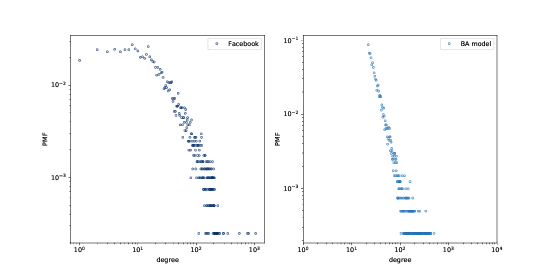  > 圖 4.3：Facebook 數據集和 BA 模型中的節點的 PMF，在雙對數刻度上。 所得圖形擁有 4039 個節點，每個節點有 21.9 個邊。由于每條邊連接兩個節點，度的均值為 43.8，非常接近數據集中的度的均值 43.7。 度的標準差為 40.9，略低于數據集 52.4，但比我們從 WS 圖得到的數值好 1.5 倍。 圖（？）以雙對數刻度展示了 Facebook 網絡和 BA 模型的度的分布。模型并不完美；特別`k`是在小于 10 時偏離了數據。但尾巴看起來像是一條直線，這表明這個過程產生了遵循冪律的度的分布。 所以在重現度的分布時，BA 模型比 WS 模型更好。但它有小世界的屬性？ 在這個例子中，平均路徑長度`L`是 2.5，這比實際的網絡的`L = 3.69`更小。所以這很好，雖然可能太好了。 另一方面，群聚系數`C`為 0.037，并不接近數據集中的值 0.61。所以這是一個問題。 下表總結了這些結果。WS 模型捕獲了小世界的特點，但沒有度的分布。BA 模型捕獲了度的分布，和平均路徑長度，至少是近似的，但沒有群聚系數。 在本章最后的練習中，你可以探索其他可以捕獲所有這些特征的模型。 | | Facebook | WS 模型 | BA 模型 | | --- | --- | --- | --- | | `C` | 0.61 | 0.63 | 0.037 | | `L` | 3.69 | 3.23 | 2.51 | | 度的均值 | 43.7 | 44 | 43.7 | | 度的標準差 | 52.4 | 1.5 | 40.1 | | 冪律？ | 可能 | 不是 | 是 | > 表 4.1：與兩個模型相比，Facebook 網絡的特征。 ## 4.6 生成 BA 圖 在前面的章節中，我們使用了 NetworkX 函數來生成BA圖。現在讓我們看看它的工作原理。這是一個`barabasi_albert_graph`的版本，我做了一些更改，使其更易于閱讀： ```py def barabasi_albert_graph(n, k): G = nx.empty_graph(k) targets = list(range(k)) repeated_nodes = [] for source in range(k, n): G.add_edges_from(zip([source]*k, targets)) repeated_nodes.extend(targets) repeated_nodes.extend([source] * k) targets = _random_subset(repeated_nodes, k) return G ``` `n`是我們想要的節點的數量，`k`是每個新節點邊的數量（近似為每個節點的邊的數量）。 我們從一個`k`個節點和沒有邊的圖開始。然后我們初始化兩個變量： `targets`： `k`個節點的列表，它們將被連接到下一個節點。最初`targets`包含原來的`k`個節點；之后它將包含節點的隨機子集。 `repeated_nodes`： 一個現有節點的列表，如果一個節點有`k`條邊，那么它出現`k`次。當我們從`repeated_nodes`選擇時，選擇任何節點的概率與它所具有的邊數成正比。 每次循環中，我們添加源節點到`targets`中的節點的邊。然后我們更新`repeated_nodes`，通過添加每個目標一次，以及新的節點`k`次。 最后，我們選擇節點的子集作為下一次迭代的目標。以下是`_random_subset`的定義： ```py def _random_subset(repeated_nodes, k): targets = set() while len(targets) < k: x = random.choice(repeated_nodes) targets.add(x) return targets ``` 每次循環中，`_random_subset`從`repeated_nodes`選擇，并將所選節點添加到`targets`。因為`targets`是一個集合，它會自動丟棄重復項，所以只有當我們選擇了`k`不同的節點時，循環才會退出。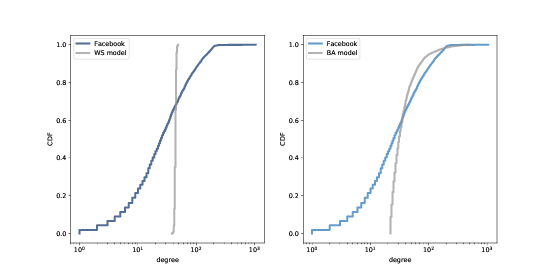 ## 4.7 累積分布函數（CDF）  > 圖 4.4：Facebook 數據集中的度的 CDF，以及 WS 模型（左邊）和 BA 模型（右邊），在雙對數刻度上。 圖 4.3 通過在雙對數刻度上繪制概率質量函數（PMF）來表示度的分布。這就是 Barabási 和 Albert 呈現他們的結果的方式，這是冪律分布的文章中最常使用的表示。但是，這不是觀察這樣的數據的最好方法。 更好的選擇是累積分布函數 （CDF），它將`x`值映射為小于或等于`x`的值的比例。 給定一個 Pmf，計算累積概率的最簡單方法是將`x`的概率加起來，包括`x`： ```py def cumulative_prob(pmf, x): ps = [pmf[value] for value in pmf if value<=x] return sum(ps) ``` 例如，給定數據集中的度的分布，`pmf_pf`，我們可以計算好友數小于等于 25 的比例： ```py >>> cumulative_prob(pmf_fb, 25) 0.506 ``` 結果接近 0.5，這意味著好友數的中位數約為 25。 因為 CDF 的噪音比 PMF 少，所以 CDF 更適合可視化。一旦你習慣了 CDF 的解釋，它們可以提供比 PMF 更清晰的分布圖像。 `thinkstats`模塊提供了一個稱為`Cdf`的類，代表累積分布函數。我們可以用它來計算數據集中的度的 CDF。 ```py from thinkstats2 import Cdf cdf_fb = Cdf(degrees(fb), label='Facebook') ``` `thinkplot`提供了一個函數，叫做`Cdf`，繪制累積分布函數。 ```py thinkplot.Cdf(cdf_fb) ``` 圖 4.4 顯示了 Facebook 數據集的度的 CDF ，以及 WS 模型（左邊）和 BA 模型（右邊）。`x`軸是對數刻度。 顯然，WS 模型和數據集的 CDF 很大不同。BA 模式更好，但還不是很好，特別是對于較小數值。 在分布的尾部（值大于 100），BA 模型看起來與數據集匹配得很好，但是很難看出來。我們可以使用另一個數據視圖，更清楚地觀察數據：在對數坐標上繪制互補 CDF。 互補 CDF（CCDF）定義為： ``` CCDF(x) = 1 ? CDF(x) ``` 它很有用，因為如果 PMF 服從冪律，CCDF 也服從： ``` CCDF(x) =(x/x_m)^(-α) ``` 其中`x_m`是最小可能值，`α`是確定分布形狀的參數。 對兩邊取對數： ``` logCCDF(x) = ?α (logx ? logx_m) ``` 因此，如果分布服從冪定律，在雙對數刻度上，我們預計 CCDF 是斜率為`-α`的直線。 圖 4.5 以雙對數刻度顯示 Facebook 數據的度的 CCDF，以及 WS 模型（左邊）和 BA 模型（右邊）。 通過這種查看數據的方式，我們可以看到 BA 模型與分布的尾部（值大于 20）匹配得相當好。WS 模型沒有。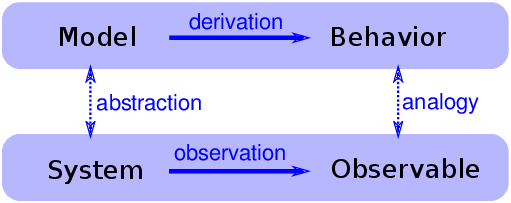 ## 4.8 解釋性模型  > 圖 4.6：解釋性模型的邏輯結構 我們以 Milgram 的小世界實驗開始討論網絡，這表明社交網絡中的路徑長度是驚人的小；因此，有了“六度分離”。 當我們看到令人驚訝的事情時，自然會問“為什么”，但有時候我們不清楚我們正在尋找什么樣的答案。一種答案是解釋性模型（見圖 4.6）。解釋性模型的邏輯結構是： 1. 在一個系統`S`中，我們看到一些可觀察的東西`O`，值得解釋。 2. 我們構建一個與系統類似的模型`M`，也就是說，模型與系統之間的元素/組件/原理是對應的。 3. 通過模擬或數學推導，我們表明，該模型展現出類似于`O`的行為`B`。 4. 我們得出這樣的結論：`S`表現`O`，因為 `S`類似于`M`，`M`表示`B`，而`B`類似于`O`。 其核心是類比論證，即如果兩個事物在某些方面相似，那么它們在其他方面可能是相似的。 類比論證是有用的，解釋模型可以令人滿意，但是它們并不構成數學意義上的證明。 請記住，所有的模型都有所忽略，或者“抽象掉”我們認為不重要的細節。對于任何系統都有很多可能的模型，它們包括或忽略不同的特性。而且可能會出現不同的行為模式，`B`，`B'`和`B''`，這些模式與`O`不同。在這種情況下，哪個模型解釋了`O`？ 小世界現象就是一個例子：Watts-Strogatz（WS）模型和 Barabási-Albert（BA）模型都展現出小世界行為的元素，但是它們提供了不同的解釋： + WS 模型表明，社交網絡是“小”的，因為它們包括強連通的集群，和連接群集的“弱關系”（參見 <http://en.wikipedia.org/wiki/Mark_Granovetter#The_strength_of_weak_ties>）。 + BA 模型表明，社交網絡很小，因為它們包括度較高的節點，作為中心，并且隨著時間的推移，由于優先添加，中心??會增長。 在科學的新興領域，往往是這樣，問題不是我們沒有解釋，而是它們太多。 ## 4.9：練習 練習 1： 上一節中，我們討論了小世界現象的兩種解釋，“弱關系”和“中心”。這些解釋是否兼容？也就是說，他們能都對嗎？你覺得哪一個解釋更令人滿意？為什么？ 是否有可以收集的數據或可以執行的實驗，它們可以提供有利于一種模型的證據？ 競爭模型中的選擇，是托馬斯·庫恩（Thomas Kuhn）的論文“客觀性，價值判斷和理論選擇”（Objectivity, Value Judgment, and Theory Choice）的主題，你可以在 <https://github.com/AllenDowney/ThinkComplexity2/blob/master/papers/kuhn.pdf> 上閱讀。 對于競爭模型中的選擇，庫恩提出了什么標準？這些標準是否會影響你對 WS 和 BA 模型的看法？你認為還有其他標準應該考慮嗎？ 練習 2： NetworkX 提供了一個叫做`powerlaw_cluster_graph`的函數，實現了 Holme 和 Kim 算法，用于使用度的冪律分布和近似平均聚類，使圖增長。閱讀該函數的文檔，看看是否可以使用它來生成一個圖，節點數、度的均值和群聚系數與 Facebook 數據集相同。與實際分布相比較，模型中的度的分布如何？ 練習 3： 來自 Barabási 和 Albert 論文的數據文件可從 <http://www3.nd.edu/~networks/resources.htm> 獲得。他們的演員協作數據包含在名為`actor.dat.gz`的文件中。以下函數讀取文件并構建圖。 ```py import gzip def read_actor_network(filename, n=None): G = nx.Graph() with gzip.open(filename) as f: for i, line in enumerate(f): nodes = [int(x) for x in line.split()] G.add_edges_from(thinkcomplexity.all_pairs(nodes)) if n and i >= n: break return G ``` 計算圖中的演員數量和度的均值。以雙對數刻度繪制度的 PMF。同時在對數-線性刻度上繪制度的 CDF，來觀察分布的一般形狀，并在雙對數刻度上觀察，尾部是否服從冪律。 注意：演員的網絡不是連通的，因此你可能想要使用`nx.connected_component_subgraphs`查找節點的連通子集。