# 六、生命游戲 > 原文：[Chapter 6 Game of Life](http://greenteapress.com/complexity2/html/thinkcomplexity2007.html) > 譯者：[飛龍](https://github.com/wizardforcel) > 協議：[CC BY-NC-SA 4.0](http://creativecommons.org/licenses/by-nc-sa/4.0/) > 自豪地采用[谷歌翻譯](https://translate.google.cn/) 在本章中，我們考慮二維細胞自動機，特別是 John Conway 的生命游戲（GoL）。 像上一章中的一些 CA 一樣，GoL 遵循簡單的規則并產生令人驚訝的復雜行為。 就像沃爾夫勒姆的規則 110 一樣，事實證明 GoL 是通用的；也就是說，至少在理論上它可以計算任何可計算的函數。 GoL 的復雜行為引發了科學哲學問題，特別是科學現實主義和工具主義的相關問題。 我討論這些問題并提出擴展閱讀的建議。 在本章的最后，我演示了如何在 Python 中高效實現 GoL。 本章的代碼位于本書倉庫的`chap06.ipynb`中。 使用代碼的更多信息，請參見第？節。 ## 6.1 Conway 的生命游戲 首先要研究的細胞自動機之一，也許是有史以來最受歡迎的一種，是稱為“生命游戲”的二維 CA，簡稱 GoL。 它由 John H. Conway 開發并于 1970 年在《科學美國人》（Scientific American）的馬丁加德納（Martin Gardner）專欄中推廣。 請參閱 <http://en.wikipedia.org/wiki/Conway_Game_of_Life>。 GoL 中的細胞排列在一個二維網格中，兩個方向上都有限，或者首尾相接。 雙向首尾相接的網格稱為環面，因為它在地形上等同于多納圈的表面。 見 <http://en.wikipedia.org/wiki/Torus>。 每個細胞有兩個狀態 - 生存和死亡 - 和八個鄰居 - 東西南北和四個對角線。 這些鄰居有時被稱為“摩爾鄰域”。 就像前面章節中的一維 CA 一樣，生命游戲按照規則演變，這就像物理學的簡單定律。 在 GoL 中，每個單元格的下一個狀態取決于其當前狀態和活動鄰居的數量。 如果一個細胞是活的，如果它有兩個或三個活動鄰居就會生存，否則就會死亡。 如果一個細胞是死的，它將保持死亡，除非它恰好有三個鄰居。 下表總結了這些規則： | 當前狀態 | 鄰居數量 | 下一個狀態 | | --- | --- | --- | | 生存 | 2–3 | 生存 | | 生存 | 0–1, 4–8 | 死亡 | | 死亡 | 3 | 生存 | | 死亡 | 0–2, 4–8 | 死亡 | 這種行為與真正的細胞生長大致類似：分離或過度擁擠的細胞死亡；它們在中等密度下蓬勃成長。 GoL 很受歡迎，因為： 有簡單的初始條件產生令人驚訝的復雜行為。 有許多有趣的穩定圖案：有些擺動（以不同的周期），有些像 Wolfram 的 CA 規則 110 中的飛船一樣移動。 和規則 110 一樣，GoL 是圖靈完整的。 另一個產生興趣的因素是康威的猜測 - 沒有可以使活細胞數量無限增長的初始條件 - 以及他向任何可以證明或否定它的人提供的 50 美元賞金。 最后，計算機日益增加的可用性，使得自動化計算并以圖形方式顯示結果成為可能。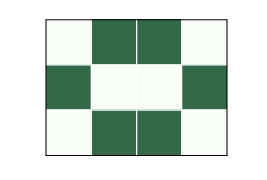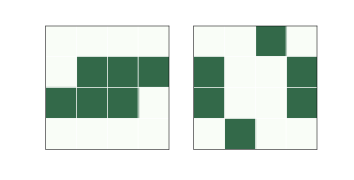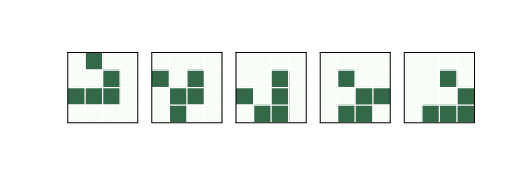 ## 6.2 生命圖案  圖 6.1：一個靜態圖案，叫做“蜂巢”（beehive）  圖 6.2：一個振蕩圖案，叫做“蟾蜍”（toad）  圖 6.3：一個飛船，叫做“滑翔機”（glider） 如果從隨機起始狀態運行 GoL，可能會出現一些穩定圖案。隨著時間的推移，人們已經確定了這些圖案并給了它們名字 例如，圖？展示了一種稱為“蜂巢”的穩定圖案。蜂巢中的每個細胞都有兩個或三個鄰居，所以它們都能存活下來，蜂巢旁邊的死細胞都沒有三個鄰居，所以沒有新細胞誕生。 其他圖案在“振蕩”；也就是說，它們隨著時間而改變，但最終返回到它們的起始狀態（只要它們不與另一個圖案沖突）。例如，圖？展示了一種稱為“蟾蜍”的圖案，它是在兩種狀態之間交替的振蕩圖案。這個振蕩圖案的“周期”是二。 最后，一些圖案振蕩并返回到起始狀態，但在空間中移動。因為這些圖案似乎在移動，所以它們被稱為“飛船”。 圖？展示了一艘名為“滑翔機”的飛船。經過四段時間后，滑翔機回到起始位置，并向下和向右移動一個單位。 根據起始方向，滑翔機可以沿著四條對角線中的任何一條移動。還有其它的水平和垂直移動的飛船。 人們花費了大量時間來查找和命名這些圖案。如果你搜索網頁，你會發現很多收藏品。 ## 6.3 Conwey 的推測 從最初的條件來看，GoL 迅速達到穩定狀態，活細胞數量幾乎不變（可能帶有一些振蕩）。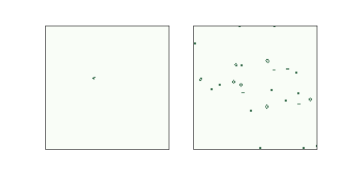  圖 6.4：r-pentomino 的開始和最終狀態 但是一些簡單的開始條件，需要很長時間才能穩定下來，并產生令人驚訝的活細胞數量。 這些模式被稱為“Methuselahs”，因為它們很長壽。 其中最簡單的是 r-pentomino，它只有五個細胞，形狀大致為字母“r”。 圖？顯示了 r-pentomino 的初始狀態和 1103 步后的最終狀態。 這種狀態是“最終的”，因為所有剩余圖案是穩定的，振蕩的或滑翔機，它們永遠不會與另一種圖案相沖突。 r-pentomino 總共產生 6 個滑翔機，8 個積木（block），4 個閃光燈（blinker），4 個蜂巢，1 個小艇（boat），1 個輪船（ship）和 1 個面包（loaf）。  圖 6.5：Gosper 的滑翔機槍，產生滑翔機流。 長壽圖案的存在，使得康威懷疑是否存在從未穩定的初始圖案。 他猜想沒有，但他描述了兩種證明他是錯誤的圖案，“槍”（gun）和“蒸汽火車”（puffer train）。 槍是穩定的模式，定期產生飛船 - 隨著飛船流從源位置移動，活細胞的數量無限增長。 蒸汽火車是一種將活細胞留在尾部的平移圖案。 事實證明，這兩種模式都存在。 由 Bill Gosper 領導的一個小組發現了第一個，它是現在稱為 Gosper's Gun 的滑翔槍，如圖所示。 Gosper 還發現了第一個蒸汽火車。 這兩種類型都有很多圖案，但它們很難設計或找到。 這不是巧合。 Conway 選擇了 GoL 的規則，這樣他的猜想就不會明顯為真或假。 在二維 CA 的所有可能規則中，大多數產生簡單的行為：大多數初始條件快速穩定或無限增長。 通過避免無趣的 CA，Conway 也避免了 Wolfram 的一類和二類行為，并且可能還有三類。 如果我們相信 Wolfram 的計算等價原則，我們預計 GoL 會屬于第四類，而且是這樣。 生命游戲在 1982 年被證明了圖靈的完整性（1983年也是獨立的）。 從那時起，幾個人構建了 GoL 模式，實現了圖靈機或另一臺已知圖靈完備的機器。 ## 6.4 現實主義 GoL中的穩定模式很難不被注意，特別是那些移動的模式。 將它們視為持久的實體是很自然的事，但請記住，CA 是由細胞構成的；沒有蟾蜍或面包這樣的東西。 滑翔機和其他飛船甚至更不真實，因為隨著時間的推移，它們甚至不由相同的細胞組成。 所以這些圖案就像星座一樣。 我們這樣看待他們，因為我們善于觀察圖案，或者因為我們有活躍的想象力，但他們不是真實的。 對嘛？ 好吧，不是那樣。 我們認為“真實”的許多實體，也是規模較小的實體的持久圖案。 颶風只是氣流的模式，但我們給了他們個人名稱。 而人就像滑翔機，隨著時間的推移不是由相同細胞組成的。 但即使你更換了你體內的每一個細胞，我們也認為你是同一個人。 這不是一個新觀察 - 大約在 2500 年前，赫拉克利特（Heraclitus）指出你不能在同一條河流中兩次 - 但是出現在生命游戲中的實體，是思考哲學現實主義的實用測試用例。 在哲學的背景下，現實主義是這樣一種觀點，即世界中的實體存在與人類的感知和概念無關。 “感知”是指我們從感官中獲得的信息，而“概念”是指我們形成的世界的心智模式。 例如，我們的視覺系統將一些東西感知為場景的二維投影，我們的大腦使用該圖像構建場景中物體的三維模型。 科學實在論與科學理論和他們所假設的實體有關。 如果一個理論使用實體的屬性和行為來表達，那么這個理論假設了一個實體。 例如，電磁學的理論用電場和磁場表示。 經濟學的一些理論以供給，需求和市場力量來表達。 生物學的理論是用基因來表達的。 但這些實體是真實的嗎？ 也就是說，它們存在于獨立于我們和我們的理論的世界嗎？ 再次，我發現，在一系列強度中陳述哲學立場是有用的；這里有四個科學現實主義的陳述，強度逐漸增加： SR1： 對于它們接近現實的程度，科學理論為真或假，但沒有理論是完全正確的。 一些所假設的實體可能是真實的，但沒有原則性的方式來說出哪些是真實的。 SR2： 隨著科學的進步，我們的理論會變得更加逼近現實。 至少有一些所假定的實體是已知真實的。 SR3： 有些理論是完全正確的；其他近似真實。 真實理論所假設的實體，以及近似真實理論中的一些實體是真實的。 SR4： 如果一個理論正確地描述了現實，那么這個理論就是真的，否則就是假。真實理論所假設的實體是真實的；其他不是。 SR4 非常強，可能是站不住腳的；通過這樣一個嚴格的標準，幾乎所有當前的理論都被認為是錯誤的。 大多數現實主義者會接受 SR1 和 SR3 之間的東西。 ## 6.5 工具主義 但 SR1 很弱以至于它接近工具主義，這是一種觀點，我們不能說理論是真是假，因為我們不知道理論是否符合現實。 理論是我們用于我們的目的的工具；在適用于其目的的程度上，理論是有用的，或者不是。 要看看你是否對工具主義感到滿意，請考慮以下陳述： “生命游戲中的實體并不是真實的；他們只是人們賦予可愛的名字的細胞圖案。” “颶風只是一種氣流模式，但它是一種有用的描述，因為它可以讓我們進行有關天氣的預測和溝通。” “像本我和超我這樣的弗洛伊德實體并不是真實的，但它們是思考和交流心理學的有用工具（或者至少有些人是這么認為的）。” “電磁場是我們最好的電磁理論中的假設實體，但它們并不真實。 我們可以構建其他理論，而不用場的假設，這也是一樣有用的。” “我們認為，世界上的許多物體都是像星座一樣的任意集合。 例如，蘑菇只是真菌的子實體，其中大部分是在地下生長的，幾乎不連續的細胞網絡。 我們由于實際原因專注于蘑菇，如可見性和可愛。” “有些物體邊界清晰，但很多都是模糊的。 例如，哪些分子是你身體的一部分：你的肺里的空氣？ 你的胃里的食物？ 你血液中的營養物質？ 細胞中的營養物質？ 細胞中的水？ 細胞的結構部分？ 頭發？ 死皮？ 污垢？ 你的皮膚上的細菌？ 你的腸道細菌？線粒體？ 當你稱量自己時，你包含了多少這些分子？ 根據離散對象構想世界是有用的，但我們確定的實體并不是真實的。” 對于每一個你同意的陳述，給自己一分。 如果你的分數超過 4 分，你可能會成為一名工具主義者！ 如果你比其他人更喜歡這些陳述，那么問問你自己為什么。 這些情景中的哪些差異會影響你的反應？ 你能否在他們之間做出原則性區分？ 工具主義的更多信息，請參閱 <http://en.wikipedia.org/wiki/Instrumentalism>。 ## 6.6 實現 本章最后的練習要求你嘗試和修改生命游戲，并實現其他二維細胞自動機。 本節介紹 GoL 的實現，你可以將其用作實驗的起始位置。 為了表示細胞的狀態，我使用類型為`uint8`的 NumPy 數組，它是一個 8 位無符號整數。 例如，下面這行創建一個 10 乘 10 的數組，并用 0 和 1 的隨機值進行初始化。 ```py a = np.random.randint(2, size=(10, 10)).astype(np.uint8) ``` 我們可以用幾種方法計算 GoL 規則。 最簡單的方法是使用`for`循環遍歷數組的行和列： ```py b = np.zeros_like(a) rows, cols = a.shape for i in range(1, rows-1): for j in range(1, cols-1): state = a[i, j] neighbors = a[i-1:i+2, j-1:j+2] k = np.sum(neighbors) - state if state: if k==2 or k==3: b[i, j] = 1 else: if k == 3: b[i, j] = 1 ``` 最初，`b`是一個與`a`大小相同的零數組。 每次循環中，狀態是中心細胞的條件，鄰居是`3×3`的鄰域。 `k`是活動鄰居的數量（不包括中心細胞）。 嵌套的`if`語句評估 GoL 規則并相應地激活`b`中的細胞。 這個實現是規則的直接翻譯，但它是冗長而緩慢的。 我們可以使用互相關做得更好，正如我們在第？節中看到的那樣。 在那里，我們使用`np.correlate`來計算一維相關。 現在，為了計算二維相關，我們將使用`scipy.signal`中的`correlate2d`，它是一個 SciPy 模塊，提供信號處理的相關函數： ```py from scipy.signal import correlate2d kernel = np.array([[1, 1, 1], [1, 0, 1], [1, 1, 1]]) c = correlate2d(a, kernel, mode='same') ``` 在一維相關的背景下，我們稱之為“窗口”的內容，在二維相關的背景下被稱為“核”，但其想法是相同的：`correlate2d`將核和數組相乘來選擇一個鄰域，然后將結果加起來。 這會核選擇中心細胞周圍的 8 個鄰居。 `correlate2d`將核應用于數組中的每個位置。 使用`mode ='same'`時，結果與`a`的大小相同。 現在我們可以使用邏輯運算符來計算規則： ```py b = (c==3) | (c==2) & a b = b.astype(np.uint8) ``` 第一行計算了一個布爾數組，其中應該有活細胞的地方為`True`，其他地方為`False`。 然后，`astype`將布爾數組轉換為整數數組。 這個版本更快，也許夠好，但是我們可以通過修改核來簡化它： ```py kernel = np.array([[1, 1, 1], [1,10, 1], [1, 1, 1]]) c = correlate2d(a, kernel, mode='same') b = (c==3) | (c==12) | (c==13) b = b.astype(np.uint8) ``` 這個版本核的包含中心單元并賦予其權重 10。如果中心單元為 0，則結果介于 0 和 8 之間; 如果中心單元為 1，則結果在 10 到 18 之間。使用這個核，我們可以簡化邏輯運算，只選擇值為 3，12 和 13 的細胞。 這看起來可能不是什么大的改進，但它允許進一步簡化：使用這個核，我們可以使用一個表來查找細胞的值，就像我們在第？節中所做的那樣。 ```py table = np.zeros(20, dtype=np.uint8) table[[3, 12, 13]] = 1 c = correlate2d(a, kernel, mode='same') b = table[c] ``` 除了位置 3，12 和 13 以外，表格中的任何位置都為零。當我們使用`c`作為表格中的索引時，NumPy 執行逐元素查找；也就是說，它從`c`中獲取每個值，在表中查找它并將結果放入`b`中。 這個版本比其他版本更快更簡潔， 唯一的缺點是需要更多的解釋。 包含在本書倉庫中的`Life.py`提供了一個封裝規則實現的`Life`類。 如果你執行`Life.py`，你應該看到一個“蒸汽火車”的動畫，這是一種飛船，在其尾部留下一串碎屑。 ## 6.7 練習 練習 1 本章的代碼位于本書倉庫的 Jupyter 筆記本`chap06.ipynb`中。 打開這個筆記本，閱讀代碼，然后運行單元格。 你可以使用這個筆記本來練習本章的練習。 我的解決方案在`chap06soln.ipynb`中。 練習 2 以隨機狀態啟動 GoL 并運行它直至穩定。 你可以識別哪些穩定的圖案？ 練習 3 許多命名圖案都以便攜式文件格式提供。 修改`Life.py`來解析其中一種格式并初始化網格。 練習 4 一種最長壽的小型圖案是“兔子”，它以 9 個活動細胞開始，需要 17 331 個步驟來穩定。 你可以在 <http://www.conwaylife.com/wiki/Rabbits> 獲取各種格式的初始狀態。 加載此狀態并運行它。 練習 5 在我的實現中，`Life`類基于一個名為`Cell2D`的父類，`LifeViewer`基于`Cell2DViewer`。 你可以使用這些基類來實現其他二維細胞自動機。 例如，GoL 的一個變體叫做“Highlife”，與 GoL 規則相同，另外還有一條規則：有 6 個鄰居的死亡細胞會變活。 編寫一個名為`Highlife`的類，該類繼承自`Cell2D`并實現這個版本的規則。 另外編寫一個名為`HighlifeViewer`的類，該類繼承自`Cell2DViewer`并嘗試以不同的方式來展示結果。 作為一個簡單的例子，使用不同的顏色表。 `Highlife`中更有趣的圖案之一是復制器（replicator）。 使用`add_cells`和復制器初始化`Highlife`并查看它做了什么。 練習 6 如果將圖靈機擴展到兩個維度，或者將讀寫頭添加到二維 CA，則結果是稱為 Turmite 的細胞自動機。由于讀寫頭移動的方式，它以白蟻（termite）命名，但拼寫錯誤是對 Alan Turing 的敬意。 最著名的 Turmite 是 1986 年由 Chris Langton 發現的蘭頓的螞蟻（Langton's Ant）。請見 <http://en.wikipedia.org/wiki/Langton_ant>。 螞蟻（ant）是一個具有四種狀態的讀寫頭，你可以將其視為面向東、西、南或北。細胞有兩種狀態，黑色和白色。 規則很簡單。在每個時間步驟中，螞蟻檢查它所在單元格的顏色。如果是黑色，螞蟻轉向右轉，將細胞變成白色，并向前移動一個格子。如果細胞是白色的，螞蟻會向左轉，將細胞變成黑色，然后向前移動。 給定一個簡單的世界，一組簡單的規則，并且只有一個可移動的部分，你可能會期望看到簡單的行為 - 但你現在應該更清楚。從所有的白色細胞開始，在進入周期為 104 步的循環之前，蘭頓的螞蟻以看似隨機的方式移動超過 10000 步。每個循環后，螞蟻都會沿對角線平移，因此會留下一條稱為“高速路”的蹤跡。 編寫蘭頓的螞蟻的實現。