[TOC] ## 1\. 數組[?](https://blog.yorek.xyz/leetcode/code_interviews_1/#1 "Permanent link") ### 1.1 (3)數組中重復的數字[?](https://blog.yorek.xyz/leetcode/code_interviews_1/#11-3 "Permanent link") #### 1.1.1 找出數組中重復的數字[?](https://blog.yorek.xyz/leetcode/code_interviews_1/#111 "Permanent link") > 在一個長度為n的數組里的所有數字都在0到n-1的范圍內。數組中某些數字是重復的，但不知道有幾個數字重復了，也不知道每個數字重復了幾次。請找出數組中任意一個重復的數字。例如，如果輸入長度為7的數組{2, 3, 1, 0, 2, 5, 3}，那么對應的輸出是重復的數字2或者3。 **解法一：先排序，后遍歷** 排序后找到重復的數字是非常容易的事情，只需要從頭到尾掃描排序后的數組就可以了。 排序一個長度為n的數組需要O(nlogn)的時間 **解法二：哈希表** 從頭到尾掃描，每掃到一個數字，可以用O(1)的時間判斷哈希表中是否已經包含了該數字。如果沒有包含，就把它加入哈希表。否則，就找到了重復數字。 其時間復雜度為O(n)，空間復雜度也為O(n) **解法三：利用數組的特點** 我們注意到數組中的數字都在0~n-1的范圍內。如果數組中沒有重復元素，那么數組排序后數字i將會出現在下標為i的位置。如果有重復的元素，那么有些位置可能存在多個數字，同時有些位置可能沒有數字。 我們從頭到尾遍歷數組。當掃描到下標為i的數字時，首先比較這個數字(m)是不是i。如果是，則接著掃描下一個數字；如果不是，拿它和第m個數字進行比較。如果它和第m個數字相等，就找到了一個重復的數字(該數字在下標i和m的位置都出現了)。如果它和第m個數字不相等，就把第i個數字和第m個數字交換，把m放到屬于它的位置。接下來再重復這個比較、交換的過程。 ~~~ private int duplicate(int[] numbers, int length) { if (numbers == null || length == 0) { return -1; } for (int i = 0; i < length; i++) { if (numbers[i] < 0 || numbers[i] >= length) { return -1; } } for (int i = 0; i < length; i++) { while (numbers[i] != i) { if (numbers[i] == numbers[numbers[i]]) { return numbers[i]; } // swap int t = numbers[i]; numbers[i] = numbers[t]; numbers[t] = t; } } return -1; } ~~~ 此題思想和[LC—41—First Missing Positive](https://blog.yorek.xyz/leetcode/leetcode41-50/#41-first-missing-positive)思想類似。 #### 1.1.2 不修改數組找出重復的數字[?](https://blog.yorek.xyz/leetcode/code_interviews_1/#112 "Permanent link") > 在一個長度為n+1的數組里的所有數字都在1到n的范圍內，所以數組中至少有一個數字是重復的。請找出數組中任意一個重復的數字，但不能修改輸入的數組。例如，如果輸入長度為8的數組{2, 3, 5, 4, 3, 2, 6, 7}，那么對應的輸出是重復的數字2或者3。 **解法一：復制數組時排序** 我們可以創建一個長度為n+1的輔助數組，然后逐一輔助原數組中的每個數字。在復制時，如果原數組中被復制的數字是m，則把它復制到輔助數組中下標為m的位置。這樣就容易發現哪個數字是重復的。 該方法時間復雜度為O(1)，空間復雜度為O(n)。 **解法二：利用題設** > 在一個長度為n+1的數組里的所有數字都在1到n的范圍內，所以數組中至少有一個數字是重復的。 由于所有的數字都在1~n的范圍內，所以我們可以利用二分查找，在查找時統計一下某個區間里數字的數目。 我們把1~n的數字從中間的數字m分為兩部分，前面一半為1~m，后面一半為m+1~n。如果1~m的數字出現的次數超過m，那么這一半的區間里一定包含重復的數字；否則另一半區間里一定包含重復的數字。我們可以繼續把包含重復數字的區間一分為二，直到找到一個重復的數字。 該方法由于二分查找的特點，`countRange`方法會被調用O(logn)次，每次需要O(n)的時間，因此總時間復雜度是O(nlogn)，空間復雜度為O(1)。 ~~~ // 題設：n+1的數組里的所有數字都在1到n的范圍內 // 可以換成好理解的：n的數組里的所有數字都在1到n-1的范圍內 private int duplicate(int[] numbers, int length) { if (numbers == null || length == 0) { return -1; } for (int i = 0; i < length; i++) { if (numbers[i] < 0 || numbers[i] >= length) { return -1; } } // start、end是需要統計的數字的上下限 int start = 1; int end = length - 1; int mid = 0; while (end >= start) { mid = ((end - start) >> 1) + start; int count = countRange(numbers, start, mid); if (start == end) { if (count > 1) { // 找到了，當前指向的值就是重復數字 return start; } else { // 否則，沒有重復數字 break; } } // 如果區間內的出現的數字個數大于區間的長度，說明這個區間出現了重復數字 if (count > (mid - start + 1)) { // 此時重復的值可能就是mid，所以end=mid end = mid; } else { // 如果該區間沒有重復數字，那么mid肯定也不是，所以跳過mid start = mid + 1; } } return -1; } private int countRange(int[] numbers, int start, int end) { int count = 0; for (int i = 0; i < numbers.length; i++) { if (numbers[i] >= start && numbers[i] <= end) { count++; } } return count; } ~~~ ### 1.2 (4)二維數組中的查找[?](https://blog.yorek.xyz/leetcode/code_interviews_1/#12-4 "Permanent link") > 在一個二維數組中，每一行都按照從左到右遞增的順序排序，每一列都按照從上到下遞增的順序排序。請完成一個函數，輸入這樣的一個二維數組和一個整數，判斷數組中是否含有該整數。 下面就是一個示例數組。在其中查找7返回true，查找5返回false。 ~~~ 1 2 8 9 2 4 9 12 4 7 10 13 6 8 11 15 ~~~ 此題同[LC-74-Search a 2D Matrix](https://blog.yorek.xyz/leetcode/leetcode71-80/#74-search-a-2d-matrix) 我們利用每行每列都是遞增的規律，可以整行、整列地縮減查找范圍。 首選選取數組右上角的數字。如果數字等于要查找的數字，則查找過程結束；如果該數字大于要查找的數字，說明要查找的數字位于該列左邊，所以剔除這個數字所在的列；如果該數字小于要查找的數字，說明要查找的數字位于改行下方，所以剔除這個數字所在的行。這樣每一步都可以縮小查找的方位，直到找到數字或查找結束。 ~~~ boolean find(int[][] matrix, int rows, int columns, int number) { if (matrix == null || rows == 0 || columns == 0) { return false; } int row = 0; int col = columns - 1; while (row < rows && col >= 0) { if (matrix[row][col] == number) { return true; } else if (matrix[row][col] > number) { col--; } else { row++; } } return false; } ~~~ 在上面的代碼中，我們選取的右上角的數字。同樣，我們也可以選擇左下角的數字，也可以逐步減小查找范圍。其他兩個角因為是最小值、最大值，無法逐步減小查找范圍。 ~~~ int row = rows - 1; int col = 0; while (col < columns && row >= 0) { if (matrix[row][col] == number) { return true; } else if (matrix[row][col] > number) { row--; } else { col++; } } ~~~ ## 2\. 字符串[?](https://blog.yorek.xyz/leetcode/code_interviews_1/#2 "Permanent link") ### 2.1 (5)替換空格[?](https://blog.yorek.xyz/leetcode/code_interviews_1/#21-5 "Permanent link") > 請實現一個函數，把字符串中的每個空格替換成"%20"。例如輸入“We are happy.”，則輸出“We%20are%20happy.”。 **解法一：順序查找空格，找到后插入%20** 假設字符串的長度為n。對于每個空格字符，需要移動和面O(n)個字符，對于含有O(n)個空格字符的字符串而言，總的時間效率是O(n^2)。 **解法二：計算空格個數，從后往前替換空格** 我們可以先遍歷一次字符串，統計出空格的總數，由此可以計算出新串的總長度。然后從字符串的后面（或前面）開始復制和替換，方向沒有多少區別。 ~~~ String replaceBlank(String str) { if (str == null || "".equals(str)) { return str; } // 統計空格的個數 int spaceCount = 0; for (int i = 0; i < str.length(); i++) { if (str.charAt(i) == ' ') { spaceCount++; } } // 如果不包含空格，就可以直接返回原來的字符串 if (spaceCount == 0) { return str; } // 申請新串，準備復制 final int newStrLength = str.length() + spaceCount * 2; char[] result = new char[newStrLength]; int index = newStrLength - 1; // 在原來的串上從后往前遍歷 for (int i = str.length() - 1; i >= 0; i--) { if (str.charAt(i) == ' ') { // 遇到一個空格，則在新串上填上%20 result[index--] = '0'; result[index--] = '2'; result[index--] = '%'; } else { // 復制原來的字符 result[index--] = str.charAt(i); } } return new String(result); } ~~~ 也可以在Java中直接使用`StringBuilder`的特點解決此問題： ~~~ String replaceBlank(String str) { if (str == null || "".equals(str)) { return str; } StringBuilder result = new StringBuilder(); for (int i = 0; i < str.length(); i++) { char ch = str.charAt(i); if (ch == ' ') { result.append("%20"); } else { result.append(ch); } } return result.toString(); } ~~~ 相關題目 有兩個排序的數組A1和A2，內存在A1的末尾有足夠多的剩余空間容納A2。請實現一個函數，把A2中的所有數字插入A1中，并且所有的數字是排序的。 和前面的例題一樣，很多人首先想到的辦法是在A1中從頭到尾復制數字，但這樣就會出現多次復制一個數字的情況。更好的的方法是**從尾到頭**比較A1和A2中的數字，并把較大的數字復制到A1中的合適位置。 舉一反三 在合并兩個數組時，如果從前往后復制每個數字需要重復移動數字多次，那么我們可以考慮從后往前復制，這樣就能減少移動的次數，從而提高效率。 ## 3\. 鏈表[?](https://blog.yorek.xyz/leetcode/code_interviews_1/#3 "Permanent link") ### 3.1 (6)從尾到頭打印鏈表[?](https://blog.yorek.xyz/leetcode/code_interviews_1/#31-6 "Permanent link") > 輸入一個鏈表的頭結點，從尾到頭反過來打印出每個結點的值。 通常打印只是一個只讀操作，我們不希望打印時修改內容。 此題如果想把鏈表中鏈接節點的指針反轉過來，改變鏈表的方向，這樣就太蠢了，而且也會改變原來鏈表的結構。 我們可以想到遍歷時使用`Stack`保存節點的值，然后全部出棧就可以了。 **解法一：利用棧** ~~~ private void printListReversingly1(ListNode pHead) { ListNode p = pHead; Stack<Integer> stack = new Stack<>(); while (p != null) { stack.push(p.value); p = p.next; } while (!stack.isEmpty()) { System.out.print(stack.pop() + "\t"); } } ~~~ 既然想到了用棧實現，而遞歸本質上就是一個棧結構，所以我們也可以利用遞歸實現。 要反過來輸出鏈表，我們每訪問一個節點時，先遞歸輸出它后面的節點，再輸出該節點自身，這樣就實現了目的。 **解法二：遞歸** ~~~ private void printListReversingly2(ListNode pHead) { if (pHead != null) { printListReversingly1(pHead.next); System.out.print(pHead.value + "\t"); } } ~~~ 上面的代碼看起來很簡潔，但**當鏈表非常長的時候，就會導致函數調用的層級很深，從而導致函數調用棧溢出**。顯然用棧基于循環實現的代碼魯棒性要好一點。 ## 4\. 樹[?](https://blog.yorek.xyz/leetcode/code_interviews_1/#4 "Permanent link") 樹的邏輯結構很簡單：除根節點之外的每個節點只有一個父節點，根節點沒有父節點；除葉節點之外所有節點都有一個或多個子節點，葉節點沒有子節點。父節點與子節點之間用指針鏈接。 我們常提到的樹是二叉樹，通常二叉樹有如下幾種遍歷方式。 * **前序遍歷**：根左右，即先訪問根節點，再訪問左子節點，最后訪問右子節點。 圖中二叉樹的前序遍歷的順序是，10、6、4、8、14、12、16 * **中序遍歷**：左根右，即先訪問左子節點，再訪問根節點，最后訪問右子節點。 圖中二叉樹的中序遍歷的順序是，4、6、8、10、12、14、16 * **后序遍歷**：左右根，即先訪問左子節點，再訪問右子節點，最后訪問根節點。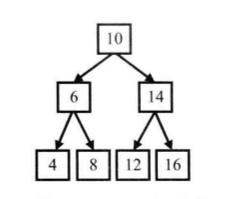 圖中二叉樹的中序遍歷的順序是，4、8、6、12、16、14、10  這三種遍歷方式都有遞歸和循環2種實現方式，每種遍歷的遞歸實現都比循環實現要簡潔很多。我們應該對這3中遍歷的6種實現方法都了如指掌。 * **寬度優先遍歷**：先訪問樹的第一層節點，再訪問樹的第二層節點……一直到訪問到最下面一層節點。在同一層節點中，以從左到右的順序依次訪問。我們可以對包括二叉樹在內的所有樹進行寬度優先遍歷。 圖中二叉樹的寬度優先遍歷的順序是：10、6、14、4、8、12、16 ### 樹的遍歷算法[?](https://blog.yorek.xyz/leetcode/code_interviews_1/#_1 "Permanent link") ~~~ /** * 前序遍歷遞歸算法 */ private static void preorderRecursive(BinaryTreeNode node) { if (node != null) { System.out.print(" " + node.value); preorderRecursive(node.left); preorderRecursive(node.right); } } /** * 前序遍歷循環算法 * 從根節點開始，每訪問一節點時，先訪問左子樹，同時若右子樹存在，則將右子樹進棧 */ private static void preorderIterative(BinaryTreeNode node) { if (node == null) { return; } Stack<BinaryTreeNode> stack = new Stack<>(); BinaryTreeNode p; // 根節點進棧 stack.push(node); while (!stack.isEmpty()) { // 開始訪問當前棧頂的元素 p = stack.pop(); while (p != null) { // 訪問當前棧頂的元素 System.out.print(" " + p.value); // 若右節點存在，則將右子樹進棧 if (p.right != null) { stack.push(p.right); } // 繼續沿著左子樹訪問 p = p.left; } } } /** * 中序遍歷遞歸算法 */ private static void inorderRecursive(BinaryTreeNode node) { if (node != null) { inorderRecursive(node.left); System.out.print(" " + node.value); inorderRecursive(node.right); } } /** * 中序遍歷循環算法 * 從根節點開始，沿著左子樹找到該子樹在中序下的第一節點(同時保存每個節點到棧內)，訪問該節點 * 然后訪問該節點的右子樹 */ private static void inorderIterative(BinaryTreeNode node) { if (node == null) { return; } Stack<BinaryTreeNode> stack = new Stack<>(); BinaryTreeNode p; // 根節點進棧 stack.push(node); while (!stack.isEmpty()) { // 開始訪問棧頂的元素 p = stack.peek(); // 若左子樹存在，一直將左子樹壓進棧 while (p != null) { stack.push(p.left); p = stack.peek(); } // 彈出棧頂的空元素 stack.pop(); if (!stack.isEmpty()) { // 葉節點或沒有左子樹的節點 p = stack.pop(); // 訪問當前棧頂的元素 System.out.print(" " + p.value); // 將右子樹進棧，在循環的開始就能處理右子樹了 stack.push(p.right); } } } /** * 后序遍歷遞歸算法 */ private static void postorderRecursive(BinaryTreeNode node) { if (node != null) { postorderRecursive(node.left); postorderRecursive(node.right); System.out.print(" " + node.value); } } private static class NodeWrapper { public BinaryTreeNode node; /** * false表示左子樹壓入的 * true表示右子樹壓入的 */ public boolean tag; } /** * 后序遍歷循環算法 * 對于一個節點是否能夠訪問，要看它的左右子樹是否遍歷完 * 首先從根節點開始，沿著左子樹開始遍歷，將途中所有節點全部標記并壓入棧中 * 然后取棧頂元素，如果能夠訪問右子樹，則沿著右子樹開始遍歷，將途中所有節點全部標記并壓入棧中 * 若左右都訪問完畢，則訪問自身這個節點 */ private static void postorderIterative(BinaryTreeNode node) { if (node == null) { return; } Stack<NodeWrapper> stack = new Stack<>(); BinaryTreeNode p = node; NodeWrapper wrapper; while (p != null || !stack.isEmpty()) { // 沿著左子樹開始遍歷，將途中所有節點全部標記并壓入棧中 while (p != null) { wrapper = new NodeWrapper(); wrapper.node = p; wrapper.tag = false; stack.push(wrapper); p = p.left; } // 取棧頂元素 wrapper = stack.pop(); p = wrapper.node; boolean find = wrapper.tag; if (!find) { // 能夠訪問右子樹，則沿著右子樹開始遍歷，將途中所有節點全部標記并壓入棧中 wrapper = new NodeWrapper(); wrapper.node = p; wrapper.tag = true; stack.push(wrapper); p = p.right; } else { // 左右都訪問完畢，則訪問自身這個節點 System.out.print(" " + p.value); p = null; } } } /** * 層序遍歷算法 */ private static void levelIterative(BinaryTreeNode node) { Queue<BinaryTreeNode> queue = new LinkedList<>(); queue.offer(node); while (!queue.isEmpty()) { node = queue.poll(); System.out.print(" " + node.value); if (node.left != null) { queue.offer(node.left); } if (node.right != null) { queue.offer(node.right); } } } ~~~ ### 樹的其他概念[?](https://blog.yorek.xyz/leetcode/code_interviews_1/#_2 "Permanent link") 若設二叉樹的深度為h，除第h層外，其它各層 (1～h-1) 的結點數都達到最大個數，第h層所有的結點都連續集中在最左邊，這就是**完全二叉樹**。 **二叉搜索樹、二叉查找樹、二叉排序樹**是一個概念：左子節點總是小于或者等于根節點，而右子節點總是大于或者等于根節點。 **平衡二叉樹AVL**是一顆二叉搜索樹，每個節點的左右子樹的高度差的絕對值（平衡因子）最多為1。 二叉樹有很多特例，**二叉搜索樹**就是其中之一。 在二叉搜索樹中，左子節點總是小于或者等于根節點，而右子節點總是大于或者等于根節點。上面練習樹的遍歷算法的二叉樹就是一顆二叉搜索樹。我們平均在O(logn)的時間內根據數值在二叉搜索樹中找到一個節點。 二叉樹的另外兩個特例是**堆**和**紅黑樹**。 * 堆分為**最大堆**和**最小堆**。在最大堆中根節點的值最大，在最小堆中根節點的值最小。有很多需要快速找到最大值或者最小值的問題都可以用堆解決。 最小堆、最大堆在Java中可以這樣實現： ~~~ // 最小堆 PriorityQueue<Integer> minHeap = new PriorityQueue<Integer>(); // 最大堆 PriorityQueue<Integer> maxHeap = new PriorityQueue<Integer>(n, new Comparator<Integer>(){ @Override public int compare(Integer o1, Integer o2) { return o2 - o1; } }); ~~~ * 關于紅黑樹，維基百科說的非常好：[紅黑樹](https://zh.wikipedia.org/wiki/%E7%BA%A2%E9%BB%91%E6%A0%91) **紅黑樹**是一種近似平衡的二叉查找樹，它把樹中的節點定義為紅、黑兩種顏色，并通過規則確保從根節點到葉節點的最長路徑的長度不超過最短路徑的兩倍。 具體來說，紅黑樹是滿足如下條件的二叉查找樹： 1. 每個節點要么是紅色，要么是黑色。 2. 根節點必須是黑色 3. 每個葉節點（在紅黑樹中指樹尾端的null節點）都是黑色 4. 紅色節點不能連續（也即是，紅色節點的孩子和父親都不能是紅色）。 5. 對于每個節點，從該點至null（樹尾端）的任何路徑，都含有相同個數的黑色節點。 一個紅黑樹例子如下：  這些約束確保了紅黑樹的關鍵特性：**從根到葉子的最長的可能路徑不多于最短的可能路徑的兩倍長。結果是這個樹大致上是平衡的**。 因為操作比如插入、刪除和查找某個值的最壞情況時間都要求與樹的高度成比例，這個在高度上的理論上限允許紅黑樹在最壞情況下都是高效的，而不同于普通的二叉查找樹。 要知道為什么這些性質確保了這個結果，注意到性質4導致了路徑不能有兩個毗連的紅色節點就足夠了。最短的可能路徑都是黑色節點，最長的可能路徑有交替的紅色和黑色節點。因為根據性質5所有最長的路徑都有相同數目的黑色節點，這就表明了沒有路徑能多于任何其他路徑的兩倍長。 在樹的結構發生改變時（插入或者刪除操作），往往會破壞上述條件4或條件5，需要通過調整使得查找樹重新滿足紅黑樹的條件。 調整可以分為兩類：一類是顏色調整，即改變某個節點的顏色；另一類是結構調整，集改變檢索樹的結構關系。結構調整過程包含兩個基本操作：左旋（Rotate Left），右旋（Rotate Right）。 Java中`TreeMap`底層通過紅黑樹來實現，這樣插入刪除都只有O(logn)的時間復雜度。 ### 4.1 (7)重建二叉樹[?](https://blog.yorek.xyz/leetcode/code_interviews_1/#41-7 "Permanent link") > 輸入某二叉樹的前序遍歷和中序遍歷的結果，請重建出該二叉樹。假設輸入的前序遍歷和中序遍歷的結果中都不含重復的數字。 > 例如輸入前序遍歷序列{1,2, 4, 7, 3, 5, 6, 8}和中序遍歷序列{4, 7, 2, 1, 5, 3, 8, 6}，則重建下圖所示的二叉樹并輸出它的頭結點。 此題同[LC-105-Construct Binary Tree from Preorder and Inorder Traversal](https://blog.yorek.xyz/leetcode/leetcode101-110/#105-construct-binary-tree-from-preorder-and-inorder-traversal) Tip 前序+中序、后序+中序、層序+中序都可以重建二叉樹，但是前序+后序不行。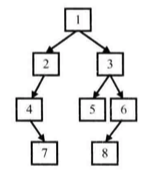  一個二叉樹例子 算法思路是先根據前序序列找到根節點，然后在中序序列中找到該節點，其左邊的就是樹的左子樹，右邊就是右子樹。 ~~~ private BinaryTreeNode construct(int[] preorder, int[] inorder, int length) throws Exception{ if (preorder == null || inorder == null || length <= 0) { return null; } return constructCore(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1); } private BinaryTreeNode constructCore( int[] preorder, int startPreorder, int endPreorder, int[] inorder, int startInorder, int endInorder ) throws Exception { // 如果發生了這種情況，說明前中序子序列為空，那么肯定就是空節點了 if (startInorder > endInorder || startPreorder > endPreorder) { return null; } // startPreorder即為根節點 BinaryTreeNode root = new BinaryTreeNode(preorder[startPreorder]); boolean find = false; int i = startInorder; for (; i <= endInorder; i++) { if (inorder[i] == root.value) { find = true; // 由于在中序序列中i是根節點，所以i-startInorder的長度就是左子樹的長度 // 因此重建左子樹時，左子樹的前序序列范圍就是startPreorder+1至startPreorder+1 + i-startInorder - 1 = startPreorder + i - startInorder // 左子樹的中序序列范圍就是startInorder至i - 1，沒有什么好說的 // 重建右子樹時類似 root.left = constructCore( preorder, startPreorder + 1, startPreorder + i - startInorder, inorder, startInorder, i - 1); root.right = constructCore( preorder, startPreorder + i - startInorder + 1, endPreorder, inorder, i + 1, endInorder); } } // 最后，如果根節點在中序序列中沒有找到，那么肯定是無效的輸入了 if (!find) { throw new Exception("invalid input"); } return root; } ~~~ ### 4.2 (8)二叉樹的下一個節點[?](https://blog.yorek.xyz/leetcode/code_interviews_1/#42-8 "Permanent link") > 給定一棵二叉樹和其中的一個結點，如何找出中序遍歷順序的下一個結點？樹中的結點除了有兩個分別指向左右子結點的指針以外，還有一個指向父結點的指針。 下圖中二叉樹的中序遍歷序列是{d, b, h, e, i, a, f, c, g}。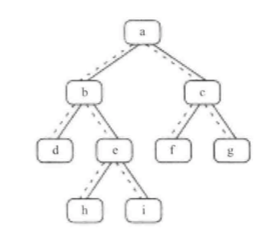  一顆有9個節點的二叉樹 我們以上面這顆樹為例分析如何找出二叉樹的下一個節點。 * *根*，如果一個節點有右子樹：那么它的下一個節點就是它的右子樹中的最左子節點。也就是說，從右子節點出發一直沿著指向左子節點的指針，我們就能找到它的下一個節點。 * *左*，如果一個節點沒有右子樹，同時節點是它父節點的左子節點，那么它的父節點就是要找的下一個節點。 * *右*，如果一個節點沒有右子樹，同時節點是它父節點的右子節點：我們需要沿著父節點一直向上，直到找到一個是它父節點的左子節點的節點。這個父節點就是我們要找的下一個節點。 ~~~ private ParentBinaryTreeNode getNext(ParentBinaryTreeNode node){ if (node == null) { return null; } ParentBinaryTreeNode next = null; if (node.right != null) { // 情況1 從右子節點出發一直沿著指向左子節點的指針 next = node.right; while (next.left != null) { next = next.left; } return next; } else if (node.parent != null) { // 情況2、3可以理解為同一種 2是3的一般情況 next = node; // 沿著父節點一直向上，直到找到一個節點，它是父節點的左子節點 // 即如果這個節點是父節點的右節點，那么繼續尋找 while (next.parent != null && next == next.parent.right) { next = next.parent; } // 最后這個父節點就是我們要找的下一個節點 return next.parent; } return next; } ~~~ ## 5\. 棧和隊列[?](https://blog.yorek.xyz/leetcode/code_interviews_1/#5 "Permanent link") 棧的特點是后進先出，通常棧是一個不考慮排序的數據結構，我們需要O(n)時間才能找到棧中最大或者最小的元素。如果想要在O(1)時間內得到棧的最大值或最小值，則需要對棧做特殊的設計，詳見(30)題“包含min函數的棧”。 隊列的特點是先進先出。 棧和隊列雖然是特點針鋒相對的兩個數據結構，但有意思的是他們卻相互聯系。 棧的常用操作為： * `isEmpty` * `peek` * `pop` * `push` 隊列的常用操作為： * `isEmpty` * `peek` * `poll` * `offer` ### 5.1 (9)用兩個棧實現隊列[?](https://blog.yorek.xyz/leetcode/code_interviews_1/#51-9 "Permanent link") > 用兩個棧實現一個隊列。隊列的聲明如下，請實現它的兩個函數appendTail和deleteHead，分別完成在隊列尾部插入結點和在隊列頭部刪除結點的功能。 ~~~ class JQueue<T> { private Stack<T> stack1 = new Stack<>(); private Stack<T> stack2 = new Stack<>(); public void appendTail(T element) { stack1.push(element); } public T deleteHead() { if (stack2.isEmpty()) { while (!stack1.isEmpty()) { stack2.push(stack1.pop()); } } if (stack2.isEmpty()) { return null; } return stack2.pop(); } } ~~~ 插入元素的時候直接插入stack1即可。 在刪除隊列的頭部的時候，如果stack2為空，那么把stack1的`pop`依次`push`進stack2。這樣操作后stack2中最上面就是最先進隊列的，也就是我們要求的。 相關題目 用兩個隊列實現一個棧。 ~~~ /** * 相關題目 * 用兩個隊列實現一個棧。 */ class JStack<T> extends Stack<T>{ private Queue<T> queue1 = new LinkedList<>(); private Queue<T> queue2 = new LinkedList<>(); @Override public T push(T item) { queue1.offer(item); return item; } @Override public synchronized T pop() { if (queue1.isEmpty()) { throw new EmptyStackException(); } while (queue1.size() > 1) { queue2.offer(queue1.poll()); } T item = queue1.poll(); Queue<T> tmp = queue1; queue1 = queue2; queue2 = tmp; return item; } public static void main(String[] args) { Stack<Integer> stack = new JStack<>(); stack.push(1); System.out.println(stack.pop()); stack.push(2); stack.push(3); System.out.println(stack.pop()); stack.push(4); System.out.println(stack.pop()); System.out.println(stack.pop()); // 輸出 1 3 4 2 } } ~~~ ## 6\. 算法和數據操作[?](https://blog.yorek.xyz/leetcode/code_interviews_1/#6 "Permanent link") 很多算法都可以用遞歸和循環兩種不同的方式實現。通常基于遞歸的實現方式代碼會比較簡潔，但性能不如基于循環的實現方式。 通常排序和查找時算法的重點。我們應該重點掌握二分查找、歸并排序和快速排序，能做到隨時正確、完整地寫出這些代碼。 如果要求在二維數組上搜索路徑，那么我們可以嘗試用回溯法。通常回溯法很適合用遞歸的代碼實現。只有限定不能用遞歸實現的時候，我們再考慮用棧來模擬遞歸的過程。 如果要求的是某個問題的最優解，而且該問題可以分為多個子問題，那么我們可以嘗試用動態規劃。在用自上而下的遞歸思路去分析動態規劃問題的時候，我們就會發現子問題之間存在重疊的更小的子問題。為了避免不必要的重復計算，我們用自下而上的循環代碼來實現，也就是把子問題的最優解先計算出來并用數組保存下來，接下來基于子問題的解計算大問題的解。 如果在分解子問題的時候存在某個特殊的選擇，如果采用這個特殊的選擇將一定得到最優解，那么這意味著可能適用于貪婪算法。 位運算可以看成一類特殊的算法，它是把數字表示成二進制之后對0和1的操作。它只有與、或、異或、左移、右移5種位運算。 ### 6.1 遞歸和循環[?](https://blog.yorek.xyz/leetcode/code_interviews_1/#61 "Permanent link") 如果我們需要重復地多次計算相同的問題，則通常可以選擇用遞歸或者循環兩種不同的方法。通常遞歸的代碼會比較簡潔。 雖然遞歸很簡潔，但它同時也有顯著的缺點。遞歸是函數調用自身，而函數調用時有時間和空間的消耗的，所以遞歸實現的效率不如循環。 另外，遞歸中有可能很多計算都是重復的，從而對性能帶來很大的負面影響。例如第10題“斐波那契數列”和第60題“n個骰子的點數”中，我們會分析遞歸和循環的性能區別。 通常應用動態規劃解決問題時我們都是用遞歸的思路分析問題，但由于遞歸分解的子問題中存在大量的重復，因此我們總是采用自下而上的循環來實現代碼。例如第14題“剪繩子”、第47題”禮物的最大價值”和第48題”最長不含重復數字的子字符串”中我們會詳細討論如何用遞歸分析問題并基于循環寫代碼。 除效率之外，遞歸還有可能引起更嚴重的問題：調用棧溢出。 #### 6.1.1 (10)斐波那契數列[?](https://blog.yorek.xyz/leetcode/code_interviews_1/#611-10 "Permanent link") > 寫一個函數，輸入n，求斐波那契（Fibonacci）數列的第n項。 **解法一：遞歸** ~~~ private long Fibonacci_Solution1(int n) { if (n == 0) return 0; else if (n == 1) return 1; else return Fibonacci_Solution1(n - 1) + Fibonacci_Solution1(n - 2); } ~~~ 這種解法有很嚴重的效率問題。我們以求解f(10)為例，可以得到下面的調用圖。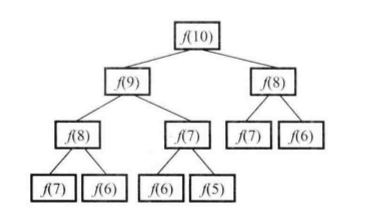  基于遞歸求斐波那契數列第10項的調用過程 我們不難發現，在這棵樹中有很多節點都是重復的，而且重復的節點數會隨著n的增大而急劇增加。 該算法時間復雜度是O(2^n) **解法二：循環** ~~~ private long Fibonacci_Solution2(int n) { int[] results = {0, 1}; if (n < 2) { return results[n]; } int a = results[0]; int b = results[1]; int result = 0; for (int i = 2; i <= n; i++) { result = a + b; a = b; b = result; } return result; } ~~~ 該算法時間復雜度是O(n) **解法三：利用數學公式** \\begin{bmatrix}f(n) & f(n-1) \\\\ f(n-1) & f(n-2)\\end{bmatrix}=\\begin{bmatrix}1 & 1 \\\\ 1 & 0\\end{bmatrix}^{n-1} 利用上面的公式，我們只需要求得矩陣\\begin{bmatrix}1 & 1 \\\\ 1 & 0\\end{bmatrix}^{n-1}即可得到f(n)。如果只是簡單地從0開始循環，n次方仍然需要n次運算，其時間復雜度還是O(n)，并不比前面的快。所以我們需要利用乘方的如下性質： a^n=\\begin{cases} a^{n/2} \\cdot a^{n/2}, & n為偶數 \\\\ a^{(n-1)/2} \\cdot a^{(n-1)/2} \\cdot a, & n為奇數 \\end{cases} 用上面的公式可以看出，我們想求n次方，就要先求n/2次方，在把n/2次方平方一下即可。這可以用遞歸的思路實現。 ~~~ private static class Matrix2By2 { long m_00; long m_01; long m_10; long m_11; Matrix2By2(long m_00, long m_01, long m_10, long m_11) { this.m_00 = m_00; this.m_01 = m_01; this.m_10 = m_10; this.m_11 = m_11; } static Matrix2By2 matrixMultiply(Matrix2By2 matrix1, Matrix2By2 matrix2) { return new Matrix2By2( matrix1.m_00 * matrix2.m_00 + matrix1.m_01 * matrix2.m_10, matrix1.m_00 * matrix2.m_01 + matrix1.m_01 * matrix2.m_11, matrix1.m_10 * matrix2.m_00 + matrix1.m_11 * matrix2.m_10, matrix1.m_10 * matrix2.m_01 + matrix1.m_11 * matrix2.m_11); } static Matrix2By2 MatrixPower(int n) { Matrix2By2 matrix; if (n == 1) { matrix = new Matrix2By2(1, 1, 1, 0); } else if (n % 2 == 0) { matrix = MatrixPower(n / 2); matrix = matrixMultiply(matrix, matrix); } else { // n % 2 == 1 matrix = MatrixPower((n - 1) / 2); matrix = matrixMultiply(matrix, matrix); matrix = matrixMultiply(matrix, new Matrix2By2(1, 1, 1, 0)); } return matrix; } } private long Fibonacci_Solution3(int n) { int[] results = {0, 1}; if (n < 2) { return results[n]; } Matrix2By2 matrix2By2 = Matrix2By2.MatrixPower(n - 1); return matrix2By2.m_00; } ~~~ 該算法時間復雜度是O(logn)，在第16題”數值的整數次方”中會討論這種算法。 相關題目 青蛙跳臺階問題：一只青蛙一次可以跳上1級臺階，也可以跳上2級臺階。求該青蛙跳上一個n級的臺階總共有多少種跳法。 相關題目 我們可以用2x1的小矩形橫著或者豎著去覆蓋更大的矩形。請問用8個2x1的小矩形無重疊地覆蓋一個2x8的大矩形有多少種覆蓋方法。 f(8)=f(7)+f(6)  一個2x1的矩形和2x8的矩形 上面兩個題目都是斐波那契數列的例子。 ### 6.2 查找和排序[?](https://blog.yorek.xyz/leetcode/code_interviews_1/#62 "Permanent link") 查找和排序都是在程序設計中經常用到的算法。查找相對而言較為簡單，不外乎順序查找、二分查找、哈希表查找和二叉排序樹查找。 **小提示** 如果要求在排序的數組或者部分排序的數組中查找一個數字或統計某個數字出現的次數，我們都可以嘗試用二分查找算法。 哈希表和二叉排序樹查找的重點在于考察對應的數據結構而不是算法。哈希表最主要的優點是能夠在O(1)時間內查找某一元素，是效率最高的查找方式；但其缺點是需要額外的空間實現哈希表。例如第50題“第一個只出現一次的字符”就是利用哈希表的特性來實現高效查找的。 與二叉排序樹查找算法對應的數據結構是二叉搜索樹。具體例子為第33題“二叉搜索樹的后序遍歷序列”和第36題“二叉搜索樹與雙向鏈表”。 排序與查找要復雜一點。我們需要知道插入排序、冒泡排序、歸并排序、快速排序等不同算法的優劣，能夠從額外空間消耗、平均時間復雜度和最差時間復雜度等方面去比較它們的優缺點。特別注意的是我們需要寫出快速排序的代碼。 實現快速排序算法的關鍵在于先在數組中選擇一個數字，接下來把數組中的數字分為兩部分，比選擇的數字小的數字移到數組左邊，比選擇的數字大的移到數組右邊。接下來可以用遞歸的思路分別對每次選中的數字的左右兩邊排序 ~~~ public class QuickSort { private static int partition(int[] numbers, int lo, int hi) { if (numbers == null || numbers.length == 0 || lo < 0 || hi >= numbers.length) { throw new IllegalArgumentException("Invalid params"); } int key = numbers[lo]; while (lo < hi) { // 比選擇的數字小的數字移到數組左邊 while (numbers[hi] >= key && hi > lo) { hi--; } numbers[lo] = numbers[hi]; // 比選擇的數字大的移到數組右邊 while (numbers[lo] <= key && hi > lo) { lo++; } numbers[hi] = numbers[lo]; } numbers[hi] = key; return hi; } public static void sort(int[] numbers, int lo, int hi) { if (lo >= hi) { return; } int index = partition(numbers, lo, hi); sort(numbers, lo, index - 1); sort(numbers, index + 1, hi); } public static void main(String[] args) { int[] numbers = {4, 3, 1, 5, 6, 10, 7, 6, 8}; sort(numbers, 0, numbers.length - 1); for (int num : numbers) { System.out.print(" " + num); } } } ~~~ 上面的`partition`除了可以用在快速排序中，還可以用來實現在長度為n的數組中查找第k大的數字，第39題“數組中出現次數超過一半的數字”和第40題“最小的k個數”都可以用這個函數來解決。 **插入排序** ~~~ public static void sort(Comparable[] a) { // 將a[]升序排列 int N = a.length; for (int i = 0; i < N; i++) { for (int j = i; j > 0 && AbsSort.less(a[j], a[j-1]); j--) { AbsSort.exch(a, j, j-1); } } } ~~~ **冒泡排序** ~~~ public static void sort(Comparable[] a){ // 將a[]升序排列 int N = a.length; for (int i = 0; i < N - 1; i++) { for (int j = 0; j < N - i - 1; j++) { if (AbsSort.less(a[j], a[j+1])) { AbsSort.exch(a, j, j+1); } } } } ~~~ **自頂向下歸并排序** ~~~ public class Merge extends AbsSort{ private static Comparable[] aux; // 歸并所需的輔助數組 public static void sort(Comparable[] a) { aux = new Comparable[a.length]; sort(a, 0, a.length - 1); } private static void sort(Comparable[] a, int lo, int hi) { if (hi <= lo) return; int mid = lo + (hi - lo)/2; sort(a, lo, mid); sort(a, mid+1, hi); merge(a, lo, mid, hi); } /** * 原地歸并 */ public static void merge(Comparable[] a, int lo, int mid, int hi) { int i = lo, j = mid+1; for (int k = lo; k <= hi; k++) aux[k] = a[k]; for (int k = lo; k <= hi; k++) { if (i > mid) a[k] = aux[j++]; else if (j > hi) a[k] = aux[i++]; else if (less(aux[j], aux[i])) a[k] = aux[j++]; else a[k] = aux[i++]; } } } ~~~ **自底向上的歸并排序** ~~~ public class MergeBU extends AbsSort{ private static Comparable[] aux; public static void sort(Comparable[] a) { int N = a.length; aux = new Comparable[N]; for (int sz = 1; sz < N; sz = sz+sz) // sz子數組大小 for (int lo = 0; lo < N-sz; lo += sz+sz) // lo:子數組索引 merge(a, lo, lo+sz-1, Math.min(lo+sz+sz-1, N-1)); } /** * 原地歸并 */ public static void merge(Comparable[] a, int lo, int mid, int hi) { int i = lo, j = mid+1; for (int k = lo; k <= hi; k++) aux[k] = a[k]; for (int k = lo; k <= hi; k++) { if (i > mid) a[k] = aux[j++]; else if (j > hi) a[k] = aux[i++]; else if (less(aux[j], aux[i])) a[k] = aux[j++]; else a[k] = aux[i++]; } } } ~~~ 以下是常見排序算法的總結： | 排序方法 | 時間復雜度（平均） | 時間復雜度（最壞) | 時間復雜度（最好) | 空間復雜度 | 穩定性 | | --- | --- | --- | --- | --- | --- | | 冒泡排序 | O(n^2) | O(n^2) | O(n) | O(1) | 穩定 | | 簡單選擇排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | 不穩定 | | 直接插入排序 | O(n^2) | O(n^2) | O(n) | O(1) | 穩定 | | 希爾排序 | O(n^{4/3}) | O(n^2) | O(n) | O(1) | 不穩定 | | 堆排序 | O(nlog n) | O(nlog n) | O(nlog n) | O(1) | 不穩定 | | 快速排序 | O(nlog n) | O(n^2) | O(nlog n) | O(log n) | 不穩定 | | 歸并排序 | O(nlog n) | O(nlog n) | O(nlog n) | O(n) | 穩定 | [Sorting algorithm](https://en.wikipedia.org/wiki/Sorting_algorithm) #### 6.2.1 (11)旋轉數組的最小數字[?](https://blog.yorek.xyz/leetcode/code_interviews_1/#621-11 "Permanent link") > 把一個數組最開始的若干個元素搬到數組的末尾，我們稱之為數組的旋轉。輸入一個遞增排序的數組的一個旋轉，輸出旋轉數組的最小元素。例如數組{3, 4, 5, 1, 2}為{1, 2, 3, 4, 5}的一個旋轉，該數組的最小值為1。 本題與[LC-81-Search in Rotated Sorted Array II](https://blog.yorek.xyz/leetcode/leetcode81-90/#81-search-in-rotated-sorted-array-ii)比較類似；且前者要找具體的值，本題找最小值。但是具體思維可以借鑒，這樣處理可以一般情況。 考慮到以下特殊情況：當下標為lo和hi的兩個數字相同的情況，當lo，mid，hi對應的數字都相等時，上面的算法認為此時最小的數字位于中間數字的前面。這可不一定。比如數組{1, 0, 1, 1, 1}和數組{1, 1, 1, 0, 1}都是增序數列{0, 1, 1, 1, 1}的一個旋轉數組。在這兩個數組中最小數字為別位于左右半區。所以上面的算法一定會失敗一種情況。因此，當lo，mid，hi對應的數字都相等時，我們必須采用順序查找。 具體算法如下： ~~~ int min(int[] numbers) { if (numbers == null) { throw new IllegalArgumentException("Invalid params"); } else if (numbers.length == 1) { return numbers[0]; } int lo = 0; int hi = numbers.length - 1; while (lo < hi) { int mid = (lo + hi) >> 1; // 當lo，mid，hi對應的數字都相等時，采用順序查找 if (numbers[lo] == numbers[mid] && numbers[mid] == numbers[hi]) { return minInOrder(numbers, lo, hi); } if (numbers[mid] > numbers[hi]) { // a[mid]>a[hi]，說明最小值在右邊，且肯定不會是a[mid]，因為a[mid]>a[hi]>=min lo = mid + 1; } else { // a[mid]<=a[hi]，最小值可能是mid，所以不能漏掉 hi = mid; } } return numbers[hi]; } private int minInOrder(int[] numbers, int start, int end) { int min = numbers[start]; for (int i = start + 1; i <= end; i++) { if (numbers[i] < min) { min = numbers[i]; return min; } } return min; } ~~~ ### 6.3 回溯法[?](https://blog.yorek.xyz/leetcode/code_interviews_1/#63 "Permanent link") 回溯法可以看成蠻力法的升級版，它從解決問題每一步的所有可能選項里系統地選擇出一個可行的解決方案。回溯法非常適合由多個步驟組成的問題，并且每個步驟都有很多選項。當我們在某一步選擇了其中一個選項時，就進入下一步，然后又面臨新的選項。我們就這樣重復選擇，直至到達最終的狀態。 用回溯法解決的問題的所有選項可以形象地用樹狀結構表示。在某一步有n個可能的選項，那么該步驟可以看成是樹狀結構中的一個節點，每個選項看成樹中節點連接線，經過這些連接線到達該節點的n個子節點。樹的葉節點對應著終結狀態。如果在葉節點的狀態滿足題目的約束條件，那么我們找到了一個可行的解決方案。 如果在葉節點的狀態不滿足約束條件，那么只好回溯到它的上一個節點在嘗試其他的選項。如果上一個節點所有可能的選項都已經試過，并且不能到達滿足約束條件的終結狀態，則再次回溯到上一個節點。如果所有節點的所有選項都已經嘗試過仍然不能到達滿足約束條件的終結狀態，則該問題無解。 通常回溯法適合用遞歸實現代碼。當我們到達某一個節點時，嘗試所有可能的選項并在滿足條件的前提下遞歸地抵達下一個節點。 #### 6.3.1 (12)矩陣中的路徑[?](https://blog.yorek.xyz/leetcode/code_interviews_1/#631-12 "Permanent link") > 請設計一個函數，用來判斷在一個矩陣中是否存在一條包含某字符串所有字符的路徑。路徑可以從矩陣中任意一格開始，每一步可以在矩陣中向左、右、上、下移動一格。如果一條路徑經過了矩陣的某一格，那么該路徑不能再次進入該格子。例如在下面的3×4的矩陣中包含一條字符串“bfce”的路徑（路徑中的字母用下劃線標出）。但矩陣中不包含字符串“abfb”的路徑，因為字符串的第一個字符b占據了矩陣中的第一行第二個格子之后，路徑不能再次進入這個格子。 A \\underline{B} T G \\\\ C \\underline{F} \\underline{C} S \\\\ J D \\underline{E} H 此題同[LC-79-Word Search](https://blog.yorek.xyz/leetcode/leetcode71-80/#79-word-search) 這是一個可以用回溯法解決的典型題。首先，在矩陣中任選一個格子ch作為路徑的起點。如果路徑上第i個字符剛好是ch，那么到相鄰的格子尋找路徑上的第i+1個字符。除矩陣邊界上的格子之外，其他格子都有4個相鄰的格子。重復這個過程，直到路徑上的所有字符都在矩陣中找到相應的位置。 由于回溯法的遞歸特性，路徑可以看成一個棧。當在矩陣中定位了路徑中前n個字符的位置之后，在與第n個字符對應的格子的周圍都沒有找到第n+1個字符，這時候只好在路徑上回到第n-1的字符，重新定位第n個字符。 由于路徑不能重復進入矩陣的格子，所以還需要定義和字符矩陣大小一樣的布爾值矩陣，用來識別路徑是否已經進入了某個格子。 ~~~ private int pathLength = 0; private boolean hasPath(String matrix, int rows, int cols, String str) { if (matrix == null || matrix.length() != rows * cols || str == null) { return false; } boolean[] visited = new boolean[matrix.length()]; pathLength = 0; for (int row = 0; row < rows; row++) { for (int col = 0; col < cols; col++) { if (hasPathInner(matrix, rows, cols, row, col, str, visited)) { return true; } } } return false; } private boolean hasPathInner( String matrix, int rows, int cols, int row, int col, String str, boolean[] visited ) { if (pathLength == str.length()) { return true; } boolean hasPath = false; if (row >= 0 && row < rows && col >= 0 && col < cols && matrix.charAt(row * cols + col) == str.charAt(pathLength) && !visited[row * cols + col]) { pathLength++; visited[row * cols + col] = true; hasPath = hasPathInner(matrix, rows, cols, row, col - 1, str, visited) || hasPathInner(matrix, rows, cols, row - 1, col, str, visited) || hasPathInner(matrix, rows, cols, row, col + 1, str, visited) || hasPathInner(matrix, rows, cols, row + 1, col, str, visited); if (!hasPath) { pathLength--; visited[row * cols + col] = false; } } return hasPath; } ~~~ #### 6.3.2 (13)機器人的運動范圍[?](https://blog.yorek.xyz/leetcode/code_interviews_1/#632-13 "Permanent link") > 地上有一個m行n列的方格。一個機器人從坐標(0, 0)的格子開始移動，它每一次可以向左、右、上、下移動一格，但不能進入行坐標和列坐標的數位之和大于k的格子。例如，當k為18時，機器人能夠進入方格(35, 37)，因為3+5+3+7=18。但它不能進入方格(35, 38)，因為3+5+3+8=19。請問該機器人能夠到達多少個格子？ 和前面的題目類似，這個方格也可以看成m\\times{n}的矩陣。同樣，在這個矩陣中，除邊界上的格子之外，其他格子都有4個相鄰的格子。 機器人從坐標(0, 0)開始移動，當它準備進入(i, j)的格子時，通過檢查坐標的位數來判斷機器人是否可以進入。如果能夠進入，則在判斷它能否進入4個相鄰的格子。因此，我們可以用如下的代碼來實現回溯算法： ~~~ private int movingCount(int threshold, int rows, int cols) { if (threshold < 0 || rows <= 0 || cols <= 0) { return 0; } boolean[] visited = new boolean[rows * cols]; return movingCountInner(threshold, rows, cols, 0, 0, visited); } private int movingCountInner(int threshold, int rows, int cols, int x, int y, boolean[] visited) { int index = rows * x + y; int count = 0; if (x >= 0 && x < cols && y >= 0 && y < rows && !visited[index] && isMatched(threshold, x, y)) { visited[index] = true; count = movingCountInner(threshold, rows, cols, x - 1, y, visited) + movingCountInner(threshold, rows, cols, x, y - 1, visited) + movingCountInner(threshold, rows, cols, x + 1, y, visited) + movingCountInner(threshold, rows, cols, x, y + 1, visited) + 1; } return count; } private boolean isMatched(int threshold, int x, int y) { int sum = 0; do { sum += x % 10; x /= 10; } while (x != 0); do { sum += y % 10; y /= 10; } while (y != 0); return sum <= threshold; } ~~~ ### 6.4 動態規劃與貪婪算法[?](https://blog.yorek.xyz/leetcode/code_interviews_1/#64 "Permanent link") 如果題目是求一個問題的最優解（通常是求最大值或者最小值），而且該問題能夠分解成若干個子問題，而且子問題之間還有重疊的更小的子問題，就可以考慮使用動態規劃來解決這個問題。 我們在應用動態規劃之前要分析能夠把大問題分解為小問題，分解后的每個小問題也存在最優解。如果把小問題的最優解組合起來能夠得到整個問題的最優解，那么我們可以應用動態規劃來解決這個問題。 例如第14題中，我們如何長度為n的繩子剪成若干段，使得得到的各段長度的乘積最大。這個問題的目標是求出各段繩子長度的乘積最大值，也就是**求一個問題的最優解**——這是可以應用動態規劃求解的問題的第一個特點。 我們把長度為n的繩子剪成若干段后得到的乘積最大值定義為函數f(n)。假設我們把第一刀減在長度為i(0< i < n)的位置，于是把繩子剪成了長度分別為i和n-i的兩段。我們想要得到整個問題的最優解f(n)，那么要同樣用最優化的方法把長度為i和n-i的兩段分別剪成若干段，使得它們各自剪出的每段繩子的長度乘積最大。也就是說**整體問題的最優解是依賴各個子問題的最優解**——這是可以應用動態規劃求解的問題的第二個特點。 **我們把大問題分解為若干個小問題，這些小問題之間還有相互重疊的更小的子問題**——這是可以應用動態規劃求解的問題的第三個特點。假設繩子最初的長度為10，我們可以把繩子剪成長度分別為4和6的兩段，也就是f(4)和f(6)都是f(10)的子問題。接下來分別求解這兩個子問題，我們可以把長度為4的繩子剪成均為2的兩段，即f(2)是f(4)的子問題。同樣，我們也可以把6剪成2和4的兩段，即f(2)和f(4)都是f(6)的子問題。我們注意到f(2)是f(4)和f(6)公共的更小的子問題。 由于子問題在分解大問題的過程中重復出現，為了避免重復求解子問題，我們可以用從下往上的順序先計算小問題的最優解并存儲下來，再以此為基礎求取大問題的最優解。**從上往下分析問題，從下往上求解問題**，這是可以應用動態規劃求解的問題的第四個特點。在大部分題目中，已解決的子問題的最優解都存儲在一維或者二維數組中。 在應用動態規劃時，我們每一步都可能面臨若干個選擇。在求解第14題時，我們在剪一刀的時候就有n-1個選擇。我們可以剪在任何位置，由于我們事先不知道剪在哪個位置是最優的解法，只好把所有的可能都嘗試一遍，然后得出最優的剪法。 貪婪算法和動態規劃不一樣。**當我們應用貪婪算法時，每一步都可以做出一個貪婪選擇，基于這個選擇，我們確定能夠得到最優解。為什么貪婪選擇能夠得到最優解，這是我們應用貪婪算法時都需要問的問題，需要用數學方式來證明貪婪選擇是正確的。** #### 6.4.1 (14)剪繩子[?](https://blog.yorek.xyz/leetcode/code_interviews_1/#641-14 "Permanent link") > 給你一根長度為n繩子，請把繩子剪成m段（m、n都是整數，n>1并且m≥1）。每段的繩子的長度記為k\[0\]、k\[1\]、……、k\[m\]。k\[0\]\*k\[1\]\*…\*k\[m\]可能的最大乘積是多少？例如當繩子的長度是8時，我們把它剪成長度分別為2、3、3的三段，此時得到最大的乘積18。 **解法一：動態規劃** ~~~ private int maxProductAfterCutting_solution1(int length) { if (length < 2) { return 0; } else if (length == 2) { return 1; } else if (length == 3) { return 2; } int[] products = new int[length + 1]; products[0] = 0; products[1] = 1; products[2] = 2; products[3] = 3; for (int i = 4; i <= length; i++) { int max = 0; for (int j = 1; j <= i / 2; j++) { int result = products[j] * products[i - j]; if (result > max) { max = result; } products[i] = max; } } return products[length]; } ~~~ 上述products中存儲的就是子問題的最優解。數組中第i個元素表示把長度為i的繩子剪成若干段之后各段長度乘積的最大值，即f(i)。注意，這是子問題的最優解，也就是說i是可以不進行切割的。 **解法二：貪婪算法** 我們按照如下的策略來剪繩子，則得到的各段繩子的長度的乘積最大：當n>=5時，我們盡可能多地剪長度為3的繩子；當剩下的繩子長度為4時，把繩子剪成兩段長度為2的繩子。 ~~~ private int maxProductAfterCutting_solution2(int length) { if (length < 2) { return 0; } else if (length == 2) { return 1; } else if (length == 3) { return 2; } // 盡可能多剪去長度為3的繩子段 int timesOf3 = length / 3; // 當繩子最后剩下的長度為4時，不能再減去長度為3的繩子段 if (length - timesOf3 * 3 == 1) { timesOf3--; } // 此時更好的方法是把繩子剪成長度為2的兩段，因為2x2>3x1 int timesOf2 = (length - timesOf3 * 3) / 2; return (int) Math.pow(3, timesOf3) * (int) Math.pow(2, timesOf2); } ~~~ 接下來我們證明這種思路的正確性。首先，當n>=5時，我們可以證明2(n-2)>n并且3(n-3)>n。也就是說，當繩子剩下的長度大于或者等于5的時候，我們就把它剪成長度為3或者2的繩子段。另外，當n>=5時，3(n-3)>=2(n-2)，因此我們應該盡量多剪長度為3的繩子段。 前面證明的前提是n>=5。那么當繩子的長度為4時，2x2>3x1，同時2x2=4，也就是說當繩子長度為4時其實沒必要剪，只是題目要求至少一刀。 ### 6.5 位運算[?](https://blog.yorek.xyz/leetcode/code_interviews_1/#65 "Permanent link") 位運算只有5種運算：與、或、異或、左移、右移。 與、或、異或運算的規律可以用下表總結： | 與(&) | 0 & 0 = 0 | 1 & 0 = 0 | 0 & 1 = 0 | 1 & 1 = 1 | | 或(|) | 0 | 0 = 0 | 1 | 0 = 1 | 0 | 1 = 1 | 1 | 1 = 1 | | 異或(^) | 0 ^ 0 = 0 | 1 ^ 0 = 1 | 0 ^ 1 = 1 | 1 ^ 1 = 0 | 左移運算符m<<n表示把m左移n位。在左移n位的時候，最左邊的n位會被丟棄，同時在最右邊補上n個0。比如： 00001010 << 2 = 00101000 10001010 << 3 = 01010000 右移運算符m>>n表示把m右移n位。在右移n位的時候，最右邊的n位將被丟棄。但右移時處理最左邊位的情形要稍微復雜一點。如果數字是一個無符號數值，則用0填補最左邊的n位；如果數字是一個有符號數值，則用數字的符號位填補最左邊的n位。也就是說，如果數字原先是一個正數，則右移之后再最左邊補n個0；如果數字原先是個負數，則右移之后再最左邊補n個1。下面是對兩個8位有符號數進行右移的例子： 00001010 >> 2 = 00000010 10001010 >> 3 = 11110001 ### 6.5.1 (15)二進制中1的個數[?](https://blog.yorek.xyz/leetcode/code_interviews_1/#651-151 "Permanent link") > 請實現一個函數，輸入一個整數，輸出該數二進制表示中1的個數。例如把9表示成二進制是1001，有2位是1。因此如果輸入9，該函數輸出2。 **解法一：常規解法** 先判斷整數二進制表示中最右邊一位是不是1；然后把輸入的整數右移一位，此時原來處于從右邊數起的第二位被移到最右邊了，再判斷它是不是1；這樣一直移動，直到整個整數變成0為止。現在的問題變成了怎么判斷一個整數的最右邊是不是1。這也很簡單，只需要把整數和1做位與運算看結果是不是0就知道了。 但是，如果輸入一個負數，比如0x80000000，則運行的時候會發生什么情況？當把負數0x80000000右移一位的時候，并不是簡單地把最高位的1移到第二位變成0x4000000，而是0xC000000。這是因為移位前是一個負數，仍然要保證移位后也是一個負數，因此移位后的最高位會設為1。如果一直做右移運算，那么最終這個數字就會變成0xFFFFFFFF而陷入死循環。 為了避免死循環，我們可以不右移輸入的數字n。而是左移一個flag。 ~~~ int NumberOf1_Solution1(int n) { int count = 0; int flag = 1; while (flag != 0) { if ((n & flag) != 0) { count++; } flag = flag << 1; } return count; } ~~~ **解法二：牛逼解法** 我們發現，把一個整數減去1，再和原整數做位與運算，會把該整數最右邊的1變成0。比如下面兩個例子 1100 -> (1011 & 1100) = 1000 -> 0 1010 -> (1001 & 1010) = 1000 -> 0 ~~~ int NumberOf1_Solution2(int n) { int count = 0; while (n != 0) { count++; n = (n - 1) & n; } return count; } ~~~ 相關題目 用一條語句判斷一個整數是不是2的整數次方。 *一個整數如果是2的整數次方，那么它的二進制位表示中有且只有一位是1，而其他所有位都是0。根據前面的分析，把這個整數減去1之后再和它自己做與運算，這個整數中唯一的1就會變成0* 相關題目 輸入兩個整數m和n，計算需要改變m的二進制表示中的多少位才能得到n。比如10的二進制表示為1010，13的二進制表示為1101，需要改變1010中的3位才能得到1101。 *我們可以分為兩步解決這個問題：第一步求這兩個數的異或；第二步統計異或結果中1的位數* 舉一反三 把一個整數減去1之后再和原來的整數做位與運算，得到的結果相當于把整數的二進制表示中最右邊的1變成0。很多二進制問題都可以用這種思路解決。 ### 7\. 總結[?](https://blog.yorek.xyz/leetcode/code_interviews_1/#7 "Permanent link") 數據結構題目一直是考查的重點。數組和字符串是兩種最基本的數據結構。鏈表是使用頻率最高的一種數據結構。如果想加大面試的難度，那么他很有可能會選用與樹相關的題目。由于棧和遞歸調用密切相關，隊列在圖（包括樹）的寬度優先遍歷中需要用到，因此也需要掌握這兩種數據結構。 算法是另一個重點。查找（特別是二分查找）和排序（特別是快速排序和歸并排序）是經常考查的算法。回溯法很適合解決迷宮以及類似的問題。如果需要求一個問題的最優2解，那么可以嘗試使用動態規劃。假如我們在用動態規劃分析問題時發現每一步都存在一個能得到最優解的選擇，那么可以嘗試使用貪婪算法。另外，我們還需要掌握分析時間復雜度的方法，理解即使同一思路，基于循環和遞歸的不同實現，它們的時間復雜度可能不大相同。很多時候我們會用自上而下的遞歸思路分析問題，卻會基于自下而上的循環實現代碼。 位運算是針對二進制數字的運算規律。只要熟練掌握了二進制的與、或、異或、左移、右移操作，就能解決相關問題。