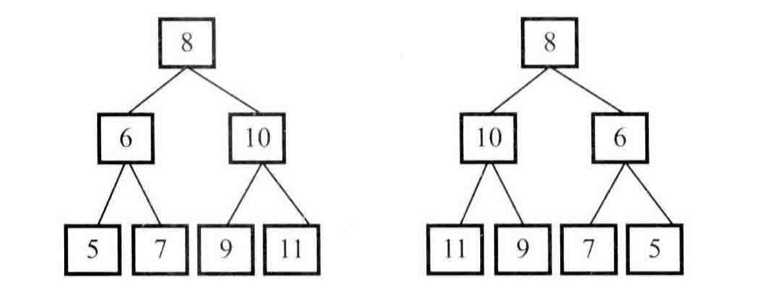
[TOC] ## 1\. 畫圖讓抽象問題形象化[?](https://blog.yorek.xyz/leetcode/code_interviews_4/#1 "Permanent link") ### 1.1 (27)二叉樹的鏡像[?](https://blog.yorek.xyz/leetcode/code_interviews_4/#11-27 "Permanent link") > 請完成一個函數，輸入一個二叉樹，該函數輸出它的鏡像。 二叉樹的鏡像的特點如下圖所示：  兩顆互為鏡像的二叉樹 我們可以看出一棵樹的鏡像是這么生成的：先前序遍歷這棵樹的每個節點，如果遍歷到的節點有子節點，就交換它的兩個子節點。當交換完所有非葉節點的左、右子節點之后，就得到了樹的鏡像。 ~~~ /** * 遞歸實現 */ public BinaryTreeNode mirrorRecursively(BinaryTreeNode root) { if (root == null) { return null; } if (root.left == null && root.right == null) { return root; } BinaryTreeNode left = root.left; root.left = root.right; root.right = left; if (root.left != null) { mirrorRecursively(root.left); } if (root.right != null) { mirrorRecursively(root.right); } return root; } /** * 循環實現 */ public BinaryTreeNode mirrorIteratively(BinaryTreeNode root) { if (root == null) { return null; } Stack<BinaryTreeNode> stack = new Stack<>(); stack.push(root); while (!stack.isEmpty()) { BinaryTreeNode node = stack.pop(); BinaryTreeNode temp = node.left; node.left = node.right; node.right = temp; if (node.left != null) { stack.push(node.left); } if (node.right != null) { stack.push(node.right); } } return root; } ~~~ ### 1.2 (28)對稱的二叉樹[?](https://blog.yorek.xyz/leetcode/code_interviews_4/#12-28 "Permanent link") > 請實現一個函數，用來判斷一棵二叉樹是不是對稱的。如果一棵二叉樹和它的鏡像一樣，那么它是對稱的。 此題同[LC-101-Symmetric Tree](https://blog.yorek.xyz/leetcode/leetcode101-110/#101-symmetric-tree) 在下圖所示的3棵樹中，第一棵二叉樹是對稱的，另外兩棵不是。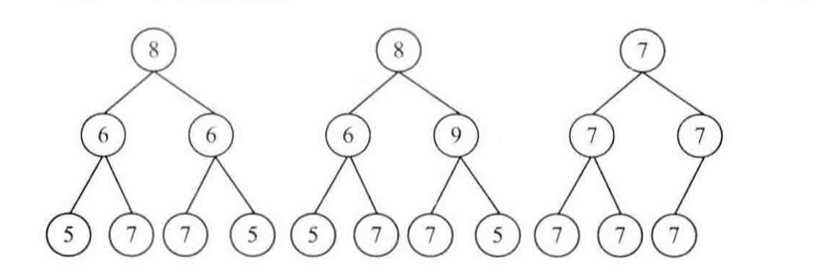  第一棵是對稱的，另外兩棵不是 我們可以先比較根節點，然后遞歸比較左子樹的左節點與右子樹的右節點、左子樹的右節點與右子樹的子節點。 ~~~ public boolean isSymmetrical(BinaryTreeNode root) { return isSymmetrical(root, root); } private boolean isSymmetrical(BinaryTreeNode root1, BinaryTreeNode root2) { if (root1 == null && root2 == null) { return true; } if (root1 == null || root2 == null) { return false; } if (root1.value != root2.value) { return false; } return isSymmetrical(root1.left, root2.right) && isSymmetrical(root1.right, root2.left); } ~~~ ### 1.3 (29)順時針打印矩陣[?](https://blog.yorek.xyz/leetcode/code_interviews_4/#13-29 "Permanent link") > 輸入一個矩陣，按照從外向里以順時針的順序依次打印出每一個數字 例如輸入如下矩陣，依次打印出數字1 2 3 4 8 12 16 15 14 13 9 5 6 7 11 10  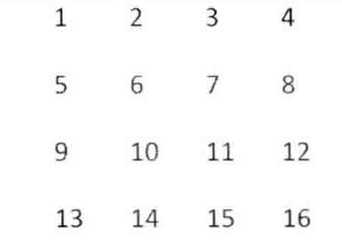此題同[LC-54-Spiral Matrix](https://blog.yorek.xyz/leetcode/leetcode51-60/#54-spiral-matrix) 這道題完全沒有涉及復雜的數據結構或者高級的算法，看起來是一個很簡單的問題。但實際上解決這個問題時會在代碼中包含多個循環，而且需要判斷多個邊界條件。 總體上來說，我們可以每次循環打印一圈。循環可以開始的條件是`columns > start * 2 && rows > start * 2`。 在每次循環中，要判斷除第一條邊之外的三條邊是否可以打印，以及打印時循環開始、結束的值。 ~~~ private void printMatrixClockwisely(int[][] numbers, int columns, int rows) { if (numbers == null || columns <= 0 || rows <= 0) { return; } int start = 0; while (columns > start * 2 && rows > start * 2) { printMatrixInCircle(numbers, columns, rows, start); start++; } } private void printMatrixInCircle(int[][] numbers, int columns, int rows, int start) { int endX = columns - 1 - start; int endY = rows - 1 - start; // 從左到右打印一行 for (int i = start; i <= endX; i++) { int number = numbers[start][i]; System.out.printf("%d\t", number); } // 從上到下打印一列 if (start < endY) { for (int i = start + 1; i <= endY; i++) { int number = numbers[i][endX]; System.out.printf("%d\t", number); } } // 從右到左打印一行 if(start < endX && start < endY) { for(int i = endX - 1; i >= start; i--) { int number = numbers[endY][i]; System.out.printf("%d\t", number); } } // 從下到上打印一行 if(start < endX && start < endY - 1) { for(int i = endY - 1; i >= start + 1; i--) { int number = numbers[i][start]; System.out.printf("%d\t", number); } } } ~~~ ## 2\. 舉例讓抽象問題具體化[?](https://blog.yorek.xyz/leetcode/code_interviews_4/#2 "Permanent link") ### 2.1 (30)包含min函數的棧[?](https://blog.yorek.xyz/leetcode/code_interviews_4/#21-30min "Permanent link") > 定義棧的數據結構，請在該類型中實現一個能夠得到棧的最小元素的min函數。在該棧中，調用min、push及pop的時間復雜度都是O(1)。 我們可以在棧的內部額外使用一個輔助棧，棧中同步保存每次進棧操作時棧中最小值。 ~~~ class StackWithMin<E extends Comparable> extends Stack<E> { // 輔助棧 private Stack<E> minStack = new Stack<>(); public synchronized E min() { return minStack.peek(); } @Override public synchronized E pop() { minStack.pop(); return super.pop(); } @Override public synchronized E peek() { return super.peek(); } @Override public E push(E item) { if (minStack.isEmpty() || minStack.peek().compareTo(item) > 0) { minStack.push(item); } else { minStack.push(minStack.peek()); } return super.push(item); } } ~~~ ### 2.2 (31)棧的壓入、彈出序列[?](https://blog.yorek.xyz/leetcode/code_interviews_4/#22-31 "Permanent link") > 輸入兩個整數序列，第一個序列表示棧的壓入順序，請判斷第二個序列是否為該棧的彈出順序。假設壓入棧的所有數字均不相等。例如序列1、2、3、4、5是某棧的壓棧序列，序列4、5、3、2、1是該壓棧序列對應的一個彈出序列，但4、3、5、1、2就不可能是該壓棧序列的彈出序列。 我們可以找到判斷一個序列是不是棧的彈出序列的規律：如果下一個彈出的數字剛好是棧頂數字，那么直接彈出；如果下一個彈出的數字不在棧頂，則把壓棧序列中還沒有入棧的數字壓入輔助棧，直到把下一個需要彈出的數字壓入棧頂為止；如果所有數字都壓入棧后仍然沒有找到下一個彈出的數字，那么該序列不可能是一個序列。 ~~~ private boolean isPopOrder(int[] push, int[] pop) { if (push == null || pop == null || push.length != pop.length) { return false; } final int length = pop.length; boolean possible = false; int pushIndex = 0; int popIndex = 0; Stack<Integer> stack = new Stack<>(); while (popIndex < length) { // 當輔助棧的棧頂元素不是要彈出的元素 // 先壓入一些數字入棧 while (stack.isEmpty() || stack.peek() != pop[popIndex]) { // 如果所有數字都壓入輔助棧了，退出循環 if (pushIndex == length) { break; } stack.push(push[pushIndex]); pushIndex++; } if (stack.peek() != pop[popIndex]) break; stack.pop(); popIndex++; } if (stack.isEmpty() && popIndex == length) { possible = true; } return possible; } ~~~ ### 2.3 (32)從上到下打印二叉樹[?](https://blog.yorek.xyz/leetcode/code_interviews_4/#23-32 "Permanent link") #### 2.3.1 不分行從上到下打印二叉樹[?](https://blog.yorek.xyz/leetcode/code_interviews_4/#231 "Permanent link") > 從上往下打印出二叉樹的每個結點，同一層的結點按照從左到右的順序打印。 該題就是一個二叉樹的層序遍歷問題。 ~~~ private void printFromTopToBottom(BinaryTreeNode root) { if (root == null) { return; } Queue<BinaryTreeNode> queue = new LinkedList<>(); queue.offer(root); while (!queue.isEmpty()) { BinaryTreeNode node = queue.poll(); System.out.printf("%d\t", node.value); if (node.left != null) { queue.offer(node.left); } if (node.right != null) { queue.offer(node.right); } } } ~~~ 本題擴展 如何廣度優先遍歷一副有向圖？同樣也可以基于隊列實現。樹是圖的一種特殊退化形式，從上到下按層遍歷二叉樹，從本質上來說就是廣度優先遍歷二叉樹。 舉一反三 不管廣度優先遍歷一副有向圖還是一棵樹，都要用到隊列。首先把起始節點(對樹而言是根節點)放入隊列。接下來每次從隊列的頭部取出一個節點，遍歷這個節點之后就把它能達到的節點(對樹而言是子節點)都依次放入隊列。重復這個遍歷過程，直到隊列中的節點全部被遍歷為止。 #### 2.3.2 分行從上到下打印二叉樹[?](https://blog.yorek.xyz/leetcode/code_interviews_4/#232 "Permanent link") > 從上到下按層打印二叉樹，同一層的結點按從左到右的順序打印，每一層打印到一行。 此題同[LC-102-Binary Tree Level Order Traversal](https://blog.yorek.xyz/leetcode/leetcode101-110/#102-binary-tree-level-order-traversal) 在前面代碼的基礎上額外加兩個變量：一個表示在當前層中還沒有打印的節點數；另一個變量表示下一層節點的數目 ~~~ private void print(BinaryTreeNode root) { if (root == null) { return; } Queue<BinaryTreeNode> queue = new LinkedList<>(); queue.offer(root); int nextLevel = 0; int toBePrinted = 1; while (!queue.isEmpty()) { BinaryTreeNode node = queue.poll(); System.out.printf("%d\t", node.value); if (node.left != null) { queue.offer(node.left); nextLevel++; } if (node.right != null) { queue.offer(node.right); nextLevel++; } toBePrinted--; if (toBePrinted == 0) { System.out.println(); toBePrinted = nextLevel; nextLevel = 0; } } } ~~~ 在上面的代碼中toBePrinted表示在當前層中還沒有打印的節點數，而變量nextLevel表示下一層的節點。 #### 2.3.3 之字形打印二叉樹[?](https://blog.yorek.xyz/leetcode/code_interviews_4/#233 "Permanent link") > 請實現一個函數按照之字形順序打印二叉樹，即第一行按照從左到右的順序打印，第二層按照從右到左的順序打印，第三行再按照從左到右的順序打印，其他行以此類推。 此題同[LC-103-Binary Tree Zigzag Level Order Traversal](https://blog.yorek.xyz/leetcode/leetcode101-110/#103-binary-tree-zigzag-level-order-traversal) 按之字形順序打印二叉樹需要兩個棧。我們在打印某一層節點時，把下一層的子節點保存在對應的棧中。如果當前打印的是奇數層，則先保存左子節點再保存右子節點到第一個棧里；如果當前打印的是偶數層，則先保存右子節點再保存左子節點到第二個棧里。 ~~~ private void print(BinaryTreeNode root) { if (root == null) { return; } Stack<BinaryTreeNode>[] level2 = new Stack[2]; level2[0] = new Stack<>(); level2[1] = new Stack<>(); int current = 0; int next = 1; level2[current].push(root); while (!level2[0].isEmpty() || !level2[1].isEmpty()) { BinaryTreeNode node = level2[current].pop(); System.out.printf("%d ", node.value); if (current == 0) { if (node.left != null) { level2[next].push(node.left); } if (node.right != null) { level2[next].push(node.right); } } else { if (node.right != null) { level2[next].push(node.right); } if (node.left != null) { level2[next].push(node.left); } } if (level2[current].empty()) { System.out.println(); current = 1 - current; next = 1 - next; } } } ~~~ ### 2.4 (33)二叉搜索樹的后序遍歷序列[?](https://blog.yorek.xyz/leetcode/code_interviews_4/#24-33 "Permanent link") > 輸入一個整數數組，判斷該數組是不是某二叉搜索樹的后序遍歷的結果。如果是則返回true，否則返回false。假設輸入的數組的任意兩個數字都互不相同。 根據二叉搜索樹的特征以及樹的后序遍歷序列特征，我們可以寫出下面的代碼： ~~~ private boolean verifySequenceOfBST(int[] sequence) { if (sequence == null || sequence.length == 0) { return false; } return verifySequenceOfBSTInner(sequence, 0, sequence.length - 1); } private boolean verifySequenceOfBSTInner(int[] sequence, int start, int end) { final int n = sequence.length; int root = sequence[n - 1]; // 在二叉搜索樹中左子樹的結點小于根結點 int i = start; for (; i < end - 1; i++) { if (sequence[i] > root) break; } // 在二叉搜索樹中右子樹的結點大于根結點 int j = i; for(; j < end - 1; ++ j) { if(sequence[j] < root) return false; } // 判斷左子樹是不是二叉搜索樹 boolean left = true; if (i > start) left = verifySequenceOfBSTInner(sequence, start, i - 1); // 判斷右子樹是不是二叉搜索樹 boolean right = true; if (i < end) right = verifySequenceOfBSTInner(sequence, i, end - 1); return left && right; } ~~~ 相關題目 輸入一個整數數組，判斷該數組是不是某二叉搜索樹的前序遍歷結果。 *這和前面問題的后序遍歷很類似，只是在前序遍歷得到的序列中，第一個數字是根節點的值。* 舉一反三 如果面試題要求處理一顆二叉樹的遍歷序列，則可以先找到二叉樹的根節點，再基于根節點把整棵樹的遍歷序列拆分成左子樹對應的子序列和右子樹對應的子序列，接下來再遞歸地處理這兩個子序列。本題和第七題“重建二叉樹”應用的也是這種思路。 ### 2.5 (34)二叉樹中和為某一值的路徑[?](https://blog.yorek.xyz/leetcode/code_interviews_4/#25-34 "Permanent link") > 輸入一棵二叉樹和一個整數，打印出二叉樹中結點值的和為輸入整數的所有路徑。從樹的根結點開始往下一直到葉結點所經過的結點形成一條路徑。 在樹的前中后序遍歷方式中，只有前序遍歷是首先訪問根節點的。 當用前序遍歷的方式訪問到某一節點時，我們把該節點添加到路徑上，并累加該節點的值。如果當前節點不是葉節點，則繼續訪問它的子節點。如果該節點為葉節點，并且路徑中節點值和剛好等于輸入的整數，則當前路徑符合要求，我們打印出來。當前節點訪問結束后，遞歸函數自動回到它的父節點。因此，我們在函數退出之前要把路徑上刪除當前節點并減去當前節點的值，以確保父節點時路徑剛好是從根節點到父節點。我們不難看出保存路徑的數據結構是一個棧，因為路徑要與遞歸調用狀態一致，而遞歸調用的本質就是一個壓棧和出棧的過程。 這里我們并沒有使用Stack而是一個List，因為Stack只能得到棧頂元素，而我們打印路徑的時候需要得到路徑上的所有節點，因此在代碼實現的時候Stack不是最好的選擇。 ~~~ private int currentSum = 0; private void findPath(BinaryTreeNode root, int expectedSum) { if (root == null) { return; } currentSum = 0; findPath(root, expectedSum, new ArrayList<>()); } private void findPath(BinaryTreeNode root, int expectedSum, List<Integer> path) { currentSum += root.value; path.add(root.value); // 如果是葉結點，并且路徑上結點的和等于輸入的值 // 打印出這條路徑 boolean isLeaf = root.left == null && root.right == null; if (isLeaf && expectedSum == currentSum) { System.out.print("A path is found: "); for (Integer node: path) { System.out.printf("%d\t", node); } System.out.println(); } // 如果不是葉結點，則遍歷它的子結點 if (root.left != null) { findPath(root.left, expectedSum, path); } if (root.right != null) { findPath(root.right, expectedSum, path); } // 在返回到父結點之前，在路徑上刪除當前結點， // 并在currentSum中減去當前結點的值 currentSum -= root.value; path.remove(path.size() - 1); } ~~~ ## 3\. 分解讓復雜問題簡單化[?](https://blog.yorek.xyz/leetcode/code_interviews_4/#3 "Permanent link") 我們遇到復雜的大問題時，如果能夠先把大問題分解成若干的簡單小問題，然后再逐個解決這些小問題，則可能也會容易很多。 在計算機領域有一類算法叫分治法，即“分而治之”，采用的就是各個擊破的思想。我們把分解之后的小問題各個解決，然后把小問題的解決方案結合起來解決大問題。 ### 3.1 (35)復雜鏈表的復制[?](https://blog.yorek.xyz/leetcode/code_interviews_4/#31-35 "Permanent link") > 請實現函數ComplexListNode clone(ComplexListNode head)，復制一個復雜鏈表。在復雜鏈表中，每個結點除了有一個next指針指向下一個結點外，還有一個sibling指向鏈表中的任意結點或者null。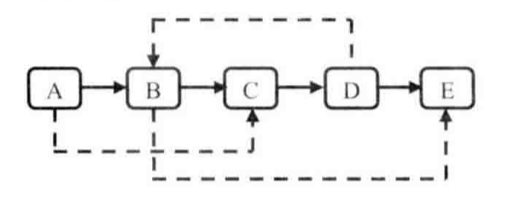  一個含有5個節點的復雜鏈表 **解法一：笨方法** 首先復制原始鏈表上的每個節點，并用next鏈接起來；然后設置每個節點的sibling指針。 對于一個含有n個節點的鏈表，由于定位每個節點的sibling都需要從鏈表頭節點開始經過O(n)步才能找到，因此這種方法總的時間復雜度是O(n^2)。 **解法二：空間換時間** 上述方法的時間主要花費在定位節點的sibling上面，我們試著在方面去進行優化。 我們還是分為兩步：第一步仍然是復制原始鏈表上的每個節點N創建N'，然后把每個節點N用next鏈接起來，同時把的配對信息放到一個哈希表中； 第二步還是設置復制鏈表的sibling。如果在原始鏈表中節點N的sibling指向節點S，那么在復制鏈表中，對應的N'應該指向S'。由于有了哈希表，我們可以用O(1)的時間根據S找到S'。 這種方法相當于用空間換時間。該方法時間復雜度為O(n)，空間復雜度也為O(n)。 **解法三：不用輔助空間的情況下實現O(n)的時間效率** 第一步仍然是根據原始鏈表的每個節點N創建對應的N'。這一次，我們把N'鏈接到N的后面。例子中的鏈表經過這一步之后的結構如下所示：  復制復雜鏈表的第一步 第二步設置復制出來的節點的sibling。假設原始鏈表上的N的sibling指向節點S，那么其對應復制出來的N'是N的next指向的節點，同樣S'也是S的next指向的節點。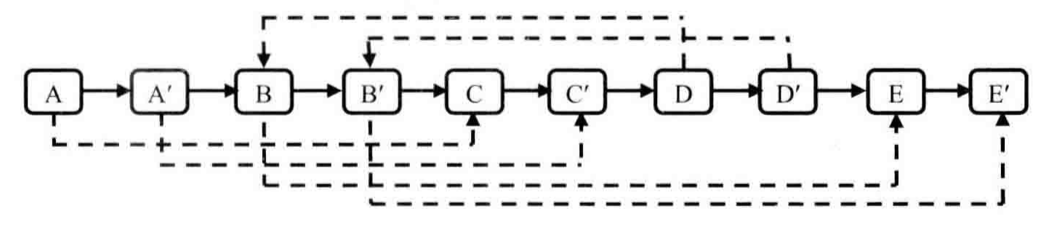設置sibling之后的鏈表如圖所示：  復制復雜鏈表的第二步 *注：如果原始鏈表上的節點N的sibling指向S，則其復制節點N'的sibling指向S的復制節點S'。* 第三步把這個長鏈表拆分為兩個鏈表：奇數、偶數位置分別是原始鏈表和復制出來的鏈表。  復制復雜鏈表的第三步 *注：把第二步得到的鏈表拆分成為兩個鏈表，奇數位置上的節點組成原始鏈表，偶數位置上的節點組成復制出來的節點。* ~~~ ComplexListNode clone(ComplexListNode head) { cloneNodes(head); connectSiblingNodes(head); return reconnectNodes(head); } private void cloneNodes(ComplexListNode head) { ComplexListNode node = head; while (node != null) { ComplexListNode cloned = new ComplexListNode(node.value); ComplexListNode.buildNodes(cloned, node.next, node.sibling); node.next = cloned; node = cloned.next; } } private void connectSiblingNodes(ComplexListNode head) { ComplexListNode node = head; while (node != null) { ComplexListNode cloned = node.next; if (node.sibling != null) { cloned.sibling = node.sibling.next; } node = cloned.next; } } private ComplexListNode reconnectNodes(ComplexListNode head) { ComplexListNode node = head; ComplexListNode clonedHead = null; ComplexListNode clonedNode = null; if (node != null) { clonedHead = clonedNode = node.next; node.next = clonedHead.next; node = node.next; } while (node != null) { clonedNode.next = node.next; clonedNode = clonedNode.next; node.next = clonedNode.next; node = node.next; } return clonedHead; } ~~~ ComplexListNode輔助代碼如下： ~~~ private static class ComplexListNode { int value; ComplexListNode next; ComplexListNode sibling; ComplexListNode(int value) { this.value = value; } static void buildNodes(ComplexListNode node, ComplexListNode next, ComplexListNode sibling) { if (node != null) { node.next = next; node.sibling = sibling; } } static void printList(ComplexListNode head) { ComplexListNode node = head; while(node != null) { System.out.printf("The value of this node is: %d.\n", node.value); if(node.sibling != null) System.out.printf("The value of its sibling is: %d.\n", node.sibling.value); else System.out.print("This node does not have a sibling.\n"); System.out.println(); node = node.next; } } } ~~~ ### 3.2 (36)二叉搜索樹與雙向鏈表[?](https://blog.yorek.xyz/leetcode/code_interviews_4/#32-36 "Permanent link") > 輸入一棵二叉搜索樹，將該二叉搜索樹轉換成一個排序的雙向鏈表。要求不能創建任何新的結點，只能調整樹中結點指針的指向。 如下圖所示，左邊的二叉搜索樹經過轉換之后變成右邊的排序雙向鏈表。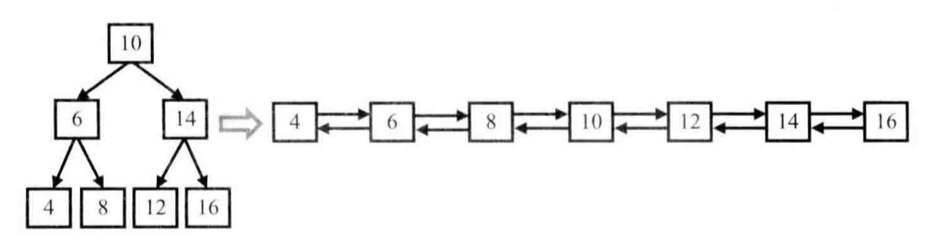  一顆二叉搜索樹及轉換之后的排序雙向鏈表 ~~~ private BinaryTreeNode last; private BinaryTreeNode convert(BinaryTreeNode root) { if (root == null || (root.left == null && root.right == null)) { return root; } last = null; convertNode(root); while (last != null && last.left != null) { last = last.left; } return last; } private void convertNode(BinaryTreeNode node) { if (node == null) { return; } BinaryTreeNode current = node; if (current.left != null) { convertNode(current.left); } current.left = last; if (last != null) { last.right = current; } last = current; if (node.right != null) { convertNode(node.right); } } ~~~ 在上面的代碼中，我們用last指向已經轉換好的鏈表的最后一個節點。當我們遍歷到10的節點時，它的左子樹都已經轉換好了，因此last指向值為8的節點。接著把根節點鏈接到鏈表后，值為10的節點成了鏈表中的最后一個節點（新的值最大的節點），于是last指向了這個值為10的節點。接下來遞歸遍歷右子樹。我們把右子樹中最左邊的子節點，并把該節點和值為10的節點鏈接起來。 ### 3.3 (37)序列化二叉樹[?](https://blog.yorek.xyz/leetcode/code_interviews_4/#33-37 "Permanent link") > 請實現兩個函數，分別用來序列化和反序列化二叉樹。 如果二叉樹的序列化是從根節點開始的，那么相應的反序列化在根節點的數值讀出來的時候就可以開始了。因此，我們可以根據前序遍歷的順序來序列化二叉樹，因為前序遍歷是從根節點開始的。在遍歷二叉樹碰到空指針時，將這些空指針序列化為一個特殊的字符（如'$'）。這樣就填滿成為一個滿二叉樹了。 例如，下面的二叉樹被序列化成為字符串“1,2,4,,,,3,5,,,6,,$”。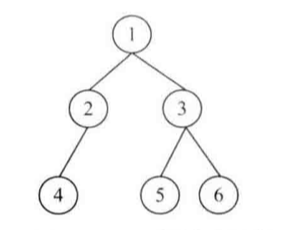  一顆被序列化成字符串“1,2,4,,,,3,5,,,6,,$”的二叉樹 ~~~ private String serialize(BinaryTreeNode root) { StringBuilder stream = new StringBuilder(); serializeInner(root, stream); return stream.toString(); } private void serializeInner(BinaryTreeNode root, StringBuilder stream) { if (root == null) { stream.append("$,"); return; } stream.append(root.value).append(","); serializeInner(root.left, stream); serializeInner(root.right, stream); } private int index = 0; private BinaryTreeNode deserialize(String stream) { if (stream == null || stream.isEmpty()) { return null; } String[] chars = stream.split(","); index = 0 ; return deserializeInner(chars); } private BinaryTreeNode deserializeInner(String[] chars) { if (chars[index].equals("$")) { index++; return null; } BinaryTreeNode node = new BinaryTreeNode(Integer.parseInt(chars[index++])); node.left = deserializeInner(chars); node.right = deserializeInner(chars); return node; } ~~~ 總結序列化和反序列化的過程，就會發現我們都是把二叉樹分解為3部分：根節點、左子樹和右子樹。我們在處理它的根節點之后再分別處理它的左右子樹。這就是典型的把問題遞歸分解然后逐個解決的過程。 ### 3.4 (38)字符串的排列[?](https://blog.yorek.xyz/leetcode/code_interviews_4/#34-38 "Permanent link") > 輸入一個字符串，打印出該字符串中字符的所有排列。例如輸入字符串abc，則打印出由字符a、b、c所能排列出來的所有字符串abc、acb、bac、bca、cab和cba。 我們可以考慮把這個復雜問題分解成小的問題。比如，我們把第一個字符串看成由兩部分組成：第一部分是它的第一個字符；第二部分是后面的所有字符。 我們求整個字符串的排列，可以看成兩步。第一步求所有可能出現在第一個位置的字符，即把第一個字符和后面所有的字符交換。第二步固定第一個字符，求后面所有字符的排列。這時候我們仍然把后面的所有字符分為兩部分：后面字符的第一個字符，以及這個字符之后的所有字符。然后把第一個字符逐一和它后面的字符交換。這就是典型的遞歸思路。 此題同[LC-46-Permutations](https://blog.yorek.xyz/leetcode/leetcode41-50/#46-permutations) ~~~ private void permutation(String str) { if (str == null) { return; } permutationInner(str.toCharArray(), 0); } private void permutationInner(char[] str, int begin) { if (begin == str.length - 1) { System.out.println(str); } else { for (int i = begin; i < str.length; i++) { // TODO swap method char temp = str[begin]; str[begin] = str[i]; str[i] = temp; permutationInner(str, begin + 1); // TODO swap method temp = str[begin]; str[begin] = str[i]; str[i] = temp; } } } ~~~ 本題擴展 如果不是求字符的所有排列，而是求字符的所有組合，應該怎么辦呢？ 還是輸入個字符a、b、c，則它們的組合有a、b、c、ab、ac、bc、abc。當交換字符串中的兩個字符時，雖然能得到兩個不同的排列，但卻是同一個組合。比如ab和ba是不同的排列，但只算一個組合。 如果輸入n個字符，則這n個字符能構成長度為1,2,...,n的組合。在求n個字符的長度為m（1≤m≤n）的組合的時候，我們把這n個字符分成兩部分:第一個字符和其余的所有字符。如果組合里包含第一個字符，則下一步在剩余的字符里選取m-1個字符；如果組合里不包含第一個字符，則下一步在剩余的n-1個符里選取m個字符。也就是說，我們可以把求n個字符組成長度為m的組合的問題分解成兩個子問題，分別求n-1個字符中長度為m-1的組合，以及求n-1個字符中長度為m的組合。這兩個子問題都可以用遞歸的方式解決。 相關題目 輸入一個含有8個數字的數組，判斷有沒有可能把這8個數字分別放到正方體的8個頂點上，使得正方體上三組相對的面上的4個頂點的和都相等。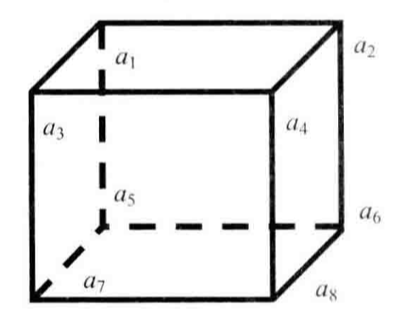 *這相當于先得到a1到a8這8個數字的所有排列，然后判斷有沒有某一個排列符合題目給定的條件，即a1+a2+a3+a4=a5+a6+a7+a8, a1+a3+a5+a7=a2+a4+a6+a8, a1+a2+a5+a6=a3+a4+a7+a8*  把8個數字放到正方體的8個頂點上 相關題目 在8x8的國際象棋上擺放8個皇后，使其不能相互攻擊，即任意兩個皇后不得處在同一行、同一列或者同一條對角線上。圖中的每個黑色格子表示一個皇后，這就是一種符合條件的擺放方法。請問總共有多少種符合條件的擺法？ *由于8個皇后的任意兩個不能處在同一行，那么肯定是每一個皇后占據一行。于是我們可以定義一個數組ColumnIndex\[8\]，數組中第i個數字表示位于第i行的皇后的列號。先把數組ColumnIndex的8個數字分別用0~7初始化，然后對數組ColumnIndex進行全排列。因為我們用不同的數字初始化數組，所以任意兩個皇后肯定不同列。只需判斷每一個排列對應的8個皇后是不是在同一條對角線上，也就是對于數組的兩個下標i和j，是否有i-j=ColumnIndex\[i\]-ColumnIndex\[j\]或者j-i=ColumnIndex\[i\]-ColumnIndex\[i\]*  8皇后問題