[TOC] ## 1\. 代碼的完整性[?](https://blog.yorek.xyz/leetcode/code_interviews_3/#1 "Permanent link") * 從三個方面確保代碼的完整性 通常我們可以從功能測試、邊界測試和負面測試3個方面設計測試用例 * 3種錯誤處理方式 1. 函數返回值 2. 設置全局變量 3. 拋異常 下表是上述3種錯誤處理方式的優缺點： | | 優點 | 缺點 | | --- | --- | --- | | 返回值 | 和系統API一致 | 不能方便地使用計算結果 | | 全局變量 | 能夠方便地使用計算結果 | 用戶可能忘記檢查全局變量 | | 異常 | 可以為不同的出錯原因定義不同的異常類型，邏輯清晰明了 | 有些語言不支持異常，拋出異常時對性能有負面影響 | ### 1.1 (16)數值的整數次方[?](https://blog.yorek.xyz/leetcode/code_interviews_3/#11-16 "Permanent link") > 實現函數double Power(double base, int exponent)，求base的exponent次方。不得使用庫函數，同時不需要考慮大數問題。 與[LC-50-Pow(x, n)](https://blog.yorek.xyz/leetcode/leetcode41-50/#50-powx-n)類似。 不過LeetCode上需要注意n的溢出問題。 此題看起來簡單，但卻有一些情況需要考慮到。 首先需要考慮到指數為0或負數的情況。當指數為負數時，可以先對指數求絕對值，算出結果之后再取倒數。在求倒數的時候，如果底數是0怎么辦，如何告訴函數的調用者出現了這種錯誤。 最后需要指出的是，由于0的0次方在數學上是沒有意義的，因此無論輸出是0還是1都是可以接受的，但這需要和面試官說清楚，表明我們已經考慮到這個邊界值了。 全面的解法如下： ~~~ private boolean invalidInput; private double power(double base, int exponent) { invalidInput = false; if (exponent < 0 && base == 0) { invalidInput = true; return 0; } long absExponent = Math.abs(exponent * 1L); double result = powerInner(base, absExponent); return exponent < 0 ? 1.0 / result : result; } private double powerInner(double base, long exponent) { double result = 1.0; for (int i = 1; i <= exponent; i++) { result *= base; } return result; } ~~~ 在上面的代碼中，我們采用全部變量來標識是否出錯了。如果出錯了，則返回的值是0。但為了區分是出錯的時候返回的0，還是底數為0的時候正常運行的0，我們定義了一個全局變量`invalidInput`。當出錯的時候，這個變量被設為true，否則為false。 **全面且高效的解法** 如果輸入的指數為32，我們需要在循環中做32次乘法。但我們可以考慮換一種思路：利用如下公式求a的n次方： a^n=\\begin{cases} a^{n/2} \\cdot a^{n/2}, & n為偶數 \\\\ a^{(n-1)/2} \\cdot a^{(n-1)/2} \\cdot a, & n為奇數 \\end{cases} 我們在介紹用O(logn)時間求斐波那契數列時討論過這個公式，這個公式很容易通過遞歸實現。新的`powerInner`方法如下所示： ~~~ private double powerInner(double base, long exponent) { if (exponent == 0) { return 1; } else if (exponent == 1) { return base; } double result = powerInner(base, exponent >> 1); result *= result; if ((exponent & 0x1) == 1) { result *= base; } return result; } ~~~ 這里用右移運算符代替了除以2，用位于運算代替了求余運算符來判斷一個數是不是奇數。 ### 1.2 (17)打印1到最大的n位數[?](https://blog.yorek.xyz/leetcode/code_interviews_3/#12-171n "Permanent link") > 輸入數字n，按順序打印出從1最大的n位十進制數。比如輸入3，則打印出1、2、3一直到最大的3位數即999。 當輸入的n很大時，我們求最大的n位數是不是用int或者long都會溢出。也就是說我們需要考慮大數問題。我們需要使用字符串模擬數字加法的解法。 **使用字符串模擬數字加法** ~~~ private void print1ToMaxOfNDigits_1(int n) { if (n <= 0) return; char[] number = new char[n]; // 初始化字符串 for (int i = 0; i < n; i++) { number[i] = '0'; } while (!increment(number)) { printNumber(number); } } private boolean increment(char[] number) { boolean isOverflow = false; int takeOver = 0; int length = number.length; for (int i = length - 1; i >= 0; i--) { int sum = number[i] - '0' + takeOver; if (i == length - 1) { sum++; } if (sum >= 10) { // 累加有進位 if (i == 0) { // 已經打印完畢了，設置為true，不在繼續計數 isOverflow = true; } else { // 還沒有打印完畢，在后續循環中進行進位操作 sum -= 10; takeOver = 1; number[i] = (char) (sum + '0'); } } else { // 累加沒有進位，直接結束循環 number[i] = (char) ('0' + sum); break; } } return isOverflow; } // ====================公共函數==================== private void printNumber(char[] number) { boolean begin0 = true; for (char ch: number) { // 只需要略過打頭的0 if (begin0 && ch != '0') { begin0 = false; } if (!begin0) { System.out.print(ch); } } System.out.println(); } ~~~ **解法二：數字排列解法，遞歸實現** 上面的思路比較直觀，戴氏代碼有點長，在短短幾十分鐘時間內完整、正確地寫出這么長的代碼，不是一件容易的事情。 我們換一種思路考慮這個問題，如果我們在數字前面補0，就會發現n位所有十進制數其實就是n個從0到9的全排列。也就是說，我們把數字的每一位都從0到9排列一遍，就得到了所有的十進制數。只是在打印的時候，排在前面的0不打印出來罷了。 全排列用遞歸很容易實現，數字的每一位都可能是0到9中的一個數，然后設置下一位。遞歸結束的條件就是我們已經設置了數字的最后一位。 ~~~ private void print1ToMaxOfNDigits_2(int n) { if (n <= 0) return; char[] number = new char[n]; // 設置第0位 for (int i = 0; i < 10; i++) { number[0] = (char) (i + '0'); print1ToMaxOfNDigits_2_Recursively(number, n, 0); } } private void print1ToMaxOfNDigits_2_Recursively(char[] number, int length, int index) { // 已經設置了最后一位，直接打印即可 if (index == length - 1) { printNumber(number); return; } // 設置第index+1位 for (int i = 0; i < 10; i++) { number[index + 1] = (char) (i + '0'); print1ToMaxOfNDigits_2_Recursively(number, length, index + 1); } } ~~~ 相關題目 定義一個函數，在該函數中可以實現任意兩個整數的加法。 由于沒有限定輸入兩個數的大小范圍，我們也要把它當做大數問題來處理。在前面的代碼的第一種思路中，實現了在字符串表示的數字上加1的功能，我們可以參考這種思路實現兩個數字的相加功能。另外還有一個需要注意的問題：如果輸入的數字中有負數，那么我們該怎么處理？ 面試小提示 如果面試題是關于n位的整數并且沒有限定n的取值范圍，或者輸入任意大小的整數，那么這道題目很有可能是需要考慮大數問題的。字符串是一種簡單、有效地表示大數的方法。 ### 1.3 (18)刪除鏈表的節點[?](https://blog.yorek.xyz/leetcode/code_interviews_3/#13-18 "Permanent link") #### 1.3.1 在O(1)時間刪除鏈表結點[?](https://blog.yorek.xyz/leetcode/code_interviews_3/#131-o1 "Permanent link") > 給定單向鏈表的頭指針和一個結點指針，定義一個函數在O(1)時間刪除該結點。 常規的做法需要從頭開始順序查找，得到將要被刪除的節點的前一個節點。 但是，在一般情況下，我們可以很方便地得到要刪除節點的下一個節點。如果我們把下一個節點的內容復制到需要刪除的節點上覆蓋原有的內容，在把下一個節點刪除，那就相當于把當前需要刪除的節點刪除了。 這個思路有一個問題：如果要刪除的節點位于鏈表的尾部，那么它就沒有下一個節點，這時仍然需要從頭開始遍歷，得到該節點的前序節點，然后完成刪除操作。 最后需要注意的是，如果鏈表中只有一個節點，而我們又需要刪除鏈表的頭結點，那么此時我們在刪除節點后，還需要鏈表的頭結點設置為null。 總的時間復雜度是\[(n-1) \\times O(1)+O(n)\]/n，結果還是O(1)。但是這基于一個假設，要刪除的節點的確在鏈表中。 ~~~ private ListNode deleteNode(ListNode head, ListNode toBeDeleted) { if (head == null || toBeDeleted == null) { return null; } // 要刪除的結點不是尾結點 if (toBeDeleted.next != null) { toBeDeleted.value = toBeDeleted.next.value; toBeDeleted.next = toBeDeleted.next.next; } else if (head == toBeDeleted) { // 鏈表只有一個結點，刪除頭結點（也是尾結點） head = null; } else { // 鏈表中有多個結點，刪除尾結點 ListNode p = head; while (p.next != toBeDeleted) { p = p.next; } p.next = null; } return head; } ~~~ #### 1.3.2 刪除鏈表中重復的結點[?](https://blog.yorek.xyz/leetcode/code_interviews_3/#132 "Permanent link") > 在一個排序的鏈表中，如何刪除重復的結點？例如，在圖3.4（a）中重復結點被刪除之后，鏈表如圖3.4（b）所示。  刪除鏈表中重復的節點 注：(a)一個有7個節點的鏈表：1、2、3、3、4、4、5；(b)當重復的節點被刪除之后，鏈表中只剩下3個節點。 **弄一個頭結點可以有效的規避邊界問題。** ~~~ private ListNode deleteDuplication(ListNode head) { if (head == null) { return null; } // 創建一個頭結點 ListNode rHead = new ListNode(0); rHead.next = head; ListNode p, q; p = rHead; while (p.next != null) { q = p.next; boolean duplicate = false; while (q.next != null && q.value == q.next.value) { duplicate = true; q = q.next; } if (duplicate) { p.next = q.next; } else { p = q; } } return rHead.next; } ~~~ ### 1.4 (19)正則表達式匹配[?](https://blog.yorek.xyz/leetcode/code_interviews_3/#14-19 "Permanent link") > 請實現一個函數用來匹配包含‘.’和‘\*’的正則表達式。模式中的字符‘.’表示任意一個字符，而‘\*’表示它前面的字符可以出現任意次（含0次）。在本題中，匹配是指字符串的所有字符匹配整個模式。例如，字符串“aaa”與模式“a.a”和“ab\*ac\*a”匹配，但與“aa.a”及“ab\*a”均不匹配。 代碼同[LC-10-Regular Expression Matching](https://blog.yorek.xyz/leetcode/leetcode1-10/#10-regular-expression-matching)。 在輸入參數有效的情況下，先檢查模式中第二個字符是不是'\*'。 * 若不是，那么本次只需要比較字符串中第一個字符和模式中的第一個字符是否相匹配。若匹配，那么字符串和模式都向后移動一個字符，然后匹配剩余的字符串和模式。若不匹配，直接返回false。 * 若是'\*',那么有兩種匹配方式： 1. "aab"、"c\*a\*b"方式 此時在模式上向后移動兩個字符即可。 2. "aaa"、"a\*a"方式 此時如果第一個字符可以匹配，則在字符串上向后移動一個字符，模式保持不變即可。 代碼Copy如下： ~~~ class Solution { public boolean isMatch(String text, String pattern) { if (pattern.isEmpty()) return text.isEmpty(); boolean first_match = (!text.isEmpty() && (pattern.charAt(0) == text.charAt(0) || pattern.charAt(0) == '.')); if (pattern.length() >= 2 && pattern.charAt(1) == '*'){ return (isMatch(text, pattern.substring(2)) || (first_match && isMatch(text.substring(1), pattern))); } else { return first_match && isMatch(text.substring(1), pattern.substring(1)); } } } ~~~ ### 1.5 (20)表示數值的字符串[?](https://blog.yorek.xyz/leetcode/code_interviews_3/#15-20 "Permanent link") > 請實現一個函數用來判斷字符串是否表示數值（包括整數和小數）。例如，字符串“+100”、“5e2”、“-123”、“3.1416”及“-1E-16”都表示數值，但“12e”、“1a3.14”、“1.2.3”、“+-5”及“12e+5.4”都不是。 此題和[LC-65-Valid Number](https://blog.yorek.xyz/leetcode/leetcode61-70/#65-valid-number)相識 表示數值的字符串遵循模式A\[.\[B\]\]\[e|EC\]或者.B\[e|EC\]，其中A為數值的整數部分，B緊跟著小數點為數值的小數部分，C緊跟著e或者E，為數值的指數部分。在小數里可能沒有數值的整數部分。例如，小數.123等于0.123。因此A部分不是必須的。如果一個數沒有整數部分，那么它的小數部分不能為空。 上述A和C都是可能以+或者-開頭的0~9的數位串；B也是0~9的數位串，但前面不能有正負號。 以表示數值的字符串"123.45e+6"為例，"123"就是A，"45"就是B，"+6"就是C。 ~~~ private int index; private boolean isNumeric(String str) { if (str == null) { return false; } return isNumeric(str.toCharArray()); } private boolean isNumeric(char[] str) { index = 0; boolean numeric = scanInteger(str); // 如果出現'.'，接下來是數字的小數部分 if (index < str.length && str[index] == '.') { index++; // 下面一行代碼用||的原因： // 1. 小數可以沒有整數部分，例如.123等于0.123；此時原來的numeric=false // 2. 小數點后面可以沒有數字，例如233.等于233.0；此時原來的numeric=true // 3. 當然小數點前面和后面可以有數字，例如233.666；此時原來的numeric=true numeric = scanUnsignedInteger(str) || numeric; } // 如果出現'e'或者'E'，接下來跟著的是數字的指數部分 if (index < str.length && (str[index] == 'e' || str[index] == 'E')) { index++; // 下面一行代碼用&&的原因： // 1. 當e或E前面沒有數字時，整個字符串不能表示數字，例如.e1、e1；此時原來的numeric=false // 2. 當e或E后面沒有整數時，整個字符串不能表示數字，例如12e、12e+5.4；此時原來的numeric=true numeric = numeric && scanInteger(str); } return index == str.length && numeric; } private boolean scanInteger(char[] str) { if (index < str.length && (str[index] == '-' || str[index] == '+')) { index++; } return scanUnsignedInteger(str); } private boolean scanUnsignedInteger(char[] str) { int tmp = index; while (index < str.length && str[index] >= '0' && str[index] <= '9') { index++; } return index > tmp; } ~~~ ### 1.6 (21)調整數組順序使奇數位于偶數前面[?](https://blog.yorek.xyz/leetcode/code_interviews_3/#16-21 "Permanent link") > 輸入一個整數數組，實現一個函數來調整該數組中數字的順序，使得所有奇數位于數組的前半部分，所有偶數位于數組的后半部分。 **解法一：完成基本功能** 該題只要求把奇數放在數組的前半部分，偶數放在數組的后半部分，因此所有的奇數應該位于偶數的前面。所以我們可以寫出下面這段代碼。 ~~~ void reorderOddEven_1(int[] pData, int length) { if (pData == null || length == 0) { return; } int lo = 0, hi = length - 1; while (lo < hi) { // 向后移動lo，直到它指向偶數 while (lo < hi && (pData[lo] & 0x1) != 0) { lo++; } // 向前移動hi，直到它指向奇數 while (lo < hi && (pData[hi] & 0x1) == 0) { hi--; } if (lo < hi) { int temp = pData[lo]; pData[lo] = pData[hi]; pData[hi] = temp; } } } ~~~ **解法二：考慮可擴展性** 我們需要提供解決一系列同類型題目的通用方法。這只需要替換方法中兩處判斷即可。 下面這段代碼提供了一個參數并返回一個值的通用接口`Function<P1, R>`，在此接口上實現了一個`IsEvenFunction`用來解決具體問題。 ~~~ /** A function that takes 1 argument. */ private interface Function<P1, R> { R invoke(P1 n); } private void reorderOddEven_2(int[] pData, int length) { reorder(pData, length, new IsEvenFunction()); } private void reorder(int[] pData, int length, Function<Integer, Boolean> function) { if (pData == null || length == 0) { return; } int lo = 0, hi = length - 1; while (lo < hi) { // 向后移動pBegin，直到它指向偶數 while (lo < hi && !function.invoke(pData[lo])) { lo++; } // 向前移動pEnd，直到它指向奇數 while (lo < hi && function.invoke(pData[hi])) { hi--; } if (lo < hi) { int temp = pData[lo]; pData[lo] = pData[hi]; pData[hi] = temp; } } } private class IsEvenFunction implements Function<Integer, Boolean> { @Override public Boolean invoke(Integer n) { return (n & 1) == 0; } } ~~~ 在上面的代碼中，方法根據function的實現把數組分成兩部分。如果把問題改成數組中的負數移到非負數的前面，或者把能被3整除的數移到不能被3整除的數前面，都只需要定義新的函數來確定分組的標準，而方法不需要進行任何修改。也就是說，解耦的好處就是提高了代碼的重用性，為功能擴展提供了便利。 ## 2\. 代碼的魯棒性[?](https://blog.yorek.xyz/leetcode/code_interviews_3/#2 "Permanent link") 魯棒是英文*Robust*的音譯，也翻譯成健壯性。所謂魯棒性是指程序能夠判斷輸入是否合乎規范要求，并對不符合要求的輸入予以合理的處理。 容錯性是魯棒性的一個重要體現。 提高代碼的魯棒性的有效途徑是進行防御性編程。防御性編程是一種編程習慣，是指預見在什么地方可能會出現問題，并為這些可能出現的問題制定處理方式。 在面試時，最簡單也最實用的防御性編程就是在函數入口添加代碼以驗證用戶輸入是否符合要求。 當然，并不是所有與魯棒性相關的問題都只是檢查輸入的參數那么簡單。 ### 2.1 (22)鏈表中倒數第k個結點[?](https://blog.yorek.xyz/leetcode/code_interviews_3/#21-22k "Permanent link") > 輸入一個鏈表，輸出該鏈表中倒數第k個結點。為了符合大多數人的習慣，本題從1開始計數，即鏈表的尾結點是倒數第1個結點。例如一個鏈表有6個結點，從頭結點開始它們的值依次是1、2、3、4、5、6。這個鏈表的倒數第3個結點是值為4的結點。 該題同[LC-19-Remove Nth Node From End of List](https://blog.yorek.xyz/leetcode/leetcode11-20/#19-remove-nth-node-from-end-of-list) 代碼Copy如下： ~~~ private ListNode findKthToTail(ListNode pListHead, int k) { if (pListHead == null || k <= 0) { return null; } ListNode p = pListHead; int i = 1; while (i < k && p != null) { p = p.next; i++; } if (p == null) { return null; } ListNode q = pListHead; while (p.next != null) { p = p.next; q = q.next; } return q; } ~~~ 相關題目 求鏈表的中間節點。如果鏈表中的節點總數為奇數，則返回中間節點；如果節點總數是偶數，則返回中間兩個節點的任意一個。為了解決這個問題，我們也可以定義兩個指針，同時從鏈表的頭結點出發，一個指針一次走一步，另一個指針一次走兩步。當走得快的指針走到鏈表的末尾時，走得慢的指針正好在鏈表的中間。 舉一反三 當我們用一個指針遍歷鏈表不能解決問題的時候，可以嘗試用兩個指針遍歷鏈表。可以讓其中一個指針遍歷的速度快一些（比如一次在鏈表上走兩步），或者讓它先在鏈表上走若干步。 ### 2.2 (23)鏈表中環的入口結點[?](https://blog.yorek.xyz/leetcode/code_interviews_3/#22-23 "Permanent link") > 一個鏈表中包含環，如何找出環的入口結點？例如，在圖3.8的鏈表中，環的入口結點是結點3。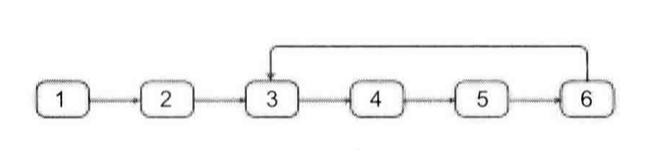  節點3是鏈表中環的入口節點 解決這個問題的第一步是如何確定一個鏈表中包含環。第二步是如何找到環的入口。 解法步驟如下： 1. 找出環中任意一個節點； 2. 得到環中節點的數目； 3. 找到環的入口節點。 ~~~ private ListNode entryNodeOfLoop(ListNode head) { ListNode meetingNode = meetingNode(head); if (meetingNode == null) { return null; } // 計算環中節點個數 int nodesInLoop = 1; ListNode node1 = meetingNode; while (node1.next != meetingNode) { nodesInLoop++; node1 = node1.next; } // 將node1從頭開始移動nodesInLoop次 node1 = head; for (int i = 0; i < nodesInLoop; i++) { node1 = node1.next; } // 將node1、node2同時移動 ListNode node2 = head; while (node1 != node2) { node1 = node1.next; node2 = node2.next; } return node1; } private ListNode meetingNode(ListNode head) { if (head == null) { return null; } ListNode slow = head.next; if (slow == null) { return null; } ListNode fast = slow.next; while (fast != null && slow != null) { if (fast == slow) { return fast; } slow = slow.next; fast = fast.next; if (fast != null) { fast = fast.next; } } return null; } ~~~ ### 2.3 (24)反轉鏈表[?](https://blog.yorek.xyz/leetcode/code_interviews_3/#23-24 "Permanent link") > 定義一個函數，輸入一個鏈表的頭結點，反轉該鏈表并輸出反轉后鏈表的頭結點。 ~~~ private ListNode reverseList(ListNode head) { if (head == null || head.next == null) { return head; } ListNode p = head, q = p.next; head.next = null; while (q != null) { p = q.next; q.next = head; head = q; q = p; } return head; } ~~~ 此題注意需要用以下幾類測試用例對代碼進行功能測試： * 輸入的鏈表頭指針是null * 輸入的鏈表只有一個節點 * 輸入的鏈表有多個節點 本題擴展 用遞歸實現同樣的反轉鏈表的功能。 ~~~ private ListNode reverseList(ListNode head) { if (head == null || head.next == null) { return head; } ListNode next = head.next; head.next = null; ListNode reversed = reverseList(next); next.next = head; return reversed; } ~~~ ### 2.4 (25)合并兩個排序的鏈表[?](https://blog.yorek.xyz/leetcode/code_interviews_3/#24-25 "Permanent link") > 輸入兩個遞增排序的鏈表，合并這兩個鏈表并使新鏈表中的結點仍然是按照遞增排序的。例如輸入圖中的鏈表1和鏈表2，則合并之后的升序鏈表如鏈表3所示。  合并兩個鏈表排序的過程 此題同[LC-21-Merge Two Sorted Lists](https://blog.yorek.xyz/leetcode/leetcode21-30/#21-merge-two-sorted-lists)。 注意操作列表最好不要直接操作入參列表，所以合并的時候會創建一些節點。 代碼Copy如下： ~~~ class Solution { public ListNode mergeTwoLists(ListNode l1, ListNode l2) { ListNode result = new ListNode(0), p = l1, q = l2, m = result; while (p != null || q != null) { if (p == null) { m.next = q; return result.next; } if (q == null) { m.next = p; return result.next; } if (p.val < q.val) { m.next = new ListNode(p.val); p = p.next; } else { m.next = new ListNode(q.val); q = q.next; } m = m.next; } return result.next; } } ~~~ ### 2.5 (26)樹的子結構[?](https://blog.yorek.xyz/leetcode/code_interviews_3/#25-26 "Permanent link") > 輸入兩棵二叉樹A和B，判斷B是不是A的子結構。 例如圖中的兩顆二叉樹，由于A中有一部分子樹的結構和B是一樣的，因此B是A的子結構。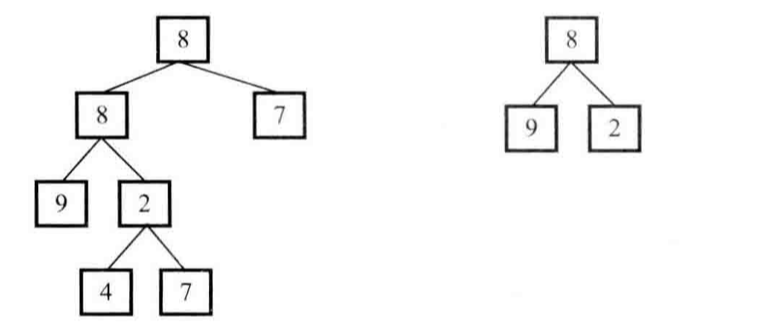  兩顆二叉樹A和B，右邊的樹B是左邊的樹A的子結構 要查找樹A中是否存在和樹B結構一樣的子樹，我們可以分為兩步： * 第一步，在樹A中找到和樹B的根節點的值一樣的節點R * 第二步，判斷樹A中以R為根節點的子樹是不是包含和樹B一樣的結構 ~~~ private boolean hasSubtree(BinaryTreeNode root1, BinaryTreeNode root2) { boolean result = false; if (root1 != null && root2 != null) { result = doesTree1HasTree2(root1, root2); if (!result) { result = hasSubtree(root1.left, root2); } if (!result) { result = hasSubtree(root1.right, root2); } } return result; } private boolean doesTree1HasTree2(BinaryTreeNode root1, BinaryTreeNode root2) { if (root2 == null) { return true; } if (root1 == null) { return false; } if (root1.value != root2.value) { return false; } return doesTree1HasTree2(root1.left, root2.left) && doesTree1HasTree2(root1.right, root2.right); } ~~~