[TOC] ## 常見API ``` //數據結構 Integer? Character //操作 contains equlas //棧 Stack? stack = new Stack push? peek(不出)? pop //隊列 Queue queue = new LinkedList<>(); queue.offer queue.peek(不出 ) queue.poll // 比較 new Comparator() { @Override public int compare(Integer o1, Integer o2) { return o2 - o1; } } //遍歷 for(Map.Entry entry : valueCountMap.entrySet()) { if (entry.getValue() > nums.length/2) { return entry.getKey; } } StringBuilder res = new StringBuilder(); res.append(s.charAt(j)); ``` ## 位運行 本文解法基于此性質：二叉搜索樹的中序遍歷為?遞增序列?。位運算只有5種運算：與、或、異或、左移、右移。與、或、異或運算的規律可以用下表總結：|?與(&)?|?0?&?0?=?0?|?1?&?0?=?0?|?0?&?1?=?0?|?1?&?1?=?1?||?或(|)?|?0?|?0?=?0?|?1?|?0?=?1?|?0?|?1?=?1?|?1?|?1?=?1?||?異或(^)?|?0?^?0?=?0?|?1?^?0?=?1?|?0?^?1?=?1?|?1?^?1?=?0?|左移運算符m<<n表示把m左移n位。在左移n位的時候，最左邊的n位會被丟棄，同時在最右邊補上n個0。比如：00001010?<<?2?=?0010100010001010?<<?3?=?01010000 ##二分算法 ### 普通二分 https://leetcode-cn.com/problems/binary-search/solution/er-fen-cha-zhao-xiang-jie-by-labuladong/ 這個場景是最簡單的，肯能也是大家最熟悉的，即搜索一個數，如果存在，返回其索引，否則返回 -1。 ``` int binarySearch(int[] nums, int target) { int left = 0; int right = nums.length - 1; // 注意 while(left <= right) { int mid = left + (right - left) / 2; if(nums[mid] == target) return mid; else if (nums[mid] < target) left = mid + 1; // 注意 else if (nums[mid] > target) right = mid - 1; // 注意 } return -1; } ``` 1、為什么 while 循環的條件中是 <=，而不是 <？ 答：因為初始化 right 的賦值是 nums.length - 1，即最后一個元素的索引，而不是 nums.length。 這二者可能出現在不同功能的二分查找中，區別是：前者相當于兩端都閉區間 [left, right]，后者相當于左閉右開區間 [left, right)，因為索引大小為 nums.length 是越界的。 我們這個算法中使用的是前者 [left, right] 兩端都閉的區間。這個區間其實就是每次進行搜索的區間。 什么時候應該停止搜索呢？當然，找到了目標值的時候可以終止： if(nums[mid] == target) return mid; 但如果沒找到，就需要 while 循環終止，然后返回 -1。那 while 循環什么時候應該終止？搜索區間為空的時候應該終止，意味著你沒得找了，就等于沒找到嘛。 while(left <= right) 的終止條件是 left == right + 1，寫成區間的形式就是 [right + 1, right]，或者帶個具體的數字進去 [3, 2]，可見這時候區間為空，因為沒有數字既大于等于 3 又小于等于 2 的吧。所以這時候 while 循環終止是正確的，直接返回 -1 即可。 while(left < right) 的終止條件是 left == right，寫成區間的形式就是 [left, right]，或者帶個具體的數字進去 [2, 2]，這時候區間非空，還有一個數 2，但此時 while 循環終止了。也就是說這區間 [2, 2] 被漏掉了，索引 2 沒有被搜索，如果這時候直接返回 -1 就是錯誤的。 當然，如果你非要用 while(left < right) 也可以，我們已經知道了出錯的原因，就打個補丁好了： //... while(left < right) { // ... } return nums[left] == target ? left : -1; 2、為什么 left = mid + 1，right = mid - 1？我看有的代碼是 right = mid 或者 left = mid，沒有這些加加減減，到底怎么回事，怎么判斷？ 答：這也是二分查找的一個難點，不過只要你能理解前面的內容，就能夠很容易判斷。 剛才明確了「搜索區間」這個概念，而且本算法的搜索區間是兩端都閉的，即 [left, right]。那么當我們發現索引 mid 不是要找的 target 時，下一步應該去搜索哪里呢？ 當然是去搜索 [left, mid-1] 或者 [mid+1, right] 對不對？因為 mid 已經搜索過，應該從搜索區間中去除。 ### 求邊界二分 https://leetcode-cn.com/problems/find-first-and-last-position-of-element-in-sorted-array/solution/zhe-shi-er-fen-zui-zui-zui-jing-dian-de-xlvf3/ **求左邊界：向下取整，等號歸右，左加一 求右邊界：向上取整，等號歸左，右減一** * 求左邊界 ``` int left = 0, right = n-1; while(left < right){//求左邊界(注意這里不要等號) int mid = (left+right)>>1;//向下取整 if(nums[mid] >= target) right = mid;//等號歸右 else left = mid+1;//左加一 } //此時right即為所求 ``` * 求右邊界 ``` int left = 0, right = n-1; while(left<right){//求右邊界(注意這里不要等號) int mid = (left + right +1)>>1;//向上取整 if(nums[mid] <= target) left = mid;//等號歸左 else right = mid-1;//右減一 } //此時right即為所求 ``` ### 循環數組 [劍指 Offer 11. 旋轉數組的最小數字](https://leetcode-cn.com/problems/xuan-zhuan-shu-zu-de-zui-xiao-shu-zi-lcof/) ## 單例模式 ~~~ public class Singleton { private volatile static Singleton singleton; private Singleton (){} public static Singleton getSingleton() { if (singleton == null) { synchronized (Singleton.class) { if (singleton == null) { singleton = new Singleton(); } } } return singleton; } } ~~~ ## 生產者消費者模型 生產者生產數據到緩沖區中，消費者從緩沖區中取數據。 如果緩沖區已經滿了，則生產者線程阻塞； 如果緩沖區為空，那么消費者線程阻塞。 ~~~ public interface ITaskQueue{ public void add(); public int remove(); } public class Consumer extends Thread{ ITaskQueue queue; public Consumer(ITaskQueue queue){ this.queue = queue; } public void run(){ while(true){ try { Thread.sleep((long) (1000 * Math.random())); } catch (InterruptedException e) { e.printStackTrace(); } queue.remove(); } } } public class Producer extends Thread{ ITaskQueue queue; public Producer(ITaskQueue queue){ this.queue = queue; } public void run(){ while(true){ try { Thread.sleep((long) (1000 * Math.random())); } catch (InterruptedException e) { e.printStackTrace(); } queue.add(); } } ~~~ ### 使用synchronized wait notify ~~~ public void TaskQueue1 implements ITaskQueue{ //當前資源數量 private int num = 0; //資源池中允許存放的資源數目 private int size = 10; public synchronized void add(){ if(num >= size){ wait(); }else{ num ++; notifyAll(); } } public synchronized void remove(){ if(num <= 0){ wait(); }else{ num --; notifyAll(); } } } ~~~ ### 使用BlockingQueue ~~~ public void TaskQueue2 implements ITaskQueue{ private ArrayBlockingQueue<Integer> queue = new ArrayBlockingQueue<>(); public void add(){ queue.put(1); } public void remove(){ queue.talke(); } } ~~~ ## 排序 https://leetcode-cn.com/problems/sort-an-array/  ### 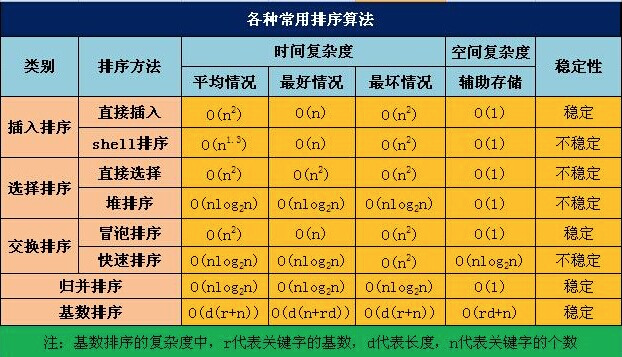快排 1. 從數列中挑出一個元素，稱為 “基準”（pivot）； 2. 重新排序數列，所有元素比基準值小的擺放在基準前面，所有元素比基準值大的擺在基準的后面（相同的數可以到任一邊）。在這個分區退出之后，該基準就處于數列的中間位置。這個稱為分區（partition）操作； 3. 遞歸地（recursive）把小于基準值元素的子數列和大于基準值元素的子數列排序。 ``` public class QuickSort { public static void quickSort(int[] arr,int low,int high){ int i,j,temp,t; if(low>high){ return; } i=low; j=high; //temp就是基準位 temp = arr[low]; while (i<j) { //先看右邊，依次往左遞減 while (temp<=arr[j]&&i<j) { j--; } //再看左邊，依次往右遞增 while (temp>=arr[i]&&i<j) { i++; } //如果滿足條件則交換 if (i<j) { t = arr[j]; arr[j] = arr[i]; arr[i] = t; } } //最后將基準為與i和j相等位置的數字交換 arr[low] = arr[i]; arr[i] = temp; //遞歸調用左半數組 quickSort(arr, low, j-1); //遞歸調用右半數組 quickSort(arr, j+1, high); } public static void main(String[] args){ int[] arr = {10,7,2,4,7,62,3,4,2,1,8,9,19}; quickSort(arr, 0, arr.length-1); for (int i = 0; i < arr.length; i++) { System.out.println(arr[i]); } } } ``` ### 歸并 1. 把長度為n的輸入序列分成兩個長度為n/2的子序列； 2. 對這兩個子序列分別采用歸并排序； 3. 將兩個排序好的子序列合并成一個最終的排序序列。  ### 大頂堆 ## 二叉樹 [二叉樹的后序遍歷(遞歸與非遞歸實現)](https://blog.csdn.net/LK274857347/article/details/77678464) ### 深度優先的遍歷（棧） #### 先序遍歷 https://leetcode-cn.com/problems/binary-tree-preorder-traversal/ #### 中序遍歷 https://leetcode-cn.com/problems/binary-tree-inorder-traversal/ #### 后序遍歷 https://segmentfault.com/a/1190000016674584 好理解，雙堆棧法 1. 用一個棧實現`根->右->左`的遍歷 2. 用另一個棧將遍歷順序反過來，使之變成`左->右->根` ``` class Solution { public List<Integer> postorderTraversal(TreeNode root) { List<Integer> result = new LinkedList<>(); if (root == null) return result; Stack<TreeNode> toVisit = new Stack<>(); Stack<TreeNode> reversedStack = new Stack<>(); toVisit.push(root); TreeNode cur; while (!toVisit.isEmpty()) { cur = toVisit.pop(); reversedStack.push(cur); // result.add(cur.val); if (cur.left != null) toVisit.push(cur.left); // 左節點入棧 if (cur.right != null) toVisit.push(cur.right); // 右節點入棧 } while (!reversedStack.isEmpty()) { cur = reversedStack.pop(); result.add(cur.val); } return result; } } ``` #### 層次遍歷 ### 廣度優先的遍歷（隊列）