[TOC] ## 1\. (53)在排序數組中查找數字[?](https://blog.yorek.xyz/leetcode/code_interviews_6/#1-53 "Permanent link") ### 1.1 數字在排序數組中出現的次數[?](https://blog.yorek.xyz/leetcode/code_interviews_6/#11 "Permanent link") > 統計一個數字在排序數組中出現的次數。例如輸入排序數組{1, 2, 3, 3, 3, 3, 4, 5}和數字3，由于3在這個數組中出現了4次，因此輸出4。 利用二分查找分別查找第一個k和最后一個k。它們的時間復雜度都是O(logn)，因此總的時間復雜度也只有O(longn)。 ~~~ private int getNumberOfK(int[] data, int k) { if (data == null || data.length == 0) return 0; int firstK = getFirstK(data, k, 0, data.length - 1); int lastK = getLastK(data, k, 0, data.length - 1); if (firstK > -1 && lastK > -1) return lastK - firstK + 1; return 0; } private int getFirstK(int[] data, int k, int start, int end) { if (start > end) { return -1; } int middle = (start + end) >> 1; if (data[middle] == k) { if (middle == 0 || data[middle - 1] != k) { return middle; } else { end = middle - 1; } } else if (data[middle] < k) { start = middle + 1; } else { end = middle - 1; } return getFirstK(data, k, start, end); } private int getLastK(int[] data, int k, int start, int end) { if (start > end) { return -1; } int middle = (start + end) >> 1; if (data[middle] == k) { if (middle == data.length - 1 || data[middle + 1] != k) { return middle; } else { start = middle + 1; } } else if (data[middle] < k) { start = middle + 1; } else { end = middle - 1; } return getLastK(data, k, start, end); } ~~~ ### 1.2 0到n-1中缺失的數字[?](https://blog.yorek.xyz/leetcode/code_interviews_6/#12-0n-1 "Permanent link") > 一個長度為n-1的遞增排序數組中的所有數字都是唯一的，并且每個數字都在范圍0到n-1之內。在范圍0到n-1的n個數字中有且只有一個數字不在該數組中，請找出這個數字。 這個問題有一個直觀的解決方案。我們可以先用公式n(n-1)/2求出數字0~n-1的所有數字之和，記為s\_1。接著求出數組中所有數字的和，記為s\_2。那個不在數組中的數字就是s\_1-s\_2的差。這種解法需要O(n)的時間求數組中所有數字的和。顯然，該解法沒有有效利用數組是遞增排序的這一特點。 因為0~n-1這些數字在數組中是排序的，因此數組中開始的一些數字與它們的下標相同。也就是說，0在下標為0的位置，1在下標為1的位置，以此類推。如果不在數組中的那個數字記為m，那么所有比m小的數字的下標都與它們的值相同。 由于m不在數組中，那么m+1處在下標為m的位置，m+2處在下標為m+1的位置，以此類推。**我們發現m正好是數組中第一個數值和下標不相等的下標，因此這個問題轉換成在排序數組中找出第一個值和下標不相等的元素**。 我們可以基于二分查找的算法用如下過程查找：如果中間元素的值和下標相等，那么下一輪查找只需要查找右半邊；如果中間元素的值和下標不相等，并且它前面一個元素和它的下標相等，這意味著這個中間的數字正好是第一個值和下標不相等的元素，它的下標就是在數組中不存在的數字；如果中間元素的值和下標不相等，并且它前面一個元素和它的下標不相等，這意味著下一輪查找我們只需要在左半邊查找即可。 ~~~ private int getMissingNumber(int[] data) { if (data == null || data.length == 0) return -1; final int n = data.length; int start = 0; int end = n - 1; int middle; while (end >= start) { middle = (start + end) >> 1; if (data[middle] != middle) { if (middle == 0 || data[middle - 1] == middle - 1) { return middle; } end = middle - 1; } else { start = middle + 1; } } if (start == n) { return n; } // 無效的輸入，比如數組不是按要求排序的， // 或者有數字不在0到n-1范圍之內 return -1; } ~~~ ### 1.3 數組中數值和下標相等的元素[?](https://blog.yorek.xyz/leetcode/code_interviews_6/#13 "Permanent link") > 假設一個單調遞增的數組里的每個元素都是整數并且是唯一的。請編程實現一個函數找出數組中任意一個數值等于其下標的元素。例如，在數組{-3, -1, 1, 3, 5}中，數字3和它的下標相等。 我們很容易就能想到最直觀的解法：從頭到尾依次掃描數組中的數字，并逐一檢驗數字是不是和下標相等。顯然，這種算法的時間復雜度是O(n)由于數組是單調遞增排序的，因此我們可以嘗試用二分查找算法來進行優化。假設我們某一步抵達數組中的第i個數字。如果我們很幸運，該數字的值剛好也是i，那么我們就找到了一個數字和其下標相等。 那么當數字的值和下標不相等的時候該怎么辦呢？假設數字的值為m。我們先考慮m大于i的情形，即數字的值大于它的下標。由于數組中的所有數字都唯一并且單調遞增，那么對于任意大于0的k，位于下標i+k的數字的值大于或等于m+k。另外，因為m>i，所以m+k>i+k因此，位于下標i+k的數字的值一定大于它的下標。這意味著如果第i個數字的值大于i，那么它右邊的數字都大于對應的下標，我們都可以忽略。下一輪查找我們只需要從它左邊的數字中查找即可。 數字的值m小于它的下標i的情形和上面類似。它左邊的所有數字的值都小于對應的下標，我們也可以忽略 由于我們在每一步查找時都可以把查找的范圍縮小一半，這是典型的二分查找的過程。下面是基于二分查找的參考代碼: ~~~ private int getNumberSameAsIndex(int[] data) { if (data == null || data.length == 0) return -1; final int n = data.length; int start = 0; int end = n - 1; int middle; while (end >= start) { middle = (start + end) >> 1; if (data[middle] == middle) { return middle; } else if (data[middle] > middle) { end = middle - 1; } else { start = middle + 1; } } return -1; } ~~~ ## 2\. (54)二叉搜索樹的第k個結點[?](https://blog.yorek.xyz/leetcode/code_interviews_6/#2-54k "Permanent link") > 給定一棵二叉搜索樹，請找出其中的第k大的結點。例如，在圖中的二叉搜索樹里，按節點數值大小順序，第三大節點的值是4。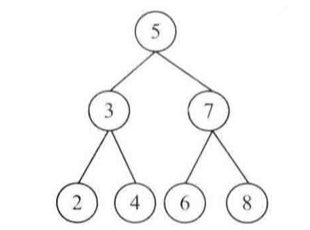  第三大節點是4 本題就是考察二叉樹的中序遍歷算法。 ~~~ private int index; private BinaryTreeNode kthNode(BinaryTreeNode root, int k) { if (root == null || k == 0) { return null; } index = 0; return kthNodeCore(root, k); } private BinaryTreeNode kthNodeCore(BinaryTreeNode root, int k) { BinaryTreeNode result = null; if (root.left != null) result = kthNodeCore(root.left, k); if (result == null) { index++; if (index == k) { result = root; } } if (result == null && root.right != null) { result = kthNodeCore(root.right, k); } return result; } ~~~ ## 3\. (55)二叉樹的深度[?](https://blog.yorek.xyz/leetcode/code_interviews_6/#3-55 "Permanent link") ### 3.1 二叉樹的深度[?](https://blog.yorek.xyz/leetcode/code_interviews_6/#31 "Permanent link") > 輸入一棵二叉樹的根結點，求該樹的深度。從根結點到葉結點依次經過的結點（含根、葉結點）形成樹的一條路徑，最長路徑的長度為樹的深度。 此題同[LC-104-Maximum Depth of Binary Tree](https://blog.yorek.xyz/leetcode/leetcode101-110/#104-maximum-depth-of-binary-tree) 我們還可以從另外一個角度來理解樹的深度。如果一棵樹只有一個節點，那么它的深度為1。如果根節點只有左子樹而沒有右子樹，那么樹的深度應該是其左子樹的深度加1；同樣，如果根節點只有右子樹而沒有左子樹，那么樹的深度應該是其右子樹的深度加1。如果既有右子樹又有左子樹，那么該樹的深度就是其左、右子樹深度的較大值再加1。 ~~~ private int treeDepth(BinaryTreeNode root) { if (root == null) { return 0; } int left = treeDepth(root.left); int right = treeDepth(root.right); return Math.max(left, right) + 1; } ~~~ ### 3.2 平衡二叉樹[?](https://blog.yorek.xyz/leetcode/code_interviews_6/#32 "Permanent link") > 輸入一棵二叉樹的根結點，判斷該樹是不是平衡二叉樹。如果某二叉樹中任意結點的左右子樹的深度相差不超過1，那么它就是一棵平衡二叉樹。 此題同[LC-110-Balanced Binary Tree](https://blog.yorek.xyz/leetcode/leetcode101-110/#110-balanced-binary-tree) **簡單解法** 有了求二叉樹的深度的經驗之后再解決這個問題，我們很容易就能想到一種思路:在遍歷樹的每個節點的時候，調用函數`treeDepth`得到它的左、右子樹的深度。如果每個節點的左、右子樹的深度相差都不超過1，那么按照定義它就是一棵平衡二叉樹。這種思路對應的代碼如下: ~~~ private boolean isBalanced1(BinaryTreeNode root) { if (root == null) { return true; } int left = treeDepth(root.left); int right = treeDepth(root.right); if (Math.abs(left - right) > 1) { return false; } return isBalanced1(root.left) && isBalanced1(root.right); } private int treeDepth(BinaryTreeNode root) { if (root == null) { return 0; } int left = treeDepth(root.left); int right = treeDepth(root.right); return Math.max(left, right) + 1; } ~~~ 上面的代碼固然簡潔，但我們也要注意到由于一個節點會被重復遍歷多次，這種思路的時間效率不高。毫無疑問，重復遍歷同一個節點會影響性能。接下來我們尋找不需要重復遍歷的算法。 **每個節點只遍歷一次** 如果我們用后序遍歷的方式遍歷二叉樹的每個節點，那么在遍歷到一個節點之前我們就已經遍歷了它的左、右子樹。只要在遍歷每個節點的時候記錄它的深度（某一節點的深度等于它到葉節點的路徑的長度），我們就可以一邊遍歷一邊判斷每個節點是不是平衡的。下面是這種思路的參考代碼: ~~~ private boolean isBalanced2(BinaryTreeNode root) { if (root == null) { return true; } return isBalanced2Core(root) >= 0; } /** * 返回值大于等于0表示是平衡的 否則不平衡 */ private int isBalanced2Core(BinaryTreeNode root) { if (root == null) { return 0; } int left = isBalanced2Core(root.left); int right = isBalanced2Core(root.right); if (left >= 0 && right >= 0) { int diff = Math.abs(left - right); if (diff <= 1) { return Math.max(left, right) + 1; } } return -1; } ~~~ ## 4\. (56)數組中數字出現的次數[?](https://blog.yorek.xyz/leetcode/code_interviews_6/#4-56 "Permanent link") ### 4.1 數組中只出現一次的兩個數字[?](https://blog.yorek.xyz/leetcode/code_interviews_6/#41 "Permanent link") > 一個整型數組里除了兩個數字之外，其他的數字都出現了兩次。請寫程序找出這兩個只出現一次的數字。要求時間復雜度是O(n)，空間復雜度是O(1)。 我們可以先考慮這個數組中只有一個數字出現了一次，其他數字出現了兩次，怎么找出這個數字？ 這兩道題目都在強調一個（或兩個）數字只出現一次，其他數字出現兩次。這有什么意義呢？**我們想到異或運算的一個性質：任何一個數字異或它自己都等于0**。 也就是說，如果我們從頭到尾依次異或數組中的每個數字，那么最終的結果剛好是那個只出現一次的數字，因為那些成對出現兩次的數字全部在異或中抵消了。 想明白怎么解決這個簡單的問題之后，我們再回到原始的問題，看看能不能運用相同的思路。我們試著把原數組分成兩個子數組，使得每個子數組包含一個只出現一次的數字，而其他數字都成對出現兩次。如果能夠這樣拆分成兩個數組，那么我們就可以按照前面的辦法分別找出兩個只出現一次的數字了。 我們還是從頭到尾依次異或數組中的每個數字，那么最終得到的結果就是兩個只出現一次的數字的異或結果，因為其他數字都出現了兩次，在異或中全部抵消了。由于這兩個數字肯定不一樣，那么異或的結果肯定不為0，也就是說，在這個結果數字的二進制表示中至少有一位為1。我們在結果數字中找到第一個為1的位的位置，記為第n位。現在我們以第n位是不是1為標準把原數組中的數字分成兩個子數組，第一個子數組中每個數字的第n位都是1，而第二個子數組中每個數字的第n位都是0。由于我們分組的標準是數字中的某一位是1還是0，那么出現了兩次的數字肯定被分配到同一個子數組。因為兩個相同的數字的任意一位都是相同的，我們不可能把兩個相同的數字分配到兩個子數組中去，于是我們已經把原數組分成了兩個子數組，每個子數組都包含一個只出現一次的數字，而其他數字都出現了兩次。我們已經知道如何在數組中找出唯一一個只出現一次的數字，因此，到此為止所有的問題都已經解決了。 舉個例子，假設輸入數組{2, 4, 3, 6, 3, 2, 5, 5}。當我們依次對數組中的每個數字進行異或運算之后，得到的結果用二進制表示是0010。異或得到的結果中的倒數第二位是1，于是我們根據數字的倒數第二位是不是1將該數組分為兩個子數組。第一個子數組{2, 3, 6, 3, 2}中所有數字的倒數第二位都是1，而第二個子數組{4, 5, 5}中所有數字的倒數第二位都是0。接下來只要分別對這兩個子數組求異或，就能找出第一個子數組中只出現一次的數字是6，而第二個子數組中只出現一次的數字是4。 ~~~ private Pair<Integer, Integer> findNumsAppearOnce(int[] data) { if (data == null || data.length == 0) return new Pair<>(-1, -1); int xor = 0; for (int num : data) { xor ^= num; } // 找到xor從右邊數起第一個是1的位 int index = 0; while ((xor & 1) == 0) { xor >>= 1; index++; } xor = 0; int xor2 = 0; for (int num : data) { if (isBit1(num, index)) { xor ^= num; } else { xor2 ^= num; } } return new Pair<>(xor, xor2); } // 判斷數字num的第index位是不是1 private boolean isBit1(int num, int index) { num >>= index; return (num & 1) == 1; } ~~~ ### 4.2 數組中唯一只出現一次的數字[?](https://blog.yorek.xyz/leetcode/code_interviews_6/#42 "Permanent link") > 在一個數組中除了一個數字只出現一次之外，其他數字都出現了三次。請找出那個只出現一次的數字。 如果我們把題目稍微改一改，那么就會容易很多：如果數組中的數字除一個只出現一次之外，其他數字都出現了兩次。我們可以用XOR異或位運算解決這個簡化的問題。由于兩個相同的數字的異或結果是0，我們把數組中所有數字異或的結果就是那個唯一只出現一次的數字。 可惜這種思路不能解決這里的問題，因為三個相同的數字的異或結果還是該數字。盡管我們這里不能應用異或運算，我們還是可以沿用位運算的思路。如果一個數字出現三次，那么它的二進制表示的每一位（0或者1）也出現三次。如果把所有出現三次的數字的二進制表示的每一位都分別加起來，那么每一位的和都能被3整除。 我們把數組中所有數字的二進制表示的每一位都加起來。如果某一位的和能被3整除，那么那個只出現一次的數字二進制表示中對應的那一位是0；否則就是1。 ~~~ private int findNumsAppearOnce(int[] data) { if (data == null || data.length == 0) { return -1; } int[] bits = new int[32]; for (int i = 0; i < data.length; i++) { int bitMask = 1; for (int j = 31; j >= 0; j--) { int bit = data[i] & bitMask; if (bit != 0) bits[j] += 1; bitMask <<= 1; } } int result = 0; for (int i = 0; i < 32; i++) { result <<= 1; result += bits[i] % 3; } return result; } ~~~ 這種解法的時間效率是O(n)。我們需要一個長度為32的輔助數組存儲二進制表示的每一位的和。由于數組的長度是固定的，因此空間效率是O(1)。該解法比其他兩種直觀的解法效率都要高: * 我們很容易就能從**排序**的數組中找到只出現一次的數字，但排序需要O(nlogn)時間； * 我們也可以用一個**哈希表**來記錄數組中每個數字出現的次數，但這個哈希表需要O(n)的空間。 ## 5\. (57)和為s的數字[?](https://blog.yorek.xyz/leetcode/code_interviews_6/#5-57s "Permanent link") ### 5.1 和為s的兩個數字[?](https://blog.yorek.xyz/leetcode/code_interviews_6/#51-s "Permanent link") > 輸入一個遞增排序的數組和一個數字s，在數組中查找兩個數，使得它們的和正好是s。如果有多對數字的和等于s，輸出任意一對即可。 我們先在數組中選擇兩個數字，如果它們的和等于輸入的s，那么我們就找到了要找的兩個數字。如果和小于s呢？我們希望兩個數字的和再大一點。由于數組已經排好序了，我們可以考慮選擇較小的數字后面的數字。因為排在后面的數字要大一些，那么兩個數字的和也要大一些，就有可能等于輸入的數字s了。同樣，當兩個數字的和大于輸入的數字的時候，我們可以選擇較大數字前面的數字，因為排在數組前面的數字要小一些。 ~~~ private Pair<Integer, Integer> findNumbersWithSum(int[] data, int sum) { if (data == null || data.length == 0) { return null; } final int n = data.length; int left = 0; int right = n - 1; while (right > left) { int tmpSum = data[left] + data[right]; if (tmpSum == sum) { return new Pair<>(data[left], data[right]); } else if (tmpSum > sum) { right--; } else { left++; } } return null; } ~~~ 該算法的時間復雜度是O(n)。 ### 5.2 為s的連續正數序列[?](https://blog.yorek.xyz/leetcode/code_interviews_6/#52-s "Permanent link") > 輸入一個正數s，打印出所有和為s的連續正數序列（至少含有兩個數）。例如輸入15，由于1+2+3+4+5=4+5+6=7+8=15，所以結果打印出3個連續序列1～5、4～6和7～8。 有了解決前面問題的經驗，我們也考慮用兩個數small和big分別表示序列的最小值和最大值。首先把small初始化為1，big初始化為2。如果從small到big的序列的和大于s，則可以從序列中去掉較小的值，也就是增大small的值。如果從small到big的序列的和小于s，則可以增大big，讓這個序列包含更多的數字。因為這個序列至少要有兩個數字，我們一直增加small到(1+s)/2為止。 ~~~ private void FindContinuousSequence(int sum) { if (sum < 3) return; int small = 1; int big = 2; int middle = (sum + 1) >> 1; int curSum = small + big; while (small < middle) { if (curSum == sum) { printResult(small, big); } while (curSum > sum && small < middle) { curSum -= small; small++; if (curSum == sum) { printResult(small, big); } } big++; curSum += big; } } private void printResult(int from, int to) { for (int i = from; i <= to; i++) System.out.printf("%d ", i); System.out.println(); } ~~~ 在上述代碼中，求連續序列的和應用了一個小技巧。通常我們可以用循環求一個連續序列的和，但考慮到每次操作之后的序列和操作之前的序列相比大部分數字都是一樣的，只是增加或者減少了一個數字，因此我們可以在前一個序列的和的基礎上求操作之后的序列的和。這樣可以減少很多不必要的運算，從而提高代碼的效率。 ## 6\. (58)翻轉字符串[?](https://blog.yorek.xyz/leetcode/code_interviews_6/#6-58 "Permanent link") ### 6.1 翻轉單詞順序[?](https://blog.yorek.xyz/leetcode/code_interviews_6/#61 "Permanent link") > 輸入一個英文句子，翻轉句子中單詞的順序，但單詞內字符的順序不變。為簡單起見，標點符號和普通字母一樣處理。例如輸入字符串"I am a student. "，則輸出"student. a am I"。 翻轉兩次字符串即可，第一次翻轉整個句子，第二次翻轉句子中的每個單詞。 ~~~ private String reverseSentence(String data) { if (data == null || data.length() == 0) { return data; } final int n = data.length(); char[] reversed = data.toCharArray(); reverse(reversed, 0, n - 1); int begin = 0, end = 0; while (begin < n) { if (reversed[begin] == ' ') { begin++; end++; } else if (end == n || reversed[end] == ' ') { reverse(reversed, begin, end - 1); begin = end++; } else { end++; } } return new String(reversed); } private void reverse(char[] data, int start, int end) { if (data == null || data.length == 0) return; while (end > start) { char tmp = data[end]; data[end] = data[start]; data[start] = tmp; start++; end--; } } ~~~ ### 6.2 左旋轉字符串[?](https://blog.yorek.xyz/leetcode/code_interviews_6/#62 "Permanent link") > 字符串的左旋轉操作是把字符串前面的若干個字符轉移到字符串的尾部。請定義一個函數實現字符串左旋轉操作的功能。比如輸入字符串"abcdefg"和數字2，該函數將返回左旋轉2位得到的結果"cdefgab"。 我們可以先把前面n個數翻轉，再翻轉其余的數，最后翻轉整個字符串即可。 比如拿"abcdefg"和數字2為例： ab cdefg -> ba gfedc -> cdefg ab ~~~ private String leftRotateString(String data, int num) { if (data == null || data.length() == 0 || data.length() < num) { return data; } final int n = data.length(); char[] result = data.toCharArray(); // 翻轉字符串的前面n個字符 reverse(result, 0, num - 1); // 翻轉字符串的后面部分 reverse(result, num, n - 1); // 翻轉整個字符串 reverse(result, 0, n - 1); return new String(result); } private void reverse(char[] data, int start, int end) { if (data == null || data.length == 0) return; while (end > start) { char tmp = data[end]; data[end] = data[start]; data[start] = tmp; start++; end--; } } ~~~ ## 7\. (59)隊列的最大值[?](https://blog.yorek.xyz/leetcode/code_interviews_6/#7-59 "Permanent link") ### 7.1 滑動窗口的最大值[?](https://blog.yorek.xyz/leetcode/code_interviews_6/#71 "Permanent link") > 給定一個數組和滑動窗口的大小，請找出所有滑動窗口里的最大值。例如，如果輸入數組{2, 3, 4, 2, 6, 2, 5, 1}及滑動窗口的大小3，那么一共存在6個滑動窗口，它們的最大值分別為{4, 4, 6, 6, 6, 5}。 對于長度為n的數組，滑動窗口大小為k的輸入來說，蠻力法的時間復雜度為O(nk)。所以不推薦。 在下面代碼中，deque是一個兩端開口的隊列，用來保存有可能是滑動窗口最大值的數字的下標。在存入一個數字的下標之前，首先要判斷隊列里已有數字是否小于待存入的數字。如果已有的數字小于待存入的數字，那么這些數字已經不可能是滑動窗口的最大值，因此它們將會被依次從隊列的尾部刪除。同時，如果隊列頭部的數字已經從窗口里滑出，那么滑出的數字也需要從隊列的頭部刪除由于隊列的頭部和尾部都有可能刪除數字，這也是需要兩端開口的隊列的原因。 這種方法的時間復雜是O(n)。 ~~~ private int[] maxInWindows(int[] num, int size) { if (num == null || num.length == 0 || size <= 0 || num.length < size) { return null; } int resultLength = num.length - size + 1; int[] result = new int[resultLength]; int index = 0; Deque<Integer> deque = new ArrayDeque<>(); for (int i = 0; i < size; i++) { while (!deque.isEmpty() && num[i] >= num[deque.peekLast()]) deque.pollLast(); deque.offer(i); } for (int i = size; i < num.length; i++) { result[index++] = num[deque.peek()]; while (!deque.isEmpty() && num[i] >= num[deque.peekLast()]) deque.pollLast(); while (!deque.isEmpty() && deque.peek() <= (i - size)) deque.poll(); deque.offer(i); } result[index++] = num[deque.peek()]; return result; } ~~~ ### 7.2 隊列的最大值[?](https://blog.yorek.xyz/leetcode/code_interviews_6/#72 "Permanent link") > 請定義一個隊列并實現函數max得到隊列里的最大值，要求函數max、push\_back和pop\_front的時間復雜度都是O(1) 如前所述，滑動窗口可以看成一個隊列，因此上題的解法可以用來實現帶max函數的隊列。 ~~~ private class InternalData { int number; int index; InternalData(int number, int index) { this.number = number; this.index = index; } } private Deque<InternalData> max = new ArrayDeque<>(); private Deque<InternalData> data = new ArrayDeque<>(); private int currentIndex; private void push_back(int number) { while (!max.isEmpty() && number >= max.peekLast().number) max.pollLast(); InternalData internalData = new InternalData(number, currentIndex); data.offer(internalData); max.offer(internalData); currentIndex++; } private int pop_front() { if (max.isEmpty()) { throw new IllegalStateException("queue is empty"); } if (max.peek().index == data.peek().index) max.poll(); return data.poll().number; } private int max() { if (max.isEmpty()) { throw new IllegalStateException("queue is empty"); } return max.peek().number; } ~~~ ## 8\. (60)n個骰子的點數[?](https://blog.yorek.xyz/leetcode/code_interviews_6/#8-60n "Permanent link") > 把n個骰子扔在地上，所有骰子朝上一面的點數之和為s。輸入n，打印出s的所有可能的值出現的概率。 骰子一共有6個面，每個面上都有一個點數，對應的是1~6之間的一個數字。所以n個骰子的點數和的最小值為n，最大值為6n。另外，根據排列組合的知識，我們還知道n個骰子的所有點數的排列數為6^n。要解決這個問題，我們需要先統計出每個點數出現的次數，然后把每個點數出現的次數除以6^n，就能求出每個點數出現的概率。 **解法一：基于遞歸求骰子點數，時間效率不夠高** 現在我們考慮如何統計每個點數出現的次數。要想求出n個骰子的點數和，可以先把n個骰子分為兩堆：第一堆只有一個；另一堆有n-1個。單獨的那一個有可能出現1~6的點數。我們需要計算1~6的每一種點數和剩下的n-1個骰子來計算點數和。接下來把剩下的n-1個骰子仍然分成兩堆:第一堆只有一個；第二堆有n-2個。我們把上一輪那個單獨骰子的點數和這一輪單獨骰子的點數相加，再和剩下的n-2個骰子來計算點數和。分析到這里，我們不難發現這是一種遞歸的思路，遞歸結束的條件就是最后只剩下一個骰子。 我們可以定義一個長度為6n-n+1的數組，將和為s的點數出現的次數保存到數組的第s-n個元素里。基于這種思路，我們可以寫出如下代碼: ~~~ final int MAX_VALUE = 6; private void printProbability1(int n) { if (n < 1) return; int[] probabilities = new int[n * MAX_VALUE - n + 1]; probability(n, probabilities); int total = (int) Math.pow(MAX_VALUE, n); for (int i = n; i <= n * MAX_VALUE; i++) { System.out.printf("%d: %d/%d\n", i, probabilities[i - n], total); } } private void probability(int n, int[] probabilities) { for (int i = 1; i <= MAX_VALUE; i++) { probability(n, n, i, probabilities); } } private void probability(int original, int current, int sum, int[] probabilities) { if (current == 1) { probabilities[sum - original]++; } else { for (int i = 1; i <= MAX_VALUE; i++) { probability(original, current - 1, i + sum, probabilities); } } } ~~~ 上面的思路很簡潔，實現起來也容易。但是基于遞歸的實現，它有很多計算是重復的，從而導致當number變大時性能慢得讓人不能接受。 **基于循環求骰子點數，時間性能好** 可以換一種思路來解決這個問題。我們可以考慮用兩個數組來存儲骰子點數的每個總數出現的次數。在一輪循環中，第一個數組中的第n個數字表示骰子和為n出現的次數。在下一輪循環中，我們加上一個新的骰子，此時和為n的骰子出現的次數應該等于上一輪循環中骰子點數和為n-1、n-2、n-3、n-4、n-5與n-6的次數的總和，所以我們把另一個數組的第n個數字設為前一個數組對應的第n-1、n-2、n-3、n-4、n-5與n-6個數字之和。基于這種思路，我們可以寫出如下代碼: ~~~ private void printProbability2(int n) { if (n < 1) return; int[][] probabilities = new int[2][n * MAX_VALUE + 1]; int flag = 0; for (int i = 1; i <= MAX_VALUE; i++) probabilities[flag][i] = 1; for (int k = 2; k <= n; k++) { for (int i = 0; i < k; i++) probabilities[1 - flag][i] = 0; for (int i = k; i <= MAX_VALUE * k; i++) { probabilities[1 - flag][i] = 0; for (int j = 1; j <= i && j <= MAX_VALUE; j++) probabilities[1 - flag][i] += probabilities[flag][i - j]; } flag = 1 - flag; } int total = (int) Math.pow(MAX_VALUE, n); for (int i = n; i <= MAX_VALUE * n; i++) { System.out.printf("%d: %d/%d\n", i, probabilities[flag][i], total); } } ~~~ 在上述代碼中，我們定義了兩個數組probabilities\[0\]和probabilities\[1\]來存儲骰子的點數之和。在一輪循環中，一個數組的第n項等于另一個數組的第n-1、n-2、n-3、n-4、n-5及n-6項的和。在下一輪循環中，我們交換這兩個數組（通過改變變量flag實現）再重復這一計算過程。 ## 9\. (61)撲克牌的順子[?](https://blog.yorek.xyz/leetcode/code_interviews_6/#9-61 "Permanent link") > 從撲克牌中隨機抽5張牌，判斷是不是一個順子，即這5張牌是不是連續的。2～10為數字本身，A為1，J為11，Q為12，K為13，而大、小王可以看成任意數字。 我們可以把5張牌看成由5個數字組成的數組。大、小王是特殊的數字，我們不妨把它們都定義為0，這樣就能和其他撲克牌區分開來了。 接下來我們分析怎樣判斷5個數字是不是連續的，最直觀的方法是把數組排序。值得注意的是，由于0可以當成任意數字，我們可以用0去補滿數組中的空缺。如果排序之后的數組不是連續的，即相鄰的兩個數字相隔若干個數字，那么只要我們有足夠的0可以補滿這兩個數字的空缺，這個數組實際上還是連續的。舉個例子，數組排序之后為{0, 1, 3, 4, 5}，在1和3之間空缺了一個2，剛好我們有一個0，也就是我們可以把它當成2去填補這個空缺。 于是我們需要做3件事情：首先把數組排序；其次統計數組中0的個數；最后統計排序之后的數組中相鄰數字之間的空缺總數。如果空缺的總數小于或者等于0的個數，那么這個數組就是連續的；反之則不連續。 最后我們還需要注意一點:如果數組中的非0數字重復出現，則該數組不是連續的。換成撲克牌的描述方式就是:如果一副牌里含有對子，則不可能是順子。 ~~~ private boolean isContinuous(int[] numbers) { if (numbers == null || numbers.length != 5) { return false; } final int length = numbers.length; Arrays.sort(numbers); int numberOfZero = 0; for (int i = 0; i < length && numbers[i] == 0; i++) { numberOfZero++; } int numberOfGap = 0; int small = numberOfZero; int big = small + 1; while (big < length) { if (numbers[small] == numbers[big]) return false; int gap = numbers[big] - numbers[small] - 1; numberOfGap += gap; small = big; big++; } return numberOfGap <= numberOfZero; } ~~~ 為了讓代碼顯得簡潔，上述代碼調用`Arrays.sort`進行排序。可能有人擔心時間復雜度是O(nlogn)，這還不夠快。由于撲克牌的值出現在0~13之間，我們可以定義一個長度為14的哈希表，這樣在O(n)時間內就能完成排序。通常我們認為不同級別的時間復雜度只有當n足夠大的時候才有意義。由于本題中數組的長度是固定的，只有5張牌，那么O(n)和O(nlogn)不會有多少區別，我們可以選用簡潔易懂的方法來實現算法。 ## 10\. (62)圓圈中最后剩下的數字[?](https://blog.yorek.xyz/leetcode/code_interviews_6/#10-62 "Permanent link") > 0, 1, …, n-1這n個數字排成一個圓圈，從數字0開始每次從這個圓圈里刪除第m個數字。求出這個圓圈里剩下的最后一個數字。 **解法一：用環形鏈表模擬圓圈** 此方法時間復雜度為O(mn)，空間復雜度為O(n)。 ~~~ private int lastRemaining1(int n, int m) { if (n <= 0 || m <= 0) { return -1; } ListNode head = new ListNode(0); ListNode p = head; for (int i = 1; i < n; i++) { p.next = new ListNode(i); p = p.next; } p.next = head; while (p.next != p) { for (int i = 0; i < m - 1; i++) { p = p.next; } p.next = p.next.next; } return p.value; } ~~~ **解法二：利用數學解法** 令方程f(n,m)表示每次在n個數字0,1,…,n-1中刪除第m個數后最后剩下的數字，也就是要求的結果。(m-1)%n為第一次被刪除的數字，記為k。 在刪除k之后剩下的n-1個數字為0,1,…,k-1,k+1,…,n-1，且下一次刪除的數字從k+1開始計數。相當于在剩下的序列中，k+1排在最前面，從而序列變成k+1,…,n-1,0,1,…k-1。由于這個序列的規律和最初的序列不一樣（最初的序列是從0開始的連續序列），所以記該函數為f(n-1,m)。由于這兩個需求最終結果一定是同一個數字，即f(n,m)=f(n-1,m)。 接下來我們把剩下的n-1數進行映射，使其形成0~n-2的序列。 k+1 -> 0 k+2 -> 1 … n-1 -> n-k-2 0 -> n-k-1 1 -> n-k … k-1 -> n-2 可以得到一個映射p,p(x)=(x-k-1)\\%n。其逆映射為p^{-1}(x)=(x+k+1)\\%n。 所以f(n-1,m)=p^{-1}\[f(n-1,m)\]=\[f(n-1,m)+k+1\]\\%n 代入k得f(n,m)=f(n-1,m)=\[f(n-1,m)+m\]\\%n 所以，我們可以得到下面這個遞推公式 f(n,m)=\\begin{cases} 0 & n=1 \\\\ \[f(n-1,m)+m\]\\%n & n>1 \\end{cases} ~~~ private int lastRemaining2(int n, int m) { if (n <= 0 || m <= 0) return -1; int last = 0; for (int i = 2; i <= n; i++) last = (last + m) % i; return last; } ~~~ 此方法時間復雜度為O(n)，空間復雜度為O(1)。 ## 11\. (63)股票的最大利潤[?](https://blog.yorek.xyz/leetcode/code_interviews_6/#11-63 "Permanent link") > 假設把某股票的價格按照時間先后順序存儲在數組中，請問買賣交易該股票可能獲得的利潤是多少？例如一只股票在某些時間節點的價格為{9, 11, 8, 5, 7, 12, 16, 14}。如果我們能在價格為5的時候買入并在價格為16時賣出，則能收獲最大的利潤11。 使用min保存前面的數據中最小的數，用當前的數減去最小數得到當前利潤，取當前利潤和之前最大利潤的最大值即可。 ~~~ private int maxDiff(int[] numbers) { if (numbers == null || numbers.length <= 1) { return 0; } int min = numbers[0]; int maxDiff = numbers[1] - min; for (int i = 2; i < numbers.length; i++) { if (numbers[i - 1] < min) { min = numbers[i - 1]; } int curDiff = numbers[i] - min; if (curDiff > maxDiff) { maxDiff = curDiff; } } return maxDiff; } ~~~ ## 12\. (64)求1+2+…+n[?](https://blog.yorek.xyz/leetcode/code_interviews_6/#12-6412n "Permanent link") > 求1+2+…+n，要求不能使用乘除法、for、while、if、else、switch、case等關鍵字及條件判斷語句（A?B:C）。 Warning 本題在C語言中有幾種解法，但在Java中不適用。 下面采取了遞歸的方式，并用短路與(&&)操作符判斷遞歸終止。 ~~~ private int solution(int n) { int sum = n; // n大于0時進行遞歸操作 // 后面的>0只是為了使后半部分構成一個布爾表達式 // 前面的boolean flag并無實際用途，只是為了讓編譯通過 boolean flag = (n > 0) && ((sum += solution(n - 1)) > 0); return sum; } ~~~ ## 13\. (65)不用加減乘除做加法[?](https://blog.yorek.xyz/leetcode/code_interviews_6/#13-65 "Permanent link") > 寫一個函數，求兩個整數之和，要求在函數體內不得使用＋、－、×、÷四則運算符號。 該題就是CPU中加法器的原理。 首先我們可以分析人們是如何做十進制加法的，比如是如何得出5+17=22這個結果的。實際上，我們可以分成三步進行：第一步只做各位相加不進位，此時相加的結果是12（個位數5和7相加不要進位是2，十位數0和1相加結果是1）；第二步做進位，5+7中有進位，進位的值是10；第三步把前面兩個結果加起來，12+10的結果是22，剛好5+17=22我們一直在想，求兩數之和四則運算都不能用，那還能用什么？對數字做運算，除四則運算之外，也就只剩下位運算了。位運算是針對ニ進制的，我們就以二進制再來分析一下前面的“三步走”策略對二進制是不是也適用。 5的二進制是101，17的二進制是10001。我們還是試著把計算分成三步:第一步各位相加但不計進位，得到的結果是10100（最后一位兩個數都是1，相加的結果是二進制的10。這一步不計進位，因此結果仍然是0）；第二步記下進位，在這個例子中只在最后一位相加時產生一個進位，結果是二進制的10；第三步把前兩步的結果相加，得到的結果是10110，轉換成十進制正好是22。由此可見“三步走”策略對二進制也是適用的。 接下來我們試著把二進制的加法用位運算來替代。第一步不考慮進位對每一位相加。0加0、1加1的結果都是0，0加1、1加0的結果都是1我們注意到，這和異或的結果是一樣的。對異或而言，0和0、1和1的異或結果是0，而0和1、1和0的異或結果是1。接著考慮第二步進位，對0加0、0加1、1加0而言，都不會產生進位，只有1加1時，會向前產生一個進位。此時我們可以想象成兩個數先做位與運算，然后再向左移動一位。只有兩個數都是1的時候，位與得到的結果是1，其余都是0。第三步把前兩個步驟的結果相加。第三步相加的過程依然是重復前面兩步，直到不產生進位為止。 ~~~ private int add(int num1, int num2) { int sum, carry; do { sum = num1 ^ num2; carry = (num1 & num2) << 1; num1 = sum; num2 = carry; } while (num2 != 0); return num1; } ~~~ 相關問題 不使用新的變量，交換兩個變量的值。比如有兩個變量a、b，我們希望交換它們的值。有兩種不同的方式： 基于加減法： a = a + b; b = a - b; a = a - b; 基于異或運算： a = a ^ b; b = a ^ b; a = a ^ b; ## 14\. (66)構建乘積數組[?](https://blog.yorek.xyz/leetcode/code_interviews_6/#14-66 "Permanent link") > 給定一個數組A\[0, 1, …, n-1\]，請構建一個數組B\[0, 1, …, n-1\]，其中B中的元素B\[i\] =A\[0\]×A\[1\]×… ×A\[i-1\]×A\[i+1\]×…×A\[n-1\]。不能使用除法。 如果沒有不能使用除法的限制，則可以用公式\\begin{matrix} \\prod\_{j=0}^{n-1} A\[j\]/A\[i\] \\end{matrix}求得B\[i\]。在使用除法時，要特別注意A\[i\]等于0的情況。 現在要求不能使用除法，只能用其他方法。一種直觀的解法是用連乘n-1個數字得到B\[i\]。顯然這種方法需要O(n^2)的時間構建整個數組B。 好在還有更高效的算法。可以把B\[i\]=A\[0\] \\times A\[1\] \\times \\cdots \\times A\[i-1\] \\times A\[i+1\] \\times \\cdots \\times A\[n-1\]看成A\[0\] \\times A\[1\] \\times \\cdots \\times A\[i-1\]和A\[i+1\] \\times \\cdots \\times A\[n-1\]兩部分的乘積。因此，數組B可以用一個矩陣來創建（見下圖）。在圖中，B\[i\]為矩陣中第i行所有元素的乘積。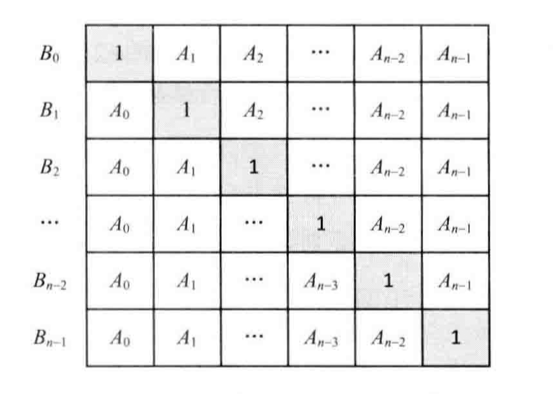  把數組B看成由一個矩陣來創建 不妨定義C\[i\]=A\[0\] \\times A\[1\] \\times \\cdots \\times A\[i-1\]，D\[i\]=A\[i+1\] \\times \\cdots \\times A\[n-1\]。C\[i\]可以用自上而下的順序計算出來，即C\[i\]=C\[i-1\] \\times A\[i-1\]。類似的，D\[i\]也可以用自下而上的順序計算出來，即D\[i\]=D\[i+1\] \\times A\[i+1\]。 顯然這種思路的時間復雜度是O(n)，這比蠻力法更高效。 ~~~ private void buildProductionArray(double[] input, double[] output) { if (input == null || output == null) { return; } int length1 = input.length; int length2 = output.length; if (length1 != length2 || length2 <= 1) { return; } output[0] = 1; for (int i = 1; i < length1; i++) output[i] = output[i - 1] * input[i - 1]; double temp = 1.0; for (int i = length1 - 2; i >= 0; i--) { temp *= input[i + 1]; output[i] *= temp; } } ~~~ ## 15\. (67)把字符串轉換成整數[?](https://blog.yorek.xyz/leetcode/code_interviews_6/#15-67 "Permanent link") > 請你寫一個函數StrToInt，實現把字符串轉換成整數這個功能。當然，不能使用atoi或者其他類似的庫函數。 此題同[LC-8-String to Integer (atoi)](https://blog.yorek.xyz/leetcode/leetcode1-10/#8-string-to-integer-atoi) 代碼粘貼如下： ~~~ class Solution { public int myAtoi(String str) { if (str == null) return 0; str = str.trim(); int i = 0; int sign = 1; if (i < str.length() && (str.charAt(i) == '+' || str.charAt(i) == '-')) { sign = str.charAt(i++) == '+' ? 1 : -1; } long result = 0; while (i < str.length() && Character.isDigit(str.charAt(i))) { result = 10 * result + (sign * (str.charAt(i++) - '0')); if (result >= Integer.MAX_VALUE) return Integer.MAX_VALUE; if (result <= Integer.MIN_VALUE) return Integer.MIN_VALUE; } return (int) result; } } ~~~ ## 16\. (68)樹中兩個結點的最低公共祖先[?](https://blog.yorek.xyz/leetcode/code_interviews_6/#16-68 "Permanent link") > 輸入兩個樹結點，求它們的最低公共祖先。 先求根節點到所給節點的路徑，然后問題轉化為求兩個鏈表的最后一個公共節點問題。 ~~~ private TreeNode getLastCommonParent(TreeNode root, TreeNode node1, TreeNode node2) { if (root == null || node1 == null || node2 == null) { return null; } List<TreeNode> path1 = new ArrayList<>(); getNodePath(root, node1, path1); List<TreeNode> path2 = new ArrayList<>(); getNodePath(root, node2, path2); return getLastCommonNode(path1, path2); } private boolean getNodePath(TreeNode root, TreeNode node, List<TreeNode> path) { if (root == node) { return true; } path.add(root); boolean found = false; for (int i = 0; !found && i < root.children.size(); i++) { found = getNodePath(root.children.get(i), node, path); } if (!found) { path.remove(path.size() - 1); } return found; } private TreeNode getLastCommonNode(List<TreeNode> path1, List<TreeNode> path2) { int i = 0, j = 0; TreeNode last = null; while (i < path1.size() && j < path2.size()) { if (path1.get(i) == path2.get(j)) { last = path1.get(i); } i++; j++; } return last; } ~~~