[TOC] ## 1\. 時間效率[?](https://blog.yorek.xyz/leetcode/code_interviews_5/#1 "Permanent link") ### 1.1 (39)數組中出現次數超過一半的數字[?](https://blog.yorek.xyz/leetcode/code_interviews_5/#11-39 "Permanent link") > 數組中有一個數字出現的次數超過數組長度的一半，請找出這個數字。例如輸入一個長度為9的數組{1, 2, 3, 2, 2, 2, 5, 4, 2}。由于數字2在數組中出現了5次，超過數組長度的一半，因此輸出2。 **解法一：基于partition函數的時間復雜度為O(n)的算法** 題目所給數組的特性：數組中有一個數字出現的次數超過了數組長度的一半。如果把這個數組排序，那么排序之后位于數組中間的數字一定就是那個出現次數超過數組長度一半的數字。也就是說，**這個數字是統計學上的中位數**，即長度為n的數組中第n/2大的數字。我們可以使用時間復雜度為O(n)的`partition`算法得到數組中任意第k大的數字。 這種算法受快速排序算法的啟發。在隨機快速排序算法中，我們先在數組中隨機選擇一個數字，然后調整數組中數字的順序，使得比選中的數字小的數字都排在它的左邊，比選中的數字大的數字都排在它的右邊。如果這個選中的數字的下標剛好是n/2，那么這個數字就是數組的中位數；如果它的下標大于n/2，那么中位數應該位于它的左邊，我們可以接著在它的左邊部分的數組中查找；如果它的下標小于n/2，那么中位數應該位于它的右邊，我們可以接著在它的右邊部分的數組中查找。這是一個典型的遞歸過程。 ~~~ private int moreThanHalfNum1(int[] numbers) { if (numbers == null) { throw new IllegalArgumentException("numbers不能為空"); } int middle = numbers.length >> 1; int start = 0; int end = numbers.length - 1; int index = QuickSort.partition(numbers, start, end); while (index != middle) { if (index > middle) { end = index - 1; index = QuickSort.partition(numbers, start, end); } else { start = index + 1; index = QuickSort.partition(numbers, start, end); } } int result = numbers[middle]; if (!checkMoreThanHalf(numbers, result)) { throw new IllegalArgumentException("結果不對"); } return result; } ~~~ **解法二：根據數組特點找出時間復雜度為O(n)的算法** 接下來我們從另外一個角度來解決這個問題。數組中有一個數字出現的次數超過數組長度的一半，也就是說出現的次數比其他所有數字出現次數的和還要多。因此，我們可以考慮在遍歷數組的時候保存兩個值：一個是數組中的一個數字；另一個是次數。當我們遍歷到下一個數字的時候，如果下一個數字和我們之前保存的數字相同，則次數加1；如果下一個數字和我們之前保存的數字不同，則次數減1。如果次數為零，那么我們需要保存下一個數字，并把次數設為1。由于我們要找的數字出現的次數比其他所有數字出現的次數之和還要多，那么要找的數字肯定是最后一次把次數設為1時對應的數字。 ~~~ private int moreThanHalfNum2(int[] numbers) { if (numbers == null) { throw new IllegalArgumentException("numbers不能為空"); } int result = numbers[0]; int cnt = 1; for (int i = 1; i < numbers.length; i++) { if (cnt == 0) { result = numbers[i]; cnt++; } else if (numbers[i] == result) { cnt++; } else { cnt--; } } if (!checkMoreThanHalf(numbers, result)) { throw new IllegalArgumentException("結果不對"); } return result; } ~~~ 解法比較 上述兩種算法的時間復雜度都是O(n)。基于partition函數的算法的時間復雜度的分析不是很直觀，本書限于篇幅不作詳細討論，感興趣的讀者可以參考《算法導論》等書籍的相關章節。我們注意到，在第一種解法中，需要交換數組中數字的順序，這就會修改輸入的數組。是不是可以修改輸入的數組呢？在面試的時候，我們可以和面試官討論，讓他明確需求。如果面試官說不能修改輸入的數組，那就只能采用第二種解法了。 另外，此題還可以采用笨方法，使用HashMap保存每個數出現的個數，時間復雜度也是O(n)。 ### 1.2 (40)最小的k個數[?](https://blog.yorek.xyz/leetcode/code_interviews_5/#12-40k "Permanent link") > 輸入n個整數，找出其中最小的k個數。例如輸入4、5、1、6、2、7、3、8這8個數字，則最小的4個數字是1、2、3、4。 **解法一：時間復雜度為O(n)，但需要修改輸入的數組** 我們同樣可以基于`partition`函數來解決這個問題。如果基于數組的第k個數字來調整，則使得比第k個數字小的所有數字都位于數組的左邊，比第k個數字大的所有數字都位于數組的右邊。這樣調整之后，位于數組中左邊的k個數字就是最小的k個數字（這k個數字不一定是排序的）。下面是基于這種思路的參考代碼: ~~~ private int[] getLeastNumbers1(int[] input, int k) { if (input == null || input.length < k || k <= 0) { return null; } int start = 0; int end = input.length - 1; int index = QuickSort.partition(input, start, end); while (index != k - 1) { if (index > k - 1) { end = index - 1; index = QuickSort.partition(input, start, end); } else { start = index + 1; index = QuickSort.partition(input, start, end); } } int[] result = new int[k]; System.arraycopy(input, 0, result, 0, k); return result; } ~~~ **解法二：時間復雜度為O(nlogk)的算法，特別適合處理海量數據** 我們可以先創建一個大小為k的數據容器來存儲最小的k個數字，接下來每次從輸入的n個整數中讀入一個數。如果容器中已有的數字少于k個，則直接把這次讀入的整數放入容器之中；如果容器中已有k個數字了，也就是容器已滿，此時我們不能再插入新的數字而只能替換已有的數字。找出這已有的k個數中的最大值，然后拿這次待插入的整數和最大值進行比較。如果待插入的值比當前已有的最大值小，則用這個數替換當前已有的最大值；如果待插入的值比當前已有的最大值還要大，那么這個數不可能是最小的k個整數之一，于是我們可以拋棄這個整數。 因此，當容器滿了之后，我們要做3件事情：一是在k個整數中找到最大數；二是有可能在這個容器中刪除最大數；三是有可能要插入一個新的數字。如果用一棵二叉樹來實現這個數據容器，那么我們能在O(logk)時間內實現這3步操作。因此，對于n個輸入數字而言，總的時間效率就是O(nlogk)。 我們可以選擇用不同的二叉樹來實現這個數據容器。由于每次都需要找到k個整數中的最大數字，我們很容易想到用最大堆。在最大堆中，根節點的值總是大于它的子樹中任意節點的值。于是我們每次可以在O(1)時間內得到已有的k個數字中的最大值，但需要O(logk)時間完成刪除及插入操作。 在Java中可以利用`PriorityQueue`實現最小堆、最大堆。 ~~~ // 最小堆 PriorityQueue<Integer> minHeap = new PriorityQueue<Integer>(); // 最大堆 PriorityQueue<Integer> maxHeap = new PriorityQueue<Integer>(n, new Comparator<Integer>(){ @Override public int compare(Integer o1, Integer o2) { return o2 - o1; } }); ~~~ 算法如下： ~~~ private int[] getLeastNumbers2(int[] input, int k) { if (input == null || input.length < k || k <= 0) { return null; } PriorityQueue<Integer> maxHeap = new PriorityQueue<>(k, new Comparator<Integer>() { @Override public int compare(Integer o1, Integer o2) { return o2 - o1; } }); for (int number: input) { if (maxHeap.size() < k) { maxHeap.offer(number); } else { if (number < maxHeap.peek()) { maxHeap.poll(); maxHeap.add(number); } } } int[] result = new int[k]; int index = 0; for (Object number: maxHeap.toArray()) { result[index++] = (Integer) number; } return result; } ~~~ ### 1.3 (41)數據流中的中位數[?](https://blog.yorek.xyz/leetcode/code_interviews_5/#13-41 "Permanent link") > 如何得到一個數據流中的中位數？如果從數據流中讀出奇數個數值，那么中位數就是所有數值排序之后位于中間的數值。如果從數據流中讀出偶數個數值，那么中位數就是所有數值排序之后中間兩個數的平均值。 由于數據是從一個數據流中讀出來的，因而數據的數目隨著時間的變化而增加。如果用一個數據容器來保存從流中讀出來的數據，則當有新的數據從流中讀出來時，這些數據就插入數據容器。這個數據容器用什么數據結構定義最合適呢？ 數組是最簡單的數據容器。如果數組沒有排序，則可以用`partition`函數找出數組中的中位數（詳見39）。在沒有排序的數組中插入一個數字和找出中位數的時間復雜度分別是O(1)和O(n)。 我們還可以在往數組里插入新數據時讓數組保持排序。這時由于可能需要移動O(n)個數，因此需要O(n)時間能完成插入操作。在已經排好序的數組中找出中位數是一個簡單的操作，只需要O(1)時間即可完成。 排序的鏈表是另外一種選擇。我們需要O(n)時間才能在鏈表中找到合適的位置插入新的數據。如果定義兩個指針指向鏈表中間的節點（如果鏈表的節點數目是奇數，那么這兩個指針指向同一個節點），那么可以在O(1)時間內得出中位數。此時的時間復雜度與基于排序的數組的時間復雜度一樣。 二叉搜索樹可以把插入新數據的平均時間降低到O(logn)。但是，當二叉搜索樹極度不平衡從而看起來像一個排序的鏈表時，插入新數據的時間仍然是O(n)。為了得到中位數，可以在二叉樹節點中添加一個表示子樹節點數目的字段。有了這個字段，可以在平均O(logn)時間內得到中位數，但最差情況仍然需要O(n )時間。 為了避免二叉搜索樹的最差情況，還可以利用平衡的二叉搜索樹，即AVL樹。通常AVL樹的平衡因子是左、右子樹的高度差。可以稍作修改，把AVL的平衡因子改為左、右子樹節點數目之差。有了這個改動，可以用O(logn)時間往AVL樹中添加一個新節點，同時用O(1)時間得到所有節點的中位數。 AVL樹的時間效率很高，但大部分編程語言的函數庫中都沒有實現這個數據結構。應聘者在短短幾十分鐘內實現AVL樹的插入操作是非常困難的。所以我們不得不分析還有沒有其他方法。 如下圖所示，如果數據在容器中已經排序，那么中位數可以由P1和P2指向的數得到。如果容器中數據的數目是奇數，那么P1和P2指向同一個數據。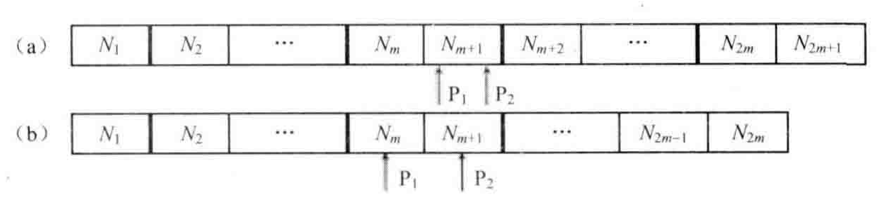  容器中數據被中間的一個或兩個數據分隔成為兩部分 我們注意到整個數據容器被分隔成兩部分。位于容器左邊部分的數據比右邊的數據小。另外，P1指向的數據是左邊部分最大的數，P2指向的數據是左邊部分最小的數。 如果能夠保證數據容器左邊的數據都小于右邊的數據，那么即使左、右兩邊內部的數據沒有排序，也可以根左邊最大的數及右邊最小的數得到中位數。如何快速從一個數據容器中找出最大數？用最大堆實現這個數據容器，因為位于堆頂的就是最大的數據。同樣，也可以快速從最小堆中找出最小數。 因此，可以用如下思路來解決這個問題：用一個最大堆實現左邊的數據容器，用一個最小堆實現右邊的數據容器。往堆中插入一個數據的時間效率是O(logn)。由于只需要O(1)時間就可以得到位于堆頂的數據，因此得到中位數的時間復雜度是O(1)。 下表總結了使用沒有排序的數組、排序的數組、排序的鏈表、二叉搜索樹、AVL數、最大堆和最小堆幾種不同的數據結構的時間復雜度。 | 數據結構 | 插入的時間復雜度 | 得到中位數的時間復雜度 | | --- | --- | --- | | 沒有排序的數據 | O(1) | O(n) | | 排序的數組 | O(n) | O(1) | | 排序的鏈表 | O(n) | O(1) | | 二叉搜索樹 | 平均O(logn)，最差O(n) | 平均O(logn)，最差O(n) | | AVL樹 | O(logn) | O(1) | | 最大堆和最小堆 | O(logn) | O(1) | **接下來考慮用最大堆和最小堆實現的一些細節。** 首先要保證數據平均分配到兩個堆中，因此兩個堆中數據的數目之差不能超過1。為了實現平均分配，可以在數據的總數目是偶數時把新數據插入最小堆，否則插入最大堆。 還要保證最大堆中的所有數據都要小于最小堆中的數據。當數據的總數目是偶數時，按照前面的分配規則會把新的數據插入最小堆。如果此時這個新的數據比最大堆中的一些數據要小，那該怎么辦呢？ 可以先把這個新的數據插入最大堆，接著把最大堆中最大的數字拿出來插入最小堆。由于最終插入最小堆的數字是原最大堆中最大的數字，這樣就保證了最小堆中所有數字都大于最大堆中的數字。 當需要把一個數據插入最大堆，但這個數據小于最小堆里的一些數據時，這個情形和前面類似。 ~~~ private PriorityQueue<Double> maxHeap = new PriorityQueue<>(new Comparator<Double>() { @Override public int compare(Double o1, Double o2) { if (o1.equals(o2)) return 0; else return o2 - o1 > 0 ? 1 : -1; } }); private PriorityQueue<Double> minHeap = new PriorityQueue<>(); private void insert(Double num) { if (((minHeap.size() + maxHeap.size()) & 1) == 0) { if (maxHeap.size() > 0 && num < maxHeap.peek()) { maxHeap.offer(num); num = maxHeap.poll(); } minHeap.offer(num); } else { if (minHeap.size() > 0 && num > minHeap.peek()) { minHeap.offer(num); num = minHeap.poll(); } maxHeap.offer(num); } } private double getMedian() { int size = maxHeap.size() + minHeap.size(); if (size == 0) { throw new IllegalStateException("No numbers are available"); } double median; if ((size & 1) == 1) { median = minHeap.peek(); } else { median = (minHeap.peek() + maxHeap.peek()) / 2; } return median; } ~~~ ### 1.4 (42)連續子數組的最大和[?](https://blog.yorek.xyz/leetcode/code_interviews_5/#14-42 "Permanent link") > 輸入一個整型數組，數組里有正數也有負數。數組中一個或連續的多個整數組成一個子數組。求所有子數組的和的最大值。要求時間復雜度為O(n)。 例如，輸入的數組為{1，-2，3，10，-4，7，2，5}，和最大的子數組為{3，10，-4，7，2}，因此輸出為該子數組的和18。 此題同[LC-53-Maximum Subarray](https://blog.yorek.xyz/leetcode/leetcode51-60/#53-maximum-subarray) **解法一：舉例分析數組的規律** 在分析上面例子的過程中，我們發現如果某步累加的結果不是正數，那么這些累加是可以拋棄的；否則可正常進行累加。在每步累加結束后存下這步最大的值。 ~~~ private int findGreatestSumOfSubArray(int[] data) { if (data == null || data.length == 0) { throw new IllegalArgumentException("data is empty"); } int currentSum = 0; int result = Integer.MIN_VALUE; for (int num: data) { if (currentSum <= 0) currentSum = num; else currentSum += num; if (currentSum > result) result = currentSum; } return result; } ~~~ **解法二：應用動態規劃法** 如果算法的功底足夠扎實，那么我們還可以用動態規劃的思想來分析這個問題。如果用函數f(i)表示以第i個數字結尾的子數組的最大和，那么我們需要求出max\[f(i)\]，其中0≤i<n。我們可用如下遞歸公式求f(i)： f(i)=\\begin{cases} data\[i\] & i=0或者f(i-1) \\leq 0 \\\\ f(i-1)+data\[i\] & i \\ne 0并且f(i-1)>0 \\end{cases} 這個公式的意義：當以第i-1個數字結尾的子數組中所有數字的和小于0時，如果把這個負數與第i個數累加，則得到的結果比第i個數字本身還要小，所以這種情況下以第i個數字結尾的子數組就是第i個數字本身。如果以第i-1個數字結尾的子數組中所有數字的和大于0，則與第i個數字累加就得到以第i個數字結尾的子數組中所有數字的和。 雖然通常我們用遞歸的方式分析動態規劃的問題，但最終都會基于循環去編碼。上述公式對應的代碼和前面給出的代碼一致。遞歸公式中的f(i)對應的變量是currentSum，而max\[f(i)\]就是result。因此，可以說這兩種思路是異曲同工的。 ### 1.5 (43)從1到n整數中1出現的次數[?](https://blog.yorek.xyz/leetcode/code_interviews_5/#15-431n1 "Permanent link") > 輸入一個整數n，求從1到n這n個整數的十進制表示中1出現的次數。例如輸入12，從1到12這些整數中包含1的數字有1、10、11和12，1一共出現了5次。 **不考慮時間效率的解法，不推薦** 最直觀的方法，也就是累加1~n中每個整數1出現的次數。我們可以每次通過對10求余樹判斷整數的個位數字是不是1。如果這個數大于10，則除以10之后再判斷個位數字是不是1。 如果輸入數字n，n有O(logn)位，我們需要判斷每一位是不是1，那么它的時間復雜度是O(nlogn)。 ~~~ private int numberOf1Between1AndN_Solution1(int n) { if (n <= 0) return 0; int number = 0; for (int i = 1; i <= n; i++) { number += countNumber(i); } return number; } private int countNumber(int n) { int cnt = 0; while (n != 0) { if (n % 10 == 1) { cnt++; } n /= 10; } return cnt; } ~~~ **從數字規律著手明顯提高時間效率的解法** 如果希望不用計算每個數字的1的個數，那就只能去尋找1在數字中出現的規律了。為了找到規律，我們不妨用一個稍微大一點的數字如21345作為例子來分析。我們把1~21345的所有數字分為兩段:一段是1~1345另一段是1346~21345。 我們先看1346~21345中1出現的次數。1的出現分為兩種情況。**首先分析1出現在最高位（本例中是萬位）的情況**。在1346~21345的數字中，1出現在10000~19999這10000個數字的萬位中，一共出現了10000（10^4）次。 值得注意的是，并不是對所有5位數而言在萬位出現的次數都是10000次。對于萬位是1的數字如輸入12345，1只出現在10000~12345的萬位，出現的次數不是10^4次，而是2346次，也就是除去最高數字之后剩下的數字再加上1（2345+1=2346次）。 **接下來分析1出現在除最高位之外的其他4位數中的情況**。例子中1346~21345這20000個數字中后4位中1出現的次數是8000次。由于最高位是2，我們可以再把1346~21345分成兩段:1346~11345和11346~21345。每一段剩下的4位數字中，選擇其中一位是1，其余三位可以在0~9這10個數字中任意選擇，因此根據排列組合原則，總共出現的次數是2×4×10^3=8000次。 **至于在1~1345中1出現的次數**，我們就可以用遞歸求得了。這也是我們為什么要把1~21345分成1~134和1346~21345兩段的原因。因為把21345的最高位去掉就變成1345，便于我們采用遞歸的思路。 這種思路是每次去掉最高位進行遞歸遞歸的次數和位數相同。一個數字n有O(logn)位，因此這種思路的時間復雜度是O(logn)，比前面的原始方法要好很多。 ~~~ private int numberOf1Between1AndN_Solution2(int n) { if (n <= 0) return 0; char[] strN = String.valueOf(n).toCharArray(); return numberOf1(strN, 0); } private int numberOf1(char[] str, int begin) { if (str == null || str.length <= begin || str[begin] < '0' || str[begin] > '9') { return 0; } int first = str[begin] - '0'; int length = str.length - begin; if (length == 1 && first == 0) return 0; if (length == 1 && first > 0) return 1; // 最高位為1的情況 int numberFirstDigit = 0; if (first > 1) numberFirstDigit = (int) Math.pow(10, length - 1); else if (first == 1) numberFirstDigit = Integer.parseInt(new String(str, begin + 1, length - 1)) + 1; // 其他位置為1的情況 int numOtherDigit = first * (length - 1) * (int) Math.pow(10, length - 2); // 遞歸部分 int numRecursive = numberOf1(str, begin + 1); return numberFirstDigit + numOtherDigit + numRecursive; } ~~~ ### 1.6 (44)數字序列中某一位的數字[?](https://blog.yorek.xyz/leetcode/code_interviews_5/#16-44 "Permanent link") > 數字以0123456789101112131415…的格式序列化到一個字符序列中。在這個序列中，第5位（從0開始計數）是5，第13位是1，第19位是4，等等。請寫一個函數求任意位對應的數字。 *題目意思是將從0至正無窮的整數依次排列到一個字符串中，求這個字符串的第n位是什么數字。* 我們用一個具體的例子來分析如何解決這個問題。比如，序列的第1001位是什么？ 序列的前10位是0~9這10個只有一位的數字。顯然第1001位在這10個數字之后，因此這10個數字可以直接跳過。我們再從后面緊跟著的序列中找第991（991=1001-10）位的數字。 接下來180位數字是90個10~99的兩位數。由于991>180，所以第991位在所有的兩位數之后。我們再跳過90個兩位數，繼續從后面找881（881=991-180）位。 接下來的2700位是900個100~999的三位數。由于811<2700，所以第811位是某個三位數中的一位。由于811=270×3+1，這意味著第811位是從100開始的第270個數字即370的中間一位，也就是7。 算法如下： ~~~ private int digitAtIndex(int index) { if (index < 0) return -1; int digits = 1; while (true) { int numbers = countOfIntegers(digits); if (index < numbers * digits) return digitAtIndex(index, digits); index -= digits * numbers; digits++; } } /** * digits位數的數字總共有多少個 * 2(10~99) -> 90 * 3(100~999) -> 900 */ private int countOfIntegers(int digits) { if (digits == 1) return 10; int count = (int) Math.pow(10, digits - 1); return 9 * count; } /** * 要找的數在digits位數中的位置 */ private int digitAtIndex(int index, int digits) { // 先獲取到所求位置對應的整數 int number = beginNumber(digits) + index / digits; // 計算所求位置是整數的第幾位 int indexFromRight = digits - index % digits; // 獲取對應位置的數字 for (int i = 1; i < indexFromRight; i++) number /= 10; return number % 10; } /** * digits位數的第一個數字 */ private int beginNumber(int digits) { if (digits == 1) return 0; return (int) Math.pow(10, digits - 1); } ~~~ ### 1.7 (45)把數組排成最小的數[?](https://blog.yorek.xyz/leetcode/code_interviews_5/#17-45 "Permanent link") > 輸入一個正整數數組，把數組里所有數字拼接起來排成一個數，打印能拼接出的所有數字中最小的一個。例如輸入數組{3, 32, 321}，則打印出這3個數字能排成的最小數字321323。 這道題最直接的解法應該是先求出這個數組中所有數字的全排列，然后把每個排列拼起來，最后求出拼起來的數字的最小值。求數組的排列和第38題“字符串的排列”非常類似，這里不再詳細介紹。根據排列組合的知識，n個數字總共有n!個排列。我們再來看一種更快的算法。 這道題其實是希望我們能找到一個排序規則，數組根據這個規則排序之后能排成一個最小的數字。要確定排序規則，就要比較兩個數字，也就是給出兩個數字m和n，我們需要確定一個規則判斷m和n哪個應該排在前面，而不是僅僅比較這兩個數字的值哪個更大。 根據題目的要求，兩個數字m和n能拼接成數字mn和nm。如果mn”及“=”表示常規意義的數值的大小關系，而文字“大于”、“小于”、“等于”表示我們新定義的大小關系。 接下來考慮怎么去拼接數字，即給出數字m和n，怎么得到數字mn和nm并比較它們的大小。直接用數值去計算不難辦到，但需要考慮的一個潛在問題就是m和n都在int型能表達的范圍內，但把它們拼接起來的數字mn和nm用int型表示就有可能溢出了，**所以這還是一個隱形的大數問題**。 一個非常直觀的解決大數問題的方法就是把數字轉換成字符串。另外，由于把數字m和n拼接起來得到mn和nm，它們的位數肯定是相同的，因此比較它們的大小只需要按照字符串大小的比較規則就可以了。 ~~~ private void printMinNumber(int[] numbers) { if (numbers == null || numbers.length == 0) { return; } final int n = numbers.length; String[] strNumbers = new String[n]; for (int i = 0; i < n; i++) strNumbers[i] = String.valueOf(numbers[i]); Arrays.sort(strNumbers, new Comparator<String>() { @Override public int compare(String o1, String o2) { String str1 = o1 + o2; String str2 = o2 + o1; return str1.compareTo(str2); } }); for (String str: strNumbers) System.out.printf("%s", str); System.out.println(); } ~~~ 在上述代碼中，我們先把數組中的整數通過`String.valueOf(int)`轉換成字符串，然后在調用`Arrays.sort(T[], Comparator<? super T>)`排序，最后把排好序的數組中的數字依次打印出來，就是該數組中數字能拼接出來的最小數字。這種思路的時間復雜度和快速排序的時間復雜度相同，也就是O(nlogn)，這比用n!的時間求出所有排列的思路要好很多。 在上述思路中，我們定義了一種新的比較兩個數字大小的規則，這種規則是不是有效的？另外，我們只是定義了比較兩個數字大小的規則，卻用它來排序一個含有多個數字的數組，最終拼接數組中的所有數字得到的是不是真的就是最小的數字？一些嚴格的面試官還會要求我們給出嚴格的數學證明，以確保我們的解決方案是正確的。 我們首先證明之前定義的比較兩個數字大小的規則是有效的。一個有效的比較規則需要3個條件：自反性、對稱性和傳遞性。我們分別予以證明。 1. 自反性：顯然有aa=aa，所以a等于a。 2. 對稱性：如果a小于b，則abab，因此b大于a。 3. 傳遞性：如果a小于b，則ab<ba。假設a和b用十進制表示時分別有l位和m位，于是ab=a\\times10^m+b，ba=b\\times10^l+a。 ab<ba→a\\times10^m+b<b\\times10^l+a→a\\times10^m-a<b\\times10^l-b→ a(10^m-1)<b(10^l-1)→a/(10^l-1)<b/(10^m-1) 同理，如果b小于c，則bc<cb。假設c用十進制表示時有n位，和前面的證明過程一樣，可以得到b/(10^m-1)<c/(10^n-1)。 a/(10^l-1)<b/(10^m-1) 且 b/(10^m-1)<c/(10^n-1)→\\\\a/(10^l-1)<c/(10^n-1)→a(10^n-1)<c(10^l-1)→ a\\times10^n+c<c\\times10^l+a→ac<ca→a<c 于是我們證明了這種比較規則滿足自反性、對稱性和傳遞性，是一種有效的比較規則。接下來我們證明根據這種比較規則把數組排序之后，把數組中的所有數字拼接起來得到的數字的確是最小的。直接證明不是很容易，我們不妨用反證法來證明。 我們把n個數按照前面的排序規則排序之后，表示為A\_1A\_2A\_3 \\ldots A\_n。假設這樣拼接出來的數字并不是最小的，即至少存在兩個x和y(0<x<y<n)，交換第x個數和第y個數后，A\_1A\_2 \\ldots A\_y \\ldots A\_x \\ldots A\_n<A\_1A\_2 \\ldots A\_x \\ldots A\_y \\ldots A\_n。 由于A\_1A\_2 \\ldots A\_x \\ldots A\_y \\ldots A\_n是按照前面的規則排好的序列，所以有A\_x小于A\_{x+1}小于A\_{x+2}\\ldots 小于A\_{y-2}小于A\_{y-1}小于A\_y。 由于A\_{y-1}小于A\_y，所以A\_{y-1}A\_y<A\_yA\_{y-1}。我們在序列A\_1A\_2 \\ldots A\_x \\ldots A\_{y-1}A\_y \\ldots A\_n中交換A\_{y-1}和A\_y，有A\_1A\_2 \\ldots A\_x \\ldots A\_{y-1}A\_y \\ldots A\_n<A\_1A\_2 \\ldots A\_x \\ldots A\_yA\_{y-1} \\ldots A\_n（這個實際上也需要證明，感興趣的讀者可以自己試著證明）。我們就這樣一直把A\_y和前面的數字交換，直到和A\_x交換為止。于是就有 A\_1A\_2 \\ldots A\_x \\ldots A\_{y-1}A\_y \\ldots A\_n<A\_1A\_2 \\ldots A\_x \\ldots A\_yA\_{y-1} \\ldots A\_n< \\\\ A\_1A\_2 \\ldots A\_x \\ldots A\_yA\_{y-2}A\_{y-1} \\ldots A\_n< \\ldots <A\_1A\_2 \\ldots A\_yA\_x \\ldots A\_{y-2}A\_{y-1} \\ldots A\_n 同理，由于A\_x小于A\_{x+1}，所以A\_xA\_{x+1}<A\_{x+1}A\_x。我們在序列A\_1A\_2 \\ldots A\_yA\_xA\_{x+1} \\ldots A\_{y-2}A\_{y-1} \\ldots A\_n中只交換A\_x和A\_{x+1}，有A\_1A\_2 \\ldots A\_yA\_xA\_{x+1} \\ldots A\_{y-2}A\_{y-1} \\ldots An<A\_1A\_2 \\ldots A\_yA\_{x+1}A\_x \\ldots A\_{y-2}A\_{y-1} \\ldots An。接下來一直拿A\_x和它后面的數字交換，直到和A\_{y-1}交換為止。于是就有 A\_1A\_2 \\ldots A\_yA\_xA\_{x+1} \\ldots A\_{y-2}A\_{y-1} \\ldots An<A\_1A\_2 \\ldots A\_yA\_{x+1}A\_x \\ldots A\_{y-2}A\_{y-1} \\ldots An<\\\\ \\ldots <A\_1A\_2 \\ldots A\_yA\_{x+1}A\_{x+2} \\ldots A\_{y-2}A\_{y-1}A\_x \\ldots A\_n。 所以A\_1A\_2 \\ldots A\_x \\ldots A\_y \\ldots A\_n<A\_1A\_2 \\ldots A\_y \\ldots A\_x \\ldots A\_n，這和我們的假設A\_1A\_2 \\ldots A\_y \\ldots A\_x \\ldots A\_n<A\_1A\_2 \\ldots A\_x \\ldots A\_y \\ldots A\_n相矛盾。 所以假設不成立，我們的算法是正確的。 ### 1.8 (46)把數字翻譯成字符串[?](https://blog.yorek.xyz/leetcode/code_interviews_5/#18-46 "Permanent link") > 給定一個數字，我們按照如下規則把它翻譯為字符串：0翻譯成"a"，1翻譯成"b"，……，11翻譯成"l"，……，25翻譯成"z"。一個數字可能有多個翻譯。例如12258有5種不同的翻譯，它們分別是"bccfi"、"bwfi"、"bczi"、"mcfi"和"mzi"。請編程實現一個函數用來計算一個數字有多少種不同的翻譯方法。 我們以12258為例分析如何從數字的第一位開始一步步計算不同翻譯方法的數目。我們有兩種不同的選擇來翻譯第一位數字1。第一種選擇是數字1單獨翻譯成“b”，后面剩下數字2258；第二種選擇是1和緊挨著的2一起翻譯成“m”，后面剩下數字258。 當最開始的一個或者兩個數字被翻譯成一個字符之后，我們接著翻譯后面剩下的數字。顯然，我們可以寫個遞歸函數來計算翻譯的數目。 我們定義函數f(i)表示從第i位數字開始的不同翻譯的數目，那么f(i)=f(i+1)+g(i,i+1) \\times f(i+2)。當第i位和第i+1位兩位數字拼接起來的數字在10~25的范圍內時，函數g(i, i+1)的值為1；否則為0。 盡管我們用遞歸的思路來分析這個問題，但由于存在重復的子問題，遞歸并不是解決這個問題的最佳方法。還是以12258為例。如前所述，翻譯12258可以分解成兩個子問題：翻譯1和2258，以及翻譯12和258。接下來我們翻譯第一個子問題中剩下的2258，同樣也可以分解成兩個自問題:翻譯2和258，以及翻譯22和58。注意到子問題翻譯258重復出現了。 **遞歸從最大的問題開始自上而下解決問題。我們也可以從最小的子問題開始自下而上解決問題，這樣就可以消除重復的子問題**。 也就是說，我們從數字的末尾開始，然后從右到左翻譯并計算不同翻譯的數目。 ~~~ private int getTranslationCount(int number) { if (number < 0) return 0; return getTranslationCount(String.valueOf(number).toCharArray()); } private int getTranslationCount(char[] number) { int length = number.length; int[] counts = new int[length]; int count; for (int i = length - 1; i >= 0; i--) { if (i < length - 1) count = counts[i + 1]; else count = 1; if (i < length - 1) { int digit1 = number[i] - '0'; int digit2 = number[i + 1] - '0'; int converted = digit1 * 10 + digit2; if (converted >= 10 && converted <= 25) { if (i < length - 2) count += counts[i + 2]; else count++; } } counts[i] = count; } count = counts[0]; return count; } ~~~ ### 1.9 (47)禮物的最大價值[?](https://blog.yorek.xyz/leetcode/code_interviews_5/#19-47 "Permanent link") > 在一個m×n的棋盤的每一格都放有一個禮物，每個禮物都有一定的價值（價值大于0）。你可以從棋盤的左上角開始拿格子里的禮物，并每次向左或者向下移動一格直到到達棋盤的右下角。給定一個棋盤及其上面的禮物，請計算你最多能拿到多少價值的禮物？ [LC-64-Minimum Path Sum](https://blog.yorek.xyz/leetcode/leetcode61-70/#64-minimum-path-sum) 例如，在下面的棋盤中，如果沿著帶下畫線的數字的線路（1、12、5、7、7、16、5），那么我們能拿到最大價值為53的禮物。  這是一個典型的能用動態規劃解決的問題。我們先用遞歸的思路來分析。我們先定義第一個函數f(i,j)表示到達坐標為(i,j)的格子時能拿到的禮物總和的最大值。根據題目要求，我們有兩種可能的途徑到達坐標為(i,j)的格 子：通過格子(i-1,j)或者(i,j-1).所以f(i,j)\=max(f(i-1,j),f(i,j-1))+gift\[i,j\]。gift\[i,j\]表示坐標為(i,j)的格子里禮物的價值。 盡管我們用遞歸來分析問題，但由于有大量重復的計算，導致遞歸的代碼并不是最優的。相對而言，基于循環的代碼效率要高很多。為了緩存中間計算結果，我們需要一個輔助的二維數組。數組中坐標為(i,j)的元素表示到達坐標為(i,j)的格子時能拿到的禮物價值總和的最大值。 ~~~ int getMaxValue_solution1(int[][] values, int rows, int cols) { if (values == null || rows <= 0 || cols <= 0) return 0; int[][] maxValues = new int[rows][cols]; for (int i = 0; i < rows; i++) { for (int j = 0; j < cols; j++) { int up = 0; int left = 0; if (i > 0) up = maxValues[i - 1][j]; if (j > 0) left = maxValues[i][j - 1]; maxValues[i][j] = Math.max(up, left) + values[i][j]; } } return maxValues[rows - 1][cols - 1]; } ~~~ 接下來我們考慮進一步的優化。前面我們提到，到達坐標為(i,j)的格子時能夠拿到的禮物的最大價值只依賴坐標為(i-1,j)和(i,j-1)的兩個格子，因此第i-2行及更上面的所有格子禮物的最大價值實際上沒有必要保存下來。我們可以用一個一維數組來替代前面代碼中的二維矩陣maxValues。該一維數組的長度為棋盤的列數n。當我們計算到達坐標為(i,j)的格子時能夠拿到的禮物的最大價值f(i,j)，數組中前j個數字分別是f(i,0),f(i,1), \\ldots ,f(i,j-1)，數組從下標為j的數字開始到最后一個數字，分別為f(i-1,j),f(i-1,j+1), \\ldots ,f(i-1,n-1)。也就是說，該數組前面j個數字分別是當前第i行前面j個格子禮物的最大價值，而之后的數字分別保存前面第i-1行n-j個格子禮物的最大價值。 ~~~ int getMaxValue_solution2(int[][] values, int rows, int cols) { if (values == null || rows <= 0 || cols <= 0) return 0; int[] maxValues = new int[cols]; for (int i = 0; i < rows; i++) { for (int j = 0; j < cols; j++) { int up = 0, left = 0; if (i > 0) up = maxValues[j]; if (j > 0) left = maxValues[j - 1]; maxValues[j] = Math.max(up, left) + values[i][j]; } } return maxValues[cols - 1]; } ~~~ ### 1.10 (48)最長不含重復字符的子字符串[?](https://blog.yorek.xyz/leetcode/code_interviews_5/#110-48 "Permanent link") > 請從字符串中找出一個最長的不包含重復字符的子字符串，計算該最長子字符串的長度。假設字符串中只包含從'a'到'z'的字符。 此題同[LC-3-Longest Substring Without Repeating Characters](https://blog.yorek.xyz/leetcode/leetcode1-10/#3-longest-substring-without-repeating-characters) 直接上對應代碼 ~~~ private int longestSubstringWithoutDuplication(String str) { if (str == null || str.length() == 0) { return 0; } final int n = str.length(); Set<Character> set = new HashSet<>(); int ans = 0, i = 0, j = 0; while (i < n && j < n) { // try to extend the range [i, j] if (!set.contains(str.charAt(j))){ set.add(str.charAt(j++)); ans = Math.max(ans, j - i); } else { set.remove(str.charAt(i++)); } } return ans; } ~~~ ## 2\. 時間效率與空間效率的平衡[?](https://blog.yorek.xyz/leetcode/code_interviews_5/#2 "Permanent link") 硬件的發展一直遵循摩爾定律，內存的容量基本上每隔18個月就會翻一番。由于內存的容量增加迅速，在軟件開發的過程中我們允許以犧牲一定的空間為代價來優化時間性能，以盡可能地縮短軟件的響應時間。這就是我們通常所說的“以空間換時間”。 在面試的時候，如果我們分配少量的輔助空間來保存計算的中間結果以提高時間效率，則通常是可以被接受的。本書中收集的面試題中有不少這種類型的題目，比如在面試題49“丑數”中用一個數組按照從小到大的順序保存已經求出的丑數；在面試題60“n個骰子的點數”中交替使用兩個數組求骰子每個點數出現的次數。 值得注意的是，“以空間換時間”的策略并不一定都是可行的，在面試的時候要具體問題具體分析。我們都知道在n個無序的元素里執行查找操作，需要O(n)的時間。但如果我們把這些元素放進一個哈希表，那么在哈希表內就能實現時間復雜度為O(1)的查找。但同時實現一個哈希表是有空間消耗的，是不是值得以多消耗空間為前提來換取時間性能的提升，我們需要根據實際情況仔細權衡。在面試題50“第一個只出現一次的字符”中，我們用數組實現了一個簡易哈希表，有了這個哈希表就能實現在O(1)時間內查找任意字符。對于ASCI碼的字符而言，總共只有256個字符，因此只需要1KB的輔助內存。這點內存消耗對于絕大多數硬件來說是完全可以接受的。但如果是16位的 Unicode的字符，創建這樣一個長度為216的整型數組需要4×216也就是256KB的內存。這對于個人計算機來說也是可以接受的，但對于一些嵌入式的開發就要慎重了。 很多時候時間效率和空間效率存在類似于魚與熊掌的關系，我們需要在它們之間有所取舍。在面試的時候究竟是“以時間換空間”還是“以空間換時間”，我們可以和面試官進行探討。多和面試官進行這方面的討論是很有必要的，這既能顯示我們的溝通能力，又能展示我們對軟件性能全方位的把握能力。 ### 2.1 (49)丑數[?](https://blog.yorek.xyz/leetcode/code_interviews_5/#21-49 "Permanent link") > 我們把只包含因子2、3和5的數稱作丑數（Ugly Number）。求按從小到大的順序的第1500個丑數。例如6、8都是丑數，但14不是，因為它包含因子7。習慣上我們把1當做第一個丑數。 **逐個判斷每個整數是不是丑數的解法，直觀但不夠高效** 所謂一個數m是另一個數n的因子，是指n能被m整除，也就是n％m=0。根據丑數的定義，丑數只能被2、3和5整除。也就是說，如果一個數能被2整除，就連續除以2；如果能被3整除，就連續除以3；如果能被5整除，就除以連續5。如果最后得到的1，那么這個數就是丑數；否則不是。 我們可以得到下面的代碼： ~~~ private int getUglyNumber1(int number) { if (number <= 0) return 0; int cnt = 0; int index = 0; while (cnt < number) { index++; if (isUgly(index)) { cnt++; } } return index; } private boolean isUgly(int number) { while (number % 2 == 0) number /= 2; while (number % 3 == 0) number /= 3; while (number % 5 == 0) number /= 5; return number == 1; } ~~~ **創建數組保存已經找到的丑數，用空間換時間的解法** 前面的算法之所以效率低，很大程度上是因為不管一個數是不是丑數，我們都要對它進行計算。接下來我們試著找到一種只計算丑數的方法，而不在非丑數的整數上花費時間。**根據丑數的定義，丑數應該是另一個丑數乘以2、3或者5的結果（1除外）**。因此，我們可以創建一個數組，里面的數字是排好序的丑數，每個丑數都是前面的丑數乘以2、3或者5得到的。 這種思路的關鍵在于怎樣確保數組里面的丑數是排好序的。假設數組中已經有若干個排好序的丑數，并且把已有最大的丑數記作M，接下來分析如何生成下一個丑數。該丑數肯定是前面某一個丑數乘以2、3或者5的結果，所以我們首先考慮把已有的每個丑數乘以2。在乘以2的時候，能得到若干個小于或等于M的結果。由于是按照順序生成的，小于或者等于M肯定已經在數組中了，我們不需再次考慮；還會得到若干個大于M的結果，但我們只需要第一個大于M的結果，因為我們希望丑數是按從小到大的順序生成的，其他更大的結果以后再說。我們把得到的第一個乘以2后大于M的結果記為M\_2。同樣，我們把已有的每個丑數乘以3和5，能得到第一個大于M的結果M\_3和M\_5。那么下一個丑數應該是M\_2、M\_3和M\_5這3個數的最小者。 在前面分析的時候提到把已有的每個丑數分別乘以2、3和5事實上這不是必需的，因為已有的丑數是按順序存放在數組中的。對于乘以2而言，肯定存在某一個丑數T\_2，排在它之前的每個丑數乘以2得到的結果都會小于已有最大的丑數，在它之后的每個丑數乘以2得到的結果都會太大。我們只需記下這個丑數的位置，同時每次生成新的丑數的時候去更新這個T\_2即可。對于乘以3和5而言，也存在同樣的T\_3和T\_5。 ~~~ private int getUglyNumber2(int number) { if (number <= 0) return 0; int[] uglyNumbers = new int[number]; uglyNumbers[0] = 1; int nextUglyIndex = 1; int index2 = 0, index3 = 0, index5 = 0; while (nextUglyIndex < number) { int min = min(uglyNumbers[index2] * 2, uglyNumbers[index3] * 3, uglyNumbers[index5] * 5); uglyNumbers[nextUglyIndex] = min; while (uglyNumbers[index2] * 2 <= min) index2++; while (uglyNumbers[index3] * 3 <= min) index3++; while (uglyNumbers[index5] * 5 <= min) index5++; nextUglyIndex++; } return uglyNumbers[nextUglyIndex - 1]; } private int min(int a, int b, int c) { return Math.min(Math.min(a, b), c); } ~~~ 和第一種思路相比，第二種思路不需要在非丑數的整數上進行任何計算，因此時間效率有明顯提升。但也需要指出，第二種算法由于需要保存已經生成的丑數，則因此需要一個數組，從而增加了空間消耗。如果是求第1500個丑數，則將創建一個能容納1500個丑數的數組，這個數組占據6KB的內容空間。而第一種思路沒有這樣的內存開銷。總的來說，第二種思路相當于用較小的空間消耗換取了時間效率的提升。 ### 2.2 (50)第一個只出現一次的字符[?](https://blog.yorek.xyz/leetcode/code_interviews_5/#22-50 "Permanent link") #### 2.2.1 字符串中第一個只出現一次的字符[?](https://blog.yorek.xyz/leetcode/code_interviews_5/#221 "Permanent link") > 在字符串中找出第一個只出現一次的字符。如輸入"abaccdeff"，則輸出'b'。 由于題目與字符出現的次數相關，那么我們是不是可以統計每個字符在該字符串中出現的次數？要達到這個目的，我們需要一個數據容器來存放每個字符的出現次數。在這個數據容器中，可以根據字符來查找它出現的次數，也就是說這個容器的作用是把一個字符映射成一個數字。在常用的數據容器中，哈希表正是這個用途。 為了解決這個問題，我們可以定義哈希表的鍵值（key）是字符，而值（value）是該字符出現的次數。同時我們還需要從頭開始掃描字符串兩次。第一次掃描字符串時，每掃描到一個字符，就在哈希表的對應項中把次數加1。接下來第二次掃描時，每掃描到一個字符，就能從哈希表中得到該字符出現的次數。這樣，第一個只出現一次的字符就是符合要求的輸出。 由于本題的特殊性，我們其實只需要一個非常簡單的哈希表就能滿足要求，因此我們可以考慮實現一個簡單的哈希表。字符(char)是一個長度為8的數據類型，因此總共有256種可能。于是我們創建一個長度為256的數組，每個字母根據其ASCII碼值作為數組的下標對應數組的一個數字，而數組中存儲的是每個字符出現的次數。這樣我們就創建了一個大小為256、以字符ASCII碼為鍵值的哈希表。 第一次掃描時，在哈希表中更新一個字符出現的次數的時間是O(1)。如果字符串長度為n，那么第一次掃描的時間復雜度是O(n)。第二次掃描時，同樣在O(1)時間內能讀出一個字符出現的次數，所以時間復雜度仍然是O(n)。這樣算起來，總的時間復雜度是O(n)。同時，我們需要一個包含256個字符的輔助數組，它的大小是1KB由于這個數組的大小是一個常數，因此可以認為這種算法的空間復雜度是O(1)。 Warning **注意**：本書原版是C語言編寫的，char在Java中占用兩個byte，共16個bit。 下面的解法要求每個字符都是小寫字母，如果出現其他字符那么該解法不適用。可以將n設置成2^16或者使用完整的哈希表代替自己實現的簡單哈希表。 ~~~ private char firstNotRepeatingChar(String str) { if (str == null || str.length() == 0) { return ' '; } final int n = 26; int[] hashTable = new int[n]; for (int i = 0; i < str.length(); i++) { char ch = str.charAt(i); hashTable[ch - 'a']++; } for (int i = 0; i < str.length(); i++) { char ch = str.charAt(i); if (hashTable[ch - 'a'] == 1) { return ch; } } return ' '; } ~~~ 本題擴展 在前面的例子中，我們之所以可以把哈希表的大小設為256，是因為字符(char)是8bit的類型，總共只有256個字符。但實際上字符不只是256個，比如中文就有幾千個漢字。如果題目要求考慮漢字，那么前面的算法是不是有問題？如果有，則可以怎么解決？ *在Java中漢字也可以使用char表示，此時將n設置成2^16或者使用完整的哈希表代替自己實現的簡單哈希表都可以。如果加大n，在映射時直接使用hashTable\[ch\]即可。* 相關題目 定義一個函數，輸入兩個字符串，從第一個字符串中刪除在第二個字符串中出現過的所有字符。例如，從第一個字符串"We are student."中刪除在第二個字符串"saeiou"出現過的字符得到的結果是"Wr Stdnts."。 *為了解決這個問題，我們可以創建一個用數組實現的簡單哈希表來存儲第二個字符串。這樣我們從頭到尾掃描第一個字符串的每個字符時，用O(1)時間就能判斷出該字符是不是在第二個字符串中。如果第一個字符串的長度是n，那么總的時間復雜度是O(n)。* 相關題目 定義一個函數，刪除字符串中所有重復出現的字符。例如，輸入"google"，刪除重復的字符之后的結果是"gole"。 *這道題目和上面的問題比較類似，我們可以創建一個用布爾型數組實現的簡單的哈希表。數組中的元素的意義是其下標看作ASCII碼后對應的字母在字符串中是否已經出現。我們先把數組中所有的元素都設為false。以"google"為例，當掃描到第一個g時，g的ASCII碼是103，那么我們把數組中下標為103的元素設為true。當掃描到第二個g時，我們發現數組中下標為103的元素的值是true，就知道g在前面經出現過。也就是說，我們用O(1)時間就能判斷出每個字符是否在前面已經出現過。如果字符串的長度n，那么總的時間復雜度是O(n)。* 相關題目 在英語中，如果兩個單詞中出現的字母相同，并且每個字母出現的次數也相同，那么這兩個單詞互為變位詞(Anagram)。例如，silent與listen、evil與live等互為變位詞。請完成一個函數，判斷輸入的兩個字符串是不是互為變位詞。 *我們可以創建一個用數組實現的簡單哈希表，用來統計字符串中每個字符出現的次數。當掃描到第一個字符串中的每個字符時，為哈希表對應的項的值增加1。接下來掃描第二個字符串，當掃描到每個字符時，為哈希表對應的項的值減去1。如果掃描完第二個字符串后，哈希表中所有的值都是0，那么這兩個字符串就互為變位詞。* 舉一反三 如果需要判斷多個字符是不是在某個字符串里出現過或者統計多個字符在某個字符串中出現的次數，那么我們可以考慮基于數組創建一個簡單的哈希表，這樣可以用很小的空間消耗換來時間效率的提升。 Java中char與int可以這么互相轉換 int i = ch; char ch = (char) i; #### 2.2.2 字符流中第一個只出現一次的字符[?](https://blog.yorek.xyz/leetcode/code_interviews_5/#222 "Permanent link") > 請實現一個函數用來找出字符流中第一個只出現一次的字符。例如，當從字符流中只讀出前兩個字符"go"時，第一個只出現一次的字符是'g'。當從該字符流中讀出前六個字符"google"時，第一個只出現一次的字符是'l'。 字符只能一個接著一個從字符流中讀出來。可以定義一個數據容器來保存字符在字符流中的位置。當一個字符第一次從字符流中讀出來時，把它在字符流中的位置保存到數據容器里。當這個字符再次從字符流中讀出來時，那么它就不是只出現一次的字符，也就可以被忽略了。這時把它在數據容器里保存的值更新成一個特殊的值（如負數值）。 為了盡可能高效地解決這個問題，需要在O(1)時間內往數據容器里插入一個字符，以及更新一個字符對應的值。受面試題50的啟發，這個數據容器可以用哈希表來實現。用字符的ASCII碼作為哈希表的鍵值，而把字符對應的位置作為哈希表的值。實現這種思路的參考代碼如下: ~~~ // occurrence[i]: A character with ASCII value i; // occurrence[i] = -1: The character has not found; // occurrence[i] = -2: The character has been found for mutlple times // occurrence[i] >= 0: The character has been found only once private int[] occurrence; private int index; _5002() { occurrence = new int[256]; Arrays.fill(occurrence, -1); } private void insert(char ch) { int value = occurrence[ch]; if (value == -1) { occurrence[ch] = index; } else if (value >= 0) occurrence[ch] = -2; index++; } private char firstAppearingOnce() { int minIndex = Integer.MAX_VALUE; char ch = ' '; for (int i = 0; i < occurrence.length; i++) { if (occurrence[i] >= 0 && occurrence[i] < minIndex) { ch = (char) i; minIndex = occurrence[i]; } } return ch; } ~~~ 在上述代碼中，哈希表用數組occurrence實現。數組中的元素 occurrence\[i\]和ASCII碼的值為i的字符相對應。最開始的時候，數組中的所有元素都初始化為-1。當一個ASCII碼為i的字符第一次從字符流中讀出時，occurrence\[i\]的值更新為它在字符流中的位置。當這個字符再次從字符流中讀出時（occurrence\[i\]大于或等于0），occurrence\[i\]的值更新為-2。 當我們需要找出到目前為止從字符流里讀出的所有字符中第一個不重復的字符時，只需要掃描整個數組，并從中找出最小的大于等于0的值對應的字符即可。這就是函數`firstAppearingOnce`的功能。 ### 2.3 (51)數組中的逆序對[?](https://blog.yorek.xyz/leetcode/code_interviews_5/#23-51 "Permanent link") > 在數組中的兩個數字如果前面一個數字大于后面的數字，則這兩個數字組成一個逆序對。輸入一個數組，求出這個數組中的逆序對的總數。例如，在數組{7,5,6,4}中，一共存在5個逆序對，分別是(7,6)、(7,5)、(7,4)、(6,4)和(5,4)。 看到這道題目，我們的第一反應是順序掃描整個數組。每掃描到一個數字，逐個比較該數字和它后面的數字的大小。如果后面的數字比它小，則這兩個數字就組成一個逆序對。假設數組中含有n個數字。由于每個數字都要和O(n)個數字進行比較，因此這種算法的時間復雜度是O(n^2)。我們再嘗試找找更快的算法。 我們以數組{7,5,6,4}為例來分析統計逆序對的過程。每掃描到一個數字的時候，我們不能拿它和后面的每一個數字進行比較，否則時間復雜度就是O(n^2)，因此，我們可以考慮先比較兩個相鄰的數字。 如下圖(a)和(b)所示，我們先把數組分解成兩個長度為2的子數組，再把這兩個子數組分別拆分成兩個長度為1的子數組。接下來一邊合并相鄰的子數組，一邊統計逆序對的數目。在第一對長度為1的子數組{7}、{5}中，7大于5，因此(7, 5)組成一個逆序對。同樣，在第二對長度為1的子數組{6}、{4}中，也有逆序對(6,4)。由于我們已經統計了這兩對子數組內部的逆序對，因此需要把這兩對子數組排序，如圖?所示，以免在以后的統計過程中再重復統計。  統計數組{7,5,6,4}中逆序對的過程 接下來我們統計兩個長度為2的子數組之間的逆序對。我們在下圖中細分上圖(d)的合并子數組及統計逆序對的過程。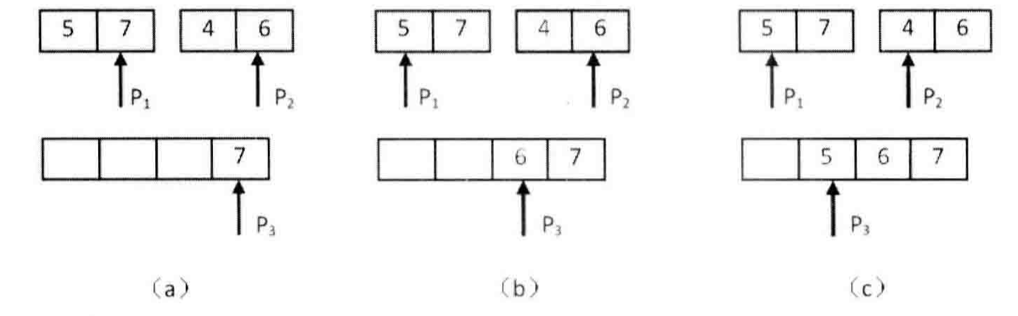  (d)的合并子數組及統計逆序對的過程 *注：圖中省略了最后一步，即復制第二個子數組最后剩余的4到輔助數組。* *a) P1指向的數字大于P2指向的數字表明數組中存在逆序對。P2指向的數字是第二個子數組的第二個數字，因此第二個子數組中有兩個數字比7小。把逆序對數目加2，并把7復制到輔助數組，向前移動P1和P3。* *b) P1指向的數字小于P2指向的數字，沒有逆序對。把P2指向的數字復制到輔助數組，并向前移動P2和P3。* *c) P1指向的數字大于P2指向的數字，因此存在逆序對。由于P2指向的數字是第二個子數組的第一個數字，子數組中只有一個數字比5小。把逆序對數目加1，并把5復制到輔助數組，向前移動P1和P3。* 我們先用兩個指針分別指向兩個子數組的末尾，并每次比較兩個指針指向的數字。如果第一個子數組中的數字大于第二個子數組中的數字，則構成逆序對，并且逆序對的數目等于第二個子數組中剩余數字的個數，如(a)和?所示。如果第一個數組中的數字小于或等于第二個數組中的數字，則不構成逆序對，如圖(b)所示。每次比較的時候，我們都把較大的數字從后往前復制到一個輔助數組，確保輔助數組中的數字是遞增排序的。在把較大的數字復制到輔助數組之后，把對應的指針向前移動一位，接下來進行下一輪比較。 經過前面詳細的討論，我們可以總結出統計逆序對的過程：先把數組分隔成子數組，統計出子數組內部的逆序對的數目，然后再統計出兩個相鄰子數組之間的逆序對的數目。在統計逆序對的過程中，還需要對數組進行排序。如果對排序算法很熟悉，那么我們不難發現這個排序的過程實際上就是歸并排序。我們可以基于歸并排序寫出如下代碼: ~~~ private int inversePairs(int[] data) { if (data == null || data.length == 0) return 0; final int n = data.length; int[] copy = new int[n]; System.arraycopy(data, 0, copy, 0, n); int count = inversePairsCore(data, copy, 0, n - 1); return count; } private int inversePairsCore(int[] data, int[] copy, int start, int end) { if (start == end) { copy[start] = data[start]; return 0; } int length = (end - start) >> 1; // copy與data每次都需要交換位置 // 使得每次遞歸后data的left、right段都是有序的 int left = inversePairsCore(copy, data, start, start + length); int right = inversePairsCore(copy, data, start + length + 1, end); // i初始化為前半段最后一個數字的下標 int i = start + length; // j初始化為后半段最后一個數字的下標 int j = end; int indexCopy = end; int count = 0; while (i >= start && j >= start + length + 1) { if (data[i] > data[j]) { copy[indexCopy--] = data[i--]; count += j - start - length; } else { copy[indexCopy--] = data[j--]; } } for (; i >= start; i--) copy[indexCopy--] = data[i]; for (; j >= start + length + 1; j--) copy[indexCopy--] = data[j]; return left + right + count; } ~~~ 我們知道，歸并排序的時間復雜度是O(nlogn)，比最直觀的O(n^2)要快，但同時歸并排序需要一個長度為n的輔助數組，相當于我們用O(n)的空間消耗換來了時間效率的提升，因此這是一種用空間換時間的算法。 ### 2.4 (52)兩個鏈表的第一個公共節點[?](https://blog.yorek.xyz/leetcode/code_interviews_5/#24-52 "Permanent link") > 輸入兩個鏈表，找出它們的第一個公共結點。 **蠻力法不可取** 在第一鏈表上順序遍歷每個節點，每遍歷到一個節點，就在第二個鏈表上順序遍歷每個節點。如果在第二個鏈表上有一個節點和第一個鏈表上的節點一樣，則說明兩個鏈表在這個節點上重合于是就找到了它們的公共節點。如果第一個鏈表的長度為m，第二個鏈表的長度為n，那么，顯然該方法的時間復雜度是O(mn)。 **使用棧** 從鏈表節點的定義可以看出，這兩個鏈表是單向鏈表。如果兩個單向鏈表有公共的節點，那么這兩個鏈表從某一節點開始，它們的next都指向同一個節點。但由于是單向鏈表的節點，每個節點只有一個next，因此從第一個公共節點開始，之后它們所有的節點都是重合的，不可能再出現分叉。所以兩個有公共節點而部分重合的鏈表，其拓撲形狀看起來像一個Y，而不可能像X，如圖所示。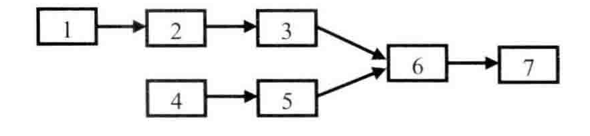  兩個鏈表在值為6的節點處交匯 經過分析我們發現，如果兩個鏈表有公共節點，那么公共節點出現在兩個鏈表的尾部。如果我們從兩個鏈表的尾部開始往前比較，那么最后一個相同的節點就是我們要找的節點。可問題是，在單向鏈表中，我們只能從頭節點開始按順序遍歷，最后才能到達尾節點。最后到達的尾節點卻要最先被比較，這聽起來是不是像“后進先出”？于是我們就能想到用棧的特點來解決這個問題：分別把兩個鏈表的節點放入兩個棧里，這樣兩個鏈表的尾節點就位于兩個棧的棧頂，接下來比較兩個棧頂的節點是否相同。如果相同，則把棧頂彈出接著比較下一個棧頂，直到找到最后一個相同的節點。 在上述思路中，我們需要用兩個輔助棧。如果鏈表的長度分別為m和n，那么空間復雜度是O(m+n)。這種思路的時間復雜度也是O(m+n)。和最開始的蠻力法相比，時間效率得到了提高，相當于用空間消耗換取了時間效率。 **推薦解法，時間復雜度為O(m+n)，不需要輔助棧** 之所以需要用到棧，是因為我們想同時遍歷到達兩個棧的尾節點。當兩個鏈表的長度不相同時，如果我們從頭開始遍歷，那么到達尾節點的時間就不一致。其實解決這個問題還有一種更簡單的辦法：首先遍歷兩個鏈表得到它們的長度，就能知道哪個鏈表比較長，以及長的鏈表比短的鏈表多幾個節點。在第二次遍歷的時候，在較長的鏈表上先走若干步，接著同時在兩個鏈表上遍歷，找到的第一個相同的節點就是它們的第一個公共節點。比如在圖的兩個鏈表中，我們可以先遍歷一次得到它們的長度分別為5和4，也就是較長的鏈表與較短的鏈表相比多一個節點。第二次先在長的鏈表上走1步，到達節點2。接下來分別從節點2和節點4出發同時遍歷兩個節點，直到找到它們第一個相同的節點6，這就是我們想要的結果。第三種思路和第二種思路相比，時間復雜度都是O(m+n)，但我們不再需要輔助棧，因此提高了空間效率。 ~~~ private ListNode findFirstCommonNode(ListNode head1, ListNode head2) { if (head1 == null || head2 == null) { return null; } // 得到兩個鏈表的長度 int m = length(head1), n = length(head2); ListNode headLong = head1, headShort = head2; // 使headLong指向長鏈表，headShort指向短鏈表 int length = Math.abs(m - n); if (m < n) { headLong = head2; headShort = head1; } // 先在長鏈表上走幾步 for (int i = 0; i < length; i++) { headLong = headLong.next; } // 再同時在兩個鏈表上遍歷 while (headLong != null && headShort != null && headLong != headShort) { headLong = headLong.next; headShort = headShort.next; } // 此時有兩種可能，一種確實是公共節點，另一種則是沒有公共節點(null) return headLong; } private int length(ListNode node) { ListNode p = node; int cnt = 0; while (p != null) { p = p.next; cnt++; } return cnt; } ~~~ 相關題目 如果把圖逆時針旋轉90°，我們就會發現兩個鏈表的拓撲形狀和一棵樹的形狀非常相似，只是這里的指針是從葉節點指向根節點的。兩個鏈表的第一個公共節點正好就是二叉樹中兩個葉節點的最低公共祖先。在后面，我們將詳細討論如何求兩個節點的最低公共祖先。