二、數據準備 · 數據科學和人工智能技術筆記

# 二、數據準備 > 作者：[Chris Albon](https://chrisalbon.com/) > > 譯者：[飛龍](https://github.com/wizardforcel) > > 協議：[CC BY-NC-SA 4.0](http://creativecommons.org/licenses/by-nc-sa/4.0/) ## 從字典加載特征 ```py from sklearn.feature_extraction import DictVectorizer staff = [{'name': 'Steve Miller', 'age': 33.}, {'name': 'Lyndon Jones', 'age': 12.}, {'name': 'Baxter Morth', 'age': 18.}] # 為我們的字典向量化器創建對象 vec = DictVectorizer() # 之后將 staff 字典轉換為向量，并輸出數組 vec.fit_transform(staff).toarray() ''' array([[ 33., 0., 0., 1.], [ 12., 0., 1., 0.], [ 18., 1., 0., 0.]]) ''' # 獲取特征名稱 vec.get_feature_names() # ['age', 'name=Baxter Morth', 'name=Lyndon Jones', 'name=Steve Miller'] ``` ## 加載 scikit-learn 的波士頓住房數據集 ```py # 加載庫 from sklearn import datasets import matplotlib.pyplot as plt ``` ## 加載波士頓住房數據集 [波士頓住房數據集](http://www.cs.toronto.edu/~delve/data/boston/bostonDetail.html) 是 20 世紀 70 年代的著名數據集。它包含506個關于波士頓周邊房價的觀測。它通常用于回歸示例，包含 15 個特征。 ```py # 加載數據集 boston = datasets.load_boston() # 創建特征矩陣 X = boston.data # 創建目標向量 y = boston.target # 查看第一個觀測的特征值 X[0] ''' array([ 6.32000000e-03, 1.80000000e+01, 2.31000000e+00, 0.00000000e+00, 5.38000000e-01, 6.57500000e+00, 6.52000000e+01, 4.09000000e+00, 1.00000000e+00, 2.96000000e+02, 1.53000000e+01, 3.96900000e+02, 4.98000000e+00]) ''' ``` 如你所見，特征未標準化。如果我們將值顯示為小數，則更容易看到： ```py # 將第一個觀測的每個特征值展示為浮點 ['{:f}'.format(x) for x in X[0]] ''' ['0.006320', '18.000000', '2.310000', '0.000000', '0.538000', '6.575000', '65.200000', '4.090000', '1.000000', '296.000000', '15.300000', '396.900000', '4.980000'] ''' ``` 因此，標準化的特征值通常是有益的和/或需要的。 ## 加載 scikit-learn 的數字數據集 ```py # 加載庫 from sklearn import datasets import matplotlib.pyplot as plt ``` 數字是手寫數字的數據集。每個特征是 8×8 圖像的一個像素的強度。 ```py # 加載數字數據集 digits = datasets.load_digits() # 創建特征矩陣 X = digits.data # 創建目標向量 y = digits.target # 查看第一個觀測的特征值 X[0] ''' array([ 0., 0., 5., 13., 9., 1., 0., 0., 0., 0., 13., 15., 10., 15., 5., 0., 0., 3., 15., 2., 0., 11., 8., 0., 0., 4., 12., 0., 0., 8., 8., 0., 0., 5., 8., 0., 0., 9., 8., 0., 0., 4., 11., 0., 1., 12., 7., 0., 0., 2., 14., 5., 10., 12., 0., 0., 0., 0., 6., 13., 10., 0., 0., 0.]) ''' ``` 觀測的特征值展示為向量。但是，通過使用`images`方法，我們可以將相同的特征值加載為矩陣，然后可視化實際的手寫字符： ```py # 將第一個觀測的特征作為矩陣查看 digits.images[0] ''' array([[ 0., 0., 5., 13., 9., 1., 0., 0.], [ 0., 0., 13., 15., 10., 15., 5., 0.], [ 0., 3., 15., 2., 0., 11., 8., 0.], [ 0., 4., 12., 0., 0., 8., 8., 0.], [ 0., 5., 8., 0., 0., 9., 8., 0.], [ 0., 4., 11., 0., 1., 12., 7., 0.], [ 0., 2., 14., 5., 10., 12., 0., 0.], [ 0., 0., 6., 13., 10., 0., 0., 0.]]) ''' # 將第一個觀測的特征作為圖像可視化 plt.gray() plt.matshow(digits.images[0]) plt.show() # <matplotlib.figure.Figure at 0x1068494a8> ``` ![png](https://chrisalbon.com/machine_learning/basics/loading_scikit-learns_digits-dataset/loading_scikit-learns_digits-dataset_7_1.png) ## 加載 scikit-learn 的鳶尾花數據集 ```py # 加載庫 from sklearn import datasets import matplotlib.pyplot as plt ``` The [Iris flower dataset](https://en.wikipedia.org/wiki/Iris_flower_data_set) is one of the most famous databases for classification. It contains three classes (i.e. three species of flowers) with 50 observations per class. ```py # 加載數字數據集 iris = datasets.load_iris() # 創建特征矩陣 X = iris.data # 創建目標向量 y = iris.target # 查看第一個觀測的特征值 X[0] # array([ 5.1, 3.5, 1.4, 0.2]) ``` ## 為分類制作模擬數據 ```py from sklearn.datasets import make_classification import pandas as pd # 創建模擬的特征矩陣和輸出向量，帶有 100 個樣本， features, output = make_classification(n_samples = 100, # 十個特征 n_features = 10, # 五個實際預測輸出分類的特征， n_informative = 5, # 五個隨機特征，和輸出分類無關， n_redundant = 5, # 三個輸出分類 n_classes = 3, # 第一類有 20% 的觀測，第二類有 30%， # 第三類有 50%，'None' 表示均衡分類。 weights = [.2, .3, .8]) # 查看前五個管澤志和它們的 10 個特征 pd.DataFrame(features).head() ``` | | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | | 0 | -1.338796 | 2.218025 | 3.333541 | 2.586772 | -2.050240 | -5.289060 | 4.364050 | 3.010074 | 3.073564 | 0.827317 | | 1 | 1.535519 | 1.964163 | -0.053789 | 0.610150 | -4.256450 | -6.044707 | 7.617702 | 4.654903 | 0.632368 | 3.234648 | | 2 | 0.249576 | -4.051890 | -4.578764 | -1.629710 | 2.188123 | 1.488968 | -1.977744 | -2.888737 | -4.957220 | 3.599833 | | 3 | 3.778789 | -4.797895 | -1.187821 | 0.724315 | 1.083952 | 0.165924 | -0.352818 | 0.615942 | -4.392519 | 1.683278 | | 4 | 0.856266 | 0.568888 | -0.520666 | -1.970701 | 0.597743 | 2.224923 | 0.065515 | 0.250906 | -1.512495 | -0.859869 | ```py # 查看前五個觀測的分類 pd.DataFrame(output).head() ``` | | 0 | | --- | --- | | 0 | 2 | | 1 | 2 | | 2 | 1 | | 3 | 2 | | 4 | 2 | ## 為矩陣生成模擬數據 ```py from sklearn.datasets import make_blobs import matplotlib.pyplot as plt # 生成特征（X）和輸出（Y），帶有 200 個樣本， X, y = make_blobs(n_samples = 200, # 兩個特征， n_features = 2, # 三個簇， centers = 3, # .5 的簇內標準差， cluster_std = 0.5, # 并打亂。 shuffle = True) # 創建前兩個特征的散點圖 plt.scatter(X[:,0], X[:,1]) # 展示散點圖 plt.show() ``` ![png](https://chrisalbon.com/machine_learning/basics/make_simulated_data_for_clustering/make_simulated_data_for_clustering_6_0.png) ## 為回歸制作模擬數據 ```py import pandas as pd from sklearn.datasets import make_regression # 生成特征，輸出和真實的相關度，樣本為 100， features, output, coef = make_regression(n_samples = 100, # 三個特征， n_features = 3, # 只有兩個特征是有用的， n_informative = 2, # 每個觀測有一個目標值， n_targets = 1, # 高斯噪聲的標準差為 0.0， noise = 0.0, # 展示用于生成數據的真實相關度。 coef = True) # 查看前五行的特征 pd.DataFrame(features, columns=['Store 1', 'Store 2', 'Store 3']).head() ``` | | Store 1 | Store 2 | Store 3 | | --- | --- | --- | --- | | 0 | -0.166697 | -0.177142 | -2.329568 | | 1 | -0.093566 | -0.544292 | 0.685165 | | 2 | 0.625958 | -0.193049 | 1.168012 | | 3 | -0.843925 | -0.567444 | -0.193631 | | 4 | -1.079227 | -0.819236 | 1.609171 | ```py # 查看前五行的輸出 pd.DataFrame(output, columns=['Sales']).head() ``` | | Sales | | --- | --- | | 0 | -149.387162 | | 1 | -4.164344 | | 2 | 52.166904 | | 3 | -56.996180 | | 4 | 27.246575 | ```py # 查看用于生成數據的真實相關度 pd.DataFrame(coef, columns=['True Coefficient Values']) ``` | | True Coefficient Values | | --- | --- | | 0 | 0.000000 | | 1 | 80.654346 | | 2 | 57.993548 | # Scikit 中的感知機感知機學習器是最早的機器學習技術之一，并且仍然是許多現代神經網絡的基礎。在本教程中，我們使用感知器學習器來分類[經典的鳶尾花數據集](https://en.wikipedia.org/wiki/Iris_flower_data_set)。這個教程受[ Sebastian Raschka 的 Python 機器學習](http://amzn.to/2iyMbpA)的啟發。 ```py # 加載所需的庫 from sklearn import datasets from sklearn.preprocessing import StandardScaler from sklearn.linear_model import Perceptron from sklearn.model_selection import train_test_split from sklearn.metrics import accuracy_score import numpy as np # 加載鳶尾花數據集 iris = datasets.load_iris() # 創建 X 和 y 數據 X = iris.data y = iris.target # 查看 y 數據的前五個觀測 y[:5] # array([0, 0, 0, 0, 0]) # 查看 x 數據的前五個觀測 # 注意有四個獨立變量（特征） X[:5] ''' array([[ 5.1, 3.5, 1.4, 0.2], [ 4.9, 3\. , 1.4, 0.2], [ 4.7, 3.2, 1.3, 0.2], [ 4.6, 3.1, 1.5, 0.2], [ 5\. , 3.6, 1.4, 0.2]]) ''' # 將數據分割為 70% 訓練集和 30% 測試集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3) # 訓練縮放器，將所有特征標準化為均值為 0 和標準差為 1。 sc = StandardScaler() sc.fit(X_train) # StandardScaler(copy=True, with_mean=True, with_std=True) # 對 X 訓練數據引用縮放器 X_train_std = sc.transform(X_train) # 對 X 測試數據應用相同的縮放器 X_test_std = sc.transform(X_test) # 創建感知機對象，參數為，40 個迭代，0.1 的學習率 ppn = Perceptron(n_iter=40, eta0=0.1, random_state=0) # 訓練感知機 ppn.fit(X_train_std, y_train) ''' Perceptron(alpha=0.0001, class_weight=None, eta0=0.1, fit_intercept=True, n_iter=40, n_jobs=1, penalty=None, random_state=0, shuffle=True, verbose=0, warm_start=False) ''' # 在 X 數據上應用已訓練的感知機，來對 y 測試數據做預測 y_pred = ppn.predict(X_test_std) # 查看預測的 y 測試數據 y_pred ''' array([0, 0, 0, 0, 0, 0, 2, 2, 0, 0, 0, 1, 1, 0, 2, 2, 2, 0, 0, 0, 0, 0, 2, 2, 1, 0, 0, 2, 1, 0, 0, 0, 0, 2, 1, 0, 2, 0, 2, 0, 2, 0, 2, 0, 1]) ''' # 查看真實的 y 測試數據 y_test ''' array([0, 0, 0, 1, 0, 0, 2, 2, 0, 0, 1, 1, 1, 0, 2, 2, 2, 1, 0, 0, 0, 0, 2, 2, 1, 1, 0, 2, 1, 1, 1, 0, 0, 2, 1, 0, 2, 0, 2, 0, 2, 0, 2, 0, 1]) ''' # 查看模型準確率，它是：1 -（預測錯的觀測 / 總觀測） print('Accuracy: %.2f' % accuracy_score(y_test, y_pred)) # Accuracy: 0.87 ``` # 保存機器學習模型在 scikit 中，有兩種方式來保存模型以便將來使用：pickle 字符串和作為文件的 pickled 模型。 ```py from sklearn.linear_model import LogisticRegression from sklearn import datasets import pickle from sklearn.externals import joblib # 加載鳶尾花數據 iris = datasets.load_iris() # 創建特征矩陣 X，和向量 y X, y = iris.data, iris.target # 訓練原始的 logistic 回歸模型 clf = LogisticRegression(random_state=0) clf.fit(X, y) ''' LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True, intercept_scaling=1, max_iter=100, multi_class='ovr', n_jobs=1, penalty='l2', random_state=0, solver='liblinear', tol=0.0001, verbose=0, warm_start=False) ''' # 將已訓練的模型保存為 pickle 字符串 saved_model = pickle.dumps(clf) # 查看 pickled 模型 saved_model # b'\x80\x03csklearn.linear_model.logistic\nLogisticRegression\nq\x00)\x81q\x01}q\x02(X\x07\x00\x00\x00penaltyq\x03X\x02\x00\x00\x00l2q\x04X\x0b\x00\x00\x00multi_classq\x05X\x03\x00\x00\x00ovrq\x06X\x08\x00\x00\x00max_iterq\x07KdX\x08\x00\x00\x00classes_q\x08cnumpy.core.multiarray\n_reconstruct\nq\tcnumpy\nndarray\nq\nK\x00\x85q\x0bC\x01bq\x0c\x87q\rRq\x0e(K\x01K\x03\x85q\x0fcnumpy\ndtype\nq\x10X\x02\x00\x00\x00i8q\x11K\x00K\x01\x87q\x12Rq\x13(K\x03X\x01\x00\x00\x00<q\x14NNNJ\xff\xff\xff\xffJ\xff\xff\xff\xffK\x00tq\x15b\x89C\x18\x00\x00\x00\x00\x00\x00\x00\x00\x01\x00\x00\x00\x00\x00\x00\x00\x02\x00\x00\x00\x00\x00\x00\x00q\x16tq\x17bX\x07\x00\x00\x00n_iter_q\x18h\th\nK\x00\x85q\x19h\x0c\x87q\x1aRq\x1b(K\x01K\x01\x85q\x1ch\x10X\x02\x00\x00\x00i4q\x1dK\x00K\x01\x87q\x1eRq\x1f(K\x03h\x14NNNJ\xff\xff\xff\xffJ\xff\xff\xff\xffK\x00tq b\x89C\x04\x07\x00\x00\x00q!tq"bX\x06\x00\x00\x00n_jobsq#K\x01X\x11\x00\x00\x00intercept_scalingq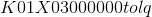![](https://img.kancloud.cn/97/18/9718eefb0a965fdc175e4adf1b0ad2ca_152x17.gif)8y\xdd\x18\x02\xc0\xac\x8f\xee\xd9+|\xe2?\\\x10\xf2\xcc\x8c\xc4\[[email?protected]](/cdn-cgi/l/email-protection)\xda\xb0;l,w\xf0\xbf8_\xe7W*+\xf6\xbf\xefT`-lq\[[email?protected]](/cdn-cgi/l/email-protection)\n\x00\x00\x00intercept_q4h\th\nK\x00\x85q5h\x0c\x87q6Rq7(K\x01K\x03\x85q8h0\x89C\x18\xd4\x86D\x03\xb1\xff\xd0?\xa2\xcc=I\xe5]\xf1?\x84\'\xad\x8dxo\xf3\xbfq9tq:bX\n\x00\x00\x00warm_startq;\x89X\x01\x00\x00\x00Cq<G?\xf0\x00\x00\x00\x00\x00\x00X\r\x00\x00\x00fit_interceptq=\x88X\x06\x00\x00\x00solverq>X\t\x00\x00\x00liblinearq?X\x0c\x00\x00\[[email?protected]](/cdn-cgi/l/email-protection)' # 加載 pickled 模型 clf_from_pickle = pickle.loads(saved_model) # 使用加載的 pickled 模型來做預測 clf_from_pickle.predict(X) ''' array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2]) ''' # 將模型作為 pickle 保存到文件 joblib.dump(clf, 'filename.pkl') ''' ['filename.pkl', 'filename.pkl_01.npy', 'filename.pkl_02.npy', 'filename.pkl_03.npy', 'filename.pkl_04.npy'] ''' # 從文件加載模型 clf_from_joblib = joblib.load('filename.pkl') # 使用加載的模型做預測 clf_from_joblib.predict(X) ''' array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2]) ''' ```