# 十一、線性回歸
> 作者:[Chris Albon](https://chrisalbon.com/)
>
> 譯者:[飛龍](https://github.com/wizardforcel)
>
> 協議:[CC BY-NC-SA 4.0](http://creativecommons.org/licenses/by-nc-sa/4.0/)
## 添加交互項

```py
# 加載庫
from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_boston
from sklearn.preprocessing import PolynomialFeatures
import warnings
# 屏蔽警告
warnings.filterwarnings(action="ignore", module="scipy", message="^internal gelsd")
# 加載只有兩個特征的數據
boston = load_boston()
X = boston.data[:,0:2]
y = boston.target
```
通過添加一個新的特征,它是交互特征的乘積,來添加交互項。
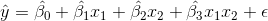
其中 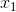 和 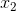 分別是兩個特征的值,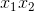 表示兩者之間的交互。使用 scikit-learn 的`PolynomialFeatures`,來為所有特征組合創建交互術項會很有用。 然后,我們可以使用模型選擇策略,來識別產生最佳模型的特征和交互項的組合。
```py
# 創建交互項(非多項式特征)
interaction = PolynomialFeatures(degree=3, include_bias=False, interaction_only=True)
X_inter = interaction.fit_transform(X)
# 創建線性回歸
regr = LinearRegression()
# 擬合線性回歸
model = regr.fit(X_inter, y)
```
## 創建交互特征
```py
# 加載庫
from sklearn.preprocessing import PolynomialFeatures
import numpy as np
# 創建特征矩陣
X = np.array([[2, 3],
[2, 3],
[2, 3]])
# 創建 PolynomialFeatures 對象,它的 interaction_only 設為 True
interaction = PolynomialFeatures(degree=2, interaction_only=True, include_bias=False)
# 轉換特征矩陣
interaction.fit_transform(X)
'''
array([[ 2., 3., 6.],
[ 2., 3., 6.],
[ 2., 3., 6.]])
'''
```
## Lasso 回歸的 Alpha 的效果
我們通常希望執行一個稱為[正則化](https://en.wikipedia.org/wiki/Regularization)的過程,其中我們會懲罰模型中的系數數量,以便僅保留最重要的系數。 當你擁有帶有 100,000 多個系數的數據集時,這一點尤為重要。
[Lasso 回歸](https://en.wikipedia.org/wiki/Lasso_(statistics))是正則化的常用建模技術。 它背后的數學非常有趣,但實際上,你需要知道的是,Lasso 回歸帶有一個參數`alpha`,而`alpha`越高,大多數特征系數越會為零。
也就是說,當`alpha`為`0`時,Lasso 回歸產生與線性回歸相同的系數。 當`alpha`非常大時,所有系數都為零。
在本教程中,我運行三個 Lasso 回歸,具有不同的`alpha`值,并顯示對系數結果的影響。
```py
from sklearn.linear_model import Lasso
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_boston
import pandas as pd
boston = load_boston()
scaler = StandardScaler()
X = scaler.fit_transform(boston["data"])
Y = boston["target"]
names = boston["feature_names"]
# 創建函數 lasso
def lasso(alphas):
'''
接受 alpha 列表。輸出數據幀,包含每個 alpha 的 Lasso 回歸的系數。
'''
# 創建空數據幀
df = pd.DataFrame()
# 創建特征名稱列
df['Feature Name'] = names
# 對于每個列表中的 alpha 值,
for alpha in alphas:
# 創建這個 alpha 值的 laaso 回歸,
lasso = Lasso(alpha=alpha)
# 擬合 lasso 回歸
lasso.fit(X, Y)
# 為這個 alpha 值創建列名稱
column_name = 'Alpha = %f' % alpha
# 創建系數列
df[column_name] = lasso.coef_
# 返回數據幀
return df
# 調用函數 lasso
lasso([.0001, .5, 10])
```
| | Feature Name | Alpha = 0.000100 | Alpha = 0.500000 | Alpha = 10.000000 |
| --- | --- | --- | --- | --- |
| 0 | CRIM | -0.920130 | -0.106977 | -0.0 |
| 1 | ZN | 1.080498 | 0.000000 | 0.0 |
| 2 | INDUS | 0.142027 | -0.000000 | -0.0 |
| 3 | CHAS | 0.682235 | 0.397399 | 0.0 |
| 4 | NOX | -2.059250 | -0.000000 | -0.0 |
| 5 | RM | 2.670814 | 2.973323 | 0.0 |
| 6 | AGE | 0.020680 | -0.000000 | -0.0 |
| 7 | DIS | -3.104070 | -0.169378 | 0.0 |
| 8 | RAD | 2.656950 | -0.000000 | -0.0 |
| 9 | TAX | -2.074110 | -0.000000 | -0.0 |
| 10 | PTRATIO | -2.061921 | -1.599574 | -0.0 |
| 11 | B | 0.856553 | 0.545715 | 0.0 |
| 12 | LSTAT | -3.748470 | -3.668884 | -0.0 |
請注意,隨著alpha值的增加,更多特征的系數為 0。
# Lasso 回歸
```py
# 加載庫
from sklearn.linear_model import Lasso
from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler
# 加載數據
boston = load_boston()
X = boston.data
y = boston.target
# 標準化特征
scaler = StandardScaler()
X_std = scaler.fit_transform(X)
```
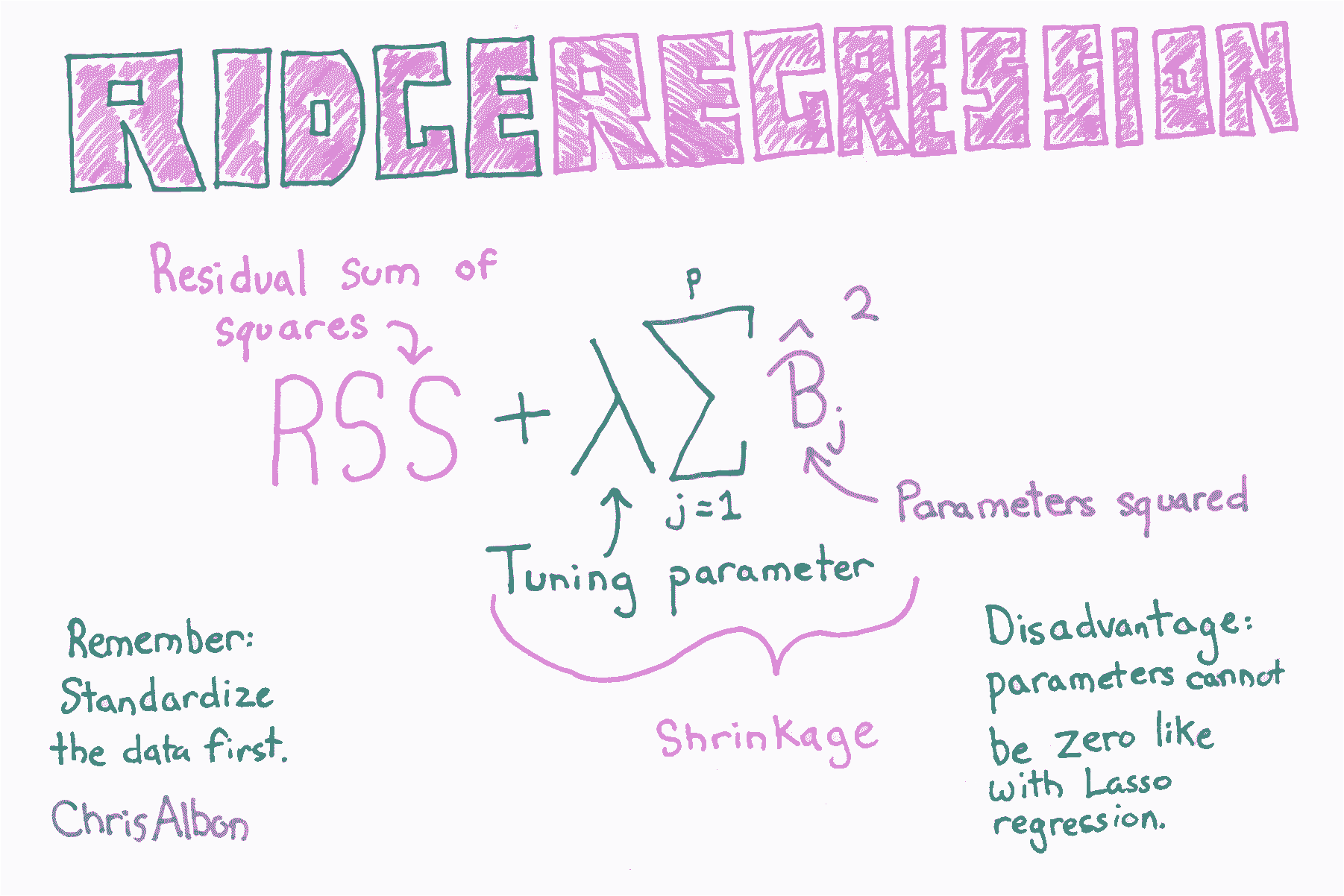
超參數  讓我們控制我們對系數的懲罰程度,更高的  值創建更簡單的模型。 的理想值應該像任何其他超參數一樣調整。 在 scikit-learn中,使用`alpha`參數設置 。
```py
# 創建帶有某個 alpha 值的 Lasso
regr = Lasso(alpha=0.5)
# 擬合 Lasso 回歸
model = regr.fit(X_std, y)
```
## 線性回歸
來源:[scikit-learn](http://scikit-learn.org/stable/auto_examples/linear_model/plot_ols.html#example-linear-model-plot-ols-py),[DrawMyData](http://robertgrantstats.co.uk/drawmydata.html).
本教程的目的是,簡要介紹機器學習中使用的統計模型構建的邏輯。如果你想更加了解本教程背后的理論,請查看[統計學習導論](https://www.amazon.com/Introduction-Statistical-Learning-Applications-Statistics/dp/1461471370)。
讓我們開始吧。
```py
import pandas as pd
from sklearn import linear_model
import random
import numpy as np
%matplotlib inline
```
添加這些庫后,讓我們加載數據集(數據集可以在他的站點的 GitHub 倉庫中找到)。
```py
# 加載數據
df = pd.read_csv('../data/simulated_data/battledeaths_n300_cor99.csv')
# 打亂數據的行(這是必要的,
# 僅僅由于我使用 DrawMyData 創建數據的方式。真正的分析中通常不需要
df = df.sample(frac=1)
```
讓我們看一下數據的前幾行,以便了解它。
```py
# 查看數據的前幾行
df.head()
```
| | friendly_battledeaths | enemy_battledeaths |
| --- | --- | --- |
| 7 | 8.2051 | 9.6154 |
| 286 | 88.7179 | 86.1538 |
| 164 | 14.3590 | 8.8462 |
| 180 | 38.9744 | 36.5385 |
| 89 | 93.0769 | 93.0769 |
現在讓我們繪制數據,以便我們可以看到它的結構。
```py
# 繪制兩個變量,彼此對照
df.plot(x='friendly_battledeaths', y='enemy_battledeaths', kind='scatter')
# <matplotlib.axes._subplots.AxesSubplot at 0x1145cdb00>
```

現在是真正的工作了。 為了判斷我們的模型有多好,我們需要一些東西來測試它。 我們可以使用稱為交叉驗證的技術來實現這一目標。 交叉驗證可以變得更加復雜和強大,但在這個例子中,我們將使用這種技術的最簡單版本。
### 步驟
1. 將數據集劃分為兩個數據集:我們將用于訓練模型的“訓練”數據集,和我們將用于判斷該模型準確率的“測試”數據集。
2. 在“訓練”數據上訓練模型。
3. 將該模型應用于測試數據的`X`變量,創建模型對測試數據`Y`的猜測。
4. 比較模型對測試數據`Y`的預測,與實際測試數據`Y`的接近程度。
```py
# 創建我們的預測器/自變量
# 以及我們的響應/因變量
X = df['friendly_battledeaths']
y = df['enemy_battledeaths']
# 從前 30 個觀測中創建測試數據
X_test = X[0:30].reshape(-1,1)
y_test = y[0:30]
# 從剩余的觀測中創建我們的訓練數據
X_train = X[30:].reshape(-1,1)
y_train = y[30:]
```
讓我們使用我們的訓練數據訓練模型。
```py
# 創建 OLS 回歸對象
ols = linear_model.LinearRegression()
# 使用訓練數據來訓練模型
model = ols.fit(X_train, y_train)
```
以下是模型的一些基本輸出,特別是系數和 R 方得分。
```py
# 查看訓練模型的系數
model.coef_
# array([ 0.97696721])
# 查看 R 方得分
model.score(X_test, y_test)
# 0.98573393818904709
```
現在我們已經使用訓練數據,來訓練一個名為`model`的模型,我們可以將它應用于測試數據的`X`,來預測測試數據的`Y`。
以前我們使用`X_train`和`y_train`來訓練線性回歸模型,我們將其存儲為一個名為`model`的變量。 代碼`model.predict(X_test)`將訓練好的模型應用于`X_test`數據,這是模型以前從未見過的數據,來生成`Y`的預測值。
只需運行代碼即可輕松看到:
```py
# 在 X_test 上運行模型并顯示前五個結果
list(model.predict(X_test)[0:5])
'''
[7.4633347104887342,
86.121700007313791,
13.475493202059415,
37.523931774900845,
90.380300060086256]
'''
```
這個數組是模型對測試數據`Y`值的最佳猜測。 將它們與實際測試數據`Y`值進行比較:
```py
# 查看前五個測試 Y 值
list(y_test)[0:5]
'''
[9.6153999999999993,
86.153800000000004,
8.8461999999999996,
36.538499999999999,
93.076899999999995]
'''
```
模型的預測值與實際值之間的差異,是我們判斷模型的準確率的方式,因為完全準確的模型沒有殘差。
但是,要判斷模型,我們需要一個可用作度量的統計量(數字)。 我們希望這個度量能夠捕獲數據中所有觀測的預測值與實際值之間的差異。
用于量化`Y`的最常見統計量是**殘差平方和**:
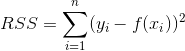
不要讓數學符號嚇到:
* 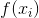 是我們訓練的模型:`model.predict(X_test)`
* 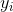 是測試數據的`y`:`y_test`
*  是指數:`**2`
* 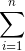 是求和:`.sum()`
在殘差的平方和中,對于每個觀測,我們找到模型的預測`Y`和實際`Y`值之間的差異,然后將該差異平方來使所有值為正。 然后我們將所有這些平方差加在一起得到一個數字。 最終結果是一個統計量,表示模型的預測與實際值的距離。
```py
# 將我們使用訓練數據創建的模型
# 應用于測試數據,并計算RSS。
((y_test - model.predict(X_test)) **2).sum()
# 313.6087355571951
```
注意:你還可以使用均方差(MSE),它是 RSS 除以自由度。 但我發現用 RSS 來思考是有幫助的。
```py
# 計算 MSE
np.mean((model.predict(X_test) - y_test) **2)
# 10.45362451857317
```
## Sklearn 線性回歸
```py
# 加載庫
from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_boston
import warnings
# 屏蔽警告
warnings.filterwarnings(action="ignore", module="scipy", message="^internal gelsd")
# 加載數據
boston = load_boston()
X = boston.data
y = boston.target
# 創建線性回歸
regr = LinearRegression()
# 擬合線性回歸
model = regr.fit(X, y)
# 查看截距(偏差)
model.intercept_
# 36.491103280361038
# 查看特征系數(權重)
model.coef_
'''
array([ -1.07170557e-01, 4.63952195e-02, 2.08602395e-02,
2.68856140e+00, -1.77957587e+01, 3.80475246e+00,
7.51061703e-04, -1.47575880e+00, 3.05655038e-01,
-1.23293463e-02, -9.53463555e-01, 9.39251272e-03,
-5.25466633e-01])
'''
```
# 嶺回歸
```py
# 加載庫
from sklearn.linear_model import Ridge
from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler
# 加載數據
boston = load_boston()
X = boston.data
y = boston.target
# 標準化特征
scaler = StandardScaler()
X_std = scaler.fit_transform(X)
```
超參數  讓我們控制我們對系數的懲罰程度,更高的  值創建更簡單的模型。 的理想值應該像任何其他超參數一樣調整。 在 scikit-learn中,使用`alpha`參數設置 。
```py
# 創建帶有 alpha 值的嶺回歸
regr = Ridge(alpha=0.5)
# 擬合嶺回歸
model = regr.fit(X_std, y)
```
# 為嶺回歸選擇最佳的 alpha 值
```py
# 加載庫
from sklearn.linear_model import RidgeCV
from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler
# 加載數據
boston = load_boston()
X = boston.data
y = boston.target
```
注意:因為在線性回歸中,系數的值由特征的尺度部分確定,并且在正則化的模型中,所有系數加在一起,我們必須確保在訓練之前將特征標準化。
```py
# 標準化特征
scaler = StandardScaler()
X_std = scaler.fit_transform(X)
# 創建帶有三個可能 alpha 值的嶺回歸
regr_cv = RidgeCV(alphas=[0.1, 1.0, 10.0])
```
scikit-learn 包含`RidgeCV`方法,允許我們為 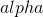 選擇理想值:
```py
# 擬合嶺回歸
model_cv = regr_cv.fit(X_std, y)
# 查看 alpha
model_cv.alpha_
# 1.0
```
