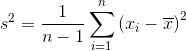
# 二十一、統計學 > 作者：[Chris Albon](https://chrisalbon.com/) > > 譯者：[飛龍](https://github.com/wizardforcel) > > 協議：[CC BY-NC-SA 4.0](http://creativecommons.org/licenses/by-nc-sa/4.0/) ## 貝塞爾校正 貝塞爾的校正是我們在樣本方差和樣本標準差的計算中使用  而不是  的原因。 樣本方差：  當我們計算樣本方差時，我們試圖估計總體方差，這是一個未知值。 為了進行這種估計，我們從樣本與總體均值的平方差的平均值，來估計未知的總體方差。 這種估計技術的負面影響是，因為我們正在采樣，我們更有可能觀察到差較小的觀測，因為它們更常見（例如它們是分布的中心）。 按照定義我們將低估總體方差。 弗里德里希貝塞爾發現，通過將有偏差（未校正）的樣本方差 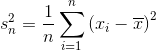 乘以 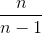，我們將能夠減少這種偏差，從而能夠準確估計總體方差和標準差。 乘法的最終結果是無偏樣本方差。 ## 演示中心極限定律 ```py # 導入包 import pandas as pd import numpy as np # 將 matplotlib 設為內聯 %matplotlib inline # 創建空的數據幀 population = pd.DataFrame() # 創建一列，它是來自均勻分布的 10000 個隨機數 population['numbers'] = np.random.uniform(0,10000,size=10000) # 繪制得分數據的直方圖 # 這確認了數據不是正態分布的 population['numbers'].hist(bins=100) # <matplotlib.axes._subplots.AxesSubplot at 0x112c72710> ```  ```py # 查看數值的均值 population['numbers'].mean() # 4983.824612472138 # 創建列表 sampled_means = [] # 執行 1000 次 for i in range(0,1000): # 從總體中隨機抽取 100 行 # 計算它們的均值，附加到 sampled_means sampled_means.append(population.sample(n=100).mean().values[0]) # 繪制 sampled_means 的直方圖 # 它很明顯是正態分布的，中心約為 5000 pd.Series(sampled_means).hist(bins=100) # <matplotlib.axes._subplots.AxesSubplot at 0x11516e668> ```  這是關鍵的圖表，記住總體分布是均勻的，然而，這個分布接近正態。 這是中心極限理論的關鍵點，也是我們可以假設樣本均值是無偏的原因。 ```py # 查看 sampled_means 的均值 pd.Series(sampled_means).mean() # 4981.465310909289 # 將樣本均值的均值減去真實的總體均值 error = population['numbers'].mean() - pd.Series(sampled_means).mean() # 打印 print('The Mean Sample Mean is only %f different the True Population mean!' % error) # The Mean Sample Mean is only 2.359302 different the True Population mean! ``` ## 皮爾遜相關系數 基于 [cbare](http://stackoverflow.com/users/199166/cbare) 的[這個](http://stackoverflow.com/a/17389980/2935984) StackOverflow 答案。 ```py import statistics as stats x = [1,2,3,4,5,6,7,8,9] y = [2,1,2,4.5,7,6.5,6,9,9.5] ``` 有許多等價的表達方式來計算皮爾遜相關系數（也稱為皮爾遜的 r）。這是一個。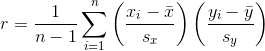  其中 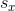 和 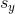 是  和  的標準差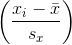， 是  和  的[標準得分](https://en.wikipedia.org/wiki/Standard_score)。 ```py # 創建函數 def pearson(x,y): # 創建 n，數據中的觀測數量 n = len(x) # 創建列表來儲存標準得分 standard_score_x = [] standard_score_y = [] # 計算 x 的均值 mean_x = stats.mean(x) # 計算 x 的標準差 standard_deviation_x = stats.stdev(x) # 計算 y 的均值 mean_y = stats.mean(y) # 計算 y 的標準差 standard_deviation_y = stats.stdev(y) # 對于 x 中的每個觀測 for observation in x: # 計算 x 的標準得分 standard_score_x.append((observation - mean_x)/standard_deviation_x) # 對于 y 中的每個觀測 for observation in y: # 計算 y 的標準得分 standard_score_y.append((observation - mean_y)/standard_deviation_y) # 將標準得分加在一起，求和，然后除以 n-1，返回該值 return (sum([i*j for i,j in zip(standard_score_x, standard_score_y)]))/(n-1) # 展示皮爾遜相關系數 pearson(x,y) # 0.9412443251336238 ``` ## 概率質量函數（PMF） ```py # 加載庫 import matplotlib.pyplot as plt # 創建一些隨機整數 data = [3,2,3,4,2,3,5,2,2,3,3,5,2,2,5,6,2,2,2,3,6,6,2,4,3,2,3] # 創建字典來儲存計數 count = {} # 對于數據中的每個值 for observation in data: # 鍵為觀測，值遞增 count[observation] = count.get(observation, 0) + 1 # 計算觀測數量 observations n = len(data) # 創建字典 probability_mass_function = {} # 對于每個唯一值 for unique_value, count in count.items(): # 將計數歸一化，通過除以數據量，添加到 PMC 字典 probability_mass_function[unique_value] = count / n # 繪制概率質量函數 plt.bar(list(probability_mass_function.keys()), probability_mass_function.values(), color='g') plt.show() ```  ## Spearman 排名相關度 ```py import numpy as np import pandas as pd import scipy.stats # 創建兩列隨機變量 x = [1,2,3,4,5,6,7,8,9] y = [2,1,2,4.5,7,6.5,6,9,9.5] ``` Spearman 的排名相關度，是變量的排名版本的皮爾遜相關系數。 ```py # 創建接受 x 和 y 的函數 def spearmans_rank_correlation(xs, ys): # 計算 x 的排名 #（也就是排序后元素的位置） xranks = pd.Series(xs).rank() # 計算 y 的排名 yranks = pd.Series(ys).rank() # 在數據的排名版本上，計算皮爾遜相關系數 return scipy.stats.pearsonr(xranks, yranks) # 運行函數 spearmans_rank_correlation(x, y)[0] # 0.90377360145618091 # 僅僅檢查我們的結果，使用 Scipy 的 Spearman scipy.stats.spearmanr(x, y)[0] # 0.90377360145618102 ``` ## T 檢驗 ```py from scipy import stats import numpy as np # 創建 20 個觀測的列表，從均值為 1， # 標準差為 1.5 的正態分布中隨機抽取 x = np.random.normal(1, 1.5, 20) # 創建 20 個觀測的列表，從均值為 0， # 標準差為 1.5 的正態分布中隨機抽取 y = np.random.normal(0, 1.5, 20) ``` ### 單樣本雙邊 T 檢驗 想象一下單樣本 T 檢驗，并繪制一個“正態形狀的”山丘，以`1`為中心，并以`1.5`為標準差而“展開”，然后在`0`處放置一個標志并查看標志在山丘上的位置。它靠近頂部嗎？ 或者遠離山丘？ 如果標志靠近山丘的底部或更遠，則 t 檢驗的 p 值將低于`0.05`。 ```py # 運行 T 檢驗來檢驗 x 的均值和 0 相比，是否有統計學顯著的差異 pvalue = stats.ttest_1samp(x, 0)[1] # 查看 p 值 pvalue # 0.00010976647757800537 ``` ### 雙樣本非配對等方差雙邊 T 檢驗 想象一下單樣本 T 檢驗，并根據標準差繪制兩個（正態形狀的）山丘，以它們的均值為中心，并根據他們的標準差繪制它們的“平坦度”（個體延展度）。 T 檢驗考察了兩座山丘重疊的程度。 它們基本上是彼此覆蓋的嗎？ 山丘的底部幾乎沒有碰到嗎？ 如果山丘的尾部剛剛重疊或根本不重疊，則 t 檢驗的 p 值將低于 0.05。 ```py stats.ttest_ind(x, y)[1] # 0.00035082056802728071 stats.ttest_ind(x, y, equal_var=False)[1] # 0.00035089238660076095 ``` ### 雙樣本配對雙邊 T 檢驗 當我們采集重復樣本，并且想要考慮我們正在測試的兩個分布是成對的這一事實時，使用配對 T 檢驗。 ```py stats.ttest_rel(x, y)[1] # 0.00034222792790150386 ``` ## 方差和標準差 ```py # 導入包 import math # 創建值的列表 data = [3,2,3,4,2,3,5,2,2,33,3,5,2,2,5,6,62,2,2,3,6,6,2,23,3,2,3] ``` 方差是衡量數據分布延展度的指標。 方差越大，數據點越“分散”。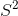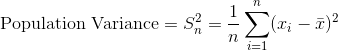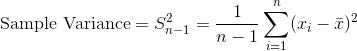 方差，通常表示為 ，計算方式如下：   其中  是觀測數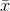， 是觀察值的平均值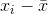， 是單個觀察值減去數據均值。 請注意，如果我們根據來自該總體的樣本估計總體的方差，我們應該使用第二個等式，將  替換為 。 ```py # 計算 n n = len(data) # 計算均值 mean = sum(data)/len(data) # 從均值創建所有觀測的差 all_deviations_from_mean_squared = [] # 對于數據中的每個觀測 for observation in data: # 計算到均值的差 deviation_from_mean = (observation - mean) # 計算平方 deviation_from_mean_squared = deviation_from_mean**2 # 將結果添加到列表 all_deviations_from_mean_squared.append(deviation_from_mean_squared) # 對于列表中所有平方差求和 sum_of_deviations_from_mean_squared = sum(all_deviations_from_mean_squared) # 除以 n population_variance = sum_of_deviations_from_mean_squared/n # 展示方差 population_variance # 160.78463648834017 ``` 標準差就是方差的平方根。 ```py # 計算總體方差的平方根 population_standard_deviation = math.sqrt(population_variance) # 打印總體標準差 population_standard_deviation # 12.68008818929664 ```