# 十五、支持向量機
> 作者:[Chris Albon](https://chrisalbon.com/)
>
> 譯者:[飛龍](https://github.com/wizardforcel)
>
> 協議:[CC BY-NC-SA 4.0](http://creativecommons.org/licenses/by-nc-sa/4.0/)
## 校準 SVC 中的預測概率
SVC 使用超平面來創建決策區域,不會自然輸出觀察是某一類成員的概率估計。 但是,我們實際上可以通過一些技巧輸出校準的類概率。 在 SVC 中,可以使用 Platt 縮放,其中首先訓練 SVC,然后訓練單獨的交叉驗證邏輯回歸來將 SVC 輸出映射到概率:
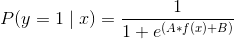
其中 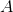 和 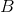 是參數向量, 是第 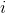 個觀測點與超平面的有符號距離。 當我們有兩個以上的類時,使用 Platt 縮放的擴展。
在 scikit-learn 中,必須在訓練模型時生成預測概率。 這可以通過將`SVC`的`probability`設置為`True`來完成。 在訓練模型之后,我們可以使用`predict_proba`輸出每個類的估計概率。
```py
# 加載庫
from sklearn.svm import SVC
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
import numpy as np
# 加載數據
iris = datasets.load_iris()
X = iris.data
y = iris.target
# 標準化特征
scaler = StandardScaler()
X_std = scaler.fit_transform(X)
# 創建支持向量分類器對象
svc = SVC(kernel='linear', probability=True, random_state=0)
# 訓練分類器
model = svc.fit(X_std, y)
# 創建新的觀測
new_observation = [[.4, .4, .4, .4]]
# 查看預測的概率
model.predict_proba(new_observation)
# array([[ 0.00588822, 0.96874828, 0.0253635 ]])
```
## 尋找最近鄰
```py
# 加載庫
from sklearn.neighbors import NearestNeighbors
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
import numpy as np
# 加載數據
iris = datasets.load_iris()
X = iris.data
y = iris.target
```
在計算任何距離之前標準化我們的數據非常重要。
```py
# 創建標準化器
standardizer = StandardScaler()
# 標準化特征
X_std = standardizer.fit_transform(X)
# 根據歐氏距離找到三個最近鄰居(包括其自身)
nn_euclidean = NearestNeighbors(n_neighbors=3, metric='euclidean').fit(X)
# 列表的列表,表示每個觀測的 3 個最近鄰
nearest_neighbors_with_self = nn_euclidean.kneighbors_graph(X).toarray()
# 刪除距離自身最近的一個觀測
for i, x in enumerate(nearest_neighbors_with_self):
x[i] = 0
# 查看第一個觀測的兩個最近鄰
nearest_neighbors_with_self[0]
'''
array([ 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0.])
'''
```
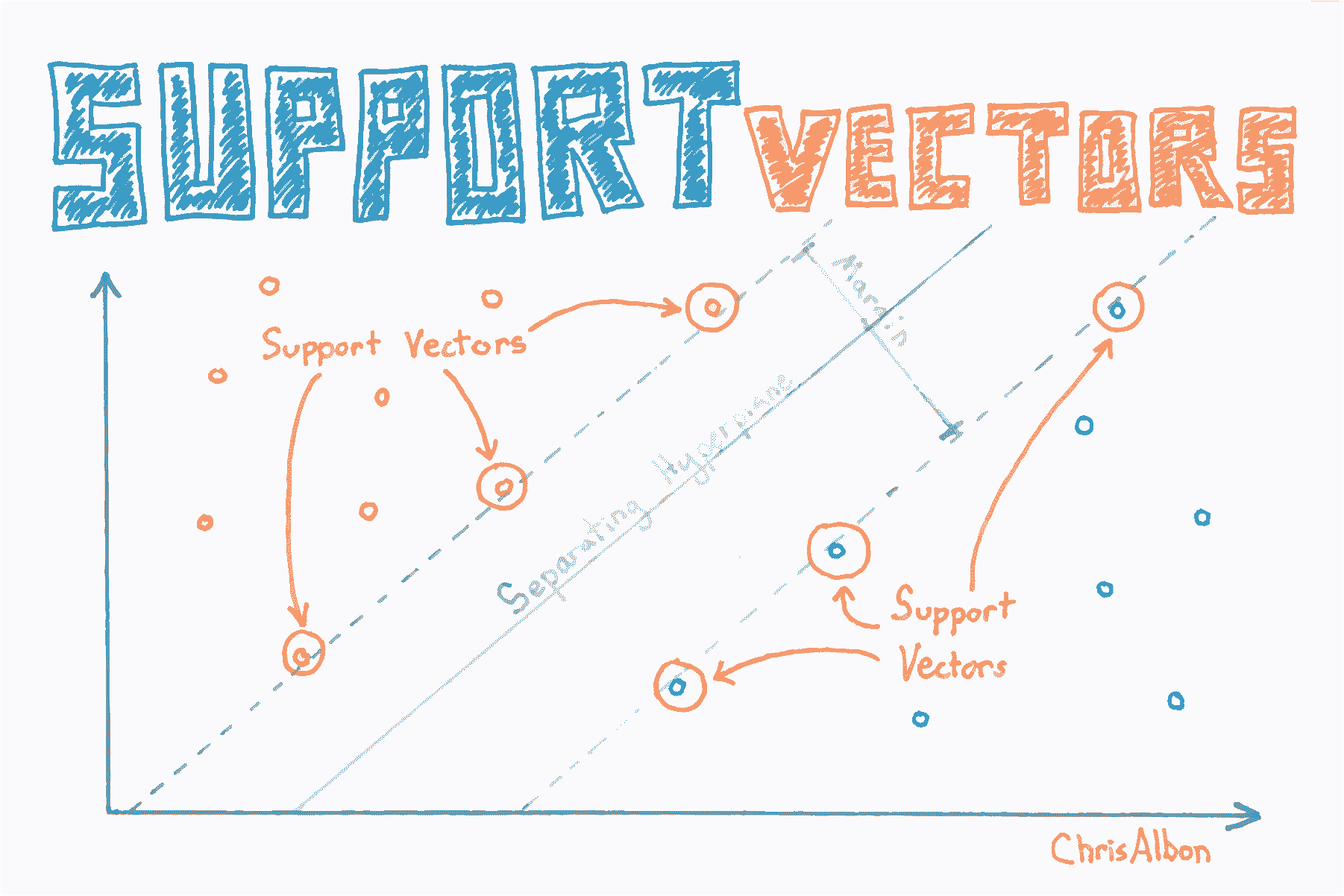
## 尋找支持向量
```py
# 加載庫
from sklearn.svm import SVC
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
import numpy as np
# 加載只有兩個分類的數據
iris = datasets.load_iris()
X = iris.data[:100,:]
y = iris.target[:100]
# 標準化特征
scaler = StandardScaler()
X_std = scaler.fit_transform(X)
# 創建支持向量對象
svc = SVC(kernel='linear', random_state=0)
# 訓練分類器
model = svc.fit(X_std, y)
# 查看支持向量
model.support_vectors_
'''
array([[-0.5810659 , 0.43490123, -0.80621461, -0.50581312],
[-1.52079513, -1.67626978, -1.08374115, -0.8607697 ],
[-0.89430898, -1.46515268, 0.30389157, 0.38157832],
[-0.5810659 , -1.25403558, 0.09574666, 0.55905661]])
'''
# 查看支持向量的下標
model.support_
# array([23, 41, 57, 98], dtype=int32)
# 查看每個分類的支持向量數
model.n_support_
# array([2, 2], dtype=int32)
```
## SVM 不平衡分類
在支持向量機中,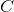 是一個超參數,用于確定對觀測的錯誤分類的懲罰。 處理支持向量機中處理不平衡類的一種方法是按類加權 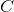。
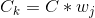
其中 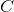 是錯誤分類的懲罰,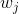 是與類 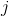 頻率成反比的權重,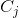 是類 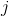 的 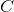 值。 一般的想法是,增加對少數類的錯誤分類的懲罰,來防止他們被多數類“淹沒”。
在 scikit-learn 中,當使用`SVC`時,我們可以通過設置`class_weight ='balanced'`來自動設置 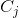 的值.`balance`參數自動對類進行加權,使得:
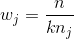
其中 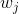 是類 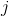 的權重, 是觀察數,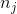 是類 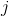 中的觀測數, 是類的總數。
```py
# 加載庫
from sklearn.svm import SVC
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
import numpy as np
# 加載只有兩個類別的數據
iris = datasets.load_iris()
X = iris.data[:100,:]
y = iris.target[:100]
# 通過刪除前 40 個觀察值使類高度不平衡
X = X[40:,:]
y = y[40:]
# 創建目標向量,表示類別是否為 0
y = np.where((y == 0), 0, 1)
# 標準化特征
scaler = StandardScaler()
X_std = scaler.fit_transform(X)
# 創建支持向量分類器
svc = SVC(kernel='linear', class_weight='balanced', C=1.0, random_state=0)
# 訓練分類器
model = svc.fit(X_std, y)
```
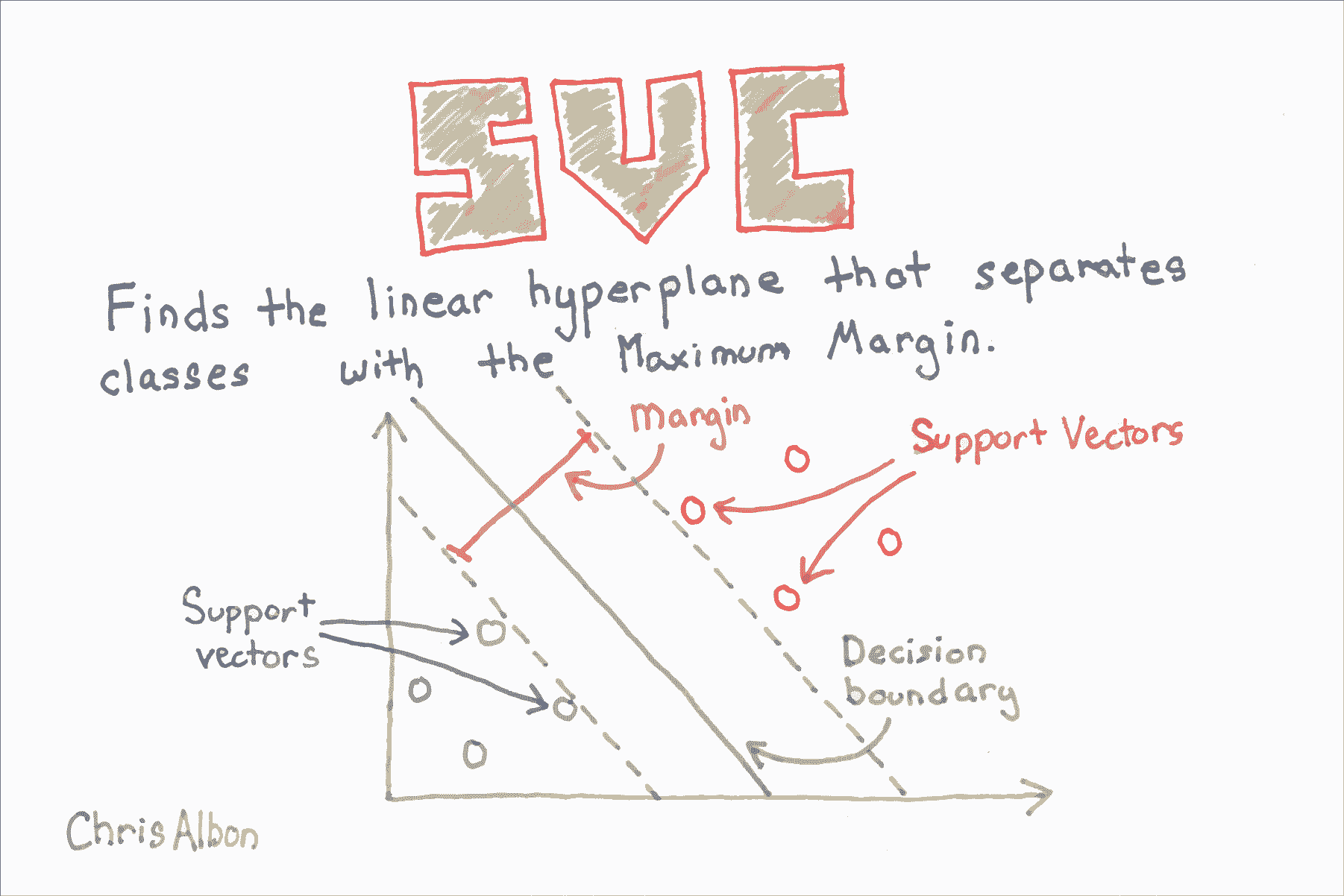
## 繪制支持向量分類器超平面
```py
# 加載庫
from sklearn.svm import LinearSVC
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
import numpy as np
from matplotlib import pyplot as plt
# 加載只有兩個分類和兩個特征數據
iris = datasets.load_iris()
X = iris.data[:100,:2]
y = iris.target[:100]
# 標準化特征
scaler = StandardScaler()
X_std = scaler.fit_transform(X)
# 創建支持向量分類器
svc = LinearSVC(C=1.0)
# 訓練模型
model = svc.fit(X_std, y)
```
在該可視化中,類 0 的所有觀測都是黑色的,類 1 的觀測是淺灰色的。 超平面是決定新觀測如何分類的決策邊界。 具體而言,直線上方的任何觀察將分為類 0,而下方的任何觀測將分為類 1。
```py
# 使用他們的類別繪制數據點和顏色
color = ['black' if c == 0 else 'lightgrey' for c in y]
plt.scatter(X_std[:,0], X_std[:,1], c=color)
# 創建超平面
w = svc.coef_[0]
a = -w[0] / w[1]
xx = np.linspace(-2.5, 2.5)
yy = a * xx - (svc.intercept_[0]) / w[1]
# 繪制超平面
plt.plot(xx, yy)
plt.axis("off"), plt.show();
```

## 使用 RBF 核時的 SVM 參數
在本教程中,我們將使用徑向基函數核(RBF)直觀地探索支持向量分類器(SVC)中兩個參數的影響。 本教程主要依據 Sebastian Raschka 的書 [Python Machine Learning](http://amzn.to/2iyMbpA) 中使用的代碼。
```py
# 導入可視化分類器的包
from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt
import warnings
# 導入執行分類的包
import numpy as np
from sklearn.svm import SVC
```
你可以忽略以下代碼。 它用于可視化分類器的決策區域。 但是,本教程中,不了解函數的工作原理并不重要。
```py
def versiontuple(v):
return tuple(map(int, (v.split("."))))
def plot_decision_regions(X, y, classifier, test_idx=None, resolution=0.02):
# 配置標記生成器和顏色表
markers = ('s', 'x', 'o', '^', 'v')
colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
cmap = ListedColormap(colors[:len(np.unique(y))])
# 繪制決策平面
x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
np.arange(x2_min, x2_max, resolution))
Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
for idx, cl in enumerate(np.unique(y)):
plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1],
alpha=0.8, c=cmap(idx),
marker=markers[idx], label=cl)
# 高亮測試樣本
if test_idx:
# plot all samples
if not versiontuple(np.__version__) >= versiontuple('1.9.0'):
X_test, y_test = X[list(test_idx), :], y[list(test_idx)]
warnings.warn('Please update to NumPy 1.9.0 or newer')
else:
X_test, y_test = X[test_idx, :], y[test_idx]
plt.scatter(X_test[:, 0],
X_test[:, 1],
c='',
alpha=1.0,
linewidths=1,
marker='o',
s=55, label='test set')
```
在這里,我們生成一些非線性可分的數據,我們將用它們訓練我們的分類器。 此數據類似于你的訓練數據集。 我們的`y`向量中有兩個類:藍色`x`和紅色方塊。
```py
np.random.seed(0)
X_xor = np.random.randn(200, 2)
y_xor = np.logical_xor(X_xor[:, 0] > 0,
X_xor[:, 1] > 0)
y_xor = np.where(y_xor, 1, -1)
plt.scatter(X_xor[y_xor == 1, 0],
X_xor[y_xor == 1, 1],
c='b', marker='x',
label='1')
plt.scatter(X_xor[y_xor == -1, 0],
X_xor[y_xor == -1, 1],
c='r',
marker='s',
label='-1')
plt.xlim([-3, 3])
plt.ylim([-3, 3])
plt.legend(loc='best')
plt.tight_layout()
plt.show()
```

使用 SVC 的最基本方法是使用線性核,這意味著決策邊界是一條直線(或更高維度的超平面)。 線性核在實踐中很少使用,但我想在此處顯示它,因為它是 SVC 的最基本版本。 如下所示,它在分類方面不是很好(從紅色區域中的所有藍色`X`,可以看出來)因為數據不是線性的。
```py
# 使用線性核創建SVC分類器
svm = SVC(kernel='linear', C=1, random_state=0)
# 訓練分類器
svm.fit(X_xor, y_xor)
# 可視化決策邊界
plot_decision_regions(X_xor, y_xor, classifier=svm)
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()
```

徑向基函數是 SVC 中常用的核:
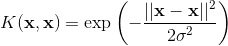
其中 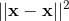 是兩個數據點 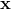 和 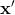 之間的歐幾里德距離的平方。 如果你不了解,塞巴斯蒂安的書有完整的描述。 但是,對于本教程,重要的是要知道,使用 RBF 核的 SVC 分類器有兩個參數:`gamma`和`C`。
### Gamma
`gamma`是 RBF 核的一個參數,可以被認為是核的“擴展”,因此也就是決策區域。 當`gamma`較低時,決策邊界的“曲線”非常低,因此決策區域非常寬。 當`gamma`較高時,決策邊界的“曲線”很高,這會在數據點周圍創建決策邊界的孤島。 我們將在下面非常清楚地看到它。
### C
`C`是 SVC 學習器的參數,是對數據點的錯誤分類的懲罰。 當`C`很小時,分類器可以使用錯誤分類的數據點(高偏差,低方差)。 當`C`很大時,分類器因錯誤分類的數據而受到嚴重懲罰,因此與之相反來避免任何錯誤分類的數據點(低偏差,高方差)。
## Gamma
在下面的四個圖表中,我們將相同的 SVC-RBF 分類器應用于相同的數據,同時保持`C`不變。 每個圖表之間的唯一區別是每次我們都會增加`gamma`的值。 通過這樣做,我們可以直觀地看到`gamma`對決策邊界的影響。
### `Gamma = 0.01`
在我們的 SVC 分類器和數據的情況下,當使用像 0.01 這樣的低`gamma`時,決策邊界不是非常“曲線”,它只是一個巨大的拱門。
```py
# 使用 RBF 核創建 SVC 分類器
svm = SVC(kernel='rbf', random_state=0, gamma=.01, C=1)
# 訓練分類器
svm.fit(X_xor, y_xor)
# 可視化決策邊界
plot_decision_regions(X_xor, y_xor, classifier=svm)
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()
```

### `Gamma = 1.0`
當我們將`gamma`增加到 1 時,你會發現很大的不同。 現在,決策邊界開始更好地覆蓋數據的延展。
```py
# 使用 RBF 核創建 SVC 分類器
svm = SVC(kernel='rbf', random_state=0, gamma=1, C=1)
# 訓練分類器
svm.fit(X_xor, y_xor)
# 可視化決策邊界
plot_decision_regions(X_xor, y_xor, classifier=svm)
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()
```

### `Gamma = 10.0`
`gamma = 10`時,核的延展不太明顯。 決策邊界開始極大地受到各個數據點(即方差)的影響。
```py
# 使用 RBF 核創建 SVC 分類器
svm = SVC(kernel='rbf', random_state=0, gamma=10, C=1)
# 訓練分類器
svm.fit(X_xor, y_xor)
# 可視化決策邊界
plot_decision_regions(X_xor, y_xor, classifier=svm)
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()
```

### `Gamma = 100.0`
對于高“伽瑪”,決策邊界幾乎完全依賴于各個數據點,從而形成“孤島”。 這些數據顯然過擬合了。
```py
# 使用 RBF 核創建 SVC 分類器
svm = SVC(kernel='rbf', random_state=0, gamma=100, C=1)
# 訓練分類器
svm.fit(X_xor, y_xor)
# 可視化決策邊界
plot_decision_regions(X_xor, y_xor, classifier=svm)
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()
```

## C - 懲罰參數
現在我們將對`C`重復這個過程:我們將使用相同的分類器,相同的數據,并保持`gamma`常量不變。 我們唯一要改變的是`C`,錯誤分類的懲罰。
### `C = 1`
使用“C = 1”,分類器明顯容忍錯誤分類的數據點。 藍色區域有許多紅點,紅色區域有藍點。
```py
# 使用 RBF 核創建 SVC 分類器
svm = SVC(kernel='rbf', random_state=0, gamma=.01, C=1)
# 訓練分類器
svm.fit(X_xor, y_xor)
# 可視化決策邊界
plot_decision_regions(X_xor, y_xor, classifier=svm)
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()
```

### `C = 10`
在`C = 10`時,分類器對錯誤分類的數據點的容忍度較低,因此決策邊界更嚴格。
```py
# 使用 RBF 核創建 SVC 分類器
svm = SVC(kernel='rbf', random_state=0, gamma=.01, C=10)
# 訓練分類器
svm.fit(X_xor, y_xor)
# 可視化決策邊界
plot_decision_regions(X_xor, y_xor, classifier=svm)
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()
```

### C = 1000
When `C = 1000`, the classifier starts to become very intolerant to misclassified data points and thus the decision boundary becomes less biased and has more variance (i.e. more dependent on the individual data points).
```py
# 使用 RBF 核創建 SVC 分類器
svm = SVC(kernel='rbf', random_state=0, gamma=.01, C=1000)
# 訓練分類器
svm.fit(X_xor, y_xor)
# 可視化決策邊界
plot_decision_regions(X_xor, y_xor, classifier=svm)
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()
```

### `C = 10000`
在`C = 10000`時,分類器“非常努力”,不會對數據點進行錯誤分類,我們會看到過擬合的跡象。
```py
# 使用 RBF 核創建 SVC 分類器
svm = SVC(kernel='rbf', random_state=0, gamma=.01, C=10000)
# 訓練分類器
svm.fit(X_xor, y_xor)
# 可視化決策邊界
plot_decision_regions(X_xor, y_xor, classifier=svm)
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()
```

### `C = 100000`
在`C = 100000`時,對于任何錯誤分類的數據點,分類器都會受到嚴重懲罰,因此邊距很小。
```py
# 使用 RBF 核創建 SVC 分類器
svm = SVC(kernel='rbf', random_state=0, gamma=.01, C=100000)
# 訓練分類器
svm.fit(X_xor, y_xor)
# 可視化決策邊界
plot_decision_regions(X_xor, y_xor, classifier=svm)
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()
```

## 支持向量分類器

SVC 在最大化超平面邊距和最小化錯誤分類之間取得平衡。 在 SVC 中,后者由超參數 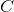 控制,對錯誤施加懲罰。`C`是 SVC 學習器的參數,是對數據點進行錯誤分類的懲罰。 當`C`很小時,分類器可以使用錯誤分類的數據點(高偏差但低方差)。 當`C`很大時,分類器因錯誤分類的數據而受到嚴重懲罰,因此向后彎曲避免任何錯誤分類的數據點(低偏差但高方差)。
在 scikit-learn 中,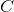 由參數`C`確定,默認為`C = 1.0`。 我們應該將 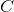 看做我們應該學習的算法的超參數,我們使用模型選擇技術調整它。
```py
# 加載庫
from sklearn.svm import LinearSVC
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
import numpy as np
# 加載特征和目標數據
iris = datasets.load_iris()
X = iris.data
y = iris.target
# 標準化特征
scaler = StandardScaler()
X_std = scaler.fit_transform(X)
# 創建支持向量分類器
svc = LinearSVC(C=1.0)
# 訓練模型
model = svc.fit(X_std, y)
# 創建新的觀測
new_observation = [[-0.7, 1.1, -1.1 , -1.7]]
# 預測新觀測的類別
svc.predict(new_observation)
# array([0])
```
