# 十二、邏輯回歸
> 作者:[Chris Albon](https://chrisalbon.com/)
>
> 譯者:[飛龍](https://github.com/wizardforcel)
>
> 協議:[CC BY-NC-SA 4.0](http://creativecommons.org/licenses/by-nc-sa/4.0/)
## C 超參數快速調優
有時,學習算法的特征使我們能夠比蠻力或隨機模型搜索方法更快地搜索最佳超參數。
scikit-learn 的`LogisticRegressionCV`方法包含一個參數`C`。 如果提供了一個列表,`C`是可供選擇的候選超參數值。 如果提供了一個整數,`C`的這么多個候選值,將從 0.0001 和 10000 之間的對數標度(`C`的合理值范圍)中提取。
```py
# 加載庫
from sklearn import linear_model, datasets
# 加載數據
iris = datasets.load_iris()
X = iris.data
y = iris.target
# 創建邏輯回歸的交叉驗證
clf = linear_model.LogisticRegressionCV(Cs=100)
# 訓練模型
clf.fit(X, y)
'''
LogisticRegressionCV(Cs=100, class_weight=None, cv=None, dual=False,
fit_intercept=True, intercept_scaling=1.0, max_iter=100,
multi_class='ovr', n_jobs=1, penalty='l2', random_state=None,
refit=True, scoring=None, solver='lbfgs', tol=0.0001, verbose=0)
'''
```
# 在邏輯回歸中處理不平衡類別
像 scikit-learn 中的許多其他學習算法一樣,`LogisticRegression`帶有處理不平衡類的內置方法。 如果我們有高度不平衡的類,并且在預處理期間沒有解決它,我們可以選擇使用`class_weight`參數來對類加權,確保我們擁有每個類的平衡組合。 具體來說,`balanced`參數會自動對類加權,與其頻率成反比:
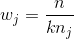
其中 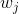 是類 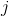 的權重, 是觀察數,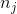 是類 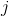 中的觀察數,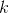 是類的總數。
```py
# 加載庫
from sklearn.linear_model import LogisticRegression
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
import numpy as np
# 加載數據
iris = datasets.load_iris()
X = iris.data
y = iris.target
# 通過移除前 40 個觀測,使類高度不均衡
X = X[40:,:]
y = y[40:]
# 創建目標向量,如果表示類別是否為 0
y = np.where((y == 0), 0, 1)
# 標準化特征
scaler = StandardScaler()
X_std = scaler.fit_transform(X)
# 創建決策樹分類器對象
clf = LogisticRegression(random_state=0, class_weight='balanced')
# 訓練模型
model = clf.fit(X_std, y)
```
## 邏輯回歸
盡管其名稱中存在“回歸”,但邏輯回歸實際上是廣泛使用的二分類器(即,目標向量只有兩個值)。 在邏輯回歸中,線性模型(例如 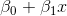)包含在 logit(也稱為 sigmoid)函數中,,滿足:
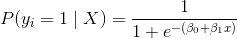
其中 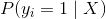 是第 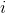 個觀測的目標值 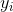 為 1 的概率, 是訓練數據, 和 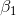 是要學習的參數, 是自然常數。
```py
# 加載庫
from sklearn.linear_model import LogisticRegression
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
# 加載只有兩個類別的數據
iris = datasets.load_iris()
X = iris.data[:100,:]
y = iris.target[:100]
# 標準化特征
scaler = StandardScaler()
X_std = scaler.fit_transform(X)
# 創建邏輯回歸對象
clf = LogisticRegression(random_state=0)
# 訓練模型
model = clf.fit(X_std, y)
# 創建新的觀測
new_observation = [[.5, .5, .5, .5]]
# 預測類別
model.predict(new_observation)
# array([1])
# 查看預測的概率
model.predict_proba(new_observation)
# array([[ 0.18823041, 0.81176959]])
```
# 大量數據上的邏輯回歸
scikit-learn 的`LogisticRegression`提供了許多用于訓練邏輯回歸的技術,稱為求解器。 大多數情況下,scikit-learn 會自動為我們選擇最佳求解器,或警告我們,你不能用求解器做一些事情。 但是,我們應該注意一個特殊情況。
雖然精確的解釋超出了本書的范圍,但隨機平均梯度下降使得我們在數據非常大時,比其他求解器更快訓練模型。 但是,對特征尺度也非常敏感,標準化我們的特征尤為重要。 我們可以通過設置`solver ='sag'`來設置我們的學習算法來使用這個求解器。
```py
# 加載庫
from sklearn.linear_model import LogisticRegression
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
# 加載數據
iris = datasets.load_iris()
X = iris.data
y = iris.target
# 標準化特征
scaler = StandardScaler()
X_std = scaler.fit_transform(X)
# 創建使用 SAG 求解器的邏輯回歸
clf = LogisticRegression(random_state=0, solver='sag')
# 訓練模型
model = clf.fit(X_std, y)
```
# 帶有 L1 正則化的邏輯回歸
L1 正則化(也稱為最小絕對誤差)是數據科學中的強大工具。 有許多教程解釋 L1 正則化,我不會在這里嘗試這樣做。 相反,本教程將展示正則化參數`C`對系數和模型精度的影響。
```py
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
```
本教程中使用的數據集是著名的[鳶尾花數據集](https://en.wikipedia.org/wiki/Iris_flower_data_set)。鳶尾花數據包含來自三種鳶尾花`y`,和四個特征變量`X`的 50 個樣本。
數據集包含三個類別(三種鳶尾),但是為了簡單起見,如果目標數據是二元的,則更容易。因此,我們將從數據中刪除最后一種鳶尾。
```py
# 加載鳶尾花數據集
iris = datasets.load_iris()
# 從特征中創建 X
X = iris.data
# 從目標中創建 y
y = iris.target
# 重新生成變量,保留所有標簽不是 2 的數據
X = X[y != 2]
y = y[y != 2]
# 查看特征
X[0:5]
'''
array([[ 5.1, 3.5, 1.4, 0.2],
[ 4.9, 3\. , 1.4, 0.2],
[ 4.7, 3.2, 1.3, 0.2],
[ 4.6, 3.1, 1.5, 0.2],
[ 5\. , 3.6, 1.4, 0.2]])
'''
# 查看目標數據
y
'''
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1])
'''
# 將數據拆分為測試和訓練集
# 將 30% 的樣本放入測試集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
```
因為正則化懲罰由系數的絕對值之和組成,所以我們需要縮放數據,使系數都基于相同的比例。
```py
# 創建縮放器對象
sc = StandardScaler()
# 將縮放器擬合訓練數據,并轉換
X_train_std = sc.fit_transform(X_train)
# 將縮放器應用于測試數據
X_test_std = sc.transform(X_test)
```
L1 的用處在于它可以將特征系數逼近 0,從而創建一種特征選擇方法。 在下面的代碼中,我們運行帶有 L1 懲罰的邏輯回歸四次,每次都減少了`C`的值。 我們應該期望隨著`C`的減少,更多的系數變為 0。
```py
C = [10, 1, .1, .001]
for c in C:
clf = LogisticRegression(penalty='l1', C=c)
clf.fit(X_train, y_train)
print('C:', c)
print('Coefficient of each feature:', clf.coef_)
print('Training accuracy:', clf.score(X_train, y_train))
print('Test accuracy:', clf.score(X_test, y_test))
print('')
'''
C: 10
Coefficient of each feature: [[-0.0855264 -3.75409972 4.40427765 0\. ]]
Training accuracy: 1.0
Test accuracy: 1.0
C: 1
Coefficient of each feature: [[ 0\. -2.28800472 2.5766469 0\. ]]
Training accuracy: 1.0
Test accuracy: 1.0
C: 0.1
Coefficient of each feature: [[ 0\. -0.82310456 0.97171847 0\. ]]
Training accuracy: 1.0
Test accuracy: 1.0
C: 0.001
Coefficient of each feature: [[ 0\. 0\. 0\. 0.]]
Training accuracy: 0.5
Test accuracy: 0.5
'''
```
注意,當`C`減小時,模型系數變小(例如,從`C = 10`時的`4.36276075`變為`C = 0.1`時的`0.0.97175097`),直到`C = 0.001`,所有系數都是零。 這是變得更加突出的,正則化懲罰的效果。
# OVR 邏輯回歸
邏輯回歸本身只是二分類器,這意味著它們無法處理具有兩個類別以上的目標向量。 但是,邏輯回歸有一些聰明的擴展來實現它。 在 One-VS-Rest(OVR)邏輯回歸中,針對每個類別訓練單獨的模型,預測觀測是否是該類(因此使其成為二分類問題)。 它假定每個分類問題(例如是不是類 0)是獨立的。
```py
# 加載庫
from sklearn.linear_model import LogisticRegression
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
# 加載數據
iris = datasets.load_iris()
X = iris.data
y = iris.target
# 標準化特征
scaler = StandardScaler()
X_std = scaler.fit_transform(X)
# 創建 OVR 邏輯回歸對象
clf = LogisticRegression(random_state=0, multi_class='ovr')
# 訓練模型
model = clf.fit(X_std, y)
# 創建新的觀測
new_observation = [[.5, .5, .5, .5]]
# 預測類別
model.predict(new_observation)
# array([2])
# 查看預測概率
model.predict_proba(new_observation)
# array([[ 0.0829087 , 0.29697265, 0.62011865]])
```
