# 十六、樸素貝葉斯 > 作者：[Chris Albon](https://chrisalbon.com/) > > 譯者：[飛龍](https://github.com/wizardforcel) > > 協議：[CC BY-NC-SA 4.0](http://creativecommons.org/licenses/by-nc-sa/4.0/) ## 伯努利樸素貝葉斯 伯努利樸素貝葉斯分類器假設我們的所有特征都是二元的，它們僅有兩個值（例如，已經是獨熱編碼的標稱分類特征）。 ```py # 加載庫 import numpy as np from sklearn.naive_bayes import BernoulliNB # 創建三個二元特征 X = np.random.randint(2, size=(100, 3)) # 創建二元目標向量 y = np.random.randint(2, size=(100, 1)).ravel() # 查看前十個觀測 X[0:10] ''' array([[1, 1, 1], [0, 1, 0], [1, 1, 1], [0, 0, 0], [1, 0, 1], [1, 1, 1], [0, 1, 1], [1, 1, 1], [1, 1, 1], [1, 1, 0]]) ''' # 創建伯努利樸素貝葉斯對象，帶有每個類別的先驗概率 clf = BernoulliNB(class_prior=[0.25, 0.5]) # 訓練模型 model = clf.fit(X, y) ``` ## 校準預測概率 類別概率是機器學習模型中常見且有用的部分。 在 scikit-learn 中，大多數學習算法允許我們使用`predict_proba`來查看成員的類別預測概率。 例如，如果我們想要僅預測某個類，如果模型預測它們是該類的概率超過 90%，則這非常有用。 然而，一些模型，包括樸素貝葉斯分類器輸出的概率，不基于現實世界。 也就是說，`predict_proba`可能預測，觀測有 0.70 的機會成為某一類，而實際情況是它是 0.10 或 0.99。 特別是在樸素貝葉斯中，雖然不同目標類別的預測概率的排名是有效的，但是原始預測概率傾向于接近 0 和 1 的極值。 為了獲得有意義的預測概率，我們需要進行所謂的校準。 在 scikit-learn 中，我們可以使用`CalibratedClassifierCV`類，使用 k-fold 交叉驗證創建校準良好的預測概率。 在`CalibratedClassifierCV`中，訓練集用于訓練模型，測試集用于校準預測概率。返回的預測概率是 k 折的平均值。 ```py # 加載庫 from sklearn import datasets from sklearn.naive_bayes import GaussianNB from sklearn.calibration import CalibratedClassifierCV # 加載數據 iris = datasets.load_iris() X = iris.data y = iris.target # 創建高斯樸素貝葉斯對象 clf = GaussianNB() # 使用 sigmoid 校準創建校準的交叉驗證 clf_sigmoid = CalibratedClassifierCV(clf, cv=2, method='sigmoid') # 校準概率 clf_sigmoid.fit(X, y) ''' CalibratedClassifierCV(base_estimator=GaussianNB(priors=None), cv=2, method='sigmoid') ''' # 創建新的觀測 new_observation = [[ 2.6, 2.6, 2.6, 0.4]] # 查看校準概率 clf_sigmoid.predict_proba(new_observation) # array([[ 0.31859969, 0.63663466, 0.04476565]]) ``` ## 高斯樸素貝葉斯分類器  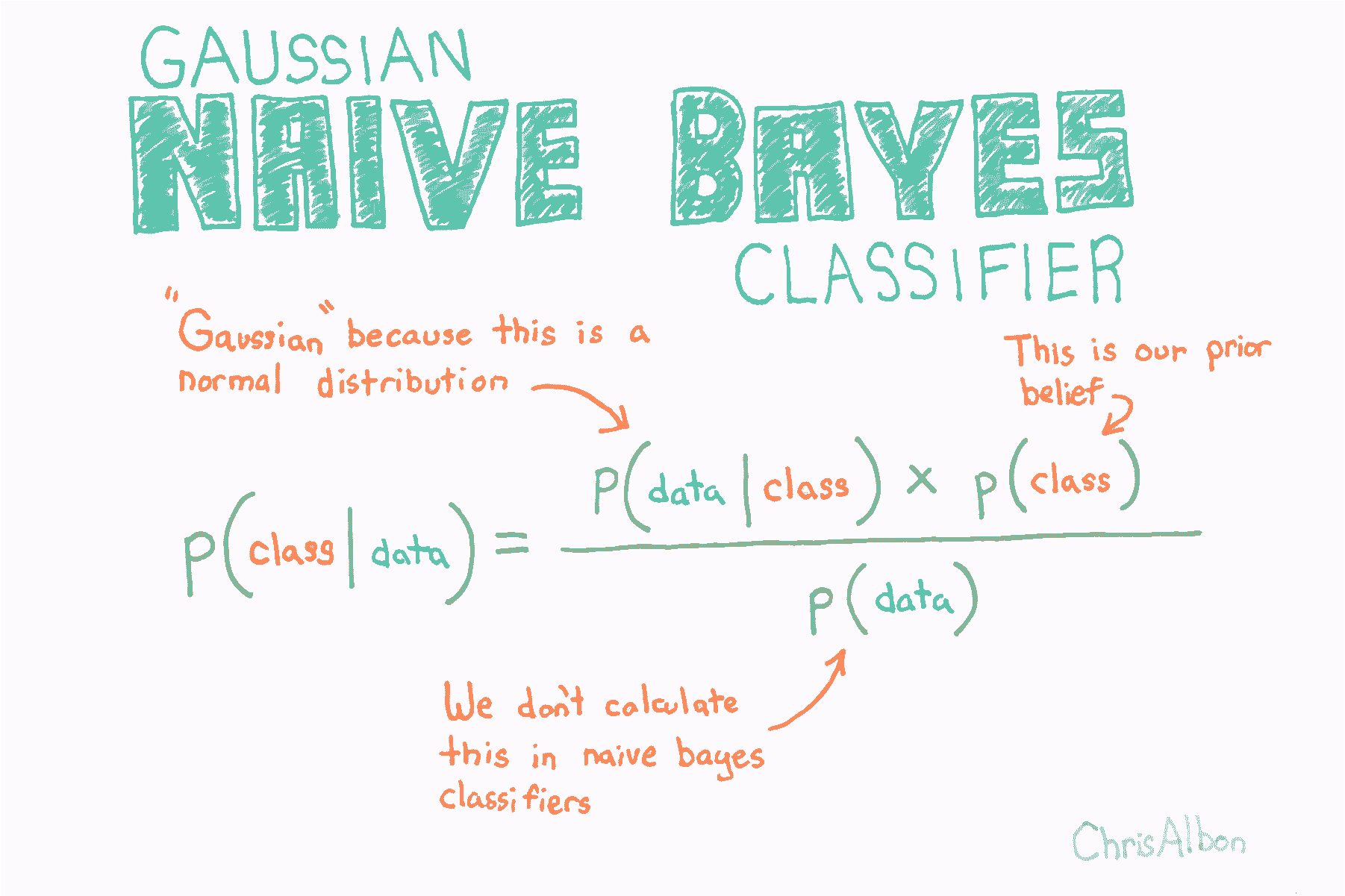由于正態分布的假設，高斯樸素貝葉斯最適用于我們所有特征都是連續的情況。 ```py # 加載庫 from sklearn import datasets from sklearn.naive_bayes import GaussianNB # 加載數據 iris = datasets.load_iris() X = iris.data y = iris.target # 創建高斯樸素貝葉斯對象，帶有每個類別的先驗概率 clf = GaussianNB(priors=[0.25, 0.25, 0.5]) # 訓練模型 model = clf.fit(X, y) # 創建新的觀測 new_observation = [[ 4, 4, 4, 0.4]] # 預測類別 model.predict(new_observation) # array([1]) ``` 注意：來自高斯樸素貝葉斯的原始預測概率（使用`predict_proba`輸出）未校準。 也就是說，他們不應該是可信的。 如果我們想要創建有用的預測概率，我們將需要使用等滲回歸或相關方法來校準它們。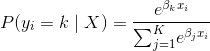 ## 多項式邏輯回歸 在多項邏輯回歸（MLR）中，我們在 Recipe 15.1 中看到的邏輯函數被 softmax 函數替換：  其中 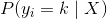 是第 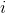 個觀測的目標值 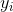 是類 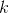 的概率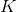， 是類的總數。MLR 的一個實際優點是使用`predict_proba`方法預測的概率更可靠（即校準更好）。 ```py # 加載庫 from sklearn.linear_model import LogisticRegression from sklearn import datasets from sklearn.preprocessing import StandardScaler # 加載數據 iris = datasets.load_iris() X = iris.data y = iris.target # 標準化特征 scaler = StandardScaler() X_std = scaler.fit_transform(X) # 創建 OVR 邏輯回歸對象 clf = LogisticRegression(random_state=0, multi_class='multinomial', solver='newton-cg') # 訓練模型 model = clf.fit(X_std, y) # 創建新的觀測 new_observation = [[.5, .5, .5, .5]] # 預測類別 model.predict(new_observation) # array([1]) # 查看預測概率 model.predict_proba(new_observation) # array([[ 0.01944996, 0.74469584, 0.2358542 ]]) ``` ## 多項式樸素貝葉斯分類器 多項式樸素貝葉斯的工作方式類似于高斯樸素貝葉斯，但假設這些特征是多項式分布的。 在實踐中，這意味著當我們具有離散數據（例如，電影評級范圍為 1 到 5）時，通常使用該分類器。 ```py # 加載庫 import numpy as np from sklearn.naive_bayes import MultinomialNB from sklearn.feature_extraction.text import CountVectorizer # 創建文本 text_data = np.array(['I love Brazil. Brazil!', 'Brazil is best', 'Germany beats both']) # 創建詞袋 count = CountVectorizer() bag_of_words = count.fit_transform(text_data) # 創建特征矩陣 X = bag_of_words.toarray() # 創建目標向量 y = np.array([0,0,1]) # 創建多項式樸素貝葉斯對象，帶有每個類別的先驗概率 clf = MultinomialNB(class_prior=[0.25, 0.5]) # 訓練模型 model = clf.fit(X, y) # 創建新的觀測 new_observation = [[0, 0, 0, 1, 0, 1, 0]] # 預測新觀測的類別 model.predict(new_observation) # array([0]) ``` ## 從零編寫樸素貝葉斯分類器 樸素貝葉斯是一種簡單的分類器，當只有少量觀測可用時，這種分類器表現良好。 在本教程中，我們將從頭開始創建一個高斯樸素貝葉斯分類器，并使用它來預測以前未見過的數據點的類別。本教程基于 Wikipedia 的[樸素貝葉斯分類器頁面](https://en.wikipedia.org/wiki/Naive_Bayes_classifier)上的示例，我已經用 Python 實現了它并調整了一些符號來改進解釋。 ```py import pandas as pd import numpy as np ``` 我們的數據集包含八個個體的數據。 我們將使用數據集構建一個分類器，該分類器接收個體的身高，體重和腳碼，并輸出其性別預測。 ```py # 創建空數據幀 data = pd.DataFrame() # 創建我們的目標變量 data['Gender'] = ['male','male','male','male','female','female','female','female'] # 創建我們的特征變量 data['Height'] = [6,5.92,5.58,5.92,5,5.5,5.42,5.75] data['Weight'] = [180,190,170,165,100,150,130,150] data['Foot_Size'] = [12,11,12,10,6,8,7,9] # 查看數據 data ``` | | Gender | Height | Weight | Foot_Size | | --- | --- | --- | --- | --- | | 0 | male | 6.00 | 180 | 12 | | 1 | male | 5.92 | 190 | 11 | | 2 | male | 5.58 | 170 | 12 | | 3 | male | 5.92 | 165 | 10 | | 4 | female | 5.00 | 100 | 6 | | 5 | female | 5.50 | 150 | 8 | | 6 | female | 5.42 | 130 | 7 | | 7 | female | 5.75 | 150 | 9 | 上面的數據集用于構造我們的分類器。 下面我們將創建一個新的個體，我們知道它的特征值，但不知道它的性別。我們的目標是預測它的性別。 ```py # 創建空數據幀 person = pd.DataFrame() # 為這一行創建相同特征值 person['Height'] = [6] person['Weight'] = [130] person['Foot_Size'] = [8] # 查看數據 person ``` | | Height | Weight | Foot_Size | | --- | --- | --- | --- | | 0 | 6 | 130 | 8 | 貝葉斯定理是一個著名的方程，它允許我們根據數據進行預測。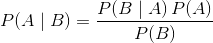 這是貝葉斯定理的經典版本：  這可能過于抽象，所以讓我們替換一些變量以使其更具體。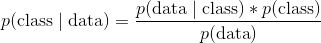 在貝葉斯分類器中，給定數據的情況下，我們有興趣找出觀測的類別（例如男性或女性，垃圾郵件或非垃圾郵件）：  其中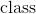： *  是特定類別（例如男性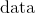） *  是觀測的數據 * 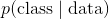 稱為后驗 * 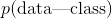 叫做似然 * 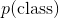 叫做先驗 * 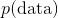 叫做邊緣概率 在貝葉斯分類器中，我們計算每個觀測的每個類的后驗（嚴格來說，我們只計算后驗的分子，但現在忽略它）。 然后，基于后驗值最大的類別對觀測分類。 在我們的例子中，我們為觀測預測兩個可能的類別（例如男性和女性），因此我們將計算兩個后驗：一個用于男性，一個用于女性。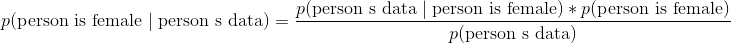   高斯樸素的貝葉斯可能是最受歡迎的貝葉斯分類器。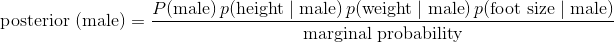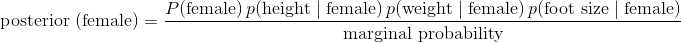 為了解釋這個名稱的含義，讓我們看一下當我們應用兩個類別（男性和女性）和三個特征變量（高度，重量和尺寸）時貝葉斯方程式的樣子：   現在讓我們解釋一下上面的方程式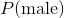： *  是先驗概率。正如你所看到的，只是觀測是男性的概率。 這只是數據集中的男性數量除以數據集中的總人數。 * 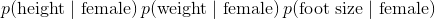 是似然。注意我們已經解釋了 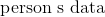 所以它現在是數據集中的每個特征。“高斯”和“樸素”來自似然中的兩個假設： 1. 如果你查看似然中的每項，你會注意到，我們假設每個特征彼此不相關。 也就是說，腳碼與體重或身高等無關。這顯然不是真的，而且是一個“樸素”的假設 - 因此稱為“樸素貝葉斯”。 2. 其次，我們假設特征的值（例如女性的身體，女性的體重）通常是高斯分布的。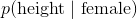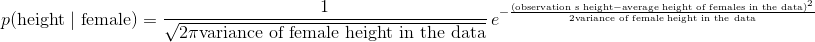這意味著  是通過將所需參數輸入正態分布的概率密度函數來計算的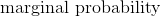：  *  可能是貝葉斯方法中最令人困惑的部分之一。 在玩具示例（包括我們的）中，完全可以計算邊際概率。 但是，在許多實際情況中，要找到邊際概率的值極其困難或不可能（解釋為什么超出了本教程的范圍）。 對于我們的分類器來說，這并不像你想象的那么嚴重。 為什么？ 因為我們不關心真正的后驗值是什么，我們只關心哪個類具有最高的后驗值。 并且因為邊際概率對于所有類別都是相同的，（1）我們可以忽略分母，（2）只計算每個類的后驗分子，（3）選擇最大的分子。 也就是說，我們可以忽略后驗分母，并僅根據后驗分子的相對值進行預測。 好的！ 理論結束。 現在讓我們開始計算貝葉斯方程的所有不同部分。 先驗可以是常數或概率分布。 在我們的例子中，這只是性別的概率。計算這很簡單： ```py # 男性數量 n_male = data['Gender'][data['Gender'] == 'male'].count() # 女性數量 n_female = data['Gender'][data['Gender'] == 'female'].count() # 總行數 total_ppl = data['Gender'].count() # 男性比例 P_male = n_male/total_ppl # 女性比例 P_female = n_female/total_ppl ``` 請記住，我們的似然中的每一項（例如 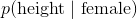）都可以看做正態的 PDF。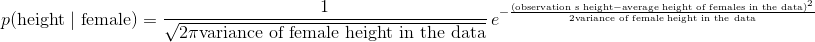 例如：  這意味著對于每個類別（例如女性）和特征（例如身高）組合，我們需要從數據計算方差和均值。Pandas 讓這很容易： ```py # 按性別分組數據，并計算每個特征的均值 data_means = data.groupby('Gender').mean() # 查看值 data_means ``` | | Height | Weight | Foot_Size | | --- | --- | --- | --- | | Gender | | | | | female | 5.4175 | 132.50 | 7.50 | | male | 5.8550 | 176.25 | 11.25 | ```py # 按性別分組數據，并計算每個特征的方差 data_variance = data.groupby('Gender').var() # 查看值 data_variance ``` | | Height | Weight | Foot_Size | | --- | --- | --- | --- | | Gender | | | | | female | 0.097225 | 558.333333 | 1.666667 | | male | 0.035033 | 122.916667 | 0.916667 | 現在我們可以創建我們需要的所有變量。 下面的代碼可能看起來很復雜，但我們所做的，只是從上面兩個表中的每個單元格中創建一個變量。 ```py # 男性的均值 male_height_mean = data_means['Height'][data_variance.index == 'male'].values[0] male_weight_mean = data_means['Weight'][data_variance.index == 'male'].values[0] male_footsize_mean = data_means['Foot_Size'][data_variance.index == 'male'].values[0] # 男性的方差 male_height_variance = data_variance['Height'][data_variance.index == 'male'].values[0] male_weight_variance = data_variance['Weight'][data_variance.index == 'male'].values[0] male_footsize_variance = data_variance['Foot_Size'][data_variance.index == 'male'].values[0] # Means for female female_height_mean = data_means['Height'][data_variance.index == 'female'].values[0] female_weight_mean = data_means['Weight'][data_variance.index == 'female'].values[0] female_footsize_mean = data_means['Foot_Size'][data_variance.index == 'female'].values[0] # Variance for female female_height_variance = data_variance['Height'][data_variance.index == 'female'].values[0] female_weight_variance = data_variance['Weight'][data_variance.index == 'female'].values[0] female_footsize_variance = data_variance['Foot_Size'][data_variance.index == 'female'].values[0] ``` 最后，我們需要創建一個函數來計算每個似然項的概率密度（例如 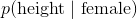）。 ```py # 創建計算 p(x | y) 的函數 def p_x_given_y(x, mean_y, variance_y): # 將參數輸入到概率密度函數 p = 1/(np.sqrt(2*np.pi*variance_y)) * np.exp((-(x-mean_y)**2)/(2*variance_y)) # 返回 p return p ``` 好的！ 我們的貝葉斯分類器準備就緒。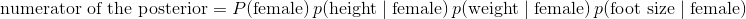 請記住，既然我們可以忽略邊際概率（分母），我們實際計算的是：  為此，我們只需要插入未分類個體（`height = 6`）的值，數據集的變量（例如女性身高的均值）和我們上面編寫的函數（`p_x_given_y`）： ```py # 如果未分類的觀測是男性的后驗分子 P_male * \ p_x_given_y(person['Height'][0], male_height_mean, male_height_variance) * \ p_x_given_y(person['Weight'][0], male_weight_mean, male_weight_variance) * \ p_x_given_y(person['Foot_Size'][0], male_footsize_mean, male_footsize_variance) # 6.1970718438780782e-09 ``` ```py # 如果未分類的觀測是女性的后驗分子 P_female * \ p_x_given_y(person['Height'][0], female_height_mean, female_height_variance) * \ p_x_given_y(person['Weight'][0], female_weight_mean, female_weight_variance) * \ p_x_given_y(person['Foot_Size'][0], female_footsize_mean, female_footsize_variance) # 0.00053779091836300176 ``` 因為女性的后驗分子大于男性，所以我們預測這個人是女性。