# (4) 策略梯度法 > 作者：[謝天](https://www.zhihu.com/people/xie-tian-55-77) > > 來源：[POST 館](https://zhuanlan.zhihu.com/c_150977189) ## 策略梯度法 在上一篇中，我們已經熟悉了智能體通過增強學習與環境打交道的運作機理：當前智能體處于某個狀態，會根據某種諸如由參數為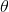的神經網絡所表示的策略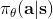，得到行動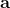，作用于環境中，由環境內在的某種動態決定的狀態轉移概率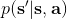得到新的狀態，接著循環往復。我們也知道了根據這樣的決策過程，由 Markov 性，一個軌跡的出現概率是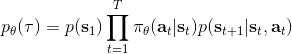。我們的目標是選出一組最優的神經網絡參數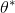最大化總收益函數的關于軌跡分布的期望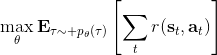。 首先我們要研究怎么去評估這個目標，然后再考慮如何去改進當前的策略。我們把目標函數記作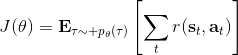。除非我們的分布性質非常干凈譬如說高斯分布，通常我們不能精確地對這個期望進行評估，但我們可以去用蒙特卡洛方法抽樣近似。如果我們根據軌跡分布來抽樣的話，目標函數的一個無偏估計是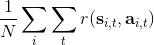，其中樣本量為，第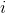個樣本在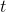時刻的狀態為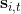，行動為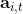。因為分布是關于我們當前策略的，因此我們抽樣的方式是在實際環境或者模擬器中運行我們的策略，來生成這些軌跡。如對于機器人，只是讓它去嘗試完成任務，看它做得怎么樣。同樣策略下，不同軌跡可能有些做得好有些做得不好，對每個軌跡得到一個評分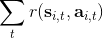，然后把這些評分平均起來來近似我們的目標函數。這是一個最簡單的利用蒙特卡洛方法來評估一個策略是否好的方式。 現在考慮怎么去改進策略，在連續優化中最常見的方法是計算其梯度，然后讓參數走一個梯度步。現在看怎么在這個目標中實現這個步驟。令軌跡的收益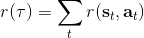，則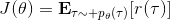。根據期望的定義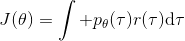，。它的梯度為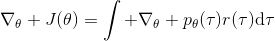，因此其實我們關心的主要是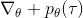這個部分。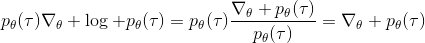以下有一個非常重要的恒等式： >  我們把這個式子代回去，得到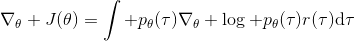，因為式子中又再度出現了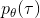這個概率，它本質上又變回了一個期望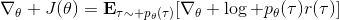：。回想我們的概率表達形式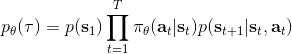，將兩邊取對數，得到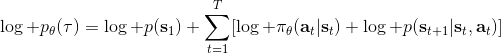。在原式子中，我們需要的是這個東西關于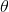的梯度，而事實上初始分布和轉移概率本身都與參數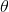并不相關。因此形式上只有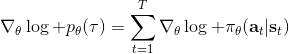。再將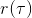展開，我們得到的最終形式如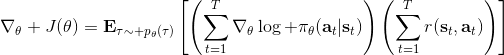。這個形式的最大優點是，它不需要我們知道狀態的初始分布，也不需要我們知道轉移概率：而這兩者通常正是非常困難的！這一點是非常重要的，我們只需要從環境中抽一些樣本來估計一個期望，然后我們唯一需要知道的事情是關于我們策略的梯度，不需要知道這個環境本身是什么樣的。 關于蒙特卡洛估計方法，與之前類似，我們也可以從實際系統中抽樣，用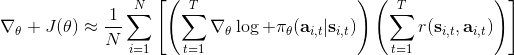來作為一個無偏估計。得到梯度后，使用梯度上升法走一個的梯度步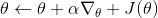。我們在上一篇提到過一般的增強學習算法都可以由三大塊構成，第一步橙色方塊是我們生成很多樣本，用于估計目標函數和梯度；第二步綠色方塊用來估計收益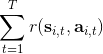，用于判斷我們的策略有多好，非常簡單，只需要一個加總；第三步藍色方塊需要我們搞清楚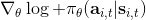，求出梯度然后走一個梯度步。這樣，我們就得到了一個最簡單的策略梯度法 REINFORCE (Williams, 1992)： 1. 運行策略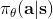，抽取樣本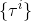； 2. 估計梯度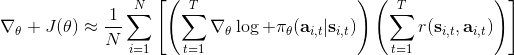； 3. 走一個梯度上升步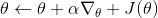。 不幸的是，通常直接這么做效果不會很好，因此我們需要做很多工作讓它能真正運行起來。但在優化這個算法之前，我們首先要解決之前的遺留問題，搞清楚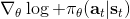到底是什么。這個是根據策略分布不同而有差異的，譬如說之前我們所講述的模仿學習之中，模仿學習也想學習一個策略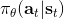，從一個狀態輸出一個行動之類：假設我們只有兩種操作，向左轉或者向右轉，那么策略就變成了一個向左或者向右的概率。 考慮一個人形機器人的控制問題。此時小人需要得到連續的控制變量，而不是離散的。假設我們的策略函數輸出的是一個高斯分布，形如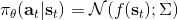，我們的神經網絡根據當前狀態輸出均值，而一個簡單的情形，協方差矩陣可能是固定的。根據分布函數，我們有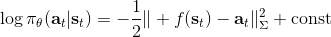，形式非常簡單；將它取梯度，得到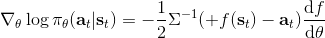。在實踐中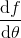，是對神經網絡取梯度，需要一次反向傳播。而訓練神經網絡我們也是走一個梯度步，因此我們只需要在走梯度步的時候乘上權重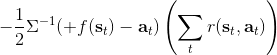就行。 我們回顧一下之前我們都做了些什么。我們用軌跡樣本近似了目標函數的梯度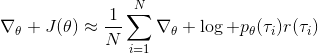。在普通的監督學習之中，我們可能會嘗試使用極大似然估計，梯度是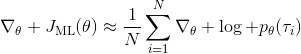。可以發現策略梯度在做非常相似的事情，除了策略梯度法嘗試對不同的樣本進行加權，權重是收益函數之和。每個樣本的收益可正可負，因此在行為上，極大似然估計梯度總是嘗試去增加所有樣本的出現概率，而策略梯度法則嘗試去減少一些不好的樣本的出現概率，增加其他樣本的出現概率，屬于一個趨利避害的試錯過程的梯度上升法版本。在計算機程序上，這兩者也是非常相似的：如果我們能有代碼計算極大似然估計，那么它也可以稍作修改以執行策略梯度法。 如果我們的觀測不完全，即只有部分觀測信息，怎么辦？在策略梯度法中，這不是個問題。我們可以得到基于觀測的梯度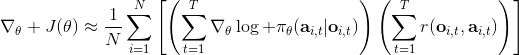，可以發現這個式子中完全沒有用到 Markov 性。也就是說，我們可以直接在 POMDP 中使用策略梯度法，不需要任何的修改；但是在之后的諸如演員-評論家算法、Q 學習算法之類的，這個性質往往是不成立的。這是策略梯度法的一大優勢。但即便如此，它不能保證你能得到一個運行得很好的策略，因為非 Markov 性可能導致真正運行得好的策略和之前的歷史有關，但是它能在你的**策略簇中**找到一個不錯的策略。如果你覺得歷史還是非常重要的，那么可能使用一個 RNN 會好一些。 策略梯度法通常會有一些問題。第一個問題下一節會講，第二個問題我們會在將來討論怎么去緩解。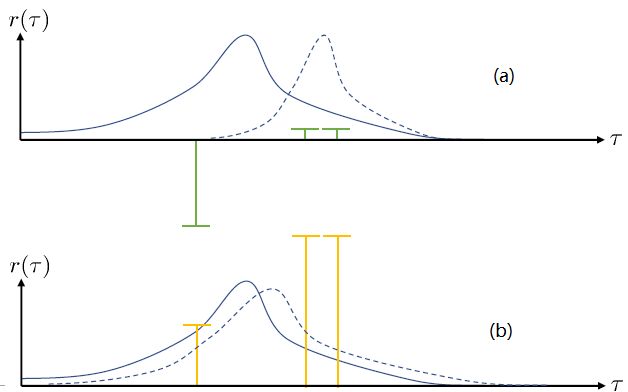  第一個問題：在兩個圖中，x 軸代表軌跡，而 y 軸代表軌跡對應的收益。藍色實線是我們選取策略的分布密度。我們從分布之中抽取了三個樣本，在(a)圖中，可以發現最左邊的樣本的收益是一個很大的負數，而右邊兩個都是很小的正數。我們想做的就是把我們的策略右移到右邊的虛線，使得在壞的位置密度更低，好的位置密度更高。實際上，正負的數值對這個算法影響很大：兩個小正數和一個大負數可能把步伐拉得比較大。而我們(b)圖中，只是把收益都加上了一個很大的常數，收益之間的相對差不變。如果我們**把所有情況的收益都增減同一個常數**，我們可以把這個常數從這個期望中提出來，作為一個與參數無關的部分，因此**整個期望關于參數求梯度的結果是不發生變化的**。此時，策略梯度法就會想增加第一個樣本的概率（行為發生了根本性變化），但更想增加后兩個的概率。這個情況下，移動的步伐就小了很多，取而代之的是可能方差就增大了，變得更平緩了。這一點被稱為“**高方差**”問題。一個更極端的情形是，有很好的樣本，但是它的收益函數是 0（其他的樣本收益為負數），那么如何動完全依賴于我現在的策略在什么位置。我們只需要把獎勵函數整體上下移動，就可以完全改變策略梯度法的行為。這個問題主要是因為如果我們選取無數個樣本的話，那么這些差異互相會被抵消掉；但是對有限個樣本的選擇會很有偏差，就會導致這樣的問題：對于這樣的高方差問題，當然增加樣本總是能緩解的，但是增加樣本也使得學習效率降低。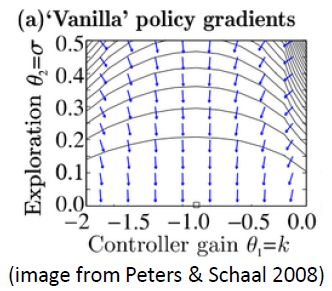  第二個問題：讓我們考慮一個一維的連續狀態和行動的增強學習問題。參數是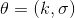。對數策略函數是一個高斯分布，由這兩個參數確定，整個簇的形式是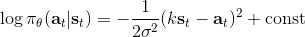，依賴于行動和均值之差的平方，其中均值是當前狀態的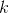倍。收益函數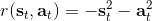，前一部分表明最終狀態希望是 0，后一部分說明我們希望行動大小盡量小：這在機械中是很合理的，如果我們的行動是電動機指令的話，通常不希望讓電動機運轉過強。在最優控制領域，這是一個 LQR 問題，可以用解析方法求出最優解，也很容易分析。但是在策略梯度法中，有趣的是，因為收益函數希望行動盡量小，梯度法總會傾向于減小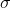（見上圖，藍色箭頭為梯度，總在降低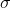的方向），用于減少很大的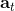的概率：因為概率來源于高斯分布，而高斯分布的支撐集非常大。事實上，更小的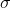，更傾向于讓我們進一步減少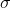。即便我們的梯度總是指向正確的方向，它在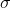上的分量更長些：在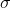很小時候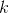，分量的大小可以忽略不計了。因此一個結果是，我們會快速下降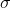，然而逐漸地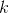就不動了，所以最終得到一個正確結果的速度奇慢無比。這也導致了策略梯度法的收斂速度很慢，而且選擇學習率也是一個很難的問題：如果因為收斂速度慢而使用了較大的步長，反而更快地進入了一個讓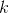難以動彈的狀況。 ## 方差削減 第一種方法是使用**因果關系** (casuality)。回顧我們的梯度為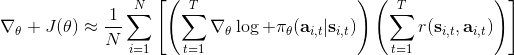。因果關系指的是，在時間點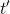的策略不能影響時間點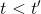的收益。這個關系看起來很蠢，就像今天做的事情不會影響昨天已經發生的事情。而事實上我們可以用這個關系得到更好的估計量。我們把后者這個括號做進前面去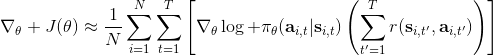，。從另一個角度看，我們根據概率的可加性有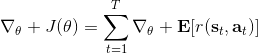 ，其中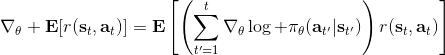，相當于是一個在當前時點截斷的軌跡，因為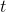時刻的收益的概率分布之和之前有關而與之后無關。我們將雙重求和號調整順序，得到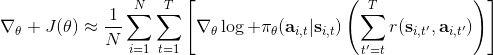：正好是我們之前論述的，一個策略只影響從它之后的部分。我們把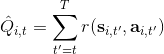記作今后收益 (reward-to-go)，也就是從這個時刻起的收益。這樣做的一大好處就是，我們這樣采樣做，數值求和上減少了，方差也傾向于隨之減少；更重要的是我們幾乎沒有理由不這么做，這么做基本上總是好的，即便是計算上實現起來稍微復雜了一點，但也只是一個從后往前加的后綴和的事情。 第二種有效的方法是**基準線** (baseline)。回到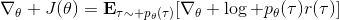，我們希望好的軌跡的收益函數是正的，而差的軌跡是負的。然而之前也提到了它對值非常敏感，如果收益函數增加或者減少一個常數，結果就會很不同。所以我們想做的，可能是不依賴于軌跡自身有多好，而是一條軌跡**比平均好多少**：這里的平均指的是我們平時通常情況的普遍收益。舉個例子，平均可以是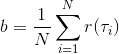，然后我們使用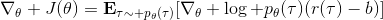。看起來是非常合理的，而且更重要的是在這里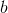是某個常數的話，這樣做總是對的。數學上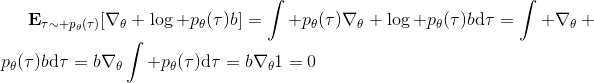， 。其中第一個等號是把期望寫成積分形式，第二個等號直接利用了我們之前的恒等關系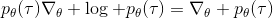，第三個利用了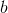是常數和積分微分可交換的性質，第四個利用了對一個概率密度積分恒等于 1 的性質。因此我們減去一個常數的基準線，這樣得到的估計總是在期望意義下無偏的。 當然，我們這么取平均得到一個基線常數不見得是最好的，但是實際效果卻通常較好。為了降低方差，我們可以求出一個理論上最優的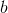。回憶方差的表達式為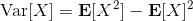。而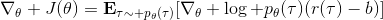，其方差為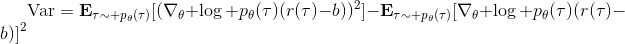：  ，而我們在前面已經證明了后面一塊等價于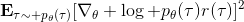，與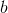是不相關的。我們將方差取微商取一階最優性條件，令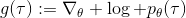，得到 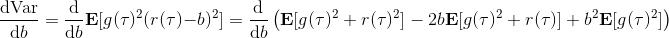 ，其中第一項微分后為 0。要使該微商等于 0，則需要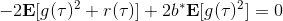，因此最優解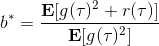。本質上來說，它是一個關于概率梯度的加權平均，不同樣本的權重不同是因為概率的梯度不同。而我們前面說的簡單平均只是它的一個粗糙簡化版本而已，也是有一些理論根據的。在實踐中也沒有發現很大的效果差異。 ## 離線的策略梯度法 我們不難發現策略梯度法是一個在線 (on-policy) 算法，這是因為策略梯度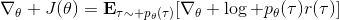，求期望的時候必須是從當前的分布上采樣才能有無偏性，而這就要求每次梯度更新之后就根據新分布全部重新采樣：如果策略是一個非常復雜的神經網絡，每次迭代可能只更新一點點，但也要求把之前的樣本全都扔了然后重新采樣，對數據的利用率是非常低的。在前面也提到了，使用策略梯度法選擇學習率可能是很難的，收斂速度也可以非常低。 如果我們沒有從最新的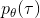中得到的樣本呢？雖然我們還是要求去估計期望，但是我們可以考慮用其他分布去估計它。假設我們有一堆從分布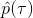中抽取出來的數據，并知道對應的軌跡和收益，那我們就可以使用**重要性抽樣** (importance sampling) 的方法。 > 重要性抽樣的原理是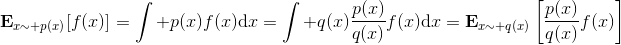 ，給了我們用其他分布的數據進行無偏估計的方法，但前面需要乘上一塊東西，算是重新加個權重。 換到我們的目標函數上，則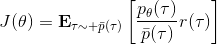。這里我們需要具體分析這個權重是什么。由于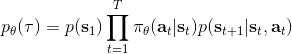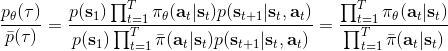， ，同樣最難處理的初始分布和轉移概率也被消掉了：我們依然保持了無需知道這些繁瑣內容的性質。在實踐上可能會有一些問題，但是至少在理論上還是無偏的：只要給定足夠多的樣本就行。 現在我們要求出目標函數的梯度了。使用重要性抽樣的技術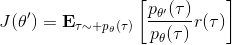，，可以發現與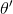有關的部分僅僅是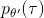，因此將目標函數求梯度得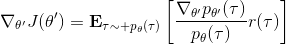。繼續利用恒等式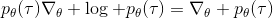，得到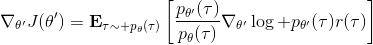。我們將其展開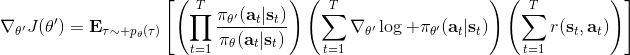， 這個和之前還是比較相似的，只是前面加了一塊權重。同樣，之前所說的因果關系可以加到這里來，類似的推導過程可以得到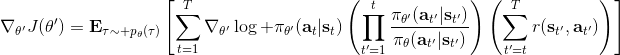 ，可以理解為概率這塊到此時為止，而收益從此時開始看起。 那么這么做的問題主要在哪里呢？我們不難看出中間這塊連乘部分的數值，是關于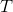指數增長的，如果每個數都略小于 1，而時間軸非常長，這個乘積最終將非常接近于 0，這樣梯度效果就會很差了。 在課程的后面會具體介紹怎么解決，而這里給一個預覽。我們把目標函數重寫為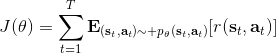，寫成一個邊際分布下的期望求和的形式。根據我們的決策過程，把期望進一步展開成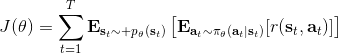。 這樣，我們就可以在兩個層面上做重要性抽樣了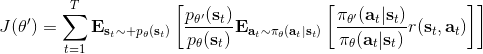：。這樣就不再有指數乘積問題，但是同時又帶來了一個新的需要知道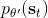這樣給定策略下某個時刻在某個狀態的概率這樣的大難題。一個近似的處理方式是我們可以把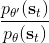這塊弄掉，當然這樣做的話理論上就不再無偏了，但是事實上當兩個策略足夠接近的話，可以說明這個比值是不重要的：在很多問題的實踐上是好的，而且有一定的理論保證。 ## 用自動差分器做策略梯度法 我們現在想找到一個比較簡單的方法去實現策略梯度法，以利用上 TensorFlow 或者 PyTorch 等自動差分器。回顧梯度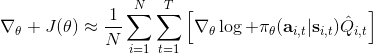，我們不想顯式地去計算這些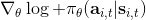，然后再做乘法丟回去。我們需要一個圖結構，可以用監督學習，它的極大似然的梯度正好是我們的策略梯度，那樣就完美解決了。考慮到極大似然估計的目標函數為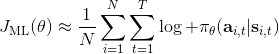，梯度為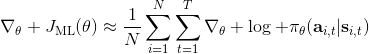。我們要把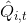給放進去。一個特性是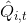，本身是不依賴于參數的，我們所需要做的一切就是做一個虛擬的損失函數，加權損失函數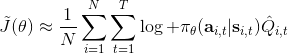，其中權重就是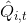，然后就用自動差分器求梯度就行了。當然，在線方法要求我們每一個梯度步重新采樣，所以我們不能使用 SGD。 Levine 教授給出了 TensorFlow 樣式的代碼例子，給出了兩者的區別（狀態和行動認為是離散的，所以是 one-hot 編碼，因此輸入是二維張量）： **最大似然估計：** ``` # Given: # actions -(N*T) x Da tensor of actions # states -(N*T) x Ds tensor of states # Build the graph: logits = policy.predictions(states) # This should return (N*T) x Da tensor of action logits negative_likelihoods = tf.nn.softmax_cross_entropy_with_logits(labels=actions, logits=logits) loss = tf.reduce_mean(negative_likelihoods) gradients = loss.gradients(loss, variables) ``` **策略梯度法：** ``` # Given: # actions -(N*T) x Da tensor of actions # states -(N*T) x Ds tensor of states # q_values – (N*T) x 1 tensor of estimated state-action values # Build the graph: logits = policy.predictions(states) # This should return (N*T) x Da tensor of action logits negative_likelihoods = tf.nn.softmax_cross_entropy_with_logits(labels=actions, logits=logits) weighted_negative_likelihoods = tf.multiply(negative_likelihoods, q_values) loss = tf.reduce_mean(weighted_negative_likelihoods) gradients = loss.gradients(loss, variables) ``` 可以發現差別還是很小的，只是加了一個加權的過程。 在實踐中，我們需要記住梯度的方差是非常大的，處理監督學習的方法不見得在這里適用，而且噪音非常大。一個比較實際的解決方法是使用很大的批量數據來降低方差。調整學習率是很有挑戰性的，而且可能會需要很多時間來做這件事情。使用自適應的步長如 ADAM 等方法通常還可以。在之后的課程中會講一些針對策略梯度法的步長調整方法。 Levine and Koltun (2013) 訓練模擬機器人，使用重要性抽樣的方法用演示例子去訓練神經網絡代表的策略。一點啟發是抽樣的分布不見得一定要是一個神經網絡分布，也可以是其他給定數據的分布：這樣如果那個分布好的話，可以減少訓練所需要的時間，可以說是一個熱啟動。Schulman et al. (2015) 使用信賴域策略優化算法 (TRPO) 訓練模擬機器人，使用自然梯度，并使用了自動調節步長的方法，可以做出離散和連續的行動，也可以玩 Atari 游戲。可以找到相關代碼 (Duan et al., 2016, [https://arxiv.org/abs/1604.06778](https://link.zhihu.com/?target=https%3A//arxiv.org/abs/1604.06778), [rll/rllab](https://link.zhihu.com/?target=https%3A//github.com/rll/rllab))。這個方法適用范圍比較廣，如果不關注樣本效率的話，通常較容易用于新的問題。